基于速度距离网络的列车运行曲线优化

引用本文

王义惠, 朱松巍, 刘硕, 于柯, 宿帅. 基于速度距离网络的列车运行曲线优化[J]. 北京交通大学学报, 2020,44(2): 36-43.
WANG Yihui, ZHU Songwei, LIU Shuo, YU Ke, SU Shuai. Train trajectory optimization based on a speed-distance network[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2020,44(2): 36-43.
Doi:10.11860/j.issn.1673-0291.20190064 复制到剪切板

Permissions

北京交通大学学报编辑部所有

基于速度距离网络的列车运行曲线优化

王义惠¹, 朱松巍¹, 刘硕², 于柯², 宿帅¹

1.北京交通大学轨道交通控制与安全国家重点实验室,北京 100044

2.北京市地铁运营有限公司,北京 100044

第一作者:王义惠(1987—),女,云南会泽人,副教授,博士.研究方向为轨道交通自动化与控制.email:yihui.wang@bjtu.edu.cn.

收稿日期: 2019-11-12

基金: 国家自然科学基金(61503020); 北京市地铁运营有限公司地铁运营技术研发中心项目(I19L00060)

摘要

轨道交通的节能研究在环保与经济方面具有重要的意义.以最小化单列车运行过程中产生的能耗为目标,基于列车的非线性动力学模型构建离散的速度距离网络,将列车运行曲线优化问题转化为一个整数规划问题,采用拉格朗日松弛和最短路径算法优化列车运行曲线.在此基础上,提出在粗粒度网络最优解的小邻域内重构细粒度的速度距离网络的方法,可有效提高运算速度.基于北京地铁亦庄线的线路和车辆数据,设计仿真案例对上述算法进行评估,并与遗传算法、基于CPLEX的整数规划算法和混合整数规划算法的求解效果进行对比.结果表明:提出的基于速度距离网络的求解算法可生成能耗更优且误差较小的列车速度曲线,并精准满足运行时间与终点速度约束.

关键词: 交通信息工程及控制; 城市轨道交通; 列车运行曲线; 速度距离网络; 拉格朗日松弛

中图分类号:U268.43 文献标志码:A 文章编号:1673-0291(2020)02-0036-08

Train trajectory optimization based on a speed-distance network

WANG Yihui¹, ZHU Songwei¹, LIU Shuo², YU Ke², SU Shuai¹

1. State Key Lab of Rail Traffic Control Safety, Beijing Jiaotong University, Beijing 100044, China

2. Beijing Subway Operation Co., Ltd., Beijing 100044, China

Fund:National Nature Science Foundation of China(61503020); Project of Subway Operation Technology R&D Center of Beijing Subway Operation Co.Ltd.(I19L00060)

Abstract

The research on energy-efficiency in rail transit systems is of great significance in environmental protection and economy. To minimize operational energy consumption, a nonlinear dynamic model for the train’s operation is presented to build a discrete speed-distance network. The optimization problem is formulated as a integer linear problem, which is solved by Lagrangian Relaxation (LR) and the shortest path algorithm. On this basis, a method of reconstructing a fine-grained network in the neighborhood of a coarse-grained network’s solution is adopted, which improves the operation speed effectively. Based on the line and vehicle data of Beijing Metro Yizhuang Line, a simulation case is designed to evaluate the above optimization algorithm, compared with the genetic algorithm, the integer linear programming and mixed integer linear programming algorithm based on CPLEX. The results show that the speed-distance network has less energy consumption and error, which contributes to satisfing the end time and the end speed constraints precisely.

Keyword: traffic information engineering and control; urban rail transit; train speed trajectory; speed-distance network; Lagrangian relaxation

文章图片

轨道交通具有高速、节能、环保、可靠性高的优点, 适应城市发展的需要, 能够有效缓解交通压力、促进经济的发展.列车自动运行系统使列车操作自动化, 能有效降低司机劳动强度、提高乘客舒适度、提升运输效率.而最优化速度距离运行曲线是列车自动运行(Automatic Train Operation, ATO)系统的基础之一^[1], 在节能方面发挥着重要的作用.

自1968年Ichikawa^[2]首次采用最大值原理对列车运行曲线优化以来, 研究学者对列车运行曲线优化展开了广泛而深入的研究.列车通常的行驶模式为牵引-巡航-惰行-制动, 可转换为最优控制问题.文献[3]采用极大值原理, 对连续时间的列车动力学模型进行求解, 画出了控制切换图, 求出了列车在完全牵引、部分牵引、惰行、部分制动和完全制动这些控制之间切换的条件.文献[4]则采用伪谱法(Pseudospectral method)对列车运行对应的最优控制问题进行求解, 与列车时刻表规划相结合, 起到了很好的节能效果.若巡航中存在过于陡峭的轨道, 需要中断巡航模式, 进行牵引或制动.文献[5]使用了综合扰动分析法, 证明了能耗函数的凸性, 设计了确定陡峭坡道上最优速度转换点的策略.

与此同时, 智能优化算法也在列车速度曲线优化问题上得到广泛应用^[6].文献[7]采用遗传算法对列车运行曲线进行优化, 研究了能耗指标与迭代次数的关系.文献[8]同样选择遗传算法, 以触发惰行的速度、牵引力比例、制动力比例为参数, 进行了列车运行曲线的优化, 结果表明加速比率与制动比率会影响列车运行的能耗.文献[9]针对列车运行过程中存在干扰的情况, 建立了以节能为目标的速度运行曲线优化模型, 并采用遗传算法进行求解, 最后得到了良好的节能效果.文献[10]以能耗、舒适性等指标形成多目标优化函数, 采用粒子群优化算法计算ATO目标曲线.文献[11]使用了动态规划、遗传算法和蚁群算法这3种算法对列车运行曲线进行优化, 并对3种算法的性能进行分析和比较, 其中蚁群优化算法在稳定性与能耗方面具有较好的优化效果.文献[12]则对遗传算法进行了改进, 通过准点调整和局部搜索, 引导种群进化方向, 提高了收敛速度.智能算法在优化过程中需要大量的迭代计算, 用时较长, 无法满足ATO车载设备在线或实时优化的应用需求, 但可离线生成目标速度曲线提前存储于ATO的车载设备中^[13].

此外, 文献[14]以能耗和舒适度为目标函数, 采用混合整数线性规划(Mixed Integer Linear Programming, MILP)和伪谱法对列车运行速度曲线进行求解, 结果表明了混合整数规划算法能得到与伪谱法相近的优化效果, 且计算时间非常短, 可满足在线优化的时间要求.文献[15]将速度、距离划分为多个等间隔的区间, 构造了两个相邻站之间的速度距离网络, 建立了随机约束最短路径模型, 通过基于采样的方法描述运行过程中的一些不确定性, 利用拉格朗日松弛(Lagrangian Relaxiation, LR)算法求解.并通过仿真测试了对算法的效果, 结果表明算法运算时间与采样数呈近似线性的正相关.

相比于连续的列车运行模型, 离散的速度距离网络模型便于计算.本文作者对列车于两站之间的运行过程建立速度距离网络, 将列车运行曲线优化问题转化为整数规划问题, 采用拉格朗日松弛与最短路径算法对问题进行求解, 与成熟的优化软件CPLEX的求解效果进行比较.此外, 本文还与文献[13]提出的混合整数规划算法进行对比, 证明基于速度距离网络模型的可行性和优越性.由于速度离散步长对网络复杂度的影响较大, 为提高运算速度, 提出了基于粗粒度网络最优解的小邻域细粒度网络构建.并基于北京地铁亦庄线的线路数据设计了测试案例, 评估网络重构方法的有效性.

1 列车运行曲线优化问题建模

本文将列车视为单质点, 根据牛顿运动定律, 列车的运动学模型为

$mρ \frac{d v (t)}{d t} = F (t) - F_{b} - F_{l}$ (1)

$\frac{d s (t)}{d t} = v (t)$ (2)

式中: $m$ 为列车质量; $ρ$ 为旋转质量因子; $v$ 为列车速度; $t$ 为时间; $F$ 为列车牵引力或者制动力; $F_{b}$ 为列车所受基本阻力; $F_{l}$ 为列车所受线路附加阻力; $s$ 为列车位置. $F_{b}$ 主要由车型决定, 包括列车轴颈部所受的摩擦阻力、轮轨间的滑动阻力、由于弹性波产生的滚动阻力、由于冲击振动产生的阻力以及空气阻力, 可表示为^[13]

$F_{b} = m \cdot (a_{1} + a_{2} \cdot v^{2})$ (3)

式中:参数 $a_{1}, a_{2}$ 由列车动力学特性与风速决定, 可通过列车运行数据计算. $F_{l}$ 主要受线路因素的影响, 包括因坡度产生的坡道附加阻力、曲线附加阻力、隧道空气附加阻力等.本文中的线路附加阻力仅考虑坡道附加阻力, 其计算如下

$F_{l} = \frac{img}{1000}$ (4)

式中:i为坡度千分数, 它可近似为与列车位置s相关的分段函数, 具体为

$i (s) = \{\begin{array}{l} i_{1}, 0 \leq s < s_{1} \\ i_{2}, s_{1} \leq s < s_{2} \\ ︙ \\ i_{n}, s_{n - 1} \leq s \leq s_{n} \end{array}$ (5)

本文考虑的列车运行曲线优化问题是在确保准时到站和发车的前提下, 以列车站间运行的牵引能耗最小为优化目标.以 $F_{t}$ 表示牵引力, 则列车在时间段 $[0, T]$ 内的牵引能耗为

$E = \overset{T}{\int_{0}} F_{t} (t) \cdot v (t) d t$ (6)

根据式(1)得

$F = F_{b} + F_{l} + mρ \frac{d v}{d t}$ (7)

当 $F > 0$ 时, $F$ 为牵引力, 因此

$F_{t} = \max \{F_{b} + F_{l} + mρ \frac{d v}{d t}, 0\}$ (8)

除了目标函数外, 列车运行曲线优化问题还需考虑诸多的约束条件, 如限制速度、最大牵引力、运行时间、始端约束、终端约束等, 具体如下:

$F_{\min} \leq F (t) \leq F_{\max} (v (t))$ (9)

$0 \leq v (t) \leq v_{\max} (s (t))$ (10)

$v (0) = 0$ (11)

$v (T) = 0$ (12)

$s (0) = 0$ (13)

$s (T) = s_{d}$ (14)

式中: $F_{\min}$ 为最大制动力(负数); $F_{\max} (v)$ 为最大牵引力(速度 $v$ 的非线性函数); $v_{\max} (s (t))$ 为位置 $s (t)$ 处的最大限速; $T$ 为列车在本站间的运行时分; $s_{d}$ 为站间距.

2 离散速度距离网络构建

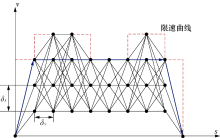
为求解上一节提出的优化问题, 同时将距离和速度进行离散化, 建立一个离散的速度距离网络, 如图1所示.这里采用等间隔离散的方式对距离与速度进行离散, 并根据列车的连续动力学模型确定各个节点的可行弧段(对于网络中两个距离坐标相邻的节点, 如果其速度变化符合列车动力学模型, 则添加连接该两节点的弧段), 并将列车在每个离散距离区段内的运行过程均近似为匀加速、匀速或匀减速运动, 线路限速、基本阻力和附加阻力等均在构建速度-距离弧段时予以考虑.此外, 列车在各离散距离区段内可根据实际情况选择对应的工况以最小化列车运行能耗.因此, 本文所构建的速度-距离网络符合列车的连续动力学特性, 且满足不同工况之间的转换关系.

	Figure Option View Download New Window
	图1 相邻两站间的速度-距离网络示意图Fig.1 Speed-distance network between two adjacent stations

对于速度距离网络模型, 设每个离散距离区段的长度为 $δ_{s}$ , 每个速度区段的长度为 $δ_{v},$ 将列车在离散区段中的运动近似为匀加速、匀速或匀减速运动, 则对于速度距离网络上的一条连接节点 $i$ 与 $j$ 的弧 $(i, j)$ , 节点 $i$ 与 $j$ 速度分别为 $v_{i}, v_{j}$ , 位置分别为 $s_{i}, s_{j}$ , 由式(2)可得弧上运行时间为

$t_{i, j} = \frac{2 δ_{s}}{v_{i} + v_{j}}$ (15)

加速度为

$\frac{d v (t)}{d t} = \frac{{v_{j}}^{2} - {v_{i}}^{2}}{2 δ_{s}}$ (16)

在该弧上运行消耗的能量为

$E_{i, j} = \overset{s_{j}}{\int_{s_{i}}} F_{t} d s$ (17)

引入0-1变量 $y_{i, j}$ 表示列车速度曲线是否包含弧 $(i, j)$ .若包含, 则 $y_{i, j}$ 为1; 否则为0.

对于速度距离网络模型, 优化问题的目标函数如下

$E = \sum_{(i, j) \in A} E_{i, j} \cdot y_{ij}$ (18)

式中: $A$ 为所有弧段的集合.

约束条件如下:

1)流平衡约束.

由于除起点 $o$ 和终点 $d$ 外, 列车在正常运行情况下驶入一个节点后必会驶出该节点, 则可得流平衡约束为

$\sum_{(i, j) \in A} y_{i, j} - \sum_{(j, k) \in A} y_{j, k} = \{\begin{array}{l} 1, j = d \\ - 1, j = o \\ 0, 其他 \end{array}$ (19)

2)时间约束.

列车速度曲线的总用时需满足给定的时间限制

$\sum_{(i, j) \in A} y_{i, j} \cdot t_{i, j} \leq T$ (20)

通过速度-距离网络模型, 优化问题转化为一个在速度-距离网络中有时间约束的最短路径问题, 起点为节点 $o$ , 终点为节点d, 在弧(i, j)上移动的成本为 $E_{i, j} .$

3 求解算法

通过速度-距离网络的构建, 列车运行曲线优化问题转化为整数规划问题, 其中决策变量 $y_{i, j}$ 为0-1整数变量, 约束条件和目标函数均为线性.针对此优化问题, 采用拉格朗日松弛与最短路径算法进行求解, 并与优化软件CPLEX的求解效果进行对比.

3.1 拉格朗日松弛

时间约束导致上一节的最短路径问题不便于求解, 采用拉格朗日松弛算法对时间约束进行松弛, 将其作为惩罚项加入目标函数中, 具体为

$R (λ) = \min [\sum_{(i, j) \in A} E_{i, j} \cdot y_{i, j} + λ (\sum_{(i, j) \in A} y_{i, j} \cdot t_{i, j} - T)]$ (21)

式中:拉格朗日乘子 $λ \geq 0$ .由于 $λT$ 为常数项, 优化时无需考虑, 则优化问题可写为

$\{\begin{array}{l} R' (λ) = \min \sum_{(i, j) \in A} (E_{i, j} + λ \cdot t_{i, j}) \cdot y_{i, j} \\ s.t. \sum_{(i, j) \in A} y_{i, j} - \sum_{(j, k) \in A} y_{j, k} = \{\begin{array}{l} 1, j = d \\ - 1, j = o \\ 0, 其他 \end{array} \end{array}$ (22)

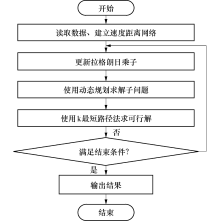
本文使用动态规划算法对式(22)中的最短路径问题进行求解, 采用反向递推的方式, 动态规划子问题为求解从某个节点到终点的最短路径, 并将动态规划算法的状态定义为某个节点至终点最短路径对应的能耗.这里以花销表示路径的能耗与拉格朗日松弛带来的惩罚项之和, 将C(i)定义为节点i到终点d的最短路径的花销, $C_{A} (i, j)$ 定义为连接节点i与j的弧的花销.算法的总流程图如图2所示.采用动态规划求解式(22)的优化问题的流程具体如下:

	Figure Option View Download New Window
	图2 拉格朗日松弛算法流程Fig.2 Flow chart of Lagrangian relaxation

算法:动态规划

1:C (d)设为0.计算每个弧段的花销C_A(i, j);

2: for n=1 to $s_{d} / δ_{s}$

3: while s_i=s_d-n· δ _s do

4:寻找使[C(j)+ C_A(i, j)]最小的节点j, 找到后, C(i)=C (j)+ C_A(i, j), 存储路径;

5: i=i+1;

6: end while

7: end for

由于该对偶问题的最优解(拉格朗日松弛的下界)可能不满足时间约束条件, 因此需要采用启发式算法构建可行解(上界).本文采用k条最短路径法, 通过查找第k-1条最短路径上节点的邻近点, 寻找第k条最短路径, 直至找到满足时间约束的路径.为了让k条最短路径运行时间满足约束, 在邻近点中只需考虑速度比第k-1条路径节点速度更高的邻近节点, 具体算法流程如下

算法:k条最短路径算法

1: k=2;

2: while 备选路径中无可行解

3: for 第k-1条最短路径上的节点i

4: if 存在节点j满足 $v_{j} = v_{i} + δ_{v}$ & & $s_{j} = s_{i}$

5: 将j存入备选节点集合中, 并以其代替第k-1条最短路径上的节点i, 得到备选路径

6: end if

7: end for

8:end while

9:寻找备选路径中能耗最小的可行解

在得到问题的上界和下界之后, 使用次梯度更新拉格朗日乘子, 如下

$λ_{n + 1} = λ_{n} + α_{n} \cdot \max {\sum_{(i, j) \in A} y_{i, j} \cdot t_{i, j} - T, 0}$ (23)

式中: $α_{n} 为第 n$ 次迭代时的步长.应用LR算法时, 预先设置阈值 $ε$ 以及迭代次数的上限, 当对偶问题的解与可行解之间的偏差程度小于 $ε$ 时, 或者迭代次数达到次数的上限时, 算法结束.

3.2 小邻域的速度距离网络精细重构

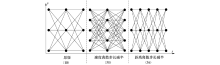
在离散速度距离网络的构建中, 距离、速度离散步长的选取对网络规模、计算复杂度、求解精度等有直接影响.与距离离散步长不同的是, 速度离散步长的降低对网络的规模影响更大, 如图3所示.括号中为弧段数.若为了提高解的质量而直接降低速度离散步长, 会使得计算时间显著提高.为了提升计算效率, 本文提出基于不同粒度速度距离网络的列车运行曲线优化方法.首先, 离线构建粗粒度的速度距离网络, 对列车运行速度曲线进行求解, 并基于计算出的最优列车运行速度曲线, 在其邻域内构建更为精细的速度距离网络, 增大可选节点的数目、扩大可行域, 在计算时间消耗不大的情况下提升求解质量.

	Figure Option View Download New Window
	图3 离散步长对弧段的影响示例Fig.3 Sample of step size’ s influence

4 仿真案例

4.1 参数设置

北京地铁亦庄线运行DKZ32型列车, 编组方式为B型车6节编组, 列车质量为194.295 t^[16], 旋转质量因子为1.06.全线最高时速不超过80 km/h.本文根据亦庄线的线路和车辆数据, 对宋家庄站至肖村站区间内的列车运行曲线进行优化.宋家庄站与肖村站的站间距为2 631 m, 站间坡度变化如表1所示.

表1 宋家庄站与肖村站间坡度 Tab.1 Slope between Songjiazhuang Station and Xiaocun Station

本文用C++语言实现基于拉格朗日(LR)算法的列车运行曲线优化, 并采用CPLEX 12.8直接对基于速度距离网络的0-1整数规划问题进行求解(ILP).配置为:计算机内存为16 GB, 处理器主频为3.40 GHz, 操作系统为Windows 7(64位).计划运行时间为180 s, 以等间隔方式将路程离散为20个区间, 离散步长为131.55 m.速度距离网络模型以0.2 m/s为速度离散步长, ILP算法调用离线生成的速度距离网络, 而LR算法采用在线生成速度距离网络的策略, 并分别计算重构与不重构网络的结果, 重构网络的速度离散步长为0.02 m/s.

为分析本文所提出模型与算法的效果, 将其与遗传算法(GA)和混合整数线性规划算法(MILP)进行结果对比.GA基于文献[8], 本文将列车的运行工况分为牵引、巡航、惰行与制动, 对牵引最高速度、隋行最低速度、巡航距离、牵引过程中牵引力占最大牵引力的比例、制动过程中制动力占最大制动力的比例进行编码.MILP基于文献[14], 将列车曲线优化问题建立成线性近似的距离离散模型并求解.

4.2 模型结果对比

目标运行时间为180 s情况下, 4种不同方法得到的列车运行曲线和牵引力/制动力曲线如图4所示.可见, 速度距离网络模型的求解结果能完全满足限速约束, 而线性近似的距离离散模型则有略微超过限速的部分.除遗传算法有多次牵引以外, 其他四种方法求解出的结果具有相近的控制切换点.

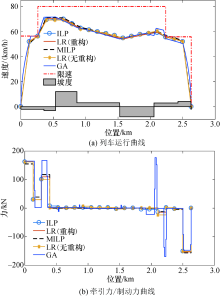	Figure Option View Download New Window
	图4 宋家庄— 肖村站间不同算法计算结果Fig.4 Calculation results of different algorithms between Songjiazhuang Station and Xiaocun Station

为分析运行时间变化对能耗的影响, 调整两个站间的列车计划运行时间, 具体为160、170、180、190 s和200 s, 得到的列车运行曲线和牵引力/制动力曲线如图5所示, 具体计算结果如表2所示.从结果中可以看到, 相较于线性近似的距离离散模型, 速度距离网络能更好地满足限速、运行时间、起点与终点速度约束, 说明速度距离网络具有误差较小的优势.对比未使用重构的LR算法与ILP算法的结果, 可见相同离散步长情况下, 使用离线生成的速度距离网络的ILP运算时间更快, 且能耗更小.从重构网络的LR算法的结果可以看到, 降低速度离散步长, 能使运行能耗更低.当速度离散步长较小时, 在运行时间小于目标运行时间的情况下, 即使MILP存在超速现象, 重构网络的LR算法所得能耗仍比MILP的结果更好.遗传算法生成的列车速度曲线能耗相对较高, 计算时间较长, 因此, 基于距离离散模型的MILP算法、基于速度距离网络的拉格朗日松弛算法、ILP算法的求解效果比传统的遗传算法更好.

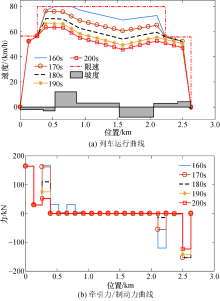	Figure Option View Download New Window
	图5 不同目标运行时间下宋家庄— 肖村站间使用LR与重构策略计算结果Fig.5 Calculation results of LR algorithm with reconstruction strategy for different target running times between Songjiazhuang Station and Xiaocun Station

表2 不同目标运行时间的运算结果 Tab.2 Results with different running times

为了评估速度离散步长对速度距离网络模型的影响以及重建速度距离网络策略的效果, 使用不同的速度步长进行测试.测试的结果见表3.

表3 不同速度离散步长的运算结果 Tab.3 Results with different step sizes

计算结果表明, 在运算速度方面, 速度离散步长较大时, ILP运算速度较快; 而离散步长较小时, ILP计算时间显著提高, 采用重建网络策略的LR运算较快.在能耗方面, 相比于同离散步长的LR, ILP有一定优势.对于使用重建网络策略与未使用该策略的LR, 前者重建的离散步长与后者离散步长相同时, 能获得相近的能耗.由此可见, 重建策略在降低计算时间的同时能保证解的质量.

5 结论

1)采用速度-距离网络模型实现了节能列车运行曲线求解, 并对不同算法进行了对比.将列车在两站间运行时的速度、距离离散化, 建立了速度距离网络.由此, 将列车运行曲线优化问题转化为最短路径问题, 进而使用ILP与基于LR的算法对问题进行求解.由于缩短速度离散步长会使得弧段数大量增加, 采用了基于粗粒度网络的解, 重建细粒度网络并求解的策略, 使速度距离模型的求解速度得到提高.

2)基于北京地铁亦庄线的数据进行了仿真.结果表明, 相比与用MILP解距离离散并线性近似的模型, 速度-距离网络模型的优点在于误差更小, 能精确满足各项约束, 且在运行时间小于目标运行时间、速度离散步长较小的情况下, 其能耗更小.相比于传统的遗传算法, 速度距离网络模型节能性更好.证明速度距离网络模型在列车运行曲线优化方面有一定优势.对于速度距离网络模型, 相同速度离散步长情况下, ILP能耗比LR稍小.速度离散步长较大时, ILP运算速度较快, 比MILP稍慢; 步长较小时, 采用重建网络策略的LR比未采用此策略的LR与ILP更快, 且解的质量相近.

由于调用离线建立的速度距离网络数据的ILP算法速度较快, 有望应用于列车运行曲线的实时优化中.后续的研究中, 可以对算法与模型进行优化, 提升运算速度, 以满足实时计算的要求.此外, 可分析雨雪条件对列车运行的影响, 通过修改速度距离网络, 模拟雨雪情况, 对列车运行进行鲁棒性优化.

参考文献

文献列表

[1]	唐涛, 黄良骥. 列车自动驾驶系统控制算法综述[J]. 铁道学报, 2003, 25(2): 98-102. TANG Tao, HUANG Liangji. A survey of control algorithm for automatic train operation[J]. Journal of the China Railway Society, 2003, 25(2): 98-102. (in Chinese) [本文引用:1]
[2]	ICHIKAWA K. Application of optimization theory for bounded state variable problems to the operation of train[J]. Japan Society of Mechanical Engineers, 1968, 11(47): 857-865. [本文引用:1]
[3]	LIU R, GOLOVITCHER I M. Energy-efficient operation of rail vehicles[J]. Transportation Research Part A: Policy and Practice, 2003, 37(10): 917-932. [本文引用:1]
[4]	WANG P, GOVERDE R M P. Multi-train trajectory optimization for energy-efficient timetabling[J]. European Journal of Operational Research, 2018, 272(2): 621-635. [本文引用:1]
[5]	ALBRECHT A R, HOWLETT P G, PUDNEY P J, et al. Energy-efficient train control: from local convexity to global optimization and uniqueness[J]. Automatica, 2013, 49(10): 3072-3078. [本文引用:1]
[6]	金炜东, 靳蕃, 李崇维, 等. 列车优化操纵速度模式曲线生成的智能计算研究[J]. 铁道学报, 1998, 20(5): 48-53. JIN Weidong, JIN Fan, LI Congwei, et al. Study on intelligent computation of velocity schema curve of optimization operation for train[J]. Journal of the China Railway Society, 1998, 20(5): 48-53. (in Chinese) [本文引用:1]
[7]	杨昌休, 刘莉, 王长林. 基于遗传算法对高速列车速度曲线的优化[J]. 铁路计算机应用, 2012, 1(1): 9-12. YANG Changxiu, LIU Li, WANG Changlin. Optimization of high-speed train speed curve based on genetic algorithm[J]. Railway Computer Application, 2012, 1(1): 9-12. (in Chinese) [本文引用:1]
[8]	BOCHARNIKOVY V, TOBIAS A M, ROBERTS C, et al. Optimal driving strategy for traction energy saving on DC suburban railways[J]. IET Electric Power Applications, 2007, 1(5): 675-682. [本文引用:2]
[9]	付印平, 高自友, 李克平. 路网中的列车节能操纵优化方法研究[J]. 交通运输系统工程与信息, 2009, 9(4): 90-96. FU Yinping, GAO Ziyou, LI Keping. Optimization method of energy saving train operation for railway network[J]. Journal of Transportation Systems Engineering and Information Technology, 2009, 9(4): 90-96. (in Chinese) [本文引用:1]
[10]	安志强. ATO目标速度曲线优化及跟随控制研究[D]. 成都: 西南交通大学, 2011. AN Zhiqiang. Study on optimization of ATO target speed curve and its tracking control[D]. Chengdu: Southwest Jiaotong University, 2011. (in Chinese) [本文引用:1]
[11]	LU S, HILLMANSEN S, HO T K, et al. Single-train trajectory optimization[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(2): 743-750. [本文引用:1]
[12]	纪云霞, 孙鹏飞, 毛畅海, 等. 基于改进遗传算法的列车运行曲线优化[J]. 计算机与现代化, 2018, 276(8): 5-11. JI Yunxia, SUN Pengfei, MAO Changhai, et al. Optimization of train operation profile based on improved genetic algorithm[J]. Computer and Modernization, 2018, 276(8): 5-11. (in Chinese) [本文引用:1]
[13]	孟建军, 银铭, 祁文哲, 等. 基于遗传算法的高速列车ATO追溯目标曲线优化[J]. 计算机工程与应用, 2016, 52(21): 247-251. MENG Jianjun, YIN Ming, QI Wenzhe, et al. Optimization of tracing target curve of high-speed train ATO based on genetic algorithm[J]. Computer Engineering and Applications, 2016, 52(21): 247-251. (in Chinese) [本文引用:3]
[14]	WANG Y, SCHUTTER B D, BOOM T J, et al. Optimal trajectory planning for trains—a Pseudospectral method and a mixed integer linear programming approach[J]. Transportation Research Part C Emerging Technologies, 2013, 29(4): 97-114. [本文引用:2]
[15]	WANG L, YANG L, GAO Z, et al. Robust train speed trajectory optimization: a stochastic constrained shortest path approach[J]. Frontiers of Engineering Management, 2017, 4(1): 408-417. [本文引用:1]
[16]	唐涛, 荀径, 曹芳, 等. 北京地铁亦庄线列车节能驾驶研究[J]. 北京交通大学学报, 2016, 40(4): 19-24. TANG Tao, XUN Jing, CAO Fang, et al. Research on Energy-efficient driving strategy in Beijing YizhuangLine[J]. Journal of Beijing Jiaotong University, 2016, 40(4): 19-24. (in Chinese) [本文引用:1]

2003

0.0

... 而最优化速度距离运行曲线是列车自动运行(Automatic Train Operation,ATO)系统的基础之一^[1],在节能方面发挥着重要的作用 ...

1968

0.0

... 自1968年Ichikawa^[2]首次采用最大值原理对列车运行曲线优化以来,研究学者对列车运行曲线优化展开了广泛而深入的研究 ...

2003

0.0

... 文献[3]采用极大值原理,对连续时间的列车动力学模型进行求解,画出了控制切换图,求出了列车在完全牵引、部分牵引、惰行、部分制动和完全制动这些控制之间切换的条件 ...

2018

0.0

... 文献[4]则采用伪谱法(Pseudospectral method)对列车运行对应的最优控制问题进行求解,与列车时刻表规划相结合,起到了很好的节能效果 ...

2013

0.0

... 文献[5]使用了综合扰动分析法,证明了能耗函数的凸性,设计了确定陡峭坡道上最优速度转换点的策略 ...

1998

0.0

... 与此同时,智能优化算法也在列车速度曲线优化问题上得到广泛应用^[6] ...

2012

0.0

... 文献[7]采用遗传算法对列车运行曲线进行优化,研究了能耗指标与迭代次数的关系 ...

2007

0.0

... 文献[8]同样选择遗传算法,以触发惰行的速度、牵引力比例、制动力比例为参数,进行了列车运行曲线的优化,结果表明加速比率与制动比率会影响列车运行的能耗 ...

... GA基于文献[8], 本文将列车的运行工况分为牵引、巡航、惰行与制动,对牵引最高速度、隋行最低速度、巡航距离、牵引过程中牵引力占最大牵引力的比例、制动过程中制动力占最大制动力的比例进行编码 ...

2009

0.0

付印平, 高自友, 李克平. 路网中的列车节能操纵优化方法研究[J]. 交通运输系统工程与信息, 2009, 9(4): 90-96.

Yinping

, GAO

Ziyou

, LI

Keping

. Optimization method of energy saving train operation for railway network[J]. Journal of Transportation Systems Engineering and Information Technology, 2009, 9(4): 90-96. (in Chinese)

Abstract In railway network, trains running through stations may be disturbed by trains in other lines. This paper investigates energy saving train operation under disturbance condition. According to the mathematical description of the problem and dynamic equation for train movement, the authors propose an optimization model of energy saving train operation. A changeable chromosome length genetic algorithm (GA) and table of control mode list are applied to solve the optimization problem. The simulation is carried out, and the speed-position curve of disturbed train is compared with that of train that moves normally. The variation of speed with time is analyzed. Some principles for energy saving are revealed in speed-position curve and energy-position curve. At last, the simulation result is compared with that obtained by other methods. The comparison shows that the changeable chromosome length GA is an effective method to be applied in energy saving train operation.

... 文献[9]针对列车运行过程中存在干扰的情况,建立了以节能为目标的速度运行曲线优化模型,并采用遗传算法进行求解,最后得到了良好的节能效果 ...

2011

0.0

... 文献[10]以能耗、舒适性等指标形成多目标优化函数,采用粒子群优化算法计算ATO目标曲线 ...

2013

0.0

... 文献[11]使用了动态规划、遗传算法和蚁群算法这3种算法对列车运行曲线进行优化,并对3种算法的性能进行分析和比较,其中蚁群优化算法在稳定性与能耗方面具有较好的优化效果 ...

2018

0.0

... 文献[12]则对遗传算法进行了改进,通过准点调整和局部搜索,引导种群进化方向,提高了收敛速度 ...

2016

0.0

孟建军, 银铭, 祁文哲, 等. 基于遗传算法的高速列车ATO追溯目标曲线优化[J]. 计算机工程与应用, 2016, 52(21): 247-251.

MENG

Jianjun

, YIN

Ming

, QI

Wenzhe

, et al. Optimization of tracing target curve of high-speed train ATO based on genetic algorithm[J]. Computer Engineering and Applications, 2016, 52(21): 247-251. (in Chinese)

Due to the differences of operating environment that cause energy consumption, comfort, punctuality and accurate parking in high-speed trains running process, this paper uses genetic algorithm to optimize the energy saving curve and multi-objective curve, combined with the train traction calculating equation and selected line constraint conditions to get the target curve of ATO traced. The results show that genetic algorithm which optimizes the condition of train conversion makes the proportion of coasting increased, achieving train energy-saving operation. Compared with energy-saving operation, multi-objective one can be better to ensure train operation key indicators in comfort, punctual and accurate park.

1.School of Mechanical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China 2.Mechatronics T&R Institute, Lanzhou Jiaotong University, Lanzhou 730070, China 3.Engineering Technology Center for Informatization of Logistics & Transport Equipment, Lanzhou 730070, China

对于高速列车在运行过程中因为运行环境造成能耗、舒适、准时和准确停车等指标的不同，运用遗传算法对列车运行的节能性曲线和多目标运行曲线优化，结合列车牵引计算方程和选定的线路约束条件仿真得到列车ATO所要追溯的目标曲线。结果表明：通过遗传算法优化工况转换点使得列车运行中的惰行比例增加，可以实现列车节能运行，与节能性目标相比，多目标可以较好地保证列车运行中的舒适性，准时性和准确停车等关键性指标。

... 智能算法在优化过程中需要大量的迭代计算,用时较长,无法满足ATO车载设备在线或实时优化的应用需求,但可离线生成目标速度曲线提前存储于ATO的车载设备中^[13] ...

... 此外,本文还与文献[13]提出的混合整数规划算法进行对比,证明基于速度距离网络模型的可行性和优越性 ...

... Fb主要由车型决定,包括列车轴颈部所受的摩擦阻力、轮轨间的滑动阻力、由于弹性波产生的滚动阻力、由于冲击振动产生的阻力以及空气阻力,可表示为^[13] ...

2013

0.0

... 此外,文献[14]以能耗和舒适度为目标函数,采用混合整数线性规划(Mixed Integer Linear Programming,MILP)和伪谱法对列车运行速度曲线进行求解,结果表明了混合整数规划算法能得到与伪谱法相近的优化效果,且计算时间非常短,可满足在线优化的时间要求 ...

... MILP基于文献[14],将列车曲线优化问题建立成线性近似的距离离散模型并求解 ...

2017

0.0

... 文献[15]将速度、距离划分为多个等间隔的区间,构造了两个相邻站之间的速度距离网络,建立了随机约束最短路径模型,通过基于采样的方法描述运行过程中的一些不确定性,利用拉格朗日松弛(Lagrangian Relaxiation,LR)算法求解 ...

2016

0.0

... 295 t^[16],旋转质量因子为1 ...