边缘直线拟合确定鱼眼镜头光心算法

引用本文

林春雨, 高奕, 王欣, 黄奇, 王鑫, 赵耀. 边缘直线拟合确定鱼眼镜头光心算法[J]. 北京交通大学学报, 2017,41(2): 8-14.
LIN Chunyu, GAO Yi, WANG Xin, HUANG Qi, WANG Xin, ZHAO Yao. An algorithm to determine the fish-eye lens optical center using edge straight-line-fitting[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2017,41(2): 8-14.
Doi:10.11860/j.issn.1673-0291.2017.02.002 复制到剪切板

Permissions

边缘直线拟合确定鱼眼镜头光心算法

林春雨¹, 高奕¹, 王欣¹, 黄奇², 王鑫², 赵耀¹

1.北京交通大学信息科学研究所,北京 100044

2.北京鑫洋泉电子科技有限公司,北京100038

第一作者:林春雨(1979—),男,辽宁绥中人,副教授,博士.研究方向为图像视频处理和图像视频编解码. email: cylin@bjtu.edu.cn.

收稿日期: 2016-10-31

基金: 国家自然科学基金(61402034,61210006,61501379); 中央高校基本科研业务费专项资金(2015JBM032, 2015JBZ002)

摘要

为了去除鱼眼图像存在严重的畸变,需要对鱼眼相机进行标定,本文在已知相机参数表的前提下,提出了一种边缘直线拟合来标定最重要的镜头光心坐标算法.该算法利用像素点在图像平面上的物理尺寸及相机焦距,确定相机标定内参矩阵中水平轴和竖直轴的尺度因子.在部分内参已知的情况下,对光心的横、纵坐标在给定范围内进行遍历,校正点到拟合直线加权距离和最小的点,即为所求的光心坐标值.实验结果表明: 与常规的标定算法相比,该算法得到的光心坐标减少了由于不精确参数使用带来的累积误差,提高了相机标定结果的精度.

关键词: 信息处理; 标定; 光心坐标; 边缘直线拟合; 坐标变换; 畸变; 鱼眼镜头

中图分类号:TP391 文献标志码:A 文章编号:1673-0291(2017)02-0008-07

An algorithm to determine the fish-eye lens optical center using edge straight-line-fitting

LIN Chunyu¹, GAO Yi¹, WANG Xin¹, HUANG Qi², WANG Xin², ZHAO Yao¹

1. Institute of Information Science, Beijing Jiaotong University, Beijing 100044, China

2. Beijing Xinyangquan Electronic Technology Company Limited, Beijing 100038, China

Fund:National Natural Science Foundation of China(61402034,61210006,61501379); Fundamental Research Funds for the Central Universities (2015JBM032, 2015JBZ002)

Abstract

In order to remove the distortion in fish-eye image, the camera calibration is required. We put forward an algorithm to determine fish-eye lens optical center using the edge straight-line-fitting technology with a given camera parameters table. This algorithm utilizes the physical size of each pixel in the image plane as well as the camera focal length. Therefore, the scale factor in horizontal and vertical axes of the reference matrix can be determined. With some provided parameters, the optic center can be determined by traversing the pixel coordinates within given range. The optic center, which made the weighted distance between corrected points and fitted straight lines smallest, is needed. Experimental results show that compared with the conventional camera calibration algorithm, this algorithm reduces the accumulation of errors due to the using of inaccurate parameters and makes the calibration results more accurate.

Keyword: information processing; calibration; optic center coordinate; edge straight-line-fitting; coordinate transformation; distortion; fish-eye lens

文章图片

鱼眼镜头是一种超广角镜头, 因其前镜片呈抛物状向镜头前部凸出, 与鱼的眼睛十分相似而得名.鱼眼镜头的视角可达甚至超过180° , 且其价格经济实惠, 现已被广泛使用.同时, 随着计算机软硬件技术的持续发展, 三维重建技术^{[1, 2]}成为数字媒体、科学计算、医学图像处理、计算机视觉等领域的共性科学问题和核心技术.为满足该技术对模型的复杂度和真实度的要求, 研究者将具有优良特性的鱼眼相机和三维重建技术相结合来进行深度恢复和全景漫游^[3], 应用于虚拟现实、行车安全及视觉监控等领域^[4].

虽然鱼眼镜头可以获得很大的视角, 但是根据物理成像的规律, 焦距越短, 视角越大, 所以, 鱼眼相机采集的图像通常都引入了桶形畸变^[5], 所成的图像除了光心四周基本不变外, 其他图像区域都存在一定程度上的畸变^[6], 图像不易被理解.因此, 在使用鱼眼图像之前, 首先需要对鱼眼镜头的相关参数进行精确的校正, 这个校正过程在计算机视觉中称为相机标定.相机标定所得的参数将直接影响随后的图像理解过程, 进而影响实际应用主观感受和视觉体验的真实性.

相机标定的内容包括确定相机外部和内部参数等.外部参数指相机的位置和姿态, 包括相机的旋转和平移等; 内部参数是相机内的方位元素和镜头的光学畸变参数, 包括焦距和光心坐标等.其中, 光心是最重要的参数, 它直接影响标定的精准度.现行的标定算法流程如下:为了提高标定的精度, 从不同视角采集多幅鱼眼图像, 使整个特征点集合的范围尽可能的遍布整个图案, 根据每幅标定图像中参照物的位置来建立世界坐标系(不同图像对应的世界坐标系不同), 利用多幅标定图像来同时求解, 得出相机的内外参数, 完成相机标定.但这种方法存在较大的局限性:在许多实际应用场景下, 没办法从多个视角获得鱼眼图像.因此, 该方法不能运用于行车安全和监控等对实时性要求很高的领域, 并且, 当光心坐标的求解不够精确时, 将会产生误差的累积, 影响整个标定的精确性^[7].

目前针对鱼眼相机标定的算法有很多研究成果.文献[8]提出了一种鱼眼标定方法, 但该方法仅考虑了径向变形而没有考虑到切向变形等因素, 得到的标定参数精度较低, 无法应用于一些精度要求高的标定场合.文献[9]提出一种通用的基于抛物面模型的鱼眼图像校正算法, 对鱼眼图像中代表空间水平或竖直直线的曲线进行了采样, 并拟合出抛物面的直线, 但是根据文献的实验结果来看, 该方法并没有很好地复原弯曲的直线, 校正效果不够精确.文献[10]提出了平面校正方法, 该方法校正的缺点是比较受视野大小的局限^[11].现行的方法及新的研究成果将相机的各个参数等同视之, 没有注意到光心坐标的重要性.

本文作者针对现有标定技术的不足, 在已知粗略相机参数表的情况下, 以光心坐标为切入点, 提出一种边缘直线拟合确定鱼眼镜头光心的方法, 通过提高光心坐标的精准性来得到更好的标定结果.整个过程可以仅用一幅图像即可实现.

1 相机标定算法的基础知识

1.1 理想的相机成像原理

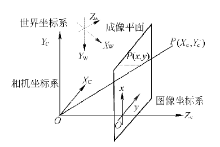
相机拍摄图像的过程, 实际上是一个光学成像的过程, 其中涉及到4个坐标系:世界坐标系、相机坐标系、图像坐标系和像素坐标系^[12].

1)世界坐标系.系统的绝对坐标系.采集图像时, 相机被安放在实际的三维空间中, 所以需要世界坐标系( $X_{W}, Y_{W}, Z_{W}$ )来描述三维空间中物体的实际位置.

2)相机坐标系(光心坐标系).对镜头建立的三维坐标系.原点是相机的光学中心, $X_{C}$ 轴和 $Y_{C}$ 轴平行于镜头的成像平面, $Z_{C}$ 轴为相机的光轴( $X_{C}, Y_{C}, Z_{C}$ 轴的关系符合右手定则).

3)图像坐标系.对图像建立的坐标系. $X$ 轴和 $Y$ 轴平行于图像平面的两条垂直边, 用 $(x, y)$ 表示其坐标值.

4)像素坐标系. X、Y轴分别平行于图像坐标系的X、Y轴, 用(u, v)表示其坐标值.相机采集的图像将被存储为M× N的数组, M行N列的图像中每一个元素成为像素, 其值代表图像点的灰度.

4个坐标系之间的关系如图1所示^[13].

	Figure Option View Download New Window
	图1 坐标系关系示意图Fig.1 Coordinate system diagram

1.2 鱼眼相机成像过程

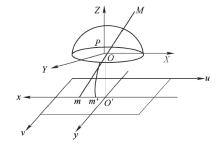
与透视投影不同, 鱼眼镜头的成像是非相似原理.将鱼眼镜头近似看成是一个半球模型, 取世界坐标系中一点 $M = (X_{W}, Y_{W}, Z_{W})$ , 它在相机坐标系上的映射点为 $P = (X_{C}, Y_{C}, Z_{C})$ , $M$ 点和 $P$ 点的投影关系如下式

$(\begin{array}{l} X_{C} \\ Y_{C} \\ Z_{C} \\ 1 \end{array}) = (\begin{array}{l} R & t \\ 0 & 1 \end{array}) (\begin{array}{l} X_{W} \\ Y_{W} \\ Z_{W} \\ 1 \end{array}) (1)$

式中: $R$ 是世界坐标系和相机坐标系之间的旋转矩阵; $t$ 是一个三维的平移向量^[14].

在点 $M$ 处放置一个点光源, 由该点发出光线首先经过相机光心 $O$ .由于光路弯曲, 光线在成像平面的投影点为 $m$ , 而一般透视投影的投影点为 $m'$ , 如图2所示.该投影关系为 $λm = g (K \cdot P)$ .

其中

$K = [\begin{array}{l} f_{x} & 0 & c_{x} \\ 0 & f_{y} & c_{y} \\ 0 & 0 & 1 \end{array}] (2)$

式中: $λ$ 为非零度因子; $K$ 为内参数矩阵; $f_{x}$ 和 $f_{y}$ 分别是图像水平轴和垂直轴的尺度因子; $c_{x}$ 和 $c_{y}$ 是图像坐标系原点在像素坐标系中的坐标.该投影过程是非线性的, 根据投影函数 $g$ 的不同, 可以提出不同的鱼眼相机模型.

	Figure Option View Download New Window
	图2 鱼眼相机投影模型示意图Fig.2 A model for the fish-eye camera projection

2 本文算法

本文算法具有一定的实用价值, 是针对全景汽车辅助驾驶系统、实时监控和三维重建等应用提出.由于这类应用对实时性的要求很高, 需采集多张图像的传统标定方法不可用.本文算法仅需一张图像, 便可达到很好的标定效果.

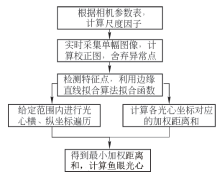
在给定的相机参数表中, 镜头光心即为成像平面的中心点.由于工艺限制, 以及后期镜头座的安装等问题, 经常造成镜头光心不准确, 如果将光心坐标直接作为参数代入到内参矩阵中进行后续使用, 就会存在累积误差, 从而大大影响随后相机的标定及畸变校正的精确性^[15].本文算法针对这个问题进行改善, 在部分相机参数已知的情况下, 基于边缘直线拟合技术, 更加简单和精确地计算鱼眼相机镜头的光心, 从而提高鱼眼相机标定的精确性.该算法的流程图如图3所示.

	Figure Option View Download New Window
	图3 算法流程图Fig.3 Flow chart of the proposed algorithm

2.1 内参矩阵参数的确定

根据相机坐标系和图像坐标系之间的转换关系, 内参矩阵 $K$ 可以转换为

$\begin{array}{l} K = [\begin{array}{l} f & 0 & 0 \\ 0 & f & 0 \\ 0 & 0 & 1 \end{array}] \times [\begin{array}{l} \frac{1}{d_{x}} & 0 & c_{x} \\ 0 & \frac{1}{d_{y}} & c_{y} \\ 0 & 0 & 1 \end{array}] (3) \\ f_{x} = \frac{1}{d_{x}} \times f (4) \\ f_{y} = \frac{1}{d_{y}} \times f (5) \end{array}$

因为相机参数表可以较为准确地提供每个像素点在图像平面水平轴和垂直轴方向上的物理尺寸 $d_{x} 、 d_{y}$ 及相机焦距 $f$ , 利用这些参数, 便可求解出 $f_{x}$ 和 $f_{y}$ .本实验所使用的鱼眼相机镜头型号为华科8067, 鱼眼镜头的一些重要参数为:有效像素矩阵756× 504; 像素尺寸6.35 μ m× 7.4 μ m; 图像有效面积4.8 mm× 3.73 mm (焦距 6.08 mm).

已知: $d_{x}$ =6.35 μ m, $d_{y}$ =7.4 μ m, $f$ =6.08 mm, 根据式(4)和式(5), 可以求得 $f_{x}$ =958 μ m, $f_{y}$ =822 μ m.这样求得的尺度因子较为准确, 在进行后续操作时, 将这两个参数作为已知固定, 可以有效提高标定的准确性.

2.2 特征点映射

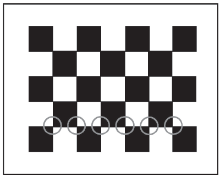
选用棋盘格为标定参照物, 可以清楚地确定空间物体表面某点的三维几何位置与其在图像中对应点之间的关系.图4为实验中使用的5× 7棋盘格, 每个棋盘格的大小为20 mm× 20 mm.

	Figure Option View Download New Window
	图4 棋盘格示意图Fig.4 Schematic diagram of checkerboard

如图4可知, 实际的棋盘格上, 同一行或者同一列的特征点是处于一条直线上的.由于鱼眼镜头采集的图像存在桶形畸变, 图像会出现外凸状况, 直线也会因此弯曲, 如图5所示.对鱼眼相机进行标定时, 如果标定结果精确度较高, 则在校正图中, 同一行及同一列的特征点, 仍应位于同一条直线上.本文算法中, 利用这一现象, 根据校正后特征点是否仍在一条直线上作为判定标准来衡量标定结果的精度, 进而确定光心.具体操作如下:

1)建立一个容器(其数据类型为点的横、纵坐标值).采集原图中棋盘格的特征点, 将这些特征点的像素坐标值依次存入该容器, 以便后续相关操作.

2)对这些点进行映射处理, 利用线性插值法, 将原图中每一个点到光心的距离对应到校正图的距离中, 舍去映射后不在图像范围内的点, 将满足要求的特征点在校正图中的像素坐标保存在容器中.为便于理解, 给出伪代码如下:

If OrgMaxPointDis< OrgMaxDis

Return xBar, yBar

Else

Return Error

If xBar< 0||yBar< 0||Bar> Wbar||yBar> Hbar

Return Error

Else

Return OK

其中:OrgMaxPointDis为原图中的点到光心的距离; OrgMaxDis为原图中距离光心的最大距离; xBar为校正图中点的横坐标; yBar为校正图中点的纵坐标; Wbar为校正图的宽度; Hbar为校正图的高度.

	Figure Option View Download New Window
	图5 鱼眼镜头畸变图像Fig.5 Distortion image captured by fish-eye lens

2.3 直线拟合及光心坐标的确定

将上述得到校正后的2D或3D点集输入到直线拟合函数中, 不同的距离函数所对应的直线拟合方法也不一样.该函数的原理采用6种不同的距离函数, 如下式

$\begin{array}{l} ρ_{1} (r) = \frac{r^{2}}{2} (6) \\ ρ_{2} (r) = r (7) \\ ρ_{3} (r) = 2 (\sqrt[]{1 + \frac{r^{2}}{2}} - 1) (8) \\ ρ_{4} (r) = C_{1}^{2} [\frac{r}{C_{1}} - \log (1 + \frac{r}{C_{1}})] (9) \\ ρ_{5} (r) = \frac{C_{2}^{2}}{2} [1 - \exp (- {(\frac{r}{C_{2}})}^{2})] (10) \\ ρ_{6} (r) = \{\begin{array}{l} \frac{r^{2}}{2}, r < C_{3} \\ C_{3} (r - \frac{C_{3}}{2}), 其他 \end{array} (11) \end{array}$

式中: $C_{1} = 1.399 8; C_{2} = 2.984 6; C_{3} = 1.345$ ; $r$ 表示点 $(x_{i}, y_{i})$ 到拟合直线的距离如下

$D = \arg \min_{D} sum : ρ_{i} (r) (12)$

通过计算, 找到使 $D$ 值最小的距离函数 $ρ_{\min}$ , 用该距离函数对应拟合出一条直线, 返回该直线的单位向量和线上某个点.利用返回值可以求得拟合直线的一般式 $Ax + By + C = 0$ 中 $A 、 B 、 C$ 3个参数并确定对应直线.将 $A 、 B 、 C$ 和校正图中特征点集作为参数输入算法程序, 计算点到直线距离采用的公式如下

$d = \frac{Ax + By + C}{\sqrt[]{A^{2} + B^{2}}} (13)$

原图经过畸变校正以后, 不同光心对应的距离和之间差异可能很微弱, 为了提高算法的稳定性和健全性, 对不同的点赋予不同的权重, 来扩大不同光心坐标所对应距离和之间的差异.

如图6所示, 位于同一行的6个特征点, 设它们到对应拟合直线的距离从左至右依次为 $d_{1} 、 d_{2} 、 d_{3} 、 d_{4} 、 d_{5} 、 d_{6}$ .根据鱼眼镜头的成像规律可知, 越接近图像边缘时, 图像的畸变越大, 因此, 给这6个特征点分别赋予权值 $μ_{1} 、 μ_{2} 、 μ_{3} 、 μ_{4} 、 μ_{5} 、 μ_{6}$ (一般情况下, 越接近边缘的点权值越高), 再求出点到拟合直线的加权距离

$\begin{array}{l} L = μ_{1} d_{1} + μ_{2} d_{2} + μ_{3} d_{3} + \\ μ_{4} d_{4} + μ_{5} d_{5} + μ_{6} d_{6} (14) \end{array}$

用校正图中所有特征点到对应拟合直线的加权距离和作为评判该光心坐标精准度的标准.

在2.1节中, 已将求得的内参矩阵中水平轴的尺度因子 $f_{x}$ 和垂直轴的尺度因子 $f_{y}$ 固定.便可对光心的横、纵坐标进行遍历操作, 通过比较, 求得使所有校正后特征点到对应拟合直线加权距离和最小的光心, 即在该光心坐标下, 标定板上原处于同一条线上的特征点在畸变校正后更接近于同一条直线.这样得到的畸变校正效果较好, 提高了参数和相机标定的精确性.

	Figure Option View Download New Window
	图6 权值示意图Fig.6 A weight sketch map

3 实验结果与分析

为验证本文算法的有效性, 实验部分选择5组图片分析该种相机标定算法的精确性, 同时对得出的数据进行图像化处理, 以便清晰直观地得出结论.

选择第1组图片的图像处理结果进行说明.第1组图片光心的参考坐标为(350, 277), 预先给定的遍历范围是光心横纵坐标 $c_{x} 、 c_{y}$ 正负各20个像素值.实验输出每一个光心的编号和坐标( $c_{x}, c_{y}$ )及对应的特征点到拟合直线的加权距离和.实验结果如图7所示.

	Figure Option View Download New Window
	图7 实验结果Fig.7 Experiment results

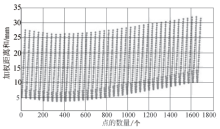
通过图7可以发现, 鱼眼相机采集得到的畸变图7(a)中, 标定板的方格线已经明显发生了弯曲.传统算法的校正图7(b)虽然在很大程度上校正了畸变, 但是圆圈标示的地方还是有轻微的弯曲, 而用本文算法进行标定后的图7(c)中, 取得了较好的效果, 各行、各列的特征点均回归于同一直线.利用输出的结果绘制散点图, 如图8所示.

	Figure Option View Download New Window
	图8 散点图Fig.8 Scatter diagram

在实验中, 将光心的横坐标固定, 对光心的纵坐标进行正负20个像素点的遍历, 对应每一个光心横坐标 $c_{x}$ , 即可得到如图8所示的多个散点组成的平滑曲线, 且每一个光心的横坐标的值对应一个最小的加权距离和, 即为散点图中每一条平滑曲线的最低点, 即在该光心横坐标下, 使得畸变校正结果最好的点.将这些点输出的编号、坐标和距离值整合得到表1.

首先对表1中的数据进行纵向比较, 当光心纵坐标为274时, 使得每一个光心横坐标下, 特征点到拟合直线的加权距离和最小, 即校正的结果最好.再进行横向比较, 即当光心纵坐标为274时, 比较所有的光心横坐标, 找到其中特征点到拟合直线加权距离最小的点, 即为最终所求的校正效果最优的光心.本实验中, 最终得到的校正效果最优的光心坐标为(348, 274), 与参考值(350, 277)非常接近.

表1 加权距离和最小的光心坐标值 Tab.1 Minimum weighted distance and the corresponding optic center coordinate

同理, 实验其他4组图片, 得到表2数据.

表2 光心坐标值对比分析 Tab.2 Contrast analysis diagram of optic center coordinate

本文算法校正后的图像, 计算光心和参考光心的误差明显减小, x方向的误差约为2个像素值, y方向的误差约为3个像素值.

为了进一步验证本文算法的有效性, 将实验结果和传统的相机标定算法进行比较(传统相机标定的数据由经典相机标定工具箱得到^[16], 特征点采集时可能存在少许误差).对比数据如表3所示.

表3 本文算法和传统算法比较 Tab.3 Comparison between the proposed algorithm and traditional algorithm

通过表3光心坐标算法得到误差的分析见表4.通过对比, 可以清楚地得到, 本文的算法相比传统算法有了很大地改善, 算法所得光心的横纵坐标的像素差值较传统算法有3~5个像素值的优化.充分证明了本文算法的有效性, 这样所得的标定结果将会更加精确.

表4 据表3的误差分析 Tab.4 Error analysis according to Tab.3

4 结论

1)通过对比光心坐标的参考值可以发现, 本文算法所得的光心坐标值更加精确.

2)本文算法计算的结果较基于小孔成像的传统算法存在明显的优化, 将内参矩阵中光心参数的误差减小至0.7%, 提高了相机标定的准确度.

3)本文算法简单高效, 仅使用单幅图像即可完成光心坐标的确定及后续的相机标定, 可满足对实时性要求较高的场景, 具有很好的实用性.

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	佟帅, 徐晓刚, 易成涛, 等. 基于视觉的三维重建技术综述[J]. 计算机应用研究, 2011, 28(7): 2411-2417. TONG Shuai, XU Xiaogang, YI Chengtao, et al. Overview on vision-based 3D reconstruction[J]. Application Research of Computers, 2011, 28(7): 2411-2417. (in Chinese) [本文引用:1]
[2]	KANG H, WANG M Q, WANG Y Y. Three-dimensional image reconstruction technique[J]. Technological Development of Enterprise, 2009, 28(6): 42-43. [本文引用:1]
[3]	ABRAHAM S, FÖRSTNER W. Fish-eye-stereo calibration and epipolar rectification[J]. ISPRS Journal of Photogrammetry & Remote Sensing, 2005, 59(5): 278-288. [本文引用:1]
[4]	LIU H J, CHEN C, MIAO L G, et al. Study of key technology of distortion correction software for fisheye image[J]. Instrument Technique & Sensor, 2011, 40(7): 100-152. [本文引用:1]
[5]	吴开兴, 段马丽. 新的桶形畸变的点阵样板校正方法[J]. 计算机应用, 2012, 32(4): 1113-1115. WU Kaixing, DUAN Mali. New method of correcting barrel distortion on lattice model[J]. Journal of Computer Applications, 2012, 32(4): 1113-1115. (in Chinese) [本文引用:1]
[6]	WANG Z, LEI Y, ZHANG Z, et al. Research on measurement and correction of a fish-eye image distortion[C]. International Symposium on Advanced Optical Manufacturing and Testing Technologies, 2014: 928214. [本文引用:1]
[7]	林颖, 龚小谨, 刘济林. 基于单位视球的鱼眼相机标定方法[J]. 浙江大学学报(工学版), 2013, 47(8): 1500-1507. LIN Ying, GONG Xiaojin, LIU Jilin. Calibration of fisheye cameras based on the viewing sphere[J]. Journal of Zhejiang University(Engineering Science), 2013, 47(8): 1500-1507. (in Chinese) [本文引用:1]
[8]	XIONG Y, TURKOWSKI K. Creating image-based VR using a self-calibrating fisheye lens[C]. Conference on Computer Vision and Pattern Recognition, 1997: 237-243. [本文引用:1]
[9]	周飚, 赵鑫, 齐志宏, 等. 一种通用的基于抛物面模型的鱼眼图像校正算法[J]. 长春理工大学学报(自然科学版), 2014, 37(2): 22-25. ZHOU Biao, ZHAO Xin, QI Zhihong, et al. A common fisheye correction algorithm based on paraboloidal model[J]. Journal of Changchun University of Science and Technology (Natural Science Edition), 2014, 37(2): 22-25. (in Chinese) [本文引用:1]
[10]	HUGHES C, DENNY P, JONS E. Accuracy of fish-eye lens models[J]. Applied Optics, 2010, 49(17): 3338-3347. [本文引用:1]
[11]	黄岩岩, 李庆, 张斌珍. 鱼眼畸变棋盘格图像校正[J]. 计算机工程与应用, 2014, 50(12): 111-114. HUANG Yanyan, LI Qing, ZHANG Binzhen. Fisheye distortion chessboard images correction[J]. Computer Engineering & Applications, 2014, 50(12): 111-114. (in Chinese) [本文引用:1]
[12]	GONZALEZ R C, WOODS R E. Digital image processing[M]. Boston: Addison-Wesley, 2010. [本文引用:1]
[13]	YOSHIKAWA N. Spatial position detection of three-dimensional object using complex amplitude derived from Fourier transform profilometry[J]. Optical Review, 2005, 12(5): 378-382. [本文引用:1]
[14]	XIA Q, TAN S R, LOU J T, et al. A three-point calibration method for fish-eye camera equivalent focal length[J]. Journal of Optoelectronics Laser, 2013, 24(6): 1133-1137. [本文引用:1]
[15]	BO T U, LIU L, LIU Y H, et al. A calibration method for fish-eye cameras based on pinhole model[J]. Acta Automatic Sinica, 2014, 40(4): 653-659. [本文引用:1]
[16]	ZHANG Z. Flexible camera calibration by viewing a plane from unknown orientations[C]. IEEE International Conference on Computer Vision, 1999, 1: 666. [本文引用:1]

2011

0.0

佟帅, 徐晓刚, 易成涛, 等. 基于视觉的三维重建技术综述[J]. 计算机应用研究, 2011, 28(7): 2411-2417.

TONG

Shuai

, XU

Xiaogang

, YI

Chengtao

, et al. Overview on vision-based 3D reconstruction[J]. Application Research of Computers, 2011, 28(7): 2411-2417. (in Chinese)

摘　要：基于视觉的三维重建仍然存在较大局限性。通过介绍基于视觉的三维重建技术的主要方法及其研究现状，对各种方法优缺点进行了比较分析，期望能够对该领域有较全面的把握，进一步明确未来的研究方向。

... 同时,随着计算机软硬件技术的持续发展,三维重建技术^[1,2]成为数字媒体、科学计算、医学图像处理、计算机视觉等领域的共性科学问题和核心技术 ...

2009

0.0

2005

0.0

... 为满足该技术对模型的复杂度和真实度的要求,研究者将具有优良特性的鱼眼相机和三维重建技术相结合来进行深度恢复和全景漫游^[3],应用于虚拟现实、行车安全及视觉监控等领域^[4] ...

2011

0.0

2012

0.0

吴开兴, 段马丽. 新的桶形畸变的点阵样板校正方法[J]. 计算机应用, 2012, 32(4): 1113-1115.

Kaixing

, DUAN

Mali

. New method of correcting barrel distortion on lattice model[J]. Journal of Computer Applications, 2012, 32(4): 1113-1115. (in Chinese)

... 虽然鱼眼镜头可以获得很大的视角,但是根据物理成像的规律,焦距越短,视角越大,所以,鱼眼相机采集的图像通常都引入了桶形畸变^[5],所成的图像除了光心四周基本不变外,其他图像区域都存在一定程度上的畸变^[6],图像不易被理解 ...

2014

0.0

2013

0.0

林颖, 龚小谨, 刘济林. 基于单位视球的鱼眼相机标定方法[J]. 浙江大学学报(工学版), 2013, 47(8): 1500-1507.

LIN

Ying

, GONG

Xiaojin

, LIU

Jilin

. Calibration of fisheye cameras based on the viewing sphere[J]. Journal of Zhejiang University(Engineering Science), 2013, 47(8): 1500-1507. (in Chinese)

With respect to the large field of view (FOV) of a fisheye camera, a new calibration method was proposed, This method takes advantage of two mutually orthogonal sets of parallel lines. The intrinsic parameters could be initialized by the field of view (FOV) and imaging boundary, and corners extracted in the image plane could be back-projected to a viewing sphere. Two geometric properties of the two line sets on the viewing sphere provided a closed-form solution for extrinsic parameters. Finally, all the parameters were optimized according to the re-projection errors of the corners. Three commonly used fisheye projection models are simulated with respect to the image number and noise level. The simulation shows that, within meaningful noise, the method can achieve high accuracy when the image number is larger than 5. A fisheye camera with 185°FOV is also calibrated, and a geometry-known trihedral object is further tested to validate the estimation of extrinsic parameters. The experiments compared to the popular fisheye calibration toolbox from Caltech prove that with a lower uncertainty, the proposed method is more accurate than Caltech’s toolbox.

针对鱼眼镜头的大范围视场,提出一种新的鱼眼相机标定方法.利用2组相互垂直的平行线来进行鱼眼相机标定.依据相机视场和成像边缘得到内部参数的估计值后,将图像平面上提取的角点反投影到单位视球（viewing sphere）上,2组平行线在单位球面上的2种几何特性提供外部参数估计的解析解.利用角点在图像平面的重投影误差来,得到优化后的所有参数.对3种常见的鱼眼投影模型分别进行关于标定图像数量和噪声水平的仿真实验.从仿真结果来看,在合理的噪声范围内,当用于标定的图像大于5张时,可以得到精度较高的标定结果.利用视场角185°的鱼眼相机来进行标定,并进一步的利用已知结构的立方体模板来验证外参估计方法.与加州理工学院提供的标定工具箱相比较，结果表明该算法不确定度较低,提供更为准确的标定结果.

... 因此,该方法不能运用于行车安全和监控等对实时性要求很高的领域,并且,当光心坐标的求解不够精确时,将会产生误差的累积,影响整个标定的精确性^[7] ...

1997

0.0

... 文献[8]提出了一种鱼眼标定方法,但该方法仅考虑了径向变形而没有考虑到切向变形等因素,得到的标定参数精度较低,无法应用于一些精度要求高的标定场合 ...

2014

0.0

周飚, 赵鑫, 齐志宏, 等. 一种通用的基于抛物面模型的鱼眼图像校正算法[J]. 长春理工大学学报(自然科学版), 2014, 37(2): 22-25.

ZHOU

Biao

, ZHAO

Xin

, QI

Zhihong

, et al. A common fisheye correction algorithm based on paraboloidal model[J]. Journal of Changchun University of Science and Technology (Natural Science Edition), 2014, 37(2): 22-25. (in Chinese)

摘　要：鱼眼镜头具有较大的视场，但所拍摄图像会产生严重的桶形畸变，使用时需要进行校正。提出一种新的基于抛物面的透视投影模型，分析了此模型下图像的投影特征及抛物面参数对校正效果的影响，利用鱼眼图像中的特征点拟合出抛物面的最佳参数值，最后通过拟合后的抛物面模型将鱼眼图像映射成透视投影图像，实现了对鱼眼镜头畸变的校正。实验表明，与传统的球面投影模型相比，该模型有更好的校正质量。

... 文献[9]提出一种通用的基于抛物面模型的鱼眼图像校正算法,对鱼眼图像中代表空间水平或竖直直线的曲线进行了采样,并拟合出抛物面的直线,但是根据文献的实验结果来看,该方法并没有很好地复原弯曲的直线,校正效果不够精确 ...

2010

0.0

... 文献[10]提出了平面校正方法,该方法校正的缺点是比较受视野大小的局限^[11] ...

2014

0.0

黄岩岩, 李庆, 张斌珍. 鱼眼畸变棋盘格图像校正[J]. 计算机工程与应用, 2014, 50(12): 111-114.

HUANG

Yanyan

, LI

Qing

, ZHANG

Binzhen

. Fisheye distortion chessboard images correction[J]. Computer Engineering & Applications, 2014, 50(12): 111-114. (in Chinese)

Distorted checkboard image can more accurately describe the characteristics of the fisheye lens distortion, so the study of distorted checkboard image correction algorithm is importent to correct the distorted image accurately and efficiently. Based on the reaserch of correction algorithm by Carroll et al, a simple and fast calibration method is proposed for distorted checkboard images. Instead of line feature as the input of model, corners of the checkboard are preferred. Then the objective function is optimized using linear system. In this way, distortion can be achieved automation, as well as the efficiency. Experiments results show that the method is convenient and practical, and the result of correction is well, too.

畸变棋盘格图像能够更精确地描述鱼眼镜头的畸变特征，畸变棋盘格图像校正算法的研究对实现畸变图像准确快捷的校正具有重要意义。在研究Carroll等人提出的校正方法的基础上，针对畸变的棋盘格图像提出了一种简单、快捷的校正方法。以棋盘格的角点坐标替代直线特征信息作为校正模型的输入，对建模后的目标函数进行线性优化求解。该方法实现了畸变校正的自动化，提高了系统的效率。实验表明，该方法方便可行，校正结果良好。

... 文献[10]提出了平面校正方法,该方法校正的缺点是比较受视野大小的局限^[11] ...

2010

0.0

... 1 理想的相机成像原理相机拍摄图像的过程,实际上是一个光学成像的过程,其中涉及到4个坐标系:世界坐标系、相机坐标系、图像坐标系和像素坐标系^[12] ...

2005

0.0

... 4个坐标系之间的关系如图1所示^[13] ...

2013

0.0

... t是一个三维的平移向量^[14] ...

2014

0.0

... 由于工艺限制,以及后期镜头座的安装等问题,经常造成镜头光心不准确,如果将光心坐标直接作为参数代入到内参矩阵中进行后续使用,就会存在累积误差,从而大大影响随后相机的标定及畸变校正的精确性^[15] ...

1999

0.0

... 为了进一步验证本文算法的有效性,将实验结果和传统的相机标定算法进行比较(传统相机标定的数据由经典相机标定工具箱得到^[16],特征点采集时可能存在少许误差) ...