一种可重构空间四杆机构

引用本文

王冰, 方跃法, 房海蓉. 一种可重构空间四杆机构[J]. 北京交通大学学报, 2017,41(1): 107-113.
WANG Bing, FANG Yuefa, FANG Hairong. A reconfigurable spatial four-bar mechanism[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2017,41(1): 107-113.
Doi:10.11860/j.issn.1673-0291.2017.01.017 复制到剪切板

Permissions

北京交通大学学报编辑部所有

一种可重构空间四杆机构

王冰^1,², 方跃法¹, 房海蓉¹

1.北京交通大学机械与电子控制工程学院,北京 100044

2.北华航天工业学院机电工程学院,河北廊坊 065000

通讯作者:方跃法(1958—),男,安徽绩溪人,教授,博士,博士生导师.email:yffang@bjtu.edu.cn

第一作者:王冰(1976—),男,黑龙江齐齐哈尔人,副教授,博士生.研究方向为机构学.email: 13116337@bjtu.edu.cn

收稿日期: 2016-09-18

基金: 国家自然科学基金资助项目(51675037)

摘要

提出一种可重构空间四杆机构,其具有两种不同的工作模式,模式Ⅰ为一个转动运动,模式Ⅱ为一个平移平动,两种运动模式进行切换的初始位形具有瞬时的一个转动和一个平动.将可重构空间四杆机构与一个具有两移动和两转动的串联支链相连,构成一种具有两种不同工作模式的可重构混联支链.利用3条可重构混联支链连接并联机构的固定平台和运动平台,可得到一种新型可重构并联机构,通过控制3条可重构混联支链分别在两种不同工作模式间切换,可重构并联机构可实现4种不同的三自由度运动模式.利用螺旋理论分析和证明了上述结论.

关键词: 自由度; 可重构机构; 螺旋理论

中图分类号:TH112 文献标志码:A

A reconfigurable spatial four-bar mechanism

WANG Bing^1,², FANG Yuefa¹, FANG Hairong¹

1.School of Mechanical, Electronic and Control Engineering, Beijing Jiaotong University, Beijing 100044,China

2. School of Mechanical and Electrical Engineering, North China Institute of Aerospace Engineering, Langfang Hebei 065000, China

Fund:National Natural Science Foundation of China(51675037)

Abstract

A reconfigurable spatial four-bar mechanism with two different operation modes is proposed. The mechanism has one rotational motion mode, one translational motion mode, one rotational and translational motions mode in the initial configuration where the mechanism can transit from one operation mode to another, respectively. Reconfigurable hybrid chain with two distinct phases is obtained by integrating the reconfigurable spatial four-bar mechanism with serial limb that has two translational and two rotational motions. A new kind of reconfigurable parallel mechanism is constructed with three identical hybrid chains connecting the fixed base and the moving platform. By controlling the three hybrid chains move into different motion modes, the reconfigurable parallel mechanism has the ability to perform four kinds of motion with three degree of freedom(DOF). The special mobility of the mechanisms are analyzed and proved by using the screw theory.

Keyword: degree of freedom; reconfigurable mechanism; screw theory

文章图片

可重构并联机构因即具有并联机构承载能力强、刚度高、动态特性好的优点, 同时又具有可重构机构适应性强和快速可变结构特性, 其吸引了机构学研究者的广泛兴趣.在这种背景下, 学者们提出了许多特色鲜明的可重构并联机构, 按其可重构原理, 可将可重构并联机构分为利用约束奇异实现可重构的并联机构和变胞并联机构两大类.

第1类可重构并联机构的重构过程发生在机构的约束奇异位置, 如KONG等提出的多模式并联机构^{[1, 2]}; 李秦川等提出的变自由度并联机构^[3]和可实现Schoenflies运动的并联机构^[4]; YE和FANG等将约束奇异由并联机构支链间转移至支链内部, 即通过闭链的约束奇异实现混联支链的重构, 提出了一类可重构并联机构构型综合的新方法, 综合出一系列含约束奇异特性单环闭链的可重构并联机构^{[5, 6, 7]}.

第2类可重构并联机构为变胞并联机构, 其可重构原理是机构在连续运动过程中由于运动副类型变化或有效杆件数目变化使得并联机构的拓扑结构发生变化, 进而导致并联机构自由度的变化.GAN等提出一种轴线位置可变的rR运动副(可重构转动副), 利用该变胞运动副设计了一种可实现纯三维转动运动模式和一移二转运动模式切换的3rRPS(P代表移动副; S代表球副)变胞并联机构^[8]; GAN等提出一种具有两种不同子构态的rT变胞运动副(可重构虎克铰链), 该变胞运动副可在虎克铰和转动副之间切换, 利用该变胞运动副构型了一类变胞并联机构, 并利用螺旋理论对其自由度进行了分析^[9]; ZHANG等提出一种具有3种不同子构态的vA运动副(变轴线关节), 该变胞运动副可实现球副、虎克铰和转动副3种不同子构态的切换, 利用螺旋理论分析了vA运动副构态变化机理, 并利用该变胞运动副构型了一类3S_vPS_v(S_v为可重构球副)变胞并联机构^[10]; YE和FANG利用闭链机构的支链奇异特性, 将具有3种不同子构态的平面五杆机构与串联支链混联构造可重构混联支链, 应用螺旋理论构型出可实现10种不同运动模式的可重构并联机构^[11].

由上述分析可见, 可重构并联机构的重构位置一般发生在机构的约束奇异位置或者机构的支链奇异位置, 为避免机构在重构时经过上述奇异位置, KONG等利用关节锁死的方法, 综合了一种三自由度多操作模式并联机构^[12].由于机构变胞过程中的杆件重合与合并实质上可以认为与关节的锁死是等效的, 这类机构实质上也可以认为是变胞并联机构.

根据上述分析可以发现, 现有的可重构并联机构仍然比较少, 可重构并联机构的设计往往依赖于设计者的灵感, 设计者巧妙地将变胞运动副、可锁死关节、可重构运动平台^[12]、运动分叉单环闭链^[13]及平面变胞机构等引入并联机构设计进而实现并联机构的可重构.

空间四杆机构可以视为一种广义并联机构, 不同于文献[13]所提出的可重构单环闭链机构, 将二自由度球面五杆机构引入到可重构并联机构设计, 用其替代了文献[13]中的1个虎克铰链, 利用球面二自由度五杆机构实现机构整体的二自由度并联驱动输入, 得到一种可重构空间四杆机构, 利用螺旋理论对其自由度特性进行了分析.该可重构四杆机构可作为运动分叉单环闭链应用于多自由度可重构并联机构设计; 用相同的方法, 用球面五杆机构和虎克铰链替代其他平面并联机构的两个平面运动副, 可得到其他具有运动分叉特性的单环或多环闭链机构.

1 可重构四杆机构

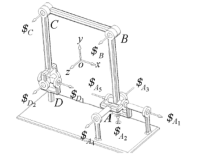
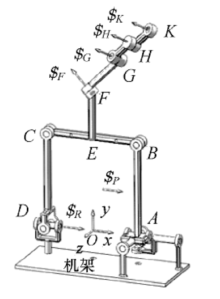
初始位形下的可重构空间四杆机构如图1所示, 该空间四杆机构含机架AD、连杆BC、连架杆AB和CD四根杆, 在不失一般性的前提下, 这里取四根杆的杆长相等且为r.在初始位形下, 连架杆与机架垂直, 连杆与机架平行.该空间四杆机构含两个平面运动副和两个空间运动副, 连杆BC与连架杆AB在B点通过转动副相连, 连杆BC与连架杆CD在C点也通过转动副相连, 连架杆CD与机架AD在D点通过虎克铰相连, 连架杆AB与机架AD通过一个二自由度球面五杆机构相连.

	Figure Option View Download New Window
	图1 可重构空间四杆机构Fig.1 A reconfigurable spatial four-bar mechanism

在图1和图2中各运动副处的单向箭头代表空间四杆机构的运动副螺旋, 建立机构固定坐标O-xyz如图1中所示, 这里选取固定坐标系的坐标原点O点与二自由度球面五杆机构的转动中心A点重合, 为视图方便, 在图1及后续视图中将固定坐标系O-xyz浮动到某一方便位置, 但坐标系方向未变.运动副螺旋 $$_{A_{4}}$ 、$_B、$_C和 $$_{D_{2}}$ 的轴线相平行; $$_{A_{1}}$ 与 $$_{D_{1}}$ 轴线方向一致; $$_{A_{1}}$ 与 $$_{A_{2}}$ 、 $$_{A_{3}}$ 与 $$_{A_{5}}$ 、 $$_{A_{4}}$ 与 $$_{A_{5}}$ 分别正交, 且 $$_{A_{1}}$ 、 $$_{A_{2}}$ 、 $$_{A_{3}}$ 、 $$_{A_{4}}$ 和 $$_{A_{5}}$ 轴线汇交于A点; $$_{D_{1}}$ 与 $$_{D_{2}}$ 正交于D点.

	Figure Option View Download New Window
	图2 二自由度球面五杆机构Fig.2 2-DOF spherical five bar mechanism

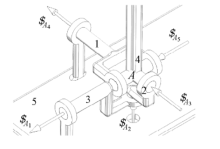
这里球面五杆机构可视为一广义运动副, 将图1中A点局部放大可得球面五杆机构的放大视图如图2所示, 其含5根连杆和5个转动副, 各连杆间都通过转动副相连接, 各转动副的轴线都通过同一个转动中心A点, 所有构件上所有的点的轨迹都是以A点为中心的球面曲线.图2中, 构件1和构件3为驱动杆, 构件5为机架, 构件2为中间连杆, 构件4为二自由度球面五杆机构的输出构件, 即为图1中的连架杆AB.这里球面五杆机构可视为一个能实现二自由度并联输入的广义运动副.

2 可重构四杆机构的自由度

2.1 初始位形下的自由度

初始位形下的可重构空间四杆机构如图1所示, 设球面五杆机构驱动杆1和3的转角分别为α 和β , 此时α =β =0.选取连杆AB作为空间四杆机构的运动平台, 则固定平台通过3条支链与运动平台相连. $$_{A_{1}}$ 、 $$_{A_{2}}$ 和 $$_{A_{3}}$ 组成支链1, $$_{A_{4}}$ 和 $$_{A_{5}}$ 组成支链2, $$_{D_{1}}$ 、 $$_{D_{2}}$ 、$_C和$_B组成支链3.支链1的运动螺旋系为

$\{\begin{array}{l} $_{A_{1}} = (\begin{array}{l} 1 & 0 & 0; & 0 & 0 & 0 \end{array}) \\ $_{A_{2}} = (\begin{array}{l} 0 & 1 & 0; & 0 & 0 & 0 \end{array}) \\ $_{A_{3}} = (\begin{array}{l} \begin{array}{l} 0 & 0 & 1 \end{array}; & 0 & 0 & 0 \end{array}) \end{array} (1)$

对式(1)取反螺旋可得支链1的约束螺旋系为

$\{\begin{array}{l} $_{11}^{r} = (\begin{array}{l} 1 & 0 & 0; & 0 & 0 & 0 \end{array}) \\ $_{12}^{r} = (\begin{array}{l} 0 & 1 & 0; & 0 & 0 & 0 \end{array}) \\ $_{13}^{r} = (\begin{array}{l} \begin{array}{l} 0 & 0 & 1 \end{array}; & 0 & 0 & 0 \end{array}) \end{array} (2)$

式(2)表明在初始位形下, 支链1对运动平台施加3个分别沿x、y、z坐标方向的约束力矢.支链2的运动螺旋系为

$\{\begin{array}{l} $_{A_{4}} = (\begin{array}{l} 0 & 0 & 1; & 0 & 0 & 0 \end{array}) \\ $_{A_{5}} = (\begin{array}{l} 1 & 0 & 0; & 0 & 0 & 0 \end{array}) \end{array} (3)$

对式(3)取反螺旋可得支链2的约束螺旋系为

$\{\begin{array}{l} $_{21}^{r} = (\begin{array}{l} 1 & 0 & 0; & 0 & 0 & 0 \end{array}) \\ $_{22}^{r} = (\begin{array}{l} 0 & 1 & 0; & 0 & 0 & 0 \end{array}) \\ $_{23}^{r} = (\begin{array}{l} \begin{array}{l} 0 & 0 & 1 \end{array}; & 0 & 0 & 0 \end{array}) \\ $_{24}^{r} = (\begin{array}{l} \begin{array}{l} 0 & 0 & 0 \end{array}; & 0 & 1 & 0 \end{array}) \end{array} (4)$

式(4)表明在初始位形下, 支链2对运动平台施加4个约束, 分别是沿x、y、z3个坐标方向的约束力矢和一个沿y轴方向的约束力耦.支链3的运动螺旋系为

$\{\begin{array}{l} $_{D_{1}} = (\begin{array}{l} 1 & 0 & 0; & 0 & 0 & 0 \end{array}) \\ $_{D_{2}} = (\begin{array}{l} 0 & 0 & 1; & 0 & r & 0 \end{array}) \\ $_{C} = (\begin{array}{l} \begin{array}{l} 0 & 0 & 1 \end{array}; & r & r & 0 \end{array}) \\ $_{B} = (\begin{array}{l} \begin{array}{l} 0 & 0 & 1 \end{array}; & r & 0 & 0 \end{array}) \end{array} (5)$

对式(5)取反螺旋可得支链3的约束螺旋系为

$\{\begin{array}{l} $_{31}^{r} = (\begin{array}{l} 0 & 0 & 1; & 0 & 0 & 0 \end{array}) \\ $_{32}^{r} = (\begin{array}{l} 0 & 0 & 0; & 0 & 1 & 0 \end{array}) \end{array} (6)$

式(6)表明在初始位形下, 支链3对运动平台施加2个约束, 分别是沿z轴方向的约束力矢和沿y轴方向的约束力耦.由3条支链的约束螺旋系式(2)、式(4)和式(6)可得空间四杆机构在初始位形下的公共约束为

$$_{0}^{r} = (\begin{array}{l} 0 & 0 & 1; & 0 & 0 & 0 \end{array}) (7)$

因此, 此位形下机构的公共约束数λ =1, 机构的阶数d=6-λ =5.除去公共约束剩余6个反螺旋组成一个3系螺旋, 所以初始位形下机构的并联冗余约束数为v=6-3=3, 由修正的G-K公式^[14]可得在初始位形下机构的自由度为

$\begin{array}{l} M = d (n - g - 1) + \overset{g}{\sum_{i = 1}} f_{i} + v \\ = 5 (7 - 8 - 1) + 9 + 3 = 2 \end{array} (8)$

式中:n为机构中包含机架在内总的构件数; g为运动副的数目; f_i为第i个运动副的自由度数.

对于杆AB, 式(2)、式(4)和式(6)即为施加在其上的约束螺旋, 对上述3个等式取二次反螺旋, 可得杆AB的运动螺旋系为

$[\begin{array}{l} 1 & 0 & 0; & 0 & 0 & 0 \\ 0 & 0 & 1; & 0 & 0 & 0 \end{array}] .$

可见在初始位形下, 连架杆AB的瞬时自由度数为2, 且自由度的性质为绕x轴和z轴的二维瞬时旋转.因连架杆DC与AB平行, 所以杆DC与AB具有相同的自由度性质.

同理, 对于连杆BC, 如视其为机构的运动平台, 则 $$_{D_{1}}$ 、 $$_{D_{2}}$ 、$_C组成支链1、 $$_{A_{1}}$ 、 $$_{A_{2}}$ 、 $$_{A_{3}}$ 、 $$_{A_{4}}$ 、 $$_{A_{5}}$ 和$_B组成支链2, 各运动副的运动螺旋已在式(1)、式(3)和式(5)中列出, 对两个支链的运动螺旋系取反螺旋可得连杆BC由独立约束螺旋组成的约束螺旋系为

$[\begin{array}{l} 0 & 1 & 0; & 0 & 0 & 0 \\ 0 & 0 & 1; & 0 & 0 & 0 \\ 0 & 0 & 0; & 0 & 1 & 0 \\ 0 & 0 & 0; & 0 & 0 & 1 \end{array}] .$

对其取二次反螺旋可得连杆BC的运动螺旋系为

$[\begin{array}{l} 1 & 0 & 0; & 0 & 0 & 0 \\ 0 & 0 & 0; & 1 & 0 & 0 \end{array}] .$

可知在初始位形下连杆BC的自由度数为2, 自由度性质为绕x轴的瞬时转动和沿x轴的瞬时移动.

2.2 一般位形下的自由度

在一般位形下, 假设球面五杆机构的驱动杆1和3分别转动α 和β , 将连杆AB作为输出构件.支链1的运动螺旋系为

$\begin{array}{l} \{\begin{array}{l} $_{A_{1}} = (\begin{array}{l} 1 & 0 & 0; & 0 & 0 & 0 \end{array}) \\ $_{A_{2}} = (\begin{array}{l} 0 & c β & s β; & 0 & 0 & 0 \end{array}) \\ $_{A_{3}} = (\begin{array}{l} s_{A_{3}}; & 0 & 0 & 0 \end{array}) \end{array} (9) \\ s_{A_{3}} = \frac{s_{A_{5}} \times s_{A_{2}}}{‖ s_{A_{5}} \times s_{A_{2}} ‖} = \frac{1}{Δ} (\begin{array}{l} s α s β & - c α s β & c α c β \end{array}) (10) \end{array}$

式中:s和c分别代表sin和cos运算.

$Δ = ‖ s_{A_{5}} \times s_{A_{2}} ‖ = \sqrt[]{s^{2} β + c^{2} α c^{2} β} (11)$

对式(9)取反螺旋, 可得到支链1的约束螺旋系为

$\{\begin{array}{l} $_{11}^{r} = (\begin{array}{l} 1 & 0 & 0; & 0 & 0 & 0 \end{array}) \\ $_{12}^{r} = (\begin{array}{l} 0 & 1 & 0; & 0 & 0 & 0 \end{array}) \\ $_{13}^{r} = (\begin{array}{l} 0 & 0 & 1; & 0 & 0 & 0 \end{array}) \end{array} (12)$

这3个约束螺旋分别是沿x、y、z3个坐标方向的约束力矢. $$_{A_{4}}$ 和 $$_{A_{5}}$ 构成了支链2, 其运动螺旋系为

$\{\begin{array}{l} $_{A_{4}} = (\begin{array}{l} 0 & 0 & 1; & 0 & 0 & 0 \end{array}) \\ $_{A_{5}} = (\begin{array}{l} c α & s α & 0; & 0 & 0 & 0 \end{array}) \end{array} (13)$

对式(13)求反螺旋可得支链2的约束螺旋系为

支链3的运动螺旋系为

$\{\begin{array}{l} $_{D_{1}} = (\begin{array}{l} \begin{array}{l} 1 & 0 & 0; \end{array} & 0 \end{array}) \\ $_{D_{2}} = (\begin{array}{l} s_{D_{2}}; & s_{D_{2}}^{0} \end{array}) \\ $_{C} = ({\begin{array}{l} s_{C}; & s \end{array}}_{C}^{0}) \\ $_{B} = (\begin{array}{l} s_{B}; & s_{B}^{0} \end{array}) \end{array} (15)$

其中

$\{\begin{array}{l} s_{D_{2}} = s_{C} = s_{B} = s_{A_{3}} \\ r_{D} = (\begin{array}{l} - r & 0 & 0 \end{array}), r_{C} = (\begin{array}{l} - r - r s α & r c α c β & r c α s β \end{array}) \\ s_{D_{2}}^{0} = r_{D} \times s_{D_{2}} = (\begin{array}{l} 0 & r c α c β / Δ & r c α s β / Δ \end{array}) \\ s_{B}^{0} = r_{B} \times s_{B} = r s_{AB} \times s_{B} = = (\begin{array}{l} r c α & r s α & 0 \end{array}) \\ s_{AB} = \frac{s_{A_{3}} \times s_{A_{5}}}{‖ s_{A_{3}} \times s_{A_{5}} ‖} = \frac{1}{Δ} (\begin{array}{l} - s α c α c β & c^{2} α c β & s β \end{array}) \\ s_{C}^{0} = r_{C} \times s_{C} = (\begin{array}{l} a & b & c \end{array}) \end{array} (16)$

式(16)中系数a、b和c为

$\{\begin{array}{l} a = r c^{2} α / Δ \\ b = r (s α c α s^{2} β + c α c β + s α c α c β) / Δ \\ c = r (c α s β + s α c α s β - s α c α s β c β) / Δ \end{array} (17)$

对式(15)取反螺旋可得支链3的约束螺旋系为

$\{\begin{array}{l} $_{31}^{r} = (\begin{array}{l} 0; & \begin{array}{l} 0 & c β & s β \end{array} \end{array}) \\ $_{32}^{r} = (\begin{array}{l} \begin{array}{l} s α s β & - c α s β & c α c β \end{array}; & 0 \end{array}) \end{array} (18)$

对比3条支链的约束螺旋系(12)、式(14)和式(18)可见在一般位形下机构的公共约束数λ =0, 则机构的阶数d=6-λ =6; 将式(12)、式(14)和式(18)的约束螺旋系合并并进行整理可得机构独立约束螺旋组成的约束螺旋系为

$[\begin{array}{l} 1 & 0 & 0; & 0 & 0 & 0 \\ 0 & 1 & 0; & 0 & 0 & 0 \\ 0 & 0 & 1; & 0 & 0 & 0 \\ 0 & 0 & 0; & - s α & c α & 0 \\ 0 & 0 & 0; & 0 & c β & s β \end{array}] .$

可见3条支链共提供9条线性相关的约束螺旋, 其秩为5, 因此可得机构的并联冗余约束数v=9-5=4, 机构在一般位形下的自由度为M=6(7-8-1)+9+4=1, 可见空间四杆机构在一般位形下自由度数为1.

求其二次反螺旋可得连架杆AB的运动螺旋为

$$_{AB} = (\begin{array}{l} \begin{array}{l} c α s β & s α s β & - s α c β; \end{array} & 0 \end{array}) (19)$

因在一般位形下机构的自由度为1, 所以应有α =0或β =0; 当α =0时

$$_{AB} = (\begin{array}{l} \begin{array}{l} 1 & 0 & 0; \end{array} & 0 \end{array}) (20)$

杆AB具有绕x轴转动的连续自由度; 当β =0时

$$_{AB} = (\begin{array}{l} \begin{array}{l} 0 & 0 & 1; \end{array} & 0 \end{array}) (21)$

杆AB具有绕z轴转动的连续自由度; 可见在一般位形下, 机构的连续自由度为1, 机构作两种性质不同的单自由度运动, 且这两种连续单自由度运动是互斥的, 运动的运动分叉位置即为机构的初始位形.

对于连杆BC, 当α =0时, Δ =1, $_AB= $(0 c β s β; 0)$ , $_B= $(0 - s β c β; r 00)$ , 设s_CB=(l m n), 因s_CB为单位矢量, 所以应满足

$l^{2} + m^{2} + n^{2} = 1 (22)$

对于矢量s_B、s_CB和s_AB应满足

$s_{B} = s_{CB} \times s_{AB} (23)$

联立式(22)和式(23)可解得s_CB=( $\begin{array}{l} 1 & 0 & 0 \end{array}$ ), $s_{CB}^{0}$ =rs_AB× s_CB=( $\begin{array}{l} 0 & r s β & - r c β \end{array}$ ), 则连杆BC在α =0时的运动螺旋为

$$_{CB} = (\begin{array}{l} \begin{array}{l} 1 & 0 & 0; \end{array} & \begin{array}{l} 0 & r s β & - r c β \end{array} \end{array}) (24)$

由式(24)可见在α =0时, 连杆BC绕x轴作单自由度连续旋转运动, 且转角为β .

当β =0时, Δ =cα , $_AB= $(- s α c α 0; 0)$ , $_B= $(001; r c αr s α 0)$ , 联立式(22)和(23)可解得s_CB=(cα sα 0); 线距 $s_{CB}^{0}$ =(0 0 -r), 则连杆BC的运动螺旋为

$$_{CB} = (\begin{array}{l} \begin{array}{l} c α & s α & 0; \end{array} & \begin{array}{l} 0 & 0 & - r \end{array} \end{array}) (25)$

且此时有s_CB· s_AB=0, 此时连杆BC的运动螺旋方向与两个连架杆的运动螺旋方向垂直.因此可见在β =0时, 连杆BC自由度性质为方向瞬时变化的平移运动, 瞬时平移方向与连杆AB垂直; 这时该空间四杆机构ABCD可以被视为一个瞬时运动方向变化的虚拟的平移运动副.

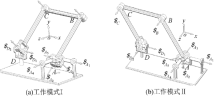
综上, 可重构空间四杆机构在一般位形下具有两种互斥的单自由度运动模式, 模型Ⅰ 为单轴转动模式, 模型Ⅱ 为虚拟的平移运动模式, 如图3所示.

	Figure Option View Download New Window
	图3 两种不同工作模式Fig.3 Two different working modes

3 运动仿真实验

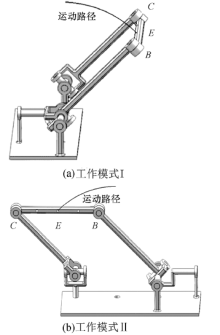
为验证上述理论分析的正确性, 这里使用SolidWorks的Motion功能对可重构空间四杆机构的运动进行仿真分析.首先选取球面五杆机构的构件3为旋转马达, 设置其作转速为7.5 r/min的匀速转动, 工作时间为1 s, 在Motion分析中选择跟踪路径功能, 得到连杆BC的中心点E点的运动路径如图4(a)所示.

	Figure Option View Download New Window
	图4 工作模式Ⅰ 和Ⅱ 的路径跟踪Fig.4 Path following of working modeⅠ and Ⅱ

其次选取球面五杆机构的构件1为旋转马达, 也设置其作转速为7.5 r/min的匀速转动, 工作时间为1 s, 在Motion分析中选择跟踪路径功能, 得到连杆BC的中心点E点的运动路径如图4(b)所示.

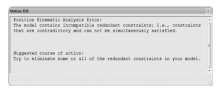
最后, 同时选取球面五杆机构的构件1和构件3为旋转马达, 其工作转速和时间设置同前, 并设置两个马达同时工作, 则仿真开始时弹出如图5所示的Motion分析对话框, 可见由于机构结构的设计决定机构约束的特点, 两个马达不能同时工作, 即可重构空间四杆机构的两种工作模式是互斥的.通过以上仿真实验验证上述理论分析是正确和有效的.

	Figure Option View Download New Window
	图5 Motion分析对话框Fig.5 Dialog box of Motion analysis

4 应用举例

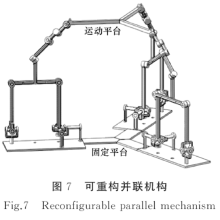
将可重构空间四杆机构与一个可实现2T2R(T代表移动, R代表转动)运动的串联支链^[7]相联, 则得到一个如图6所示的可重构混联支链, 用3条对称布置的混联支链连接运动平台和固定平台, 则可得到如图7所示的可重构并联机构.建立混联支链的局部坐标系O-xyz如图6所示, 坐标原点O位于直线AD和EF的交点, X轴与DA方向相同, Y轴垂直于机架.$_F、$_G、$_H和$_K组成2T2R运动串联支链, 其中$_F与直线AD相交于一点, 设$_F与直线AD的夹角为φ ; 其中$_G、$_H和$_K方向相同, 且不与$_F同向、相交和垂直, 设$_G是由$_F绕直线FG旋转角度γ 而得到的.图6中, 运动螺旋$_R表示可重构空间四杆机构可作绕X轴的旋转运动, 运动螺旋$_P表示可重构空间四杆机构可作XOY平面内的虚拟平移运动.当可重构空间四杆机构位于初始位置时, 混联支链的运动螺旋系为

$\{\begin{array}{l} $_{R} = (\begin{array}{l} 1 & 0 & 0; & 0 & 0 & 0 \end{array}) \\ $_{P} = (\begin{array}{l} 0 & 0 & 0; & 1 & 0 & 0 \end{array}) \\ $_{F} = (\begin{array}{l} c φ & s φ & 0; & 0 & 0 & f_{F_{0}} \end{array}) \\ $_{G} = (\begin{array}{l} c φ c γ & s φ c γ & - s γ; & d_{G_{0}} & e_{G_{0}} & f_{G_{0}} \end{array}) \\ $_{H} = (\begin{array}{l} c φ c γ & s φ c γ & - s γ; & d_{H_{0}} & e_{H_{0}} & f_{H_{0}} \end{array}) \\ $_{K} = (\begin{array}{l} c φ c γ & s φ c γ & - s γ; & d_{K_{0}} & e_{K_{0}} & f_{K_{0}} \end{array}) \end{array} (26)$

	Figure Option View Download New Window
	图6 可重构混联支链Fig.6 Reconfigurable hybrid limb

	Figure Option View Download New Window
	图7 可重构并联机构Fig.7 Reconfigurable parallel mechanism

式中:d_i、e_i和f_i(i=F₀, G₀, H₀, K₀)为与机构几何参数和运动参数有关的系数, 其不影响自由度的分析, 在此不必具体求解, 后续采用相同的方法描述.由式(26)可见, 混联支链的运动螺旋系的秩为6, 混联支链没有产生约束作用于图7所示可重构并联机构的运动平台, 因此该并联机构在初始位形的瞬时自由度为6.

当可重构空间四杆机构工作在工作模式Ⅰ 时, 即球面五杆机构的构件3为输入, 在局部坐标系O-xyz下, 可重构空间四杆机构绕X轴旋转β 角.此时混联支链的运动螺旋系为

$\{\begin{array}{l} $_{R} = (\begin{array}{l} 1 & 0 & 0; & 0 & 0 & 0 \end{array}) \\ $_{F} = (\begin{array}{l} c φ & s φ c β & s φ s β; & d_{F_{1}} & e_{F_{1}} & f_{F_{1}} \end{array}) \\ $_{G} = (\begin{array}{l} c φ c γ & s φ c γ c β + s γ s β & s φ c γ s β - s γ c β; & d_{G_{1}} & e_{G_{1}} & f_{G_{1}} \end{array}) \\ $_{H} = (\begin{array}{l} c φ c γ & s φ c γ c β + s γ s β & s φ c γ s β - s γ c β; & d_{H_{1}} & e_{H_{1}} & f_{H_{1}} \end{array}) \\ $_{K} = (\begin{array}{l} c φ c γ & s φ c γ c β + s γ s β & s φ c γ s β - s γ c β; & d_{K_{1}} & e_{K_{1}} & f_{K_{1}} \end{array}) \end{array} (27)$

可见, 在工作模式Ⅰ 时, 运动螺旋系的秩为5, 所以混联支链的自由度为5; 此时$_G、$_H和$_K可实现其所在平面内的2T1R运动, $_R和$_F可实现独立的2R运动, 因此混联支链将产生1个约束力矢作用于图7所示并联机构的运动平台.

当可重构空间四杆机构工作在工作模式Ⅱ 时, 即球面五杆机构的构件1为输入, 构件1转角为α , 在局部坐标系O-xyz下, 可重构空间四杆机构作虚拟平移运动.此时混联支链的运动螺旋系为

$\{\begin{array}{l} $_{P} = (\begin{array}{l} 0 & 0 & 0; & c α & s α & 0 \end{array}) \\ $_{F} = (\begin{array}{l} c φ & s φ & 0; & 0 & 0 & f_{F_{2}} \end{array}) \\ $_{G} = (\begin{array}{l} c φ c γ & s φ c γ & - s γ; & d_{G_{2}} & e_{G_{2}} & f_{G_{2}} \end{array}) \\ $_{H} = (\begin{array}{l} c φ c γ & s φ c γ & - s γ; & d_{H_{2}} & e_{H_{2}} & f_{H_{2}} \end{array}) \\ $_{K} = (\begin{array}{l} c φ c γ & s φ c γ & - s γ; & d_{K_{2}} & e_{K_{2}} & f_{K_{2}} \end{array}) \end{array} (28)$

由式(28)可得混联支链的约束螺旋为

$$_{P}^{r} = (\begin{array}{l} 0 & 0 & 0; & s φ & - c φ & 0 \end{array}) (29)$

可见在工作模式Ⅱ 时, 混联支链作用并联机构的运动平台一个约束力偶.

由图7可见, 3条混联支链为对称布置, 在空间上错开120° , 因此3条混联支链的约束螺旋是相互独立的, 即是线性无关的, 因此3条混联支链都位于初始位形时将无约束作用于运动平台, 图7中可重构并联机构的瞬时自由度为6; 当3条支链处于非初始位形时, 将有3个约束作用于可重构并联机构的运动平台, 机构的自由度为3.当3条混联支链均为工作模式Ⅰ 时, 运动平台受到3个约束力矢的作用, 运动平台可实现3R运动; 当3条混联支链均为工作模式Ⅱ 时, 运动平台受到3个约束力耦的作用, 运动平台可实现3T运动; 同理, 可重构混联机构因3条混联支链在不同运动模式间切换, 还可实现2R1T和2T1R运动.

5 结论

1)提出一种可重构空间四杆机构, 其具有1个转动和1个平动两种不同的工作模式.

2)利用该可重构空间四杆机构与一个可实现二移动和二转动运动的串联支链相连, 构成一种可重构混联支链, 该混联支链亦具有两种不同的工作模式.

3) 利用三条可重构混联支链连接并联机构的运动平台和固定平台, 可构造一种可重构并联机构, 该可重构并联机构具有四种不同的三自由度运动模式.

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	KONG X, GOSSELIN C M, RICHARD P. Type synthesis of parallel mechanisms with multiple operation modes[J]. Journal of Mechanical Design, 2007, 129: 595-601. [本文引用:1]
[2]	KONG X. Type synthesis of 3-DOF parallel manipulators with both a planar operation mode and a spatial translational operation mode[J]. Journal of Mechanisms and Robotics, 2013, 5: 041015. [本文引用:1]
[3]	李秦川, 陈巧红, 武传宇, 等. *变自由度4- ^xP^xR^xR^xR^yR_N并联机构[J]. 机械工程学报, 2009, 45(1): 83-87. LI Qinchuan, CHEN Qiaohong, WU Chuanyu, et al. 4- ^xP^xR^xR^xR^yR_N* parallel mechanism with variable mobility*[J]. Journal of Mechanical Engineering*, 2009, 45(1): 83-87. (in Chinese) [本文引用:1]
[4]	LI Q, HERVE J M. Parallel mechanism with bifurcation of schoenfiles motion[J]. IEEE Transaction on Robotics, 2009, 25(1): 158-164. [本文引用:1]
[5]	YE W, FANG Y F, ZHANG K T, et al. A new family of reconfigurable parallel mechanisms with diamond kinematotropic chain[J]. Mechanism and Machine Theory, 2014, 74: 1-9. [本文引用:1]
[6]	YE W, FANG Y, GUO S. Reconfigurable parallel mechanisms with three types of kinematotropic chains[C]// The 14th IFToMM World Congress, 2015: 25-30. [本文引用:1]
[7]	叶伟, 方跃法, 郭盛, 等. 基于运动限定机构的可重构并联机构设计[J]. 机械工程学报, 2015, 51(13): 137-143. YE Wei, FANG Yuefa, GUO Sheng, et al. Design of reconfigurable parallel mechanisms with discontinuously movable mechanism[J]. Journal of Mechanical Engineering, 2015, 51(13): 137-143. (in Chinese) [本文引用:2]
[8]	GAN D, DIAS J, SENEVIRATNE L. Unified kinematics and optimal design of a 3rRPS metamorphic parallel mechanism with a reconfigurable revolute joint[J]. Mechanism and Machine Theory, 2016, 96: 239-254. [本文引用:1]
[9]	GAN D, DAI J S, LIAO Q. Constraint analysis on mobility change of a novel metamorphic parallel mechanism[J]. Mechanism and Machine Theory, 2010, 45: 1864-1876. [本文引用:1]
[10]	ZHANG K, DAI J S, FANG Y. Geometric constraint and mobility variation of two 3SvPSv Metamorphic parallel mechanism[J]. Journal of Mechanical Design, 2013, 135: 1-8. [本文引用:1]
[11]	YE W, FANG Y, GUO S. Reconfigurable parallel mehanisms with planar five-bar metamorphic linkages[J]. Science China Technological Science, 2014, 57(1): 210-218. [本文引用:1]
[12]	KONG X, JIN Y. Type synthesis of 3-DOF multi-mode translational/spherical parallel mechanisms with lockable joints[J]. Mechanism and Machine Theory, 2016, 96: 323-333. [本文引用:2]
[13]	LEE C C, HERVE J M. A novel discontinuously movable six-revolute mechanism[C]// ASME/IFToMM International Conference on Reconfigurable Mechanisms and Robots, 2009: 58-62. [本文引用:3]
[14]	黄真, 刘婧芳, 李艳文. 论机构的自由度[M]. 北京: 科学出版社, 2011: 90-103. HUANG Zhen, LIU Jinfang, LI Yanwen. Mobility theory of mechanism[M]. Beijing: China Science Press, 2011: 90-103. (in Chinese) [本文引用:1]

2007

0.0

... 第1类可重构并联机构的重构过程发生在机构的约束奇异位置,如KONG等提出的多模式并联机构^[1,2] ...

2013

0.0

... 第1类可重构并联机构的重构过程发生在机构的约束奇异位置,如KONG等提出的多模式并联机构^[1,2] ...

2009

0.0

... 李秦川等提出的变自由度并联机构^[3]和可实现Schoenflies运动的并联机构^[4] ...

2009

0.0

... 李秦川等提出的变自由度并联机构^[3]和可实现Schoenflies运动的并联机构^[4] ...

2014

0.0

... YE和FANG等将约束奇异由并联机构支链间转移至支链内部,即通过闭链的约束奇异实现混联支链的重构,提出了一类可重构并联机构构型综合的新方法,综合出一系列含约束奇异特性单环闭链的可重构并联机构^[5,6,7] ...

2015

0.0

2015

0.0

叶伟, 方跃法, 郭盛, 等. 基于运动限定机构的可重构并联机构设计[J]. 机械工程学报, 2015, 51(13): 137-143.

Wei

, FANG

Yuefa

, GUO

Sheng

, et al. Design of reconfigurable parallel mechanisms with discontinuously movable mechanism[J]. Journal of Mechanical Engineering, 2015, 51(13): 137-143. (in Chinese)

分析在特殊杆长条件下一种运动限定机构的运动特性。在不同的构型下,运动限定机构可以分别执行一个转动加一个平移运动、一个平移运动、一个转动运动。将运动限定机构与具有两个转动和两个移动运动的串联支链相结合,设计出一类具有可重构特性的混联支链。基于李群理论,得到了混联支链在不同构型下运动的群论表达式。利用三条同样的混联支链连接动平台和定平台,得到了一类新型可重构并联机构。当所有混联支链中的运动限定机构处于奇异位置时,可重构并联机构具有瞬时的6自由度。通过控制运动限定机构运行至不同的构型,可重构并联机构能切换至不同的自由度模式,可以执行四种不同特性的3自由度运动。

... 4 应用举例将可重构空间四杆机构与一个可实现2T2R(T代表移动,R代表转动)运动的串联支链^[7]相联,则得到一个如图6所示的可重构混联支链,用3条对称布置的混联支链连接运动平台和固定平台,则可得到如图7所示的可重构并联机构 ...

2016

0.0

... S代表球副)变胞并联机构^[8] ...

2010

0.0

... GAN等提出一种具有两种不同子构态的rT变胞运动副(可重构虎克铰链),该变胞运动副可在虎克铰和转动副之间切换,利用该变胞运动副构型了一类变胞并联机构,并利用螺旋理论对其自由度进行了分析^[9] ...

2013

0.0

... ZHANG等提出一种具有3种不同子构态的vA运动副(变轴线关节),该变胞运动副可实现球副、虎克铰和转动副3种不同子构态的切换,利用螺旋理论分析了vA运动副构态变化机理,并利用该变胞运动副构型了一类3S_vPS_v(S_v为可重构球副)变胞并联机构^[10] ...

2014

0.0

... YE和FANG利用闭链机构的支链奇异特性,将具有3种不同子构态的平面五杆机构与串联支链混联构造可重构混联支链,应用螺旋理论构型出可实现10种不同运动模式的可重构并联机构^[11] ...

2016

0.0

... 由上述分析可见,可重构并联机构的重构位置一般发生在机构的约束奇异位置或者机构的支链奇异位置,为避免机构在重构时经过上述奇异位置,KONG等利用关节锁死的方法,综合了一种三自由度多操作模式并联机构^[12] ...

... 根据上述分析可以发现,现有的可重构并联机构仍然比较少,可重构并联机构的设计往往依赖于设计者的灵感,设计者巧妙地将变胞运动副、可锁死关节、可重构运动平台^[12]、运动分叉单环闭链^[13]及平面变胞机构等引入并联机构设计进而实现并联机构的可重构 ...

2009

0.0

... 空间四杆机构可以视为一种广义并联机构,不同于文献[13]所提出的可重构单环闭链机构,将二自由度球面五杆机构引入到可重构并联机构设计,用其替代了文献[13]中的1个虎克铰链,利用球面二自由度五杆机构实现机构整体的二自由度并联驱动输入,得到一种可重构空间四杆机构,利用螺旋理论对其自由度特性进行了分析 ...

2011

0.0

... 除去公共约束剩余6个反螺旋组成一个3系螺旋,所以初始位形下机构的并联冗余约束数为v=6-3=3,由修正的G-K公式^[14]可得在初始位形下机构的自由度为 ...