中等压缩性土地基工后沉降预测三参数幂函数模型

引用本文

罗强, 程明, 王腾飞, 朱江江. 中等压缩性土地基工后沉降预测三参数幂函数模型[J]. 北京交通大学学报, 2020,44(3): 93-100.
LUO Qiang, CHENG Ming, WANG Tengfei, ZHU Jiangjiang. Three-parameter power function model for prediction of post-construction settlement of medium compressive soil foundation[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2020,44(3): 93-100.
Doi:10.11860/j.issn.1673-0291.20190078 复制到剪切板

Permissions

北京交通大学学报编辑部所有

中等压缩性土地基工后沉降预测三参数幂函数模型

罗强^1a,^1b, 程明^1a,^1b, 王腾飞^1a,^1b, 朱江江^1a,²

1.西南交通大学 a.土木工程学院,b.高速铁路线路工程教育部重点实验室,成都 610031

2.中铁第四勘察设计院集团有限公司,武汉 430063

第一作者:罗强(1963— ),男,四川宜宾人,教授,博士,博士生导师.研究方向为铁路路基工程.email:lqrock@home.swjtu.edu.cn.

收稿日期: 2019-07-16

基金: 国家自然科学基金(51878560)

摘要

基于最终沉降量、沉降半衰期及半衰期沉降速率表征的沉降-时间关系曲线的特征方程,分析了传统两参数双曲线和指数曲线模型存在的缺陷,构建了一个三参数的幂函数型沉降预测模型;结合蒙华重载铁路某段粉质黏土地基沉降观测数据,以均方差、关联度和偏离度为检验指标,开展了中等压缩性土地基工后沉降预测模型的准确性评价.研究表明:三参数幂函数模型较传统两参数模型能适应更多样化的沉降-时间曲线形态,在表征沉降预测有效性的检验指标方面表现更佳;以满足规范要求的工后256 d观测数据预测地基528 d沉降,三参数幂函数模型的平均偏离度仅为5.99%,而传统两参数模型分别14.38%和22.46%.本研究提供了一种新的地基工后沉降预测方法,具有一定的工程应用价值.

关键词: 工后沉降预测; 三参数幂函数模型; 检验指标; 中等压缩性土; 蒙华重载铁路

中图分类号:U213.14 文献标志码:A 文章编号:1673-0291(2020)03-0093-08

Three-parameter power function model for prediction of post-construction settlement of medium compressive soil foundation

LUO Qiang^1a,^1b, CHENG Ming^1a,^1b, WANG Tengfei^1a,^1b, ZHU Jiangjiang^1a,²

1a. School of Civil Engineering, 1b. MOE Key Laboratory of High-speed Railway Engineering, Southwest Jiaotong University, Chengdu 610031, China

2. China Railway Siyuan Survey and Design Group Co., Ltd., Wuhan 430063, China

Fund:National Natural Science Foundation of China (51878560)

Abstract

The characteristic equation representing the settlement-time relationship was built based on final settlement valve, half-life time settlement and half-life time settlement rate. The mathematical deficiencies of the traditional two-parameter hyperbolic model and exponential model are revealed, and a three-parameter power function model for post-construction settlement prediction is established. Using the observation settlement data of silty clay foundation in a section of Menghua heavy-haul railway, mean square error, correlation and deviation are employed as the detection indicators to evaluate the accuracy of the predicting model for post-construction settlement of medium compressive soil foundation.According to the results, compared with the traditional models, the three-parameter power function model can adapt to more settlement-time curve shapes and show more ideal test indicators. The settlement data within 256 days after construction is used to predict the settlement value on 528 days,which meets the requirements of the specification for observation time. Average deviation of the three-parameter model reaches only 5.99%, while that of the traditional models are 14.38% and 22.46%, respectively.The research provides a new predict method for post-construction settlement of soil foundation,which bears engineering application value.

Keyword: prediction to post-construction settlement; three-parameter power function model; detection indicators; medium compressive soil; Menghua heavy-haul railway

文章图片

路堤荷载作用下的路基工后沉降主要由地基压缩变形引起.因此, 准确有效地分析和预测地基工后沉降量, 成为路基工程中的一个重要课题.高压缩性的软土和松软土地基, 因承载力低、沉降量大, 一直是路基沉降控制关注的热点, 已有较多的工程经验和研究成果.对于重载铁路路堤作用下的中等压缩性土地基, 无论是在地基的沉降变形规律, 还是合理的加固处理措施等方面都缺乏系统的研究.为此, 开展现场地基沉降观测试验以及沉降预测分析对于确保铁路安全运营具有重要意义.

国内外学者针对地基沉降评价方法已做了较多的相关研究.弹性理论法^[1]是将土体视为弹性体, 只在某些符合弹性理论基本假设的理想条件下可以采用, 对于一般地基, 由于土的压缩特性随处变化等因素, 使得此类方法较少被采用; 现场试验法^[2]在建立现场试验结果与土性质间相关关系的过程中无法计及土层的应力历史等因素, 故其可靠性依赖工程经验; 数值计算法以有限元法^[3]为主, 所涉及的计算参数较多, 且成果可靠性取决于所用模型的代表性与输入指标的正确性; 分层总和法^[4]是应用最多的方法, 其要求土体的分层厚度不能过大, 且土分层压缩模量不变, 但基于钻探资料的土层划分常常比较粗糙, 并且主要通过室内压缩试验确定的压缩模量, 受扰动、试样尺寸等因素影响, 与现场实际往往不符, 导致地基预测沉降量与实际沉降量会有出入.在目前的各类计算方法中, 由于在计算模型、荷载条件等方面作了简化, 所用的土性计算指标易受试验中自然和人为因素影响, 沉降计算结果较实际沉降往往有不同程度的差异.因此, 研究者结合沉降监测数据提出了一些曲线拟合方法:陈善雄等^[5]针对武广高铁沉降量级小、实测数据相对波动大的特点, 将三点法引入双曲线模型中预测路基沉降.杨涛等^[6]基于分级填筑路堤的各级沉降发展形态是近似双曲线变化趋势的规律, 提出一种考虑了地基土变形非线性和固结性质随荷载变化的沉降预测模型.赵亚红等^[7]根据泊松、指数曲线模型各个时刻预测精度不同来赋予不同权值, 建立了一种基于IOWHA算子的泊松-指数曲线加权组合预测模型.以上曲线拟合方法都是在认为路基沉降的整体或部分规律接近双曲线或指数曲线变化趋势的基础上, 直接或间接采用双曲线或指数曲线模型来对路基沉降展开分析预测, 但是否可以采用更优的模型来进行沉降预测还有待研究.

鉴于此, 本文建立了地基工后沉降-时间曲线的数学特征方程, 通过特征方程发现, 传统两参数双曲线和指数曲线模型在最终沉降量、沉降半衰期一定时, 半衰期沉降速率也随即为定值, 使得模型的适应性差; 三参数幂函数模型克服了两种传统模型的不足, 其曲线形态丰富, 不仅拟合度更优, 预测准确性也更高.结合蒙华重载铁路新余段的地基工后沉降实测数据, 提出了均方差、关联度和偏离度为预测模型有效性的检验指标, 综合对比结果验证了三参数幂函数模型的可行性.

1 传统两参数预测模型

1.1 双曲线模型

双曲线模型常采用的表达式为^[8]

$S_{1} (t) = \frac{t}{α + βt}$ (1)

式中:S₁(t)为任意时刻双曲线模型预测的工后沉降量; t为任意时刻; α 、β 为待定参数.

由式(1)知, 地基工后的最终沉降量 $S_{\infty}$ =1/β .对式(1)求一阶导数, 得地基工后沉降速率V_t=α /(α +β t)²; 当t=0时, 初始沉降速率V₀=1/α .

1.2 指数曲线模型

指数曲线模型常采用的表达式为^[9]

$S_{2} (t) = A (1 - e^{- Bt})$ (2)

式中:S₂(t)为任意时刻指数曲线模型预测的工后沉降量; A、B为待定参数.

由式(2)可得, $S_{\infty}$ =A、V_t=ABe^-^Bt、V₀=AB.

两参数的双曲线和指数曲线模型表达式简单, 且参数均具有较明确的物理意义, 因而得到了较为广泛的应用.然而, 两参数双曲线模型只是在模型曲线形状与实测沉降变形曲线形状相似的基础上提出, 预测结果通常偏大^[10]; 两参数指数曲线模型是基于一维固结理论建立的模型, 只考虑了主固结沉降, 而忽略了次固结沉降的影响, 所以推算结果通常偏小^[11].

1.3 传统模型沉降时程曲线特征

大量试验数据表明, 两个传统模型在拟合地基工后沉降时, 既有拟合较为理想^[12]的情况, 也有拟合较差^[13]的情况.导致这种情形的根本原因在于两个模型的局限性.

两参数的双曲线模型和指数曲线模型的特征方程分别为

$\{\begin{array}{l} S_{\infty} = 1 / β \\ t_{[1 / 2]} = α / β \\ V_{[1 / 2]} = 1 / (4 α) \end{array}$ (3)

$\{\begin{array}{l} S_{\infty} = A \\ t_{[1 / 2]} = \ln 2 / B \\ V_{[1 / 2]} = (AB) / 2 \end{array}$ (4)

式中:t_[1_/_2]为沉降半衰期, 是指工后沉降量达到最终工后沉降量的50%时所对应的时间^[14]; V_[1_/_2]为半衰期沉降速率, 是指工后沉降量达到最终工后沉降量的50%时所对应的沉降速率.当最终沉降量 $S_{\infty}$ 和沉降半衰期t_[1_/_2]一定时, 半衰期沉降速率V_[1_/_2]的大小可以影响沉降收敛的快慢.最终沉降量 $S_{\infty}$ 、沉降半衰期t_[1_/_2]和半衰期沉降速率V_[1_/_2]的表达式共同组成了工后沉降-时间曲线的特征方程, 能较好反映沉降时程曲线的全过程.

当最终沉降量和沉降半衰期确定后, 半衰期沉降速率不可调, 这反映了传统两参数双曲线和指数曲线模型的数学理论缺陷.实际上, 即使最终沉降量和沉降半衰期确定, 半衰期沉降速率还可能与路基填筑速度、土体自身性质等因素有关.较为理想的工后沉降预测模型应能保证这三个量之间相互独立.

2 地基沉降三参数预测模型

2.1 幂函数曲线模型

大量实测沉降的资料表明, 地基沉降随时间的发展规律各不相同, 沉降-时间曲线形式多样.对取自现场的地基土进行固结试验, 发现“ L-模型” ^[15]曲线与固结曲线的拟合度非常高, 基于地基沉降是地基土压缩变形的宏观体现这一基本认识, 且考虑地基工后沉降变形曲线过原点, 故对“ L-模型” 进行简化, 提出了一种适用于地基工后沉降预测的三参数幂函数模型, 模型表达式为

$S_{3} (t) = m_{0} [1 - \frac{1}{1 + (t / m_{2})^{m_{1}}}]$ (5)

式中:S₃(t)为任意时刻三参数幂函数模型预测的工后沉降量; m₀> 0, m₁> 0, m₂> 0为待定参数.

由式(5)可知, 三参数幂函数模型具有如下特点:

1)过原点.

当t=0时, S₃(t)=0, 符合工后沉降的特点.

2)单调性.

V_t=m₀m₁m₂ $^{- m_{1}} t^{m_{1} - 1}$ / $[(t / m_{2})^{m_{1}} {+ 1]}^{2}$ > 0, 随着t值的增大, 此模型单调递增, 可以体现沉降的一般规律.

3)有界性.

t→ ∞时, S₃(t)→ m₀, 表明当时间趋于无穷时, 沉降趋于稳定.

4)良好适应性.

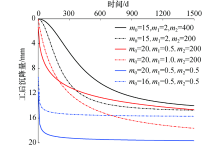
模型参数值变化, 对应沉降曲线见图1, 表明模型能描述不同的曲线形态.

	Figure Option View Download New Window
	图1 不同参数值对应的沉降曲线Fig.1 Settlement curves under different parameters

基于以上特点, 三参数幂函数模型预测地基工后沉降具有广泛的适应性.

2.2 三参数幂函数模型沉降时程曲线特征

根据式(5)可知, 三参数幂函数模型的特征方程为

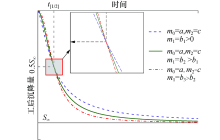
$\{\begin{array}{l} S_{\infty} = m_{0} \\ t_{[1 / 2]} = m_{2} \\ V_{[1 / 2]} = m_{0} m_{1} / (4 m_{2}) \end{array}$ (6)

在最终沉降量和沉降半衰期一定时, m₀、m₂是确定的, 但m₁仍然可以相对自由取值, 即半衰期沉降速率V_[1_/_2]可以相对自由.m₁的值越大, V_[1_/_2]的值就越大, 沉降收敛就越快, 半衰期沉降速率与曲线收敛快慢关系见图2.图2中, 当m₀、m₂分别取定值a、c时, m₁取定值b₁、b₂或b₃将会影响收敛快慢.因此, 从这个角度来说, 三参数幂函数模型比传统两参数双曲线和指数曲线模型能更好地拟合多种变化规律的实测数据, 对于实际情况具有更强适应性.

	Figure Option View Download New Window
	图2 半衰期沉降速率与曲线收敛快慢关系Fig.2 Relationship between the half-life time settlement rate and the curve convergence speed

3 案例分析

3.1 工程概况

蒙华重载铁路起于内蒙古浩勒报吉, 止于江西吉安, 是国内目前最长的运煤专线.选取江西新余境内6个断面的地基工后沉降实测数据进行分析, 观测点位于测试路基横断面中心线的地基面.沉降观测采用单点沉降计进行, 单点沉降计上端的沉降板埋设于地基面, 下端与加长杆相连, 加长杆的另一端与底层锚头焊接, 并将底层锚头锚固到基岩(相对不动点).地基沉降变形时, 沉降板随地基面一起下沉, 并通过传感器输出沉降变形值.

试验段地基土主要是粉质黏土、软质千枚岩, 标准压缩系数a₁_~₂在0.1~ 0.4 MPa^-1范围内, 属于中等压缩性土, 见表1.

表1 断面概况 Tab.1 Overview of section

断面	地基土层成分 (从地基面往下)	单点沉降计埋深/m	路基填高/m
DK1806 +775	$Q_{4}^{el + dl}$ 粉质黏土(厚0.61 m)及全风化(厚8.43 m)、强风化(厚7.58 m)和弱风化软质千枚岩	10.0	11.11
DK1806 +800	$Q_{4}^{el + dl}$ 粉质黏土(厚1.00 m)及全风化(厚7.80 m)、强风化(厚7.83 m)和弱风化软质千枚岩	10.0	11.12
DK1806 +900	$Q_{4}^{dl + pl}$ 淤泥质粉质黏土(厚1.40 m)、 $Q_{4}^{dl + pl}$ 粉质黏土(厚2.00 m)及全风化(厚7.60 m)和强风化软质千枚岩	12.0	14.13
DK1806 +925	$Q_{4}^{dl + pl}$ 淤泥质粉质黏土(厚1.32 m)、 $Q_{4}^{dl + pl}$ 粉质黏土(厚2.08 m)及全风化(厚7.53 m)和强风化软质千枚岩	11.0	14.28
DK1807 +150	$Q_{4}^{dl + pl}$ 粉质黏土(厚2.09 m)以及全风化(厚10.08 m)和强风化软质千枚岩	13.0	13.27
DK1807 +250	$Q_{4}^{dl + pl}$ 粉质黏土(厚1.00 m)、细角砾土(厚2.00 m)及全风化(厚4.08 m)和强风化软质千枚岩	8.0	12.70

表1 断面概况 Tab.1 Overview of section

DK1806+775和DK1806+800断面的基床以下路堤采用掺配比为3.5%的水泥改良土填筑(掺配比为干掺料质量与干土质量之比); 其余4个断面均采用全风化软质岩直接填筑.6个断面的路基高度均大于8.0 m, 为提高路基稳定性, 在路肩以下8.0 m处设置3.0 m宽平台, 平台以上边坡坡率为1∶ 1.5, 平台以下坡率采用1∶ 1.75.全风化软质岩填料最主要的矿物成分为石英和富铁白云母, 其质量百分比分别为69.5%和17.3%, 所含黏土矿物为高岭石和绿泥石, 含量分别为2.1%和1.1%.

路基于2017年9月11日填筑完成, 并以路基填筑完成时刻为时间起点, 到路基填筑完成后528 d内的地基工后沉降实测值见表2.

表2 工后沉降实测值 Tab.2 Actual measured values of post-construction settlement

3.2 不同预测模型拟合效果对比

结合最小均方差和最大关联度两种不同评价标准的辨识方法, 对不同模型的拟合结果进行综合对比分析.

3.2.1 最小均方差

将实测沉降值与预测沉降值的差值平方求和后, 除以该组数据样本量n, 得该组数据的均方差为

$σ_{k} = \frac{1}{n} \sum [S_{t} - S_{k} {(t)]}^{2}$ (7)

式中:σ _k为数据均方差; S_t为实测沉降值; S_k(t)为预测沉降值; k=1, 2, 3, 分别表示两参数双曲线模型、两参数指数曲线模型、三参数幂函数模型.

由式(7)可知, σ _k值最小的模型拟合曲线最优.

3.2.2 最大关联度

关联度可以反映不同时刻下预测值与实测值的联系紧密程度, 关联度计算式为

$ω_{k} (t) = \frac{\min_{k} \min_{t} |S_{t} - S_{k} (t)| + λ \max_{k} \max_{t} |S_{t} - S_{k} (t)|}{|S_{t} - S_{k} (t)| + λ \max_{k} \max_{t} |S_{t} - S_{k} (t)|}$ (8)

$η_{k} = \frac{1}{n} \sum ω_{k} (t)$ (9)

式中:ω _k(t)为关联系数, 是指模型k得到t时刻预测值与t时刻实测值的相对差值; η _k为关联度; λ 为分辨系数, 取λ =0.5.

由式(9)可知, η _k值最大的为最优曲线.

3.2.3 拟合效果对比分析

取路基填筑完成后528 d内的沉降观测数据建立模型, 三个模型的拟合结果见表3.根据评价标准, 当σ _k趋于0且η _k趋于1时模型最优.因此可知, 6个断面无论是关联度指标还是均方差指标均判断三参数幂函数模型拟合的更好.

表3 不同预测模型的拟合结果 Tab.3 Fitting results of different prediction models

从均方差和关联度的波动范围看, 三参数幂函数模型的均方差σ _k在0.010~0.272范围内波动, 平均值为0.076; 两参数双曲线模型的σ _k在0.040 ~ 0.323范围内, 平均值为0.205; 两参数指数曲线模型的相应值分别为0.064 ~ 0.653及0.342.三参数幂函数模型的关联度η _k在0.737~0.857范围内波动, 平均值为0.813; 两参数双曲线模型的η _k在0.627 ~ 0.816范围内, 平均值为0.701; 两参数指数曲线模型的相应值分别为0.510 ~ 0.804及0.646.因此, 从三参数幂函数模型在实际工程中的应用来看, 其对实测沉降的拟合效果要优于两种传统模型.

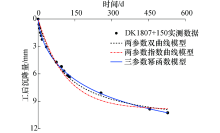
针对DK1807+150断面, 实测的地基工后沉降数据以及三种模型分别对实测数据进行拟合的曲线见图3.由图3可见, 三参数幂函数模型对实测沉降的拟合更好一些.

	Figure Option View Download New Window
	图3 实测沉降值与不同模型拟合曲线Fig.3 Measured values and different fitting curves

3.3 工后沉降预测准确性评价

为评价模型预测的准确性, 提出了描述预测值S_k(t)与实测值S_t偏离程度的量化指标即偏离度, 其表达式为

$M_{k} = \frac{S_{k} (t) - S_{t}}{S_{t}} \times 100 %$ (10)

式中:M_k为偏离度.

由式(10)可见, 偏离度的绝对值越小, 表明预测结果越接近于实测值, 偏离度是反映预测结果有效性的一个指标.另外, 偏离度也可判断预测值偏于安全或危险, 若偏离度为负值, 表明预测结果比实测值小, 偏于危险; 若偏离度为正值, 在工程上是安全的.

分别用路基填筑完成后256、455 d内的实测数据建立3种模型, 并计算对应的第528 d沉降预测值.偏离度对比结果见图4.

	Figure Option View Download New Window
	图4 不同预测模型偏离度对比Fig.4 Deviation comparison of different prediction models

定义平均偏离度为模型所拟合断面的偏离度绝对值的平均值.由平均偏离度的定义可知, 其值越小, 对应模型的预测准确性越高, 不同预测模型的平均偏离度见表4.

表4 不同预测模型的平均偏离度 Tab.4 Average deviation of different prediction models %

由图5可见, 采用路基填筑完成后256 d内的实测数据进行预测时, 两参数双曲线模型的偏离度M_k在-18.25%~-8.65%范围内波动, 两参数指数曲线模型的M_k在-25.67%~-16.81%范围内, 三参数幂函数模型的相应值为-18.10%~-0.62%, 3个模型的偏离度均为负值, 但是表4反映出三参数幂函数模型的平均偏离度5.99%远小于双曲线模型的14.38%和指数曲线模型的22.46%, 并且除了DK1806+775断面, 其余断面三参数幂函数模型的偏离度绝对值都在10%以内, 其中以在5%以内居多.

实测数据增加到455 d时, 两参数双曲线模型的偏离度M_k在-7.15%~-3.40%范围内波动, 两参数指数曲线模型的M_k在-9.75%~3.37%范围内, 三参数幂函数模型的相应值为-2.27%~0.59%, 3个模型的偏离度绝对值均减小, 反映出随着监测时间的增加, 3个模型的预测准确性均有所提高, 但三参数幂函数模型的偏离度绝对值全部在5%以内, 平均偏离度1.23%也小于双曲线模型的5.30%和指数曲线模型的7.56%.

因此, 同样的监测时间下, 三参数幂函数模型要比其他两种传统模型的预测准确性更高, 在工程应用中相对更安全.

3.4 地基的最终工后沉降预测

由前述分析可知, 三参数幂函数模型优于两种传统模型且预测准确性随着监测时间的增加而提高.因此, 除DK1806+900断面采用路基填筑完成后455 d内实测数据建立三参数幂函数模型预测最终工后沉降量, 其余断面均用528 d内实测数据建模.将施工期沉降和由表3可得的最终工后沉降预测值列于表5.

表5 施工期沉降及预测的最终工后沉降量 Tab.5 Settlement values during construction and predicted final post-construction settlement

由表5可知, 工后沉降在17.21~ 38.18 mm范围内, 远小于我国TB 10001—2016《铁路路基设计规范》要求的重载铁路路基工后沉降控制限值200 mm^[16], 表明由粉质黏土和全风化软质岩组成的中等压缩性土地基在一般路堤荷载作用下的工后沉降能满足重载铁路路基沉降控制的要求.工后沉降与路基填土高度的比值为1.30~3.43; 施工期沉降与路基填土高度之比为4.56~11.61.工后沉降占总沉降的比例在15.07%~32.03%范围内, 不超过50%, 表明沉降主要在施工期完成.

4 结论

通过分析地基沉降时程曲线的特征方程, 指出了传统两参数双曲线和指数曲线模型存在适应性差的数学缺陷, 给出了适用于路堤作用下地基工后沉降预测的三参数幂函数模型, 并结合蒙华重载铁路路基沉降观测数据, 对模型的拟合效果和预测准确性进行评价, 得到以下结论:

1)三参数幂函数模型能较好地描述路基的沉降-时间关系变化趋势, 在反映沉降预测准确性的均方差、关联度、偏离度等方面较传统两参数模型更优, 其实质是表征沉降-时间关系曲线的最终沉降量、沉降半衰期和半衰期沉降速率3个特征量相互独立.

2)由路基填筑完成后的256 d内观测数据, 进行第528 d地基沉降的预测准确性分析可知, 三参数幂函数模型的偏离度在-18.10%~-0.62%范围内, 平均偏离度仅为5.99%, 而传统两参数模型的偏离度在-25.67%~-8.65%范围内, 平均偏离度分别增大至14.38%和22.46%; 且预测的准确性随监测时间的增加而提高.

3)基于三参数幂函数模型预测的地基最终工后沉降量为17.21~38.18 mm, 约占总沉降量的15.07%~32.03%, 与11.11~14.28 m路基填高的比值为1.30~3.43.研究结果表明, 由粉质黏土和全风化软质岩组成的中等压缩性土地基在一般路堤荷载作用下, 工后沉降能满足重载铁路路基沉降控制的要求.

参考文献

文献列表

[1]	林旭武. 组合桩复合地基性状及沉降计算研究[D]. 杭州: 浙江大学, 2005. LIN Xuwu. Research on behavior and settlement calculation of combined composite foundation[D]. Hangzhou: Zhejiang University, 2005. (in Chinese) [本文引用:1]
[2]	李广信. 高等土力学[M]. 北京: 清华大学出版社, 2004: 252-267. LI Guangxin. Advanced soil mechanics[M]. Beijing: Tsinghua University Press, 2004: 252-267. (in Chinese) [本文引用:1]
[3]	崔凯, 杨文恒. 软土路基沉降的联合法预测研究[J]. 西南交通大学学报, 2017, 52(5): 926-934. CUI Kai, YANG Wenheng. Prediction soft soil settling using a combination method[J]. Journal of Southwest Jiaotong University, 2017, 52(5): 926-934. (in Chinese) [本文引用:1]
[4]	童立元, 涂启柱, 刘松玉, 等. 基于孔压静力触探测试的改进分层总和法在软基沉降预测中的应用研究[J]. 岩土力学, 2011, 32(增2): 679-682. TONG Liyuan, TU Qizhu, LIU Songyu, et al. Settlement prediction of soft ground by modified layer wise summation method based on piezocone tests[J]. Rock and Soil Mechanics, 2011, 32(S2): 679-682. (in Chinese) [本文引用:1]
[5]	陈善雄, 王星运, 许锡昌, 等. 铁路客运专线路基沉降预测的新方法[J]. 岩土力学, 2010, 31(2): 478-482. CHEN Shanxiong, WANG Xingyun, XU Xichang, et al. New method for forecasting subgrade settlement of railway passenger dedicated line[J]. Rock and Soil Mechanics, 2010, 31(2): 478-482. (in Chinese) [本文引用:1]
[6]	杨涛, 李国维, 杨伟清. 基于双曲线法的分级填筑路堤沉降预测[J]. 岩土力学, 2004, 25(10): 1551-1554. YANG Tao, LI Guowei, YANG Weiqing. Settlement prediction of stage constructed embankment on soft ground based on the hyperbolic method[J]. Rock and Soil Mechanics, 2004, 25(10): 1551-1554. (in Chinese) [本文引用:1]
[7]	赵亚红, 王金星, 张丽华, 等. 基于IOWHA算子的路基沉降加权组合预测方法研究[J]. 铁道科学与工程学报, 2018, 15(10): 2529-2534. ZHAO Yahong, WANG Jinxing, ZHANG Lihua, et al. Study on weighted combination model based on IOWHA operator in prediction of subgrade settlement[J]. Journal of Railway Science and Engineering, 2018, 15(10): 2529-2534. (in Chinese) [本文引用:1]
[8]	金亮星, 李小刚. 泊松曲线法在填海造地道路软基沉降预测中的应用[J]. 铁道科学与工程学报, 2013, 10(5): 52-56. JIN Liangxing, LI Xiaogang. Application of Poisson curve method in the prediction of road soft foundation settlement for land reclamation[J]. Journal of Railway Science and Engineering, 2013, 10(5): 52-56. (in Chinese) [本文引用:1]
[9]	陈善雄, 王星运, 许锡昌, 等. 路基沉降预测的三点修正指数曲线法[J]. 岩土力学, 2011, 32(11): 3355-3360. CHEN Shanxiong, WANG Xingyun, XU Xichang, et al. Three-point modified exponential curve method for predicting subgrade settlements[J]. Rock and Soil Mechanics, 2011, 32(11): 3355-3360. (in Chinese) [本文引用:1]
[10]	胡中雄. 土力学与环境土工学[M]. 上海: 同济大学出版社, 1997: 175-179. HU Zhongxiong. Soil mechanics and environmental geotechnical engineering[M]. Shanghai: Tongji University Press, 1997: 175-179. (in Chinese) [本文引用:1]
[11]	吕秀杰. 软土地基工后沉降预测模型的研究[J]. 岩土力学, 2009, 30(7): 2091-2095. LYU Xiujie. Research on estimation modle of post construction settlement for soft ground[J]. Rock and SoilMechanics, 2009, 30(7): 2091-2095. (in Chinese) [本文引用:1]
[12]	王丽琴, 靳宝成, 杨有海, 等. 黄土路基工后沉降预测模型对比研究[J]. 铁道学报, 2008, 30(1): 43-47. WANG Liqin, JIN Baocheng, YANG Youhai, et al. Contrast study on prediction models of settlement of loess-fill subgrade after construction[J]. Journal of the China Railway Society, 2008, 30(1): 43-47. (in Chinese) [本文引用:1]
[13]	冯怀平, 耿会岭, 马德良, 等. 高速铁路非饱和路基沉降特性及预测研究[J]. 铁道学报, 2017, 39(11): 138-143. FENG Huaiping, GENG Huiling, MA Deliang, et al. Study on settlement property and prediction for high-speed railway subgrade[J]. Journal of the China Railway Society, 2017, 39(11): 138-143. (in Chinese) [本文引用:1]
[14]	王伟, 孙斌祥, 卢廷浩. 公路路堤软土地基工后沉降的三参数预估模型[J]. 中国公路学报, 2008, 21(2): 12-17. WANG Wei, SUN Binxiang, LU Tinghao. 3-parameter prediction model of post-construction settlement for soft soil foundation under highway embankment[J]. China Journal of Highway and Transport, 2008, 21(2): 12-17. (in Chinese) [本文引用:1]
[15]	朱志铎, 周礼红. 软土路基全过程沉降预测的Logistic模型应用研究[J]. 岩土工程学报, 2009, 31(6): 965-969. ZHU Zhiduo, ZHOU Lihong. Application of Logistic model in settlement prediction during complete process of embankment construction[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(6): 965-969. (in Chinese) [本文引用:1]
[16]	国家铁路局. 铁路路基设计规范: TB 10001—2016[S]. 北京: 中国铁道出版社, 2017: 18-24. National Railway Administration of the PRC. Code for design of railway earth structure: TB 10001—2016[S]. Beijing: China Railway Publishing House, 2017: 18-24. (in Chinese) [本文引用:1]

2005

0.0

... 弹性理论法^[1]是将土体视为弹性体,只在某些符合弹性理论基本假设的理想条件下可以采用,对于一般地基,由于土的压缩特性随处变化等因素,使得此类方法较少被采用 ...

2004

0.0

... 现场试验法^[2]在建立现场试验结果与土性质间相关关系的过程中无法计及土层的应力历史等因素,故其可靠性依赖工程经验 ...

2017

0.0

... 数值计算法以有限元法^[3]为主,所涉及的计算参数较多,且成果可靠性取决于所用模型的代表性与输入指标的正确性 ...

2011

0.0

... 分层总和法^[4]是应用最多的方法,其要求土体的分层厚度不能过大,且土分层压缩模量不变,但基于钻探资料的土层划分常常比较粗糙,并且主要通过室内压缩试验确定的压缩模量,受扰动、试样尺寸等因素影响,与现场实际往往不符,导致地基预测沉降量与实际沉降量会有出入 ...

2010

0.0

... 因此,研究者结合沉降监测数据提出了一些曲线拟合方法:陈善雄等^[5]针对武广高铁沉降量级小、实测数据相对波动大的特点,将三点法引入双曲线模型中预测路基沉降 ...

2004

0.0

... 杨涛等^[6]基于分级填筑路堤的各级沉降发展形态是近似双曲线变化趋势的规律,提出一种考虑了地基土变形非线性和固结性质随荷载变化的沉降预测模型 ...

2018

0.0

... 赵亚红等^[7]根据泊松、指数曲线模型各个时刻预测精度不同来赋予不同权值,建立了一种基于IOWHA算子的泊松-指数曲线加权组合预测模型 ...

2013

0.0

... 1 双曲线模型双曲线模型常采用的表达式为^[8] ...

2011

0.0

... 2 指数曲线模型指数曲线模型常采用的表达式为^[9] ...

1997

0.0

... 然而,两参数双曲线模型只是在模型曲线形状与实测沉降变形曲线形状相似的基础上提出,预测结果通常偏大^[10] ...

2009

0.0

... 两参数指数曲线模型是基于一维固结理论建立的模型,只考虑了主固结沉降,而忽略了次固结沉降的影响,所以推算结果通常偏小^[11] ...

2008

0.0

... 3 传统模型沉降时程曲线特征大量试验数据表明,两个传统模型在拟合地基工后沉降时,既有拟合较为理想^[12]的情况,也有拟合较差^[13]的情况 ...

2017

0.0

... 3 传统模型沉降时程曲线特征大量试验数据表明,两个传统模型在拟合地基工后沉降时,既有拟合较为理想^[12]的情况,也有拟合较差^[13]的情况 ...

2008

0.0

王伟, 孙斌祥, 卢廷浩. 公路路堤软土地基工后沉降的三参数预估模型[J]. 中国公路学报, 2008, 21(2): 12-17.

WANG

Wei

, SUN

Binxiang

, LU

Tinghao

. 3-parameter prediction model of post-construction settlement for soft soil foundation under highway embankment[J]. China Journal of Highway and Transport, 2008, 21(2): 12-17. (in Chinese)

Combined with initial settlement rate and final settlement volume, half-value time of settlement is employed to build the mathematical property equations of post-construction settlement-time curve model for soft foundation under highway embankment. The mathematical deficiencies of exponential model and hyperbolic model were revealed. 3-parameter model for post-construction settlement-time was established based on energy dissipating assumption. Mathematical proof shows that the exponential model and hyperbolic model are up boundary and low boundary of the new established model respectively. Research results show that new established model overcomes the deficiencies of exponential model and hyperbolic model and its mathematic property satisfies the request of ideal settlement curves. The accuracy of the new model was proved by the engineering case.

1. Department of Civil Engineering, Shaoxing College of Arts and Sciences, Shaoxing 312000, Zhejiang, China; 2. Institute of Geotechnical Engineering, Hohai University, Nanjing 210098, Jiangsu, China

引入沉降半衰期的概念, 结合初始沉降速率、最终沉降量, 建立了路基工后沉降-时间曲线模型的数学特征方程, 揭示了传统指数模型和双曲线模型的数学缺陷。基于能量耗散假定, 建立了工后沉降-时间关系的三参数模型, 并从数学上严格证明了指数模型是三参数模型的上界, 双曲线模型是三参数模型的下界, 它们均是三参数模型的简化形式。研究结果表明:三参数模型性质与理想工后沉降曲线一致, 其克服了2种传统模型的不足。工程实测进一步证明了三参数模型的正确性。

... 式中:t_[1_/_2]为沉降半衰期,是指工后沉降量达到最终工后沉降量的50%时所对应的时间^[14] ...

2009

0.0

朱志铎, 周礼红. 软土路基全过程沉降预测的Logistic模型应用研究[J]. 岩土工程学报, 2009, 31(6): 965-969.

ZHU

Zhiduo

, ZHOU

Lihong

. Application of Logistic model in settlement prediction during complete process of embankment construction[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(6): 965-969. (in Chinese)

A large number of settlement observation data are analyzed and the laws of the development of settlement-time curve measured are studied.The settlement-time curve show the occurrence,development,stability,and then the limit of a certain form and that the form accords with the basic form of the growth curve.The entire process of settlement prediction model is established and the meaning of the parameters is analyzed.The influence of various parameters at different settlement stages and the application scope and its guiding significance in practice are analyzed.The evaluation of the model is ideal and the predicted results of several project examples show that the present model is scientific and applicable.

1.Institute of Geotechnical Engineering Southeast University Nanjing 210096 China 2.East China Electric Power Design Institute Shanghai 200331 China

通过大量观测数据分析,研究了高速公路软土地基沉降曲线发展规律,沉降历时曲线一般经过发生、发展、稳定后达一定极限,其表现形式符合成长曲线的基本形式。建立软土路基全过程沉降预测的Logistic模型,确定了模型中各参数含义,分析了各参数对地基沉降不同阶段的影响、应用范围及其在实践中的指导意义。给出模型的求解方式,讨论了模型预测效果,工程实例预测结果表明所建立模型具有科学性和适用性。

... ^[15]曲线与固结曲线的拟合度非常高,基于地基沉降是地基土压缩变形的宏观体现这一基本认识,且考虑地基工后沉降变形曲线过原点,故对#cod#x0201c ...

2017

0.0

... 18 mm范围内,远小于我国TB 10001—2016《铁路路基设计规范》要求的重载铁路路基工后沉降控制限值200 mm^[16],表明由粉质黏土和全风化软质岩组成的中等压缩性土地基在一般路堤荷载作用下的工后沉降能满足重载铁路路基沉降控制的要求 ...