基于人工蜂群算法的存储负载副本放置均衡算法

引用本文

郭佳, 马朝斌, 苗萌萌, 张绍博. 基于人工蜂群算法的存储负载副本放置均衡算法[J]. 北京交通大学学报, 2020,44(3): 142-148.
GUO Jia, MA Chaobin, MIAO Mengmeng, ZHANG Shaobo. Replica placement of storage load balancing algorithm based on artificial bee colony[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2020,44(3): 142-148.
Doi:10.11860/j.issn.1673-0291.20190133 复制到剪切板

Permissions

北京交通大学学报编辑部所有

基于人工蜂群算法的存储负载副本放置均衡算法

郭佳^1,², 马朝斌^1,², 苗萌萌², 张绍博²

1.北京交通大学计算机与信息技术学院,北京 100044

2.国家保密科技测评中心, 北京 100044

第一作者:郭佳(1983—),女,北京市人,博士生.研究方向为存储安全.email:m13581902161@163.com.

收稿日期: 2019-11-25

基金: 国家科技重大专项项目(2015ZX01029101)

摘要

针对固态盘闪存阵列中没有盘间损耗均衡策略,导致阵列中某些固态盘被更快损耗的问题,研究了存储盘间负载均衡的主要实现技术,分析了不同技术中具有代表性实现算法的优缺点,提出利用副本放置方法达到闪存阵列中盘间损耗均衡的策略,以及磁盘能量、数据负载能量和副本能量概念,分析得出磁盘能量与所要分配的副本之间属于NP(Non-deterministic Polynomial)-hard关系,利用马尔科夫链对人工蜂群算法(Artificial Bee Colony algorithm,ABC)进行改进并用以实现磁盘间的负载均衡.通过在Matlab上进行模拟仿真实验,比较了加权轮寻算法和改进ABC算法对副本在物理磁盘上的自动分配结果,并比较了改进ABC算法在不同运行次数和不同物理磁盘数量对结果运算精度也就是副本配置情况的影响.改进ABC算法可以较迅速地完成磁盘间副本分配并达到较好的分配效果.

关键词: 人工智能; 人工蜂群算法; 马尔科夫链; 副本放置; 负载均衡

中图分类号:TP181 文献标志码:A 文章编号:1673-0291(2020)03-0142-07

Replica placement of storage load balancing algorithm based on artificial bee colony

GUO Jia^1,², MA Chaobin^1,², MIAO Mengmeng², ZHANG Shaobo²

1. School of Computer and Information Technology, Beijing Jiaotong University, Beijing 100044,China

2. National Secrecy Science and Technology Evaluation Center, Beijing 100044,China

Fund:National Technology Key Project(2015ZX01029101)

Abstract

Targeting on the issue of absence of cross-disk loss balancing strategy of Solid State Disk(SSD) in Flash Array(FA) that leads to faster loss of certain SSDs in FA, this paper has studied main technologies for realization of cross-disk load balancing, analyzed strengths and weaknesses of representative realization algorithms of different technologies, proposed the use of replica placement for realization of cross-disk loss balancing strategy in FA, proposed the ideas of disk energy, data load-carrying energy and replica energy, analyzed NP-hard relationship between disk energy and replicas to be distributed, and used Markov Chain to improve ABC algorithm and realize cross-disk load balancing. It has compared results of automatic distribution of replicas on physical disk by weighted round-robin and improved ABC algorithm through running simulation experiment in Matlab, and compared improved ABC algorithm's impact on operation precision (replica configuration) with different running times and different numbers physical disks. The improved ABC algorithm can relatively rapidly finish distribution of replicas among disks, and yield better distribution results.

Keyword: artificial intelligence; artificial bee colony algorithm; Markov chain; replica placement; load balancing

文章图片

固态硬盘因其具有传统机械硬盘不具备的快速读写、质量轻、能耗低以及体积小等特点, 逐渐被广泛应用.因闪存有擦除次数限制, 所以采用内部的损耗均衡机制来保证块的损耗均匀, 但缺少盘间损耗均衡机制来保证系统中的所有硬盘都均匀地损耗, 当一块硬盘达到损耗极限而失效时, 替换及重构该盘上的数据会耗费很多时间和资源, 随着固态盘容量的不断增大, 这个消耗将会进一步增长, 影响整个系统的可靠性和可用性.

负载均衡技术主要包括数据分片、数据放置优化、数据迁移以及多副本下动态请求分发4类.数据分片和数据放置优化方法实现简单, 如文献[1]提出的静态非分区文件分配策略SOR, 尽可能减少同一节点上文件间的大小差异, 以减少系统的平均响应时间, 但这种优化只有在文件写入时才被触发, 属于被动优化; 在数据迁移方面, 人工智能的经典算法被引用, 如文献[2]提出的基于遗传算法、文献[3]提出的基于改进遗传算法及文献[4]提出的基于LSBPSO算法均可以解决磁盘的负载不均衡问题, 但数据迁移需要将已经存入的数据进行再次搬迁, 增加了系统运行负担; 在多副本下动态请求分发方面, 文献[5]提出选择最轻载且存有数据副本的节点进行数据访问, 文献[6]等提出基于数据迁移的动态副本管理算法CDRM, 文献[7]通过对热度高的数据创建新副本并将其放置在负载较轻的节点上以减少访问响应时间, 文献[8]提出将放置节点组织成树型结构, 对负载均衡和副本数量进行研究, 生物智能算法在副本均衡方面也有一定研究, 蚁群算法^[9]粒子群算法^[10]和萤火虫算法^[11]均被用于解决存储系统副本的问题.

本文作者结合存储系统副本放置方法, 改进ABC算法并将其用于均衡磁盘间的负载, 实现了磁盘间动态的负载能量调整.

1 副本放置模型

本文主要基于数据负载及其副本的异构特性和不同磁盘性能的异构性, 将问题表述为如何选择合适的磁盘放置副本, 在处理数据副本访问的同时保证存储系统整体开销最小化.

定义1 定义存储系统中物理磁盘的集合P表示为 $\{p_{1}, p_{2}, \dots, p_{n}\}$ , n为物理磁盘的总数, p_i∈ P表示一个磁盘元素.

定义2 定义数据集合F为映射到所有物理磁盘上的数据负载集合, 表示为 $\{f_{1}, f_{2}, \dots, f_{m}\}$ , m表示数据的总数, f_j∈ F表示一个数据负载.

定义3 定义数据集合V为映射到所有物理磁盘上的数据集合, 表示为 $\{v_{1}, v_{2}, \dots, v_{k}\}$ , k表示数据副本的总数, v_k∈ V表示一个负载副本.

定义f_j的能量e_f与数据负载大小和访问热度的函数关系, 在文件大小不变的前提下, 访问热度不同, 数据负载能量会随时间变化, 表示为

$e_{f} (t_{r}) = α \cdot e_{f} (t_{r - 1}) + β \cdot e_{f} (t_{0})$ (1)

$e_{f} (t_{0}) = \frac{d_{j}}{\overset{m}{\sum_{j = 1}} d_{j}}$ (2)

式中:d_j为数据f_j的负载大小; e_f(t₀)为对负载f_j的归一化处理结果, 代表没有进行任何访问时的文件初始能量; r为系统的运行时间; α 、β 为在时间集合T $\{t_{1}, t_{2}, \dots, t_{r}\}$ 上的衰减基数, 用来适应存储系统的实际需要, 比如在新投入使用且容量较小的存储系统中, 权值β 应设定的稍大, 在已经使用了一段时间且存储容量比较充裕的存储系统中, 权值α 应设定的稍大.

定义副本负载v_k的能量e_v与数据负载能量e_f的函数关系, 副本负载能量会随数据负载能量不同而变化, 同时随着时间的变化而衰减, 可按如下表示为

$e_{v} (t_{r}) = δ \cdot e_{f} (t_{r}) + η \cdot e_{v} (v_{j}, t_{r - 1})$ (3)

$e_{v} (t_{0}) = δ e_{f} (t_{0})$ (4)

式中:δ 、η 为调整参数.

在副本分配问题中, 物理磁盘p_i的能量包括数据负载和负载的副本两部分, 副本分配的前提是数据负载已经落盘完毕, 之后磁盘能量函数随着数据副本的存入, 可用存储空间逐渐变小, 物理磁盘能量变小, 其能量函数为

$E (p_{i}, t_{r}) = E_{s} (p_{i}, t_{r}) - \overset{m}{\sum_{j = 1}} e_{v} (t_{r}) - \overset{k}{\sum_{j = 1}} e_{f} (t_{r})$ (5)

$E_{s} = c w_{i}$ (6)

式中:c为调节参数, 用以表示磁盘在没有负载情况下的能量; w_i为磁盘容量; m为物理磁盘p_i存储的数据负载个数.实际分配到p_i上的数据负载及副本越小、磁盘性能越强, 则物理磁盘能量越大.

负载分配问题可以定义为存在一个映射f, 使得物理磁盘在时间t内总的能量均方差达到最小, 如下

$\varepsilon \left( {{f}_{V\to P}},t \right)=\sqrt{\frac{1}{n-1}\overset{n}{\mathop{\underset{i=1}{\mathop{\sum }}\,}}\,{{[\overline{E\left( {{p}_{i}},t \right)}-E({{p}_{i}},t)]}^{2}}}$(7)

$\overline{E\left( {{p}_{i}},t \right)}=\frac{\overset{n}{\mathop{\underset{i=1}{\mathop{\sum }}\,}}\,E\left( {{p}_{i}},t \right)}{n}~$(8)

定理1 基本的负载均衡算法使得副本按照磁盘的存储能量均衡地分布在不同磁盘上, 即某个磁盘上的所有数据负载能量与副本能量的和与其存储能量大小成正比.

证明文献[12]的定理6指出, 一个数据元素分配给某个节点的概率等于节点的相对权重.在基本的磁盘存储过程中, 单位时间内, 每个副本能量对应一个数据元素, 物理磁盘相当于节点, 因此一个副本分配给磁盘的概率等于其相对的存储能量, 所以数据的负载按照磁盘的存储能量公平地分布.

根据以上分析可以看出副本分配均衡问题属于数据放置问题, 即经典的FAP(File Assignment Problem), FAP已经被文献[13]证明是NP-hard问题, 很多学者已经提出利用人工蜂群算法解决NP-hard问题^{[14, 15]}, 因此本文提出改进的人工蜂群算法, 实现数据负载副本的自动均衡.

2 副本放置算法

人工蜂群算法由土耳其学者D.Karaboga于2005年提出, 具有操作简单、控制参数少、搜索精度高和鲁棒性强的特点^[16], 已成功应用于人工神经网络训练、系统工程设计^{[17, 18]}、组合优化^[19]等多个领域.

人工蜂群算法用蜜源的位置表示解, 用蜜源的蜂蜜量表示适应值.将蜜蜂分为雇佣蜂、跟随蜂和侦察蜂.算法步骤如下:

1)初始阶段.确定蜜源数量S_N, 解空间维度D, 雇佣蜂数量与蜜源数量一致.蜜源X_i= $(x_{i 1}, x_{i 2}, \dots, x_{iD})$ 代表一个候选解, 其中i∈ $\{1, 2, \dots, S_{N}\}$ .蜜源范围为 $[{X_{\min}}^{}, {X_{\max}}^{}]$ , 生成初始蜜源为

$X_{i, j} = X_{j \min}^{} + φ_{ij} (X_{j \max}^{} - X_{j \min}^{})$ (9)

式中:φ _ij∈ (-1, 1), j∈ $\{1, 2, \dots, D\}$ , 每次求解后, 通过适应度函数判断解的优劣为

$f_{it} = \{\begin{array}{l} \frac{1}{1 + f (x_{ij})}, f (x_{ij}) \geq 0 \\ 1 + |f (x_{ij})|, f (x_{ij}) < 0 \end{array}$ (10)

2)雇佣蜂阶段.雇佣蜂负责探索蜜源, 在蜜源附近, 产生一个随机的候选解为

$V_{ij} = X_{ij} + φ_{ij} (X_{ij} - X_{kj}), i \neq k$ (11)

式中:X_kj为随机选取的不同于X_ij的另一个蜜源, k∈ $\{1, 2, \dots, S_{N}\}$ .通过贪婪选择决定是否由V_ij替换X_ij.

3)跟随蜂阶段.跟随蜂接收雇佣蜂的蜜源信息后进一步进行开采.通过轮盘赌算法, 根据蜜源的适应度f_it按式(12)计算蜜源被选中的概率P_i, 适应度越高, 被选中的概率越大.

$P_{i} = \frac{f_{it,_{i}}}{\sum_{i = 1}^{S_{N}} f_{it,_{i}}}$ (12)

4)侦察蜂阶段.当一个蜜源达到开采上限L_imit时适应度仍未更新, 蜜源被淘汰, 根据式(9)随机选取新蜜源.

2.1 确定适应度函数

适应度函数是评价人工蜂群算法优劣的标准, 直接反应个体性能.根据磁盘能量变化特点, ε 为大于0的值, 故本算法的适应度函数定义为

$f_{it} = \frac{B}{A + ε}$ (13)

式中:A、B为加权系数, 这两个值均可根据实际情况设定.

2.2 生成初始种群

解空间是一个三维变量, 3个维度分别代表蜜源数量I、解的维度J和迭代步数T, 初始情况下T=1, 解空间可以表示为

$X = [\begin{array}{l} x_{11} & x_{12} & ... & x_{1 J} \\ x_{21} & x_{22} & ... & x_{2 J} \\ ... & ... & ... & ... \\ x_{I 1} & x_{I 2} & ... & x_{IJ} \end{array}]$ (14)

式中:x_ij=e_f(f_ij), 代表数据的负载能量, i∈ $\{1, 2, \dots, I\}$ , j∈ $\{1, 2, \dots, J\}$ , 解空间维度i为蜜源的数量, 表示物理磁盘, 解空间维度j表示X_i上存储的数据负载个数, 也就是一个物理磁盘上分布的每一个数据负载能量, 雇佣蜂数量与蜜源数量一致, 没有分配负载的元素标记为0.

按照负载能量分配情况计算得出副本分配前的数据负载分配方案, 也就是副本放置前磁盘的能量情况, 记为E_s(p_i), 在此后的求解过程中E_s(p_i)不改变.

数据负载能量分配完成后, 进一步按照E_s(p_i)的大小对副本文件进行分配, E_s(p_i)大的磁盘分配能量值e_v比较小的副本.

2.3 改进ABC算法

用改进ABC算法(I-ABC)实现副本均衡, 数据负载分配之后就是副本的均衡过程, 在副本分配过程中x_ij=e_f+e_v, 代表数据的负载和副本总能量, 分配过程可分为3个步骤.

2.3.1 雇佣蜂阶段

ABC算法在雇佣蜂阶段按式(11)生成新的解, 但想要达到磁盘负载均衡的目的, 仅需把不同磁盘间已有的数据负载能量进行交换, 完成迁移.故改进的算法在雇佣蜂阶段不是生成新的v_ij, 而是随机生成第i个解的第j维分量和其他解k的任一维分量l, 将x_ij与x_kl交换位置.k∈ $\{1, 2, \dots, S_{N}\}$ , l∈ $\{1, 2, \dots, D\}$ , 通过式(13)判断解的优劣后根据贪婪选择算法决定是否交换, 按时步记录每次更新后的解空间值.

2.3.2 跟随蜂阶段

跟随蜂接收雇佣蜂的蜜源信息后进一步进行开采.通过轮盘赌算法, 根据蜜源的适应度计算蜜源被选中的概率, 适应度越高, 被选中的概率越大.在I-ABC算法运行的第1阶段, 被选的蜜源直接与随机选取的另一个蜜源进行交换, 按时步记录每次更新后的解空间值.在运行ω 次ABC算法后, 算法进行第2阶段, 解空间为加入运行次数的三维解空间X_t=(X₁, X₂, ..., X_ω), 此时, 将Markov方法加入寻优过程, 改进ABC算法的跟随蜂阶段, 具体步骤如下:

1)划分状态空间.通过轮盘赌算法, 根据蜜源的适应度计算蜜源被选中的概率, 将被选中蜜源x_ij在t维度的所有解, 也就是根据副本负载能量大小, 按照时步进行排序, 最先产生的解在前面, 再划分状态空间, k个副本, 如需划分n个状态空间, 则每个状态空间的边界值为

$L (x_{ij}, t) = {x_{ij, \min}}^{} (t) + \frac{k - 1}{n} [{x_{ij, \max}}^{} (t) - {x_{ij, \min}}^{} (t)]$ (15)

式中:x_ij=e_v(f_ij); x_ij_, ${_{\min}}^{}$ (t)和x_ij_{, max}(t)分别代表t个时步内解空间X_ij=(x_ij₁, x_ij₂, …, x_ijt)的最小值和最大值, t=(ω , ω +1, …, M-1), M为最大循环次数.

2)计算转移概率矩阵, 将解X_ij放入对应的状态空间, 计算不同解所处状态空间的转移次数, 进一步得出不同转移步数对应的状态转移概率矩阵.

3)预测下一时步解所在的状态空间, 确定参与预测的最近时步步数, 提取不同步数概率转移矩阵中所处状态空间对应的行向量, 组成预测矩阵, 将预测矩阵列向量的概率值相加, 最大概率值对应的状态空间即为下一时步解可能落入的状态空间.

4)生成新的解空间, 在解空间中找到处于这个预测状态空间的解x_kl(t), 与x_ij(t)进行交换, 通过式(13)适应度函数判断解的优劣, 然后通过贪婪选择算法决定是否进行最终交换.

2.3.3 侦察蜂阶段

当一个蜜源达到开采上限L_imit时适应度仍未更新, 蜜源被淘汰, 并随机选取新蜜源, 选取新蜜源后再与随机选取的另一个蜜源进行交换, 按时步记录每次更新后的解空间值.

2.4 算法终止条件

ABC算法本身的终止条件有两个:1)目标值达到预设精度ε , 使其小于或等于预设值; 2)循环达到预设次数M值时停止.

2.5 函数伪代码

主函数伪代码如下所示:

INITIAL

设置初始值I、L_imit、J、M;

将负载能量分配至磁盘P[S_N], 生成初始解空间Foods[S_N, D, 1]

按式(10)计算f_it

计算负载总能量SumFoods、物理磁盘总能量SumP

I-ABC

while(t< M)

for i=1:(I× J)

交换Foods(i, j)和Foods(k, l), 计算f'_it

if (f'_it> f_it), 将交换后的解记入Foods[S_N, D, t]

蜜源更新次数trial=0

else, trial=trial+1

end

prob=0.9* f_it/(f_it+0.1)

a=1、b=0

while(t< I× J)

if(rand< prob),

b=b+1;

While(t< ω )

交换Foods(i, j)和Foods(k, l), 计算f'_it

While(ω < =t< M)

依式(6)计算状态空间边界值

计算状态空间转移次数

计算状态空间转移频率矩阵预测下一时步解所处状态空间S

找到值属于S的Foods(k, l)

交换Foods(i, j)和Foods(k, l), 计算f'_it

end

if(f'_it> f_it), 将交换后的解记入Foods[S_N, D, t]

trial=0

else, trial=trial+1

end

a=a+1

if (a=( I× J)+1), a=1

End

end

if (有蜜源i开采次数> L_imit)

交换Foods(i, j)和Foods(k, l), 计算f'_it

if(f'_it> f_it), 将交换后的解记入Foods[S_N, D, t]

end

3 模拟预测实验

实验运行平台为OS:Windows 10(15063.1955), CPU:Intel(R) Core(TM)i7-7700HQ CPU 2.80 GHz, 内存:32.0 GB, 编程环境:Matlab R2016b.

3.1 磁盘分配结果比较

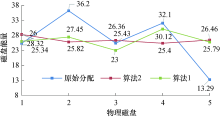
将加权轮寻算法定义为算法1, 本文的I-ABC算法定义为算法2, 比较不同算法之间的负载能量分配方案.选取5块物理磁盘(F_N), 20个数据负载(DF_N), 副本放置均衡后磁盘能量情况见图1.

	Figure Option View Download New Window
	图1 不同算法运行下磁盘能量Fig.1 Disk energy after running different algorithms

如图1所示经本文改进的I-ABC算法后, 磁盘能量间的均衡情况有明显提升.

3.2 不同循环次数对精度的影响

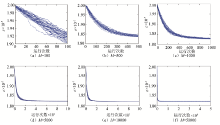
设定解空间维度D=100、蜜源数量F_N=3, 分别测试不同M下的物理磁盘负载均衡值.运行30次, 取其平均值, 不同循环次数下物理磁盘总能量的均方差值如表1所示, 不同循环次数对各磁盘结果精度的影响如图2所示.

表1 不同循环次数物理磁盘总能量均方差值 Tab.1 Mean variance of physical disk energy for different cycling numbers

	Figure Option View Download New Window
	图2 不同循环次数对各磁盘结果精度的影响Fig.2 Effects of different operational numbers on the results accuracy

由表1和图2可以看出, 随着算法运行次数的增加, 适应度值逐渐增加, 磁盘分配趋于合理.同时也可以看出, 随着次数的增加, 函数收敛速度减慢, 当算法运行5 000次后, 在10^-6数量级上精度一致.

3.3 不同物理磁盘数量对精度的影响

与3.2节参数设置一致, 负载初始值也一致, 取循环次数为500进行实验, 分别测试不同物理磁盘个数对磁盘负载均衡值的影响, 运行30次取其平均值.

通过表2和图3可以看出, 物理磁盘数量增大时算法可以自动进行调节, 实现动态的资源分配, 且磁盘数量越多, 负载均衡值越小, 各磁盘间的负载能量越均衡.

表2 不同数量物理磁盘总能量均方差值 Tab.2 Mean variance of physical disk energy for different disk numbers

	Figure Option View Download New Window
	图3 不同物理磁盘数量对结果精度的影响Fig.3 Effects of different numbers of physical disks on the results accuracy

4 结论

1)通过分析已有的副本放置的方法中所存在的不足, 提出了通过I-ABC算法对副本进行均衡放置的方法, 有效地实现了数据负载的动态分配, 实验验证得出算法在结果精度上有一定提升.

2)提出的算法仅能在已经生成的副本数量前提下进行动态平衡调整, 不能做到动态的增减副本数量.

下一步将继续对数据副本的最优生成条件和磁盘空间动态可变情况进行研究, 结合人工神经网络, 实现副本数量和放置位置相结合的均衡分配.

参考文献

文献列表

[1]	XIE T, SUN Y. A file assignment strategy independent of workload characteristic assumptions[J]. Acm Transactions on Storage, 2009, 5(3): 1-24. [本文引用:1]
[2]	董欢庆, 李战怀. 基于遗传算法的RAID磁盘阵列中磁盘负载均衡方法[J]. 计算机工程与应用, 2003(16): 41-43. DONG Huanqing, LI Zhanhuai. Disk load balancing method for RAID disk array based on the genetic algorithm[J]. Computer Engineering and Applications Comput Eng Appl, 2003(16): 41-43. (in Chinese) [本文引用:1]
[3]	倪云竹, 李志蜀, 胡大裟. 基于改进型遗传算法的存储子系统动态负载均衡[J]. 中南大学学报(自然科学版), 2013, 44(8): 97-106. NI Yunzhu, LI Zhishu, HU Dasha. Solution of dynamic load balancing in storage subsystem based on improved genetic algorithm[J]. Journal of Central South University (Science and Technology) , 2013, 44(8): 97-106. (in Chinese) [本文引用:1]
[4]	葛洪伟, 宋超. LSBPSO算法在磁盘负载均衡问题中的应用[J]. 计算机工程, 2009, 35(4): 201-203. GE Hongwei, SONG Chao. Application of LSBPSO in disk load balance problem[J]. Computer Engineering, 2009, 35(4): 201-203. (in Chinese) [本文引用:1]
[5]	MACCORMICK J, MURPHY N, RAMASUBRAMANIAN V, et al. Kinesis: A new approach to replica placement in distributed storage systems[J]. ACM Transactions on Storage, 2009, 4(4): 1-28. [本文引用:1]
[6]	WEI Q, VEERAVALLI B, GONG B, et al. CDRM: A cost-effective dynamic replication management scheme for cloud storage cluster[C]// Proceedings of the 2010 IEEE International Conference on Cluster Computing. Heraklion, 2010: 20-24. [本文引用:1]
[7]	CHEN L F, HONG D B. Adaptive data replicas management based on active data centric framework in cloud environment[C]//Proc of IEEE International Conference on High Performance Computing and Communications and IEEE International Conference on Embedded and Ubiquitous Computing. Zhangjiajie, 2013: 101-108. [本文引用:1]
[8]	WU J J, LIN Y F, LIU P F. Optimal replica placement in hierarchical data grids with locality assurance[J]. Journal of Parallel and Distributed Computing, 2008, 68(12): 1517-1538. [本文引用:1]
[9]	WANG L J, LUO J Z, SHEN J, et al. Cost and time ant colony algorithm for data replica in alpha magnetic spectrometer experiment[C]//Proc of IEEE International Congress on Big Data. Washington DC, 2013: 247-254. [本文引用:1]
[10]	LIM S P, HARSON H. Performance comparison of genetic algorithm, differential evolution and particle swarm optimization towards benchmark functions[C]//Proc of IEEE Conference on Open System. Piscataway, 2013: 41-46. [本文引用:1]
[11]	李君, 侯孟书. 基于萤火虫优化的副本放置方法[J]. 计算机应用研究, 2019, 36(2): 584-587. LI Jun, HOU Mengshu. Replica placement strategy based on glowworm swarm optimization[J]. Application Research of Computers, 2019, 36(2): 584-587. (in Chinese) [本文引用:1]
[12]	SCHINDELLHAUER C, NIXDORF H. Weighted distributed hash tables[C]// Seventeenth ACM Symposium on Parallelism in Algorithms & Architectures. Las Vegas, 2005: 218-227. [本文引用:1]
[13]	DOWDY W, FOSTER D. Comparative models of the file assignment problem[J]. Computing Surveys, 1982, 14(2): 287-313. [本文引用:1]
[14]	TASGETIREN M F, PAN Q K, SUGANTHAN P N, et al. A discrete artificial bee colony algorithm for the no-idle permutation flow shop scheduling problem with the total tardiness criterion[J]. Applied Mathematical Modelling, 2013, 37(10/11): 6758-6779. [本文引用:1]
[15]	WANG S, WANG P, et al. An artificial bee colony algorithm based optimization method for service: network customization[C]// International Conference on Service Sciences. Washington D C, 2013: 101-106. [本文引用:1]
[16]	KARABOGA D, ADAKAY B. A comparative study of artificial bee colony algorithm[J]. Applied Mathematics and Computation, 2009, 214(1): 108-132. [本文引用:1]
[17]	刘宏杰, 唐涛, 夏夕盛, 等. 面向再生制动能利用的地铁列车时刻表优化模型[J]. 北京交通大学学报, 2019, 43(1): 71-78. LIU Hongjie, TANG Tao, XIA Xisheng, et al. A timetable optimization model to maximize regenerative energy utilization in subway systems[J]. Journal of Beijing Jiaotong University, 2019, 43(1): 71-78. (in Chinese) [本文引用:1]
[18]	张辉, 赵鹏. 基于改进蜂群算法的城市公交网络设计[J]. 北京交通大学学报, 2015, 39(4): 118-124. ZHANG Hui, ZHAO Peng. Transit network design based on modified bee colony algorithm[J]. Journal of Beijing Jiaotong University, 2015, 39(4): 118-124. (in Chinese) [本文引用:1]
[19]	周炳海, 刘文龙. 考虑能耗的再制造系统多目标调度方法[J]. 哈尔滨工业大学学报, 2018, 50(7): 117-124. ZHOU Binghai, LIU Wenlong. Multi-objective scheduling algorithm for remanufacturing system considering energy consumption[J]. Journal of Harbin Institute of Technology, 2018, 50(7): 117-124. (in Chinese) [本文引用:1]

2009

0.0

... 数据分片和数据放置优化方法实现简单,如文献[1]提出的静态非分区文件分配策略SOR,尽可能减少同一节点上文件间的大小差异,以减少系统的平均响应时间,但这种优化只有在文件写入时才被触发,属于被动优化 ...

2003

0.0

董欢庆, 李战怀. 基于遗传算法的RAID磁盘阵列中磁盘负载均衡方法[J]. 计算机工程与应用, 2003(16): 41-43.

DONG

Huanqing

, LI

Zhanhuai

. Disk load balancing method for RAID disk array based on the genetic algorithm[J]. Computer Engineering and Applications Comput Eng Appl, 2003(16): 41-43. (in Chinese)

该文对RAID磁盘阵列内逻辑磁盘和物理磁盘之间的映射和负载关系进行分析,提出了一种基于遗传算法的物理磁盘间负载均衡方法,以提高磁盘阵列的吞吐量.仿真实验证明该方法是有效的.

... 在数据迁移方面,人工智能的经典算法被引用,如文献[2]提出的基于遗传算法、文献[3]提出的基于改进遗传算法及文献[4]提出的基于LSBPSO算法均可以解决磁盘的负载不均衡问题,但数据迁移需要将已经存入的数据进行再次搬迁,增加了系统运行负担 ...

2013

0.0

2009

0.0

葛洪伟, 宋超. LSBPSO算法在磁盘负载均衡问题中的应用[J]. 计算机工程, 2009, 35(4): 201-203.

Hongwei

, SONG

Chao

. Application of LSBPSO in disk load balance problem[J]. Computer Engineering, 2009, 35(4): 201-203. (in Chinese)

This paper uses Level-Set-Based Particle Swarm Optimizion(LSBPSO) to solve the problem of disk load balance. The characteristic of convergence of the algorithm swiftly adjusts the mapping between logic disk and physic disk which uses the technique of disk striping. It refers a new method to forecast the hot of logic disk and adds the content of expression of hot of physic disk. Simulation shows that the algorithm is efficient and defective.

(School of Information Engineering, Southern Yangtze University, Wuxi 214122)

将基于水平集的粒子优化算法(LSBPSO)应用于磁盘负载均衡问题中，利用LSBPSO的快速收敛性动态调整分条技术下逻辑磁盘和物理磁盘的映射关系。提出一种新的逻辑磁盘热度预测方法，对物理磁盘的热度的表示方法进行扩充。实验表明，LBPSO能较好地解决分条技术下的磁盘负载问题，收敛速度较快。

2009

0.0

... 在多副本下动态请求分发方面,文献[5]提出选择最轻载且存有数据副本的节点进行数据访问,文献[6]等提出基于数据迁移的动态副本管理算法CDRM,文献[7]通过对热度高的数据创建新副本并将其放置在负载较轻的节点上以减少访问响应时间,文献[8]提出将放置节点组织成树型结构,对负载均衡和副本数量进行研究,生物智能算法在副本均衡方面也有一定研究,蚁群算法^[9]粒子群算法^[10]和萤火虫算法^[11]均被用于解决存储系统副本的问题 ...

2010

0.0

2013

0.0

2008

0.0

2013

0.0

2013

0.0

2019

0.0

2005

0.0

... 证明文献[12]的定理6指出,一个数据元素分配给某个节点的概率等于节点的相对权重 ...

1982

0.0

... 根据以上分析可以看出副本分配均衡问题属于数据放置问题,即经典的FAP(File Assignment Problem),FAP已经被文献[13]证明是NP-hard问题,很多学者已经提出利用人工蜂群算法解决NP-hard问题^[14,15],因此本文提出改进的人工蜂群算法,实现数据负载副本的自动均衡 ...

2013

0.0

2013

0.0

2009

0.0

... Karaboga于2005年提出,具有操作简单、控制参数少、搜索精度高和鲁棒性强的特点^[16],已成功应用于人工神经网络训练、系统工程设计^[17,18]、组合优化^[19]等多个领域 ...

2019

0.0

2015

0.0

2018

0.0