基于温度-车辆荷载作用下沥青路面细观力学响应

引用本文

严战友, 王震, 陈嘉信, 盖惠恩, 王旭蕊. 基于温度-车辆荷载作用下沥青路面细观力学响应[J]. 北京交通大学学报, 2020,44(3): 118-128.
YAN Zhanyou, WANG Zhen, CHEN Jiaxin, GE Huien, WANG Xurui. Micromechanical response of asphalt pavement under temperature-vehicle load[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2020,44(3): 118-128.
Doi:10.11860/j.issn.1673-0291.20190077 复制到剪切板

Permissions

北京交通大学学报编辑部所有

基于温度-车辆荷载作用下沥青路面细观力学响应

严战友^1a, 王震^1b, 陈嘉信², 盖惠恩^1a, 王旭蕊^1a

1.石家庄铁道大学 a.土木工程学院,b.交通运输学院,石家庄 050043

2.河北大学质量技术监督学院,河北保定 071002

第一作者:严战友(1972—),男,河北遵化人,副教授,博士. 研究方向为车-路桥非线性动力学. email:yanzhanyou@163.com.

收稿日期: 2019-07-04

基金: 国家自然科学基金(111172183); 中央引导地方科技发展专项(18242219G); 河北省科技计划项目(15457605D,144576106D)

摘要

为了研究温度-车辆共同荷载作用下沥青路面各结构层细观力学响应,依据常用沥青路面各结构层材料级配及孔隙率建立了离散元模型,通过拟合室内单轴压缩应力-应变曲线获取模型的细观参数.在此基础上,对车辆荷载和不同温度作用下的沥青路面响应进行求解,分析各结构层细观力学响应及结构层颗粒变化情况.研究结果表明:在移动荷载及温度共同作用下,随着路面结构层深度增加,垂向位移逐渐降低,温度越高垂向位移越大;各结构层垂向应力随路面深度增加而依次减小;水平方向各结构层应力情况复杂,上面层处于受压状态,其余结构层颗粒既有受压也有受拉状态;切向应力处于拉应力与压应力交替状态,温度对颗粒应力影响较大;颗粒前期速度振动较为剧烈,后期速度振动较为平缓.

关键词: 离散元模型; 车辆模型; 温度荷载; 移动荷载; 应力

中图分类号:U441.3 文献标志码:A 文章编号:1673-0291(2020)03-0118-11

Micromechanical response of asphalt pavement under temperature-vehicle load

YAN Zhanyou^1a, WANG Zhen^1b, CHEN Jiaxin², GE Huien^1a, WANG Xurui^1a

1a. School of Civil Engineering, 1b. School of Transportation Engineering,Shijiazhuang Tiedao University, Shijiazhuang 050043,China

2. College of Quality and Technical Supervision, Hebei University, Baoding Hebei 071002, China

Fund:National Natural Science Foundation of China (111172183); The Central Government Guides Local Science and Technology Development(18242219G); Science and Technology Plan Project of Hebei Province (15457605D,144576106D)

Abstract

In order to study the micromechanical response of each structural layer in asphalt pavement under temperature-vehicle load, a discrete element model is established based on the material gradation and porosity of each structural layers of common asphalt pavement. The mesoscopic parameters of the model are obtained by fitting the indoor uniaxial compression stress-strain curve. On this basis, the response of asphalt pavement under vehicle load and different temperatures is obtained, and the microscopic mechanical response and particle changes of each structural layer are analyzed. The research results show: under the combined action of moving load and temperature,as the depth of the pavement structure increases,the vertical displacement gradually decreases, and the higher the temperature, the longer the vertical displacement;the vertical stress of each structural layer decreases with the increasing pavement depth; the horizontal stress of each structural layer is complex, as the upper layer is compressed, and the particles in the remaining structural layers are in mixed states of compression and tension; the tangential stress alternate from tensile stress to compressed stress, and temperature has a great impact on particle stress; the velocity vibration is more severe in the early stage of the particle, while the vibration weakens in the later stage.

Keyword: discrete element model; vehicle model; temperature load; moving load; stress

文章图片

沥青路面作为目前广泛使用的路面材料, 其内部由不同的沥青、粗集料、细集料及矿粉组成, 导致沥青路面结构是一种非均质、非连续体.在外界车辆荷载作用下, 其路面内部材料的应力-应变也是不连续的.因此, 从宏观角度将沥青路面简化为均匀连续介质的研究方法, 无法反映路面结构内部受力及变形的真实性.目前, 很多学者从细观角度对沥青路面进行分析逐渐成为研究方向之一^{[1, 2]}.

有限元理论主要将路面结构简化为连续均匀介质, 从宏观角度分析了路面的力学行为, 体现在路面承载力大小、结构内部应力及位移量等.离散元理论认为路面各结构层是由若干大小、形状不同的颗粒组成, 离散元法将颗粒视为刚体, 通过颗粒间的重叠量计算接触力及位移变化量.离散元法研究沥青路面力学响应具有一定优势, 首先, 采用离散元法能够体现青混合料非匀质、非连续体的非线性力学特性; 其次, 通过离散元法建立模型不仅可以分析其宏观力学响应, 而且能够进一步探究结构内部颗粒的细观变化情况.

国内外专家学者针对于沥青混合料细观力学进行了一系列研究, 文献[3]模拟了单轴压缩试验, 结果表明, 随轴向应变的增加, 颗粒之间的接触压力个数逐渐减小, 接触拉力个数逐渐增大, 且颗粒之间的接触力均值先增加后减小.文献[4]通过实验获取模型细观参数, 建立了沥青混合料小梁实验模型, 将虚拟实验结果与室内实验对比, 其结果基本一致, 表明离散元法虚拟疲劳试验方法可以作为沥青混合料疲劳性能分析的辅助手段.文献[5]基于离散元方法进行了沥青混合料劈裂试验模拟, 表明采用DIP-FEM方法能将沥青混合料的微观结构和宏观力学性能结合起来.文献[6]通过建立上面层沥青路面模型, 分析了沥青混合料骨架特性, 骨架承受加载力的70%~80%, 对应力传递的贡献率达70%以上.文献[7]利用离散元法建立沥青混合料试件, 研究了集料及砂浆随时间的变化情况, 并于实测值进行对比验证, 其结果基本一致, 表明该方法具有一定可行性.文献[8]对黏弹性状态的沥青混合料进行单轴压缩实验, 通过测得蠕变柔量计算沥青混合料松弛模量, 用于预测沥青路面的黏弹性响应.文献[9]通过离散元法对黏性土类材料进行了平面双轴压缩试验模拟.结果表明, 颗粒黏结强度与材料黏聚力呈线性关系, 颗粒摩擦系数与材料内摩擦角呈对数关系.文献[10]建立了双层车辙试件模型, 分析了试件内部接触力变化及颗粒空间运动轨迹, 结果表明, 上面层主要受压, 拉应力则主要分布在下面层, SMA-13骨架性能比AC-20好.文献[11]采用Burgers本构关系开展了车辙变形细观模拟, 研究了骨料分布、荷载、温度等对车辙深度的影响, 结果表明, 当超载和高温共同作用时, 车辙变形会大幅度增加.文献[12]研究分析了沥青混合料半圆弯曲断裂的开裂机理, 发现法向和切向接触力在裂缝产生中都具有显著作用.文献[13]对混凝土的热膨胀系数性能进行了研究, 证实了细观力学方法的有效性.文献[14]利用PFC3D进行了沥青混合料的离析及级配模拟, 证明了通过离散元法进行沥青路面压实模拟探究细观行为是合理可行的.文献[15]通过对比路面细观数值模型与均质模型, 验证了细观状态下分析路面受力情况的有效性.

综上所述, 针对沥青路面结构细观力学行为的研究基本采用小尺度试件室内试验与模拟仿真相结合的方法, 对小尺度试件进行力学试验只能局部的分析其力学响应, 将局部力学响应放大至整个路面结构缺乏说服力.因此, 对整体沥青路面结构进行细观力学行为研究具有一定意义.

本文作者根据车-路相互作用理论, 依据实际路面各结构层级配及孔隙率, 通过拟合各结构层单轴压缩实验曲线获取模型细观参数, 应用离散元法构建大尺度路面结构模型, 在不同温度及二自由度1/4车辆荷载作用下, 计算沥青路面各结构层细观力学响应及各结构层颗粒移动状况.一方面可以为车-路相互作用研究提供新的思路, 即不但可以求解路面宏观力学响应, 也可以求解颗粒移动规律; 另一方面颗粒移动规律可以为路面结构层设计提供参考.

1 建立车-路相互作用模型

1.1 沥青路面离散元模型

为反映沥青路面力学响应, 根据相关文献, 采用传统沥青路面结构形式, 按照级配及孔隙率大小建立粗集料随机分布的二维路面离散元模型.模型分为上面层、下面层、上基层、下基层、底基层、路基层6部分.各结构层参数见表1.

表1 沥青路面各结构层参数 Tab.1 Structural parameters of asphalt pavement

地基层无限延伸, 其中路床主要用于承受及分散车辆荷载, JTG D30—2015《公路路基设计规范》^[16]中规定路床深度80 cm, 80 cm以外的地基深度对沥青路面力学响应影响较小, 同时为减小计算工作量, 本文地基层采用厚度为80 cm.建立沥青路面二维离散元模型, 见图1.

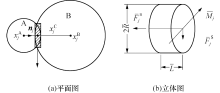
	Figure Option View Download New Window
	图1 沥青路面二维离散元模型Fig.1 Two-dimensional discrete element model of the asphalt pavement

由于路面模型较大, 为避免繁琐的多接触模型, 本文采用简单易行且可以反映路面结构内部颗粒受力及位移变化的线性平行黏结接触模型.平行黏结接触模型颗粒间接触原理见图2.

	Figure Option View Download New Window
	图2 线性平行黏结模型Fig.2 Linear parallel bond model

离散元软件通过相互接触颗粒间重叠量计算接触力的大小, 图2中 ${x^{A}}_{j}$ 、 ${x^{B}}_{j}$ 分别为颗粒A、B中心; ${x^{C}}_{j}$ 为接触颗粒中心; $\bar{R}$ 为接触颗粒半径; $\bar{L}$ 为接触颗粒长度; n_j为第j个接触的法向向量; ${\overset{̅}{M}}_{j}$ 为力矩.黏结力为

${\overset{̅}{F}}_{j} = {\overset{̅}{F}}_{j}^{n} + {\overset{̅}{F}}_{j}^{s}$ (1)

式中: ${\overset{̅}{F}}_{j}$ 为第j个接触的黏结力; ${\overset{̅}{F}}_{j}^{n}$ 为第j个接触的法向黏结力; ${\overset{̅}{F}}_{j}^{s}$ 为第j个接触的切向黏结力.

当颗粒之间产生力及位移时, 公式如下:

$Δ {\overset{̅}{F}}_{j}^{n} = (- {\overset{̅}{k}}^{n} AΔ u_{n}) n_{j}$ (2)

$Δ {\overset{̅}{F}}_{j}^{s} = - {\overset{̅}{k}}^{s} AΔ u_{s}$ (3)

$Δ M_{j}^{n} = - {\overset{̅}{k}}^{n} IΔ θ_{n}$ (4)

$Δ M_{j}^{s} = - {\overset{̅}{k}}^{s} IΔ θ_{s}$ (5)

${\overset{̅}{k}}^{n} = \frac{{\overset{̅}{k}}_{n}^{A} {\overset{̅}{k}}_{n}^{B}}{{\overset{̅}{k}}_{n}^{A} + {\overset{̅}{k}}_{n}^{B}}$

${\overset{̅}{k}}^{s} = \frac{{\overset{̅}{k}}_{s}^{A} {\overset{̅}{k}}_{s}^{B}}{{\overset{̅}{k}}_{s}^{A} + {\overset{̅}{k}}_{s}^{B}}$

式中: ${\overset{̅}{k}}^{n}$ 为法向接触刚度; A为接触面积; △u_n为法向位移距离; ${\overset{̅}{k}}^{s}$ 为切向接触刚度; △u_s为切向位移距离; I为接触面的转动惯量; △θ _n为颗粒相对法线的转角; △θ _s为颗粒相对切线的转角; ${\overset{̅}{k}}_{n}$ 为颗粒法向刚度; ${\overset{̅}{k}}_{s}$ 为颗粒切向刚度.

计算过程中, 通过以下公式对颗粒之间接触进行更新.

${\overset{̅}{F}}_{j}^{n} (t) = |{\overset{̅}{F}}_{j}^{n} (t - Δt)| n + Δ {\overset{̅}{F}}_{j}^{n}$ (6)

${\overset{̅}{F}}_{j}^{s} (t) = {\overset{̅}{F}}_{j}^{s} (t - Δt) + Δ {\overset{̅}{F}}_{j}^{s}$ (7)

$M_{j}^{n} (t) = |M_{j}^{n} (t - Δt)| n + Δ M_{j}^{n}$ (8)

$M_{j}^{s} (t) = M_{j}^{s} (t - Δt) + Δ M_{j}^{s}$ (9)

式中:△t为时间增量; n为法向向量.

通过更新后的接触力及力矩大小, 计算接触的法向及切向应力

$σ = \frac{- {\overset{̅}{F}}_{j}^{n}}{A} + \frac{M_{j}^{s}}{I} \bar{R}$ (10)

$τ = \frac{- {\overset{̅}{F}}_{j}^{s}}{A}$ (11)

初始模型平衡后, 内部接触清零.模型加载时, 通过不断更新模型颗粒间接触应力及位移, 添加测量圆, 测得各结构层响应情况.

1.2 车辆动力学模型

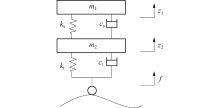
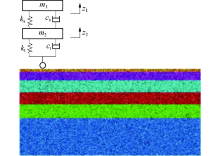
本文采用二自由度1/4车辆模型施加荷载, 车辆动力学模型如图3所示.

	Figure Option View Download New Window
	图3 车辆动力学模型Fig.3 Vehicle dynamic model

二自由度1/4车辆模型计算方程为

$\{\begin{array}{l} m_{1} {\ddot{z}}_{1} + c_{s} ({\dot{z}}_{1} - {\dot{z}}_{2}) + k_{s} (z_{1} - z_{2}) = 0 \\ m_{2} {\ddot{z}}_{2} - c_{s} ({\dot{z}}_{1} - {\dot{z}}_{2}) - k_{s} (z_{1} - z_{2}) + \\ c_{t} ({\dot{z}}_{2} - \dot{f}) + k_{t} (z_{2} - f) = 0 \end{array}$ (12)

式中:m₁、m₂分别为车体、轮胎质量; k_s、k_t分别为车体悬架、轮胎刚度; c_s、c_t分别为车体、轮胎阻尼系数; z₁、z₂分别为车体、轮胎垂向位移; f为路表不平度激励.

车辆模型计算参数见表2.

表2 车辆模型计算参数^[10] Tab.2 Calculation parameters of vehicle model^[10]

当研究车-路耦合相互作用时, 必须考虑路面对车辆的激励, 路面不平度可以引起车辆振动.本文采用GB/T 7031—86《车辆振动输入—路面不平度表示方法》^[17]中路面功率谱密度为

$G_{q} (v) = G_{q} (v_{0}) {(\frac{v}{v_{0}})}^{- w}$ (13)

式中:G_q(v)为路面功率谱密度; G_q(v₀)为参考空间功率谱密度; v为空间频率; v₀为参考空间频率, 取v₀=0.1, m^-1; w为频率指数, 一般取w=2.

路面不平度采用随机相位余弦叠加法, 具体式为

$r (x) = \overset{N}{\sum_{i = 1}} \sqrt[]{4 G_{q} (v) Δv} \cos (vx + θ_{i})$ (14)

式中:r(x)为路面不平度; x为路面纵向位置; G_q(v)为路面功率谱密度; △v为频率增量; θ _i为在0~2π 区间内均匀分布的随机相位角.

路面功率谱密度将不平度分为8个等级, 路面不平度等级系数G_q(v₀)下限、上限及几何平均值见表3.

表3 路面不平度系数 Tab.3 Coefficient of road roughness 10^-6m²/m^-1

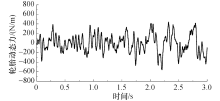
应用Matlab软件建立轮胎模型, 按照以上参数计算车辆行驶过程中产生的动荷载力, 得到轮胎动态荷载曲线, 见图4.

	Figure Option View Download New Window
	图4 轮胎动荷载曲线Fig.4 Dynamic load curve of the tire

2 颗粒流细观参数

由于沥青路面材料宏观参数不能直接应用于细观模型, 但宏观参数与细观参数之间有其相似性, 细观参数标定一般通过宏观力学应力-应变规律来寻求, 由于离散元模型中颗粒尺寸大小不同, 其细观参数也有一定差距.其中, 文献[18]通过试错法拟合标准单轴压缩试验从而获取细观参数, 本文也采用此方法, 沥青混合料单轴压缩应力-应变模拟试验与标准试验对比见图5, 其应力-应变曲线总体趋势相似, 此时模型参数作为相应结构层细观参数.

	Figure Option View Download New Window
	图5 SMA-13沥青混合料单轴压缩应力-应变模拟试验与标准试验数据对比Fig.5 Comparison of stress-strain curves between uniaxial compression simulated test and standard test of SMA-13 asphalt mixture

SMA-13型沥青混合料单轴压缩模拟试验见图6, 室内标准试验见图7.对比图6(b)与图7(b)可知, 宏观裂缝相似度较高, 说明该方法能够较好模拟沥青混合料结构体宏观力学变化, 则该方法模型细观参数具有一定合理性.

	Figure Option View Download New Window
	图6 SMA-13型沥青混合料单轴压缩模拟试验Fig.6 Uniaxial compression simulation test of SMA-13 asphalt mixture

	Figure Option View Download New Window
	图7 SMA-13型沥青混合料单轴压缩标准试验Fig.7 Uniaxial compression standard test of SMA-13 asphalt mixture

其余各层路面均采用相同方式进行细观参数获取, 不再赘述.路面各结构层材料细观参数见表4.

表4 路面各结构层材料细观参数 Tab.4 Microscopic parameters of materials for each structural layer of pavement

3 温度加载原理

根据傅里叶热传导定律.假设应变的变化对温度影响作用很小, 则连续体热传导方程为

$- \frac{\partial q_{i}}{\partial x_{i}} + q_{v} = ρ c_{v} \frac{\partial T}{\partial t}$ (15)

式中:q_i为热通量矢量, W/m²; q_v为体积热源强度或功率密度, W/m³; ρ 为质量密度, kg/m³; T是温度, ℃; c_v为恒定体积比热容, J/(kg· ℃).对于所有固体和液体, 恒定压力c_p和恒定体积下的比热基本相等, 因此, c_p和c_v可以互换使用.

热通量和温度梯度之间的关系为

$q_{i} = - k_{ij} \frac{\partial T}{\partial x_{j}}$ (16)

式中:k_ij是热导率张量, W/(m· ℃).

颗粒膨胀尺寸及温度变化关系为

$ΔR = α \overset{̅}{R} ΔT$ (17)

式中:α 为颗粒的线性膨胀系数; △T为温度增量; △R为颗粒半径增量.

假设黏结力的法向量受温度变化改变黏结键长度, 从而影响黏结的热膨胀, 法向黏结力变化为

△ ${\bar{F}}_{n}$ =- ${\bar{k}}_{n}$ A₁△U_n=- ${\bar{k}}_{n}$ A₁( $\bar{α} \bar{L}$ △T) (18)

式中: ${\overset{̅}{k}}_{n}$ 为黏结的法向刚度; A₁为黏结键的横截面积; $\overset{̅}{α}$ 为黏结材料热膨胀系数; △U_n为黏结键长度.

其中热量与导热率为

$Q = (k A_{1} ΔT) / D$ (19)

式中:Q为热量; k为导热率, W/(m·k); D为热量传递距离.

热阻值为

$η = (A_{1} ΔT) / Q$ (20)

式中:η 为热阻值.

本文采用沥青路面导热率0.699 W/(m·k), 路面初始温度为10 ℃, 路表温度设置为-20 ℃, 比热容为10^-5进行计算.

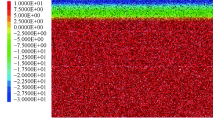
通过PFC内置热分析模块对二维沥青路面模型进行温度施加.温度自上而下加载, 主要是影响面层材料, 对基层材料的影响较小.施加温度后的路面模型见图8.

	Figure Option View Download New Window
	图8 施加温度后的路面模型Fig.8 Pavement model after warming

4 车辆模型移动载荷施加方式

车辆与路面相互作用时, 按照轮胎滚动形式施加车辆荷载难以确定其动态接触面积.因此, 本文将车-路接触面积设定为恒定值.车辆标准轴载设计参数见表5.

表5 车辆标准轴载设计参数 Tab.5 Design parameters for vehicles with standard axle load

根据文献[19], 将车辆轮胎简化为加载板进行加载, 假设轮胎接地面积为正方形, 长度为21.3 cm.加载力为

$B = \sqrt[]{\frac{P}{p}}$ (21)

式中:P为载荷力; p为接地胎压.

由于车辆加、减速情况复杂多变, 本文对匀速状态下路面各层力学响应进行分析.在路面左端建立轮胎(加载板)模型, 通过加载板对路面加载, 加载△t时间后, 删除最左侧一个颗粒单元, 同时在最右侧生成一个颗粒单元, 并对其施加外力, △t时间后继续删除-生成-加载步骤, 以此类推, 直至加载至模型右端结束.

颗粒单元加载时间由车辆行驶速度决定

$Δ t_{2} = 3.6 \times l / v_{2}$ (22)

式中:l为颗粒单元直径, 本文加载板单元颗粒1 mm; v₂为轮胎速度, 本文取v₂=60 km/h.

由于软件进行计算时, 自动计算合理时步, 因此需要通过设定循环次数以达到目标加载时间.循环次数计算式为

$c = Δ t_{2} / Δ t_{0}$ (23)

式中:c为循环次数; △t₀为软件自动计算得出的合理计算时步.

综上, 通过设定循环数c调整至目标车辆行驶速度, 对不同车速下路面响应问题也可以通过调整循环数与相应车速下动态加载力的方式进行分析.

车辆荷载由静载荷和动载荷两部分组成.车辆静载荷为25 kN, 动荷载见图4.对路面模型施加静荷载, 同时调用轮胎动荷载力, 实现车辆行驶过程中真实动态作用力的施加.车辆-路面离散元耦合模型见图9.

	Figure Option View Download New Window
	图9 车辆-路面离散元模型Fig.9 Discrete element model of the vehicle-pavement

本模型采用1/4车辆荷载(施加温度), 在颗粒流计算过程中, 实时对颗粒之间接触力与不平衡力进行平衡判断, 当模型中抗拉与抗剪切力超过材料黏结强度时, 模型会产生张拉与剪切微裂纹(模型自动统计微裂缝数量), 本模型结果没有出现微裂缝, 说明法向与切向应力没有超过容许值.

5 路面动力学响应

5.1 路面各结构层垂向位移

路面各结构层垂向位移-时间曲线见图10.从图10可以看出:在移动荷载和温度共同作用下, 路面各结构层内部出现一定量的挠度变形, 其中上面层、下面层、上基层、下基层、底基层、路基层的最大垂向位移分别为0.177、0.163、0.131、0.096、0.067、0.019 mm, 垂向位移随着路面结构层深度增加而减少.

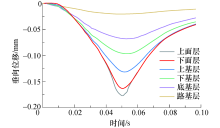	Figure Option View Download New Window
	图10 离散元路面各结构层位移时程曲线Fig.10 Displacement time-history curves of each structural layer of the discrete element pavement

由于缺乏离散元模型试验数据证明, 依据文献[20], 采用有限元软件建立二维路面模型, 其中, 在有限元模型中已经采用试验方法证明.有限元路面模型位移-时间计算曲线见图11.对比图10、图11, 其结果误差在5%, 线形大致相似.因此, 说明离散元法进行沥青路面力学分析具有一定可行性.

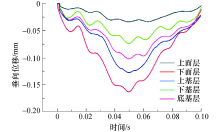	Figure Option View Download New Window
	图11 有限元路面各结构层位移时程曲线Fig.11 Displacement time-history curves of each structural layer of the finite element pavement

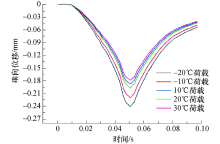
在不同温度-荷载作用下路表面垂向位移变化曲线见图12.从图12可以看出:当温度从-20 ℃增涨至30 ℃时, 其最大位移值分别为0.177、0.186、0.195、0.218、0.24 mm, 随着温度升高, 路表面垂向位移越来越大, 当外界温度升至30 ℃时, 其垂向挠度增加了35.6%, 说明温度对沥青混合料垂向挠度影响不可忽略.

	Figure Option View Download New Window
	图12 不同温度作用下位移时程曲线Fig.12 Displacement time-history curves of the pavement under different temperatures

5.2 路面各结构层应力响应

车辆荷载及温度共同作用下, 沥青路面各结构层内部产生一系列应力变化.本文主要从路面不同结构层垂向应力、水平应力和切向应力3方面进行分析.

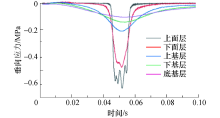
路面各结构层垂向应力随时间变化曲线见图13.从图13可以看出:车辆通过路面时, 路面各层中点处垂向应力几乎都是负值(受压状态), 其中上面层、下面层、上基层、下基层、底基层的最大垂向应力分别为0.632、0.477、0.207、0.141、0.104 MPa.数据说明:随着结构层深度的增加, 垂向应力越来越小, 上面层受到的垂向应力最大.

	Figure Option View Download New Window
	图13 路面各结构层垂向应力时程曲线Fig.13 Vertical stress time-history curves of structural layers of pavement

在不同温度-荷载作用下路表面垂向应力时程曲线见图14.从图14可以看出:当温度从-20 ℃增涨至30 ℃时, 其最大垂向应力值分别为0.63、0.67、0.75、0.78、0.83 MPa, 随着温度升高, 路表面垂向应力越来越大, 当外界温度升至30 ℃时, 其垂向应力增加了31.7%, 说明温度对垂向应力影响较大.高温状况对最大垂向应力响应所用时间较短, 低温状况对最大垂向应力响应所用时间较长.

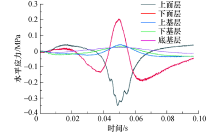
	Figure Option View Download New Window
	图14 不同温度垂向应力时程曲线Fig.14 Vertical stress time-history curves under different temperatures

沥青路面各结构层水平应力时程曲线见图15.从图15可以看出:在车辆荷载作用下, 路面各结构层的水平方向受力较复杂, 同时存在拉、压应力现象.上面层最大水平应力为0.345 MPa(压应力), 下面层、上基层、下基层、底基层的最大水平应力分别为0.205、0.04、0.03、0.02 MPa(拉应力), 线形呈对称布置.

	Figure Option View Download New Window
	图15 路面各结构层水平应力时程曲线Fig.15 Horizontal stress time-history curves of structural layers of pavement

上面层颗粒初始时刻处于受拉状态, 中间时刻处于受压状态, 结束时刻处于受拉状态; 由于下面层、上基层、下基层、底基层颗粒与车辆荷载没有直接接触, 其水平应力响应与上面层具有很大区别, 其水平应力变化趋势相似, 其中下面层颗粒开始时刻处于受拉状态, 随着时间延续, 颗粒逐渐处于受压状态-受拉状态-受压状态, 下面层颗粒变化比较复杂.上基层、下基层、底基层颗粒的水平应力变化小于下面层, 总体呈现受拉状态.

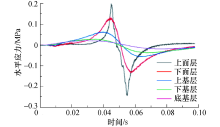
在不同温度-荷载作用下下面层水平应力变化曲线见图16.从图16可以看出:当温度从-20 ℃增涨至30 ℃时, 其最大水平应力值分别为0.205、0.197、0.177、0.165、0.149 MPa, 随着温度升高, 中面层最大水平应力逐渐减少, 当外界温度升至30 ℃时, 其水平应力减少了23.7%, 说明温度对水平应力影响较大.

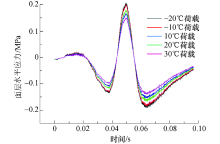	Figure Option View Download New Window
	图16 不同温度下面层水平应力时程曲线Fig.16 Horizontal stress time-history curves of surface layer under different temperatures

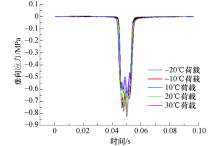
路面各结构层切向应力时程曲线见图17.从图17可以看出:车辆行驶过程中, 路面颗粒产生的水平切应力比较复杂, 当移动荷载逐渐接近测点位置时, 水平切应力逐渐增加(正值), 达到最大值后, 逐渐减少至零点, 当移动荷载碾压过测量位置时, 水平切应力也是逐渐增大(负值), 达到峰值之后逐渐较少, 即测量点的颗粒既经受拉应力又经受压应力, 线形几乎呈现反对称布置.上面层、下面层、上基层、下基层、底基层的最大拉应力分别为0.199、0.131、0.064、0.028、0.021 MPa, 其最大压应力分别为0.241、0.131、0.055、0.035、0.017 MPa, 切应力线形变化趋势总体相似, 随着路面深度增加, 其水平切应力呈现减少趋势.

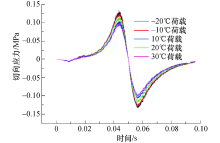
	Figure Option View Download New Window
	图17 路面各结构层切向应力时程曲线Fig.17 Tangential stress-time curves of structural layers of pavement

不同温度-荷载作用下的下面层切向应力变化曲线见图18.从图18可以看出:当温度从-20 ℃增涨至30 ℃时, 其最大切向应力值分别为0.131、0.121、0.110、0.100、0.090 MPa(拉应力), 随着温度升高, 中面层最大切向应力逐渐减少, 当外界温度升至30 ℃时, 其切向应力减少了31.3%, 说明温度对切向应力影响较大, 切向应力曲线呈现反对称布置.

	Figure Option View Download New Window
	图18 不同温度下面层切向应力时程曲线Fig.18 Tangential stress-time curves of the surface layer under different temperatures

5.3 路面各结构层颗粒移动状况

为了研究离散元模型中颗粒移动情况, 提取下面层中粗集料颗粒的垂向移动速度、水平移动速度及颗粒旋转速度.

不同温度作用下颗粒垂向移动速度曲线见图19.由图19可知:移动车辆荷载作用下, 在0~0.05 s时, 颗粒持续向下移动(负值), 此时, 车辆处于开始碾压阶段, 颗粒需要重新排列, 所以此阶段的颗粒上下振动比较厉害, 速度变化范围较大; 在0.05 s位置时, 车辆正好碾压观测点粗颗粒, 此时, 颗粒垂向移动速度几乎为零; 在0.05~0.10 s时, 车辆逐渐离开观测点颗粒, 则颗粒垂向移动速度变大(正值), 此时刻, 由于前端时间已经碾压离散元模型, 颗粒处于稳定状况, 所以此段曲线较前段曲线光滑, 当车辆完全离开模型时, 颗粒回归初始状态.当温度从-20 ℃增涨至30 ℃时, 颗粒竖向移动速度明显增大.垂向移动速度曲线几乎呈反对称布置.

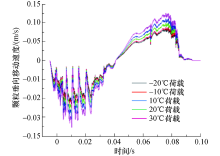	Figure Option View Download New Window
	图19 不同温度下颗粒垂向移动速度时程曲线Fig.19 Vertical moving speed time-history curves of the particles under different temperatures

不同温度作用下颗粒水平移动速度曲线见图20.由图20可知:移动车辆荷载作用下, 在0~0.05 s时, 颗粒处于初始碾压阶段, 颗粒需要重新排列, 则水平移动速度变化范围较大; 在0.05 s位置附近, 车辆正好碾压观测点粗颗粒, 此时颗粒水平移动速度几乎为零; 在0.05~0.10 s时, 车辆逐渐离开观测点颗粒, 由于前端时间已经使颗粒处于稳定状况, 所以水平移动速度变化范围远远小于前段时间.当温度从-20 ℃增涨至30 ℃时, 颗粒水平移动速度明显增大.

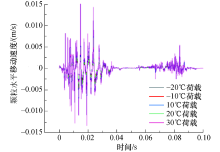	Figure Option View Download New Window
	图20 不同温度下颗粒水平移动速度时程曲线Fig.20 Horizontal moving speed time-history curves of the particles under different temperatures

不同温度作用下颗粒旋转速度曲线见图21.由图21可知:在0~0.05 s时, 颗粒处于初始碾压阶段, 颗粒需要重新排列, 则颗粒旋转速度变化范围较大; 在0.05 s位置附近, 车辆正好碾压观测点粗颗粒, 此时颗粒旋转速度逐渐降低; 在0.05~0.10 s时, 车辆缓慢离开观测点颗粒, 颗粒的旋转速度逐渐增加.当温度从-20 ℃增涨至30 ℃时, 颗粒的旋转速度明显增大.

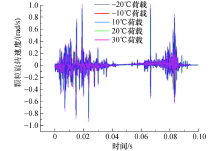	Figure Option View Download New Window
	图21 不同温度下颗粒旋转速度时程曲线Fig.21 Rotating speed time-history curves of the particles under different temperatures

由图19~图21可知, 温度对沥青混合料具有很大影响, 随温度升高, 颗粒体积增大, 颗粒弹性模量减小, 垂向应力有增大趋势, 切向应力及水平应力有减小趋势.温度升高导致沥青混合料骨料及砂浆颗粒间的黏结力降低, 颗粒约束减小, 垂向、水平方向颗粒振动加剧, 颗粒摆动幅度增大.

6 结论

通过建立1/4车辆及二维路基-路面离散元模型, 将外界温度变化施加于模型, 在温度-荷载共同作用下, 得到以下结论:

1)在移动车辆荷载作用下, 施加温度场可以获得模型内部颗粒流的力学响应, 其中垂向位移随着路面结构层深度增加而减少, 温度越高其垂向位移越大.

2)在移动车辆荷载作用下, 各结构层颗粒流的垂向应力随着深度增加而减少; 水平方向应力比较复杂, 上面层颗粒基本受压状态, 其余结构层颗粒既有受压也有受拉状态; 切向应力处于拉应力与压应力交替状态, 且随路面深度增加, 各结构层峰值逐渐减小.随着温度升高垂向应力呈现增大趋势, 其余应力呈现减少趋势.

3)在移动荷载作用下, 颗粒前期振动较为剧烈, 后期振动较为平缓, 颗粒随着温度升高其垂向、水平与转动方向上移动速度增大, 说明温度对离散元颗粒移动影响较大.

4)为了减少夏季高温对沥青混合料车辙及拥包等病害, 应从沥青混合料骨架结构、材料对温度敏感性、沥青砂浆黏聚力等方面进行选用.

基于离散元法对沥青路面进行温度-荷载作用下力学行为研究, 不仅能够反映沥青路面各结构层力学响应, 而且可以进一步分析结构内部颗粒变化情况.通过这种方法, 突破了以往宏观试验及小尺度试件的限制, 具有十分重要意义.从细观角度分析路面内部变化情况, 还需要更深层次的研究.

参考文献

文献列表

[1]	LIU Y, YOU Z P. Visualization and simulation of asphalt concrete with rand omly generated three-dimensional models[J]. Journal of Computing in Civil Engineering, 2009, 23(6): 340-347. [本文引用:1]
[2]	LIU Y, YOU Z P. Accelerated discrete clement modeling of asphalt-based materials with the frequency temperature superposition principle[J]. Journal of Engineering Mechanics, 2011, 137(5): 355-365. [本文引用:1]
[3]	侯曙光, 徐恺, 张浩. 基于离散元模拟的沥青混合料单轴压缩试验细观力学分析[J]. 南京工业大学学报(自然科学版), 2015, 37(5): 73-78. HOU Shuguang, XU Kai, ZHANG Hao. Micro-mechanical analysis of uniaxial compression test of asphalt mixtures by discrete element modeling[J]. Journal of Nanjing Tech University (Natural Science Edition), 2015, 37(5): 73-78. (in Chinese) [本文引用:1]
[4]	陈俊, 黄晓明. 基于离散元法的沥青混合料虚拟疲劳试验方法[J]. 吉林大学学报(工学版), 2010, 40(2): 435-440. CHEN Jun, HUANG Xiaoming. Virtual fatigue test of asphalt mixture based on discrete element method[J]. Journal of Jilin University (Engineering and Technology Edition), 2010, 40(2): 435-440. (in Chinese) [本文引用:1]
[5]	王端宜, 吴文亮, 张肖宁, 等. 基于数字图像处理和有限元建模方法的沥青混合料劈裂试验数值模拟[J]. 吉林大学学报(工学版), 2011, 41(4): 968-973. WANG Duanyi, WU Wenliang, ZHANG Xiaoning, et al. Numerical simulation of splitting test of asphalt mixture based on DIP-FEM[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(4): 968-973. (in Chinese) [本文引用:1]
[6]	石立万, 王端宜, 徐驰, 等. 基于离散元法的沥青混合料骨架细观性能研究[J]. 华南理工大学学报(自然科学版), 2015, 43(10): 50-56. SHI Liwan, WANG Duanyi, XU Chi, et al. Investigation into meso performance of asphalt mixture skeleton based on discrete element method[J]. Journal of South China University of Technology (Natural Science Edition), 2015, 43(10): 50-56. (in Chinese) [本文引用:1]
[7]	石福周, 常明丰, 裴建中, 等. 基于离散元方法的沥青混合料矢量场细观分析[J]. 长安大学学报(自然科学版), 2014, 34(2): 9-15. SHI Fuzhou, CHANG Mingfeng, PEI Jianzhong, et al. Mesoscopic analysis on vector field of asphalt mixture using discrete element method[J]. Journal of Chang'an University (Natural Science Edition), 2014, 34(2): 9-15. (in Chinese) [本文引用:1]
[8]	吕慧杰, 刘涵奇, 罗蓉. 基于单轴压缩蠕变试验求解沥青混合料松弛模量[J]. 武汉理工大学学报(交通科学与工程版), 2016, 40(6): 1067-1072. LYU Huijie, LIU Hanqi, LUO Rong. Determination of relaxation modulus of asphalt mixtures using uniaxial compressive creep test[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2016, 40(6): 1067-1072. (in Chinese) [本文引用:1]
[9]	周博, 汪华斌, 赵文锋, 等. 黏性材料细观与宏观力学参数相关性研究[J]. 岩土力学, 2012, 33(10): 3171-3178. ZHOU Bo, WANG Huabin, ZHAO Wenfeng, et al. Analysis of relationship between particle mesoscopic and macroscopic mechanical parameters of cohesive materials[J]. Rock and Soil Mechanics, 2012, 33(10): 3171-3178. (in Chinese) [本文引用:1]
[10]	杨盼盼, 肖鹏, 丁燕, 等. 基于离散元法的沥青混合料细观特性分析[J]. 中国矿业大学学报, 2018, 47(4): 900-906. YANG Panpan, XIAO Peng, DING Yan, et al. Microstructure characteristics analysis of asphalt mixture based on the discrete element method[J]. Journal of China University of Mining & Technology, 2018, 47(4): 900-906. (in Chinese) [本文引用:1]
[11]	高虎, 杨新华, 唐鹏. 沥青混合料车辙变形的离散元数值模拟[J]. 固体力学学报, 2018, 39(3): 277-283. GAO Hu, YANG Xinhua, TANG Peng. Discrete element numerical simulation on rutting deformation of asphalt mixture[J]. Chinese Journal of Solid Mechanics, 2018, 39(3): 277-283. (in Chinese) [本文引用:1]
[12]	高虎, 杨新华, 陈龙. 沥青混合料半圆弯曲断裂实验和离散元数值分析[J]. 土木工程与管理学报, 2018, 35(4): 123-129. GAO Hu, YANG Xinhua, CHEN Long. Experimental and discrete element analysis of semi-circular bending fracture of heterogeneous asphalt mixture[J]. Journal of Civil Engineering and Management, 2018, 35(4): 123-129. (in Chinese) [本文引用:1]
[13]	陈渊召, 李振霞. 基于离散元法的橡胶颗粒沥青混合料细观结构分析[J]. 哈尔滨工业大学学报, 2013, 45(4): 116-121. CHEN Yuanzhao, LI Zhenxia. Meso-structure of crumb rubber asphalt mixture based on discrete element method[J]. Journal of Harbin Institute of Technology, 2013, 45(4): 116-121. (in Chinese) [本文引用:1]
[14]	刘卫东, 高英, 黄晓明, 等. 沥青路面现场压实细观特性分析[J]. 哈尔滨工业大学学报, 2019, 51(3): 99-106. LIU Weidong, GAO Ying, HUANG Xiaoming, et al. Mesoscopic characteristics of asphalt pavement during field compaction[J]. Journal of Harbin Institute of Technology, 2019, 51(3): 99-106. (in Chinese) [本文引用:1]
[15]	李友云, 胡迪, 胡白石, 等. 沥青混合料细观力学数值分析[J]. 北方交通, 2015(4): 59-64. LI Youyun, HU Di, HU Baishi, et al. The multi-scale numerical analysis of asphalt pavement[J]. Northern Communications, 2015(4): 59-64. (in Chinese) [本文引用:1]
[16]	中华人民共和国交通运输部. 公路路基设计规范: JTG D30—2015[S]. 北京: 人民交通出版社, 2015. Ministry of Transport of the People’s Republic of China. Code for design of highway subgrade: JTG D30—2015[S]. Beijing: People’s Communications Press, 2015. (in Chinese) [本文引用:1]
[17]	中华人民共和国国家标准局. 车辆振动输入-路面不平度表示方法: GB/T 7031—1986[S]. 北京: 人民交通出版社, 1986. National Bureau of Stand ards of the People’s Republic of China. Vehicle vibration—Describing method for road surface irregularity: GB/T 7031—1986[S]. Beijing: People’s Communications Press, 1986. (in Chinese) [本文引用:1]
[18]	Itasca Consulting Group. PFC2D users’ manual (version 3. 1)[M]. Minnesota: Itasca Consulting Group Inc, 2004. [本文引用:1]
[19]	陈俊, 张东, 黄晓明. 离散元颗粒流软件(PFC)在道路工程中的应用[M]. 北京: 人民交通出版社, 2015: 229-238. CHEN Jun, ZHANG Dong, HUANG Xiaoming. Application of discrete element particle flow software (PFC) in road engineering[M]. Beijing: People's Communications Press, 2015: 229-238. (in Chinese) [本文引用:1]
[20]	刘登普, 龙劭. 行车荷载下沥青路面响应分析[J]. 公路与汽运, 2006(3): 55-57. LIU Dengpu, LONG Shao. Response analysis of asphalt pavement under driving load[J]. Highways &Automotive Applications, 2006(3): 55-57. (in Chinese) [本文引用:1]

2009

0.0

... 目前,很多学者从细观角度对沥青路面进行分析逐渐成为研究方向之一^[1,2] ...

2011

0.0

... 目前,很多学者从细观角度对沥青路面进行分析逐渐成为研究方向之一^[1,2] ...

2015

0.0

... 国内外专家学者针对于沥青混合料细观力学进行了一系列研究,文献[3]模拟了单轴压缩试验,结果表明,随轴向应变的增加,颗粒之间的接触压力个数逐渐减小,接触拉力个数逐渐增大,且颗粒之间的接触力均值先增加后减小 ...

2010

0.0

陈俊, 黄晓明. 基于离散元法的沥青混合料虚拟疲劳试验方法[J]. 吉林大学学报(工学版), 2010, 40(2): 435-440.

CHEN

Jun

, HUANG

Xiaoming

. Virtual fatigue test of asphalt mixture based on discrete element method[J]. Journal of Jilin University (Engineering and Technology Edition), 2010, 40(2): 435-440. (in Chinese)

Virtual fatigue tests of the small beam specimen from asphalt mixture(AM) were performed using the discrete element method(DEM) to investigate the fatigue mechanism of AM microscopically. A gradation derivation formula was established by the probability theory to convert the volumetric aggregate gradation into the twodimensional(2D) digital speciment quantity gradation. Taking the irregular form of the aggregate into account, a generation program of the virtual structure of the 2D digital specimen was compiled based on MonteCarlo method and the specimens were generated. A whole package of virtual fatigue test methods of AM, including the establishment of DEM model of AM, the selection of the contact modes of the discrete elements, and the criteria judging the fatigue failure, was established based on DEM. The fatigue tests of the small beam from AM were performed, and their results were compared with those of its virtual fatigue tests based on DEM. Their good agreement implicated that the proposed virtual 2D beam fatigue test based on DEM can predict well the fatigue life of AM. The virtual beam fatigue test can be used as an auxiliary means to evaluate the fatigue performance of AM.

School of Transportation, Southeast University, Nanjing 210096,China

为了从细观角度深入分析沥青混合料疲劳机理，运用离散元方法实现了沥青混合料小梁试件的虚拟疲劳试验。首先，根据概率理论，建立了由混合料三维体积级配至沥青混合料二维数字试件数量级配推导公式；接着，根据蒙特卡洛方法，编制了考虑集料不规则形状的沥青混合料二维数字试件生成程序，以此生成了沥青混合料二维数字试件；然后，结合离散元基本原理，提出了包括沥青混合料离散元模型的建立、离散单元的接触模式选择和疲劳失效判断标准在内的一整套沥青混合料虚拟疲劳试验方法；最后，进行了沥青混合料小梁疲劳试验，并与基于离散元方法的虚拟试验结果进行了比较分析。研究结果表明，虚拟试验结果与真实试验结果相差无几，所建立的虚拟疲劳试验方法可以作为沥青混合料疲劳性能分析的辅助手段。

... 文献[4]通过实验获取模型细观参数,建立了沥青混合料小梁实验模型,将虚拟实验结果与室内实验对比,其结果基本一致,表明离散元法虚拟疲劳试验方法可以作为沥青混合料疲劳性能分析的辅助手段 ...

2011

0.0

王端宜, 吴文亮, 张肖宁, 等. 基于数字图像处理和有限元建模方法的沥青混合料劈裂试验数值模拟[J]. 吉林大学学报(工学版), 2011, 41(4): 968-973.

WANG

Duanyi

, WU

Wenliang

, ZHANG

Xiaoning

, et al. Numerical simulation of splitting test of asphalt mixture based on DIP-FEM[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(4): 968-973. (in Chinese)

A finite element analysis model was built for the asphalt mixture including the aggregate, the air void, and the asphalt mastic using the specimen images acquired by industrial CT and the digital image processing(DIP) as well as the finite element modeling(FEM) technique. The splitting tests(indirect tensile tests) of the asphalt mixture were simulated in consideration of the air void distribution, different loading directions, and different aggregate asphalt modulus ratios. The results indicate that the stress concentration factor can be used to describe the distribution of stress inside the asphalt mixture, and the mixture gradation, the modulus ratio, the air void and the loading position affect the simulation results significantly. By the DIP-FEM method the microstructure and the macromechanics of the asphalt mixture can be interrelated well.

School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, China

应用数字图像处理技术及工业CT扫描获得试件图像，结合有限元建模方法，建立了包含集料、空隙和胶浆在内的沥青混合料有限元模型，并模拟研究了沥青混合料劈裂试验。结果表明：通过定义应力集中因子，可用来描述沥青混合料内部应力的不均匀分布，级配类型、模量比、有无空隙及加载位置都对模拟结果有较大影响。采用DIP-FEM方法能够很好地将沥青混合料的微观结构和宏观力学性能结合起来。

... 文献[5]基于离散元方法进行了沥青混合料劈裂试验模拟,表明采用DIP-FEM方法能将沥青混合料的微观结构和宏观力学性能结合起来 ...

2015

0.0

... 文献[6]通过建立上面层沥青路面模型,分析了沥青混合料骨架特性,骨架承受加载力的70%~80%,对应力传递的贡献率达70%以上 ...

2014

0.0

... 文献[7]利用离散元法建立沥青混合料试件,研究了集料及砂浆随时间的变化情况,并于实测值进行对比验证,其结果基本一致,表明该方法具有一定可行性 ...

2016

0.0

... 文献[8]对黏弹性状态的沥青混合料进行单轴压缩实验,通过测得蠕变柔量计算沥青混合料松弛模量,用于预测沥青路面的黏弹性响应 ...

2012

0.0

... 文献[9]通过离散元法对黏性土类材料进行了平面双轴压缩试验模拟 ...

2018

0.0

... 文献[10]建立了双层车辙试件模型,分析了试件内部接触力变化及颗粒空间运动轨迹,结果表明,上面层主要受压,拉应力则主要分布在下面层,SMA-13骨架性能比AC-20好 ...

2018

0.0

... 文献[11]采用Burgers本构关系开展了车辙变形细观模拟,研究了骨料分布、荷载、温度等对车辙深度的影响,结果表明,当超载和高温共同作用时,车辙变形会大幅度增加 ...

2018

0.0

... 文献[12]研究分析了沥青混合料半圆弯曲断裂的开裂机理,发现法向和切向接触力在裂缝产生中都具有显著作用 ...

2013

0.0

陈渊召, 李振霞. 基于离散元法的橡胶颗粒沥青混合料细观结构分析[J]. 哈尔滨工业大学学报, 2013, 45(4): 116-121.

CHEN

Yuanzhao

, LI

Zhenxia

. Meso-structure of crumb rubber asphalt mixture based on discrete element method[J]. Journal of Harbin Institute of Technology, 2013, 45(4): 116-121. (in Chinese)

To analyze failure mechanism and internal essence of macro-mechanical properties difference for crumb rubber asphalt micture, discrete element models are established, contact force vector diagram, force chain network chart and contact force local enlarging graphs belong to gap gradation crumb rubber asphalt mixture, continuous grading crumb rubber asphalt mixture and asphalt mixture are systematically studied firstly, their internal strength chain, weak force chain and deformation characteristics are obtained respectively, their bearing capacity sorting and deformability sorting are proposed. Then, local enlarged drawing in adhesive contact failure position and displacement vector map of crumb rubber asphalt mixture are deeply researched, failure mechanism of crumb rubber asphalt mixture is obtained. The results show that their bearing capacity from big to small in proper order is asphalt mixture, gap gradation crumb rubber asphalt mixture, continuous grading crumb rubber asphalt mixture. Their deformability from big to small in proper order is asphalt mixture, gap gradation crumb rubber asphalt mixture, continuous grading crumb rubber asphalt mixture.

为分析橡胶颗粒沥青混合料的破坏机理及宏观力学性能差异的内在本质,建立离散元模型,首先系统研究间断级配橡胶颗粒沥青混合料、连续级配橡胶颗粒沥青混合料和普通沥青混合料的接触力矢量图、力链网络图及接触力局部放大图,分别得到其内部的强力链、弱力链和变形特点,提出了其承载能力排序和变形能力排序;然后深入研究橡胶颗粒沥青混合料的位移矢量图和黏结接触破坏位置局部放大图,得到橡胶颗粒沥青混合料的破坏机理．结果表明,承载能力由大到小依次为:普通沥青混合料、间断级配橡胶颗粒沥青混合料、连续级配橡胶颗粒沥青混合料;变形能力由小到大依次为:普通沥青混合料、间断级配橡胶颗粒沥青混合料、连续级配橡胶颗粒沥青混合料．

... 文献[13]对混凝土的热膨胀系数性能进行了研究,证实了细观力学方法的有效性 ...

2019

0.0

... 文献[14]利用PFC3D进行了沥青混合料的离析及级配模拟,证明了通过离散元法进行沥青路面压实模拟探究细观行为是合理可行的 ...

2015

0.0

... 文献[15]通过对比路面细观数值模型与均质模型,验证了细观状态下分析路面受力情况的有效性 ...

2015

0.0

... 地基层无限延伸,其中路床主要用于承受及分散车辆荷载,JTG D30—2015《公路路基设计规范》^[16]中规定路床深度80 cm,80 cm以外的地基深度对沥青路面力学响应影响较小,同时为减小计算工作量,本文地基层采用厚度为80 cm ...

1986

0.0

... 本文采用GB/T 7031—86《车辆振动输入—路面不平度表示方法》^[17]中路面功率谱密度为 ...

2004

0.0

... 其中,文献[18]通过试错法拟合标准单轴压缩试验从而获取细观参数,本文也采用此方法,沥青混合料单轴压缩应力-应变模拟试验与标准试验对比见图5,其应力-应变曲线总体趋势相似,此时模型参数作为相应结构层细观参数 ...

2015

0.0

... 根据文献[19],将车辆轮胎简化为加载板进行加载,假设轮胎接地面积为正方形,长度为21 ...

2006

0.0

刘登普, 龙劭. 行车荷载下沥青路面响应分析[J]. 公路与汽运, 2006(3): 55-57.

LIU

Dengpu

, LONG

Shao

. Response analysis of asphalt pavement under driving load[J]. Highways &Automotive Applications, 2006(3): 55-57. (in Chinese)

利用大型通用有限元软件ANSYS,将行车荷载简化为移动的均布荷载,对沥青路面表面弯沉、层底变拉应力、路面层内部压应力及剪应力等进行了计算分析,得出了它们随时间变化的规律.

... 由于缺乏离散元模型试验数据证明,依据文献[20],采用有限元软件建立二维路面模型,其中,在有限元模型中已经采用试验方法证明 ...