基于神经网络的时变无线信道仿真

引用本文

刘留, 李慧婷, 张嘉驰, 李一倩, 周涛. 基于神经网络的时变无线信道仿真[J]. 北京交通大学学报, 2020,44(2): 74-82.
LIU Liu, LI Huiting, ZHANG Jiachi, LI Yiqian, ZHOU Tao. Wireless channel simulation based on neural network[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2020,44(2): 74-82.
Doi:10.11860/j.issn.1673-0291.20190099 复制到剪切板

Permissions

北京交通大学学报编辑部所有

基于神经网络的时变无线信道仿真

刘留^1,², 李慧婷¹, 张嘉驰¹, 李一倩¹, 周涛¹

1.北京交通大学电子信息工程学院,北京 100044

2.中国科学院计算技术研究所移动计算与新型终端北京市重点实验室,北京 100190

第一作者:刘留(1981—),男,云南昆明人,教授,博士,博士生导师.研究方向为无线信道测量与建模和时变信道通信信号处理.email:liuliu@bjtu.edu.cn.

收稿日期: 2019-08-29

基金: 北京市自然科学基金(L172030)

摘要

提高频谱利用率、实现超大容量传输的前提是精准掌握无线信道特性信息.研究了反馈神经网络(Back Propagation Neural Network, BPNN)在无线信道多普勒功率谱仿真中的应用.利用大量样本训练BPNN实现对时变信道进行预测.仿真结果表明,与传统方法对比,BPNN的仿真效果更接近理论值,误差更小,具备很好的容错性,同时模型输出结果的频域呈U型谱,时域自相关函数满足第一类贝塞尔函数,很好地符合Jakes模型的时频域条件.对3种方法的时间复杂度进行比较,结果表明BPNN的时间复杂度最高,牺牲了时间复杂度但换取了高精度和低误差.对3种误差逆向传播算法的仿真结果进行对比,发现列文伯格-马夸尔特( Levenberg-Marquardt, L-M)算法训练BPNN的均方误差最低,效果最佳.

关键词: 无线通信; 反馈神经网络; 多普勒效应; 时变信道; 正弦波叠加法; 成型滤波法

中图分类号:U285 文献标志码:A 文章编号:1673-0291(2020)02-0074-09

Wireless channel simulation based on neural network

LIU Liu^1,², LI Huiting¹, ZHANG Jiachi¹, LI Yiqian¹, ZHOU Tao¹

1. School of Electronic and Information Engineering, Beijing Jiaotong University, Beijing 100044, China

2. Beijing Key Laboratory of Mobile Computing and New Terminal, Chinese Academy of Sciences, Beijing 100190, China

Fund:Beijing Natural Science Foundation(L172030)

Abstract

In order to improve the spectrum utilization rate and realize ultra-large capacity transmission, the premise is to accurately grasp the wireless channel characteristic information.This paper studies the application of Back Propagation Neural Network (BPNN) in Doppler power spectrum simulation of wireless channel. BPNN is trained by using a large number of samples to predict time-varying channels. The simulation results show that compared with traditional methods, BPNN simulation results are closer to theoretical values, with less errors and good fault tolerance. At the same time, the frequency domain of the model output results is U-shaped spectrum, and the time domain autocorrelation function satisfies the first type of Bessel function, which is in good accordance with the time-frequency domain conditions of Jakes model.The time complexity of the three methods is compared. The results show that BPNN has the highest time complexity, sacrificing the time complexity but obtaining high precision and low error. Besides, the simulation results of three error back propagation algorithms are compared. It is found that Levenberg-Marquardt algorithm has the lowest mean square error and the best effect in training BPNN.

Keyword: wireless communication; back propagationneural network; Doppler effect; time-varying channel; sine wave superposition method; shaping filtering method

文章图片

无线信道作为信号传输的媒介, 其性能的好坏直接决定着通信的质量.为在有限的频谱资源上尽可能地高质量、大容量传输有用信息, 就要求设计者必须清楚地了解信道的特性, 掌握电波在信道中的传播及变化规律, 即建立精准的信道模型^[1].

信号在信道中传输会产生衰落, 衰落又通常分为大尺度衰落和小尺度衰落.大尺度衰落表征了接收信号在一定时间内的均值随传播距离和环境的变化呈现的缓慢变化, 了解其特征主要用以分析信道的可用性、选择载波频率、切换及网络规划, 其规律相对简单, 已有很多成熟的模型.而小尺度衰落表征了接收信号短距离(几个波长)或短时间内的快速波动, 是移动信道的主要特征, 其中Clarke信道模型描述的小尺度平坦衰落信道中, 移动台接收信号具有基于散射方式的场强统计特性, 这正符合市区移动通信环境不存在直射路径的特点, 其包络统计特性服从瑞利分布, 因此又称为瑞利衰落信道模型^[2].然而Clarke参考模型是一种理想模型, 物理不可实现, 实际应用中通过正弦波叠加法和成型滤波法两种来实现时变信道仿真.但上述两种传统方法存在着种种缺陷, 如:正弦波叠加法的精度较低, 而成型滤波法的计算量较大, 不适宜用于大数据量的信道仿真^[3].

随着人工智能的发展, 机器学习和无线通信的结合也吸引了众多学者的关注.已有相关工作研究了机器学习, 尤其是神经网络在无线传输层中的应用.文献[4]基于神经网络对多径信道的输入输出响应进行了建模, 讨论了建模的方法并给出了仿真的结果.文献[5]基于多层前向神经网络研究了时变信道建模方法, 仿真结果表明前向神经网络可以很好地跟踪非稳态时变信道的特性.文献[6]基于深度学习搭建了深度MIMO(Multiple-Input Multiple-Output)检测器, 将梯度投影法的迭代过程展开成深度神经网络, 折中了算法的检测性能、复杂度与收敛性.然而这些研究的重点主要着眼于应用机器学习的方法解决无线信道建模的问题, 并没有对利用神经网络仿真时变信道中多普勒效应的问题进行深入研究.神经网络作为一种非线性统计性数据建模工具, 具有极强的学习能力, 能在复杂情况下逼近非线性系统, 具有很好的容错性和鲁棒性.利用神经网络学习预测时变信道模型, 可以降低数据计算量, 而且拥有高精度和强灵活性^[7].

本文作者研究了反馈神经网络(Back Propagation Neural Network, BPNN)在无线信道多普勒功率谱仿真中的应用, 利用传统的正弦波叠加法和成型滤波法产生的大量多普勒功率谱训练样本数据, 通过训练BPNN实现对时变信道进行预测, 将仿真结果进行了对比分析.并对3种方法的时间复杂度进行了讨论.此外, 还对3种常见的误差逆向传播算法的预测效果进行了比较.

1 传统时变信道及其生成方法

信号在移动信道中传输, 由于受到衰落和噪声的影响, 导致信号强度、频率等发生相应变化.

小尺度平坦衰落信道中^[8], 由于周边散射物的影响, 导致接收端接收到的是来自不同路径的多径信号.同时, 移动的移动台将会导致每条多径分量具有不同的多普勒频移.假设移动台接收的信号的入射角度 $α$ 在 $[0, 2 π]$ 间均匀分布, 这样就得到了具有特定环境下的多普勒功率谱.通常在具有瑞利衰落的环境下, 多普勒功率谱用以描述接收信号功率随多普勒频率的变化, 具有Jakes功率谱密度函数, 即U型谱的特性, 其表达式^[9]为

$S (f) = \frac{E_{0}}{π f_{m} \sqrt[]{1 - (f / f_{m})^{2}}}, |f| \leq f_{m}$ (1)

式中: $f_{m}$ 为最大多普勒频移; $E_{0} = \overset{N - 1}{\sum_{i = 0}} {|a_{i}|}^{2}$ 为增益, $a_{i}$ 为第 $i$ 径上的复增益因子.

接收信号的自相关函数为

$\begin{matrix} R (τ) = E_{0} \int_{0}^{2π} \frac{1}{2 π} \exp (j 2 π f_{m} \cos ατ) d α = E_{0} J_{0} (2 π f_{d} τ) \end{matrix}$ (2)

式中: $τ$ 为时间延迟; $f_{d}$ 为多普勒频移; $J_{0}$ 为第1类0阶贝塞尔函数, 说明信号的自相关函数符合第1类贝塞尔函数 $J_{0} (x)$ 包络与按 $1 / \sqrt[]{x}$ 速率衰减的正弦或余弦函数类似的特性.许多信道建模和仿真方法的研究, 均以Clarke信道模型的统计特性作为性能评估的标准, 但Clarke参考模型是一种理想模型, 由大量正弦波相加(理想统计特性在正弦波的数量 $N$ 为无穷大时取得), 物理上不可实现.

1.1 正弦波叠加法

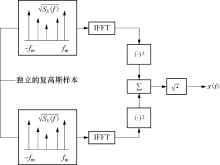
正弦波叠加法是利用确定性过程来模拟随机过程.根据概率论和瑞利分布的定义, 多个不同频率的正弦波叠加, 其幅度服从高斯分布.当实部和虚部均用多个不同频率的正弦波叠加, 则实部、虚部均分别服从高斯分布.而两个高斯变量的平方和的根服从瑞利分布, 因此包络服从瑞利分布^[10].正弦波叠加法易于实现、占用计算资源少, 但是产生的多普勒功率谱是由多个离散频率点上的冲激构成, 并且自相关性能不够理想, 因而实际应用中常采用的是基于正弦叠加法的Jakes仿真模型^[11], 其框图见图1.其中 $f_{c}$ 为中心频率.

	Figure Option View Download New Window
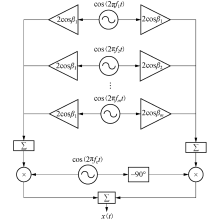	图1 Jakes正弦波叠加法仿真模型实现框图Fig.1 Jakes sinusoidal superposition method simulation model implementation block diagram

图1的左右两支路都由多个不同频率的正弦波叠加, 其中:

$f_{n} = \{\begin{array}{l} f_{m} \cos \frac{n}{4 M + 2}, n = 1, 2, \dots, M - 1 \\ f_{m}, n = M \end{array}$ (3)

$β_{n} = \{\begin{array}{l} \frac{π n}{M}, n = 1, 2, \dots, M - 1 \\ \frac{π}{4}, n = M \end{array}$ (4)

式中: $M$ 为正弦波发生器数目.左右支路的输出分别代表信号的实部和虚部, 最后相加得到的信号包络则满足瑞利分布.

1.2 成型滤波法

成型滤波法的仿真结构如图2所示, 它是将高斯白噪声输入成型滤波器来产生指定形状的多普勒功率谱, 其中 $\sqrt[]{S_{E} (f)}$ 为幅值.实部和虚部均是具有特定形状多普勒功率谱的高斯有色噪声, 因此包络服从瑞利分布^[12].利用Matlab仿真基于正弦波叠加法和成型滤波法得到的功率谱和时域自相关函数如图3所示, 可以看到基于这两种方法得到的功率谱均符合多普勒功率谱的特性, 呈U型谱, 由成型滤波法得到的功率谱曲线在曲线中部起伏较小, 且曲线更贴近U型谱.

	Figure Option View Download New Window
	图2 成型滤波法仿真模型实现框图Fig.2 Blocking filter simulation model implementation block diagram

	Figure Option View Download New Window
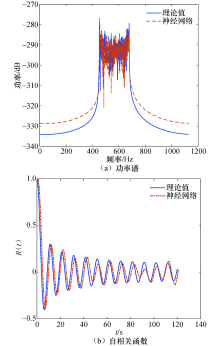
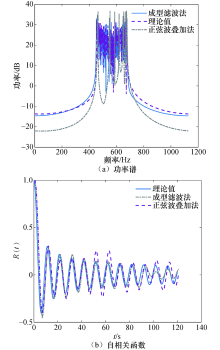	图3 基于两种方法得到的功率谱和自相关函数Fig.3 Based on the power spectrum and autocorrelation functions obtained by the two methods

自相关函数也都基本符合第1类贝塞尔函数, 由正弦波叠加法得到的曲线的中部和尾部起伏较大, 并不总是符合衰减特性, 由此可说明成型滤波法的误差小于正弦波叠加法.成型滤波法采用的是随机噪声, 因而随机性等各方面性能都比正弦叠加法更为理想.由于通常情况下通信系统的采样速率非常高, 最大多普勒频率与采样率相比很小, 因此成型滤波器需要的带宽很小, 直接实现非常困难.

2 神经网络建模时变信道

2.1 利用神经网络仿真时变衰落信道

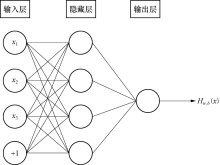
通信信道可以看作一个非线性的复杂系统.当对一个非线性系统采用神经网络进行建模时, 假设x表示系统的 $N_{x}$ 维输入信号, y代表系统的 $N_{y}$ 维输出信号.y和x之间的映射关系可能是高度非线性和多维的, 输入输出关系的数值模型会随着场景及影响因素的变化而发生改变, 难以确定准确的模型^[13].而利用神经网络对信道模型进行预测, 该模型能够学习非线性系统的输入输出数据, 进而逼近系统的输入输出关系.通常, 这种输入输出关系的数值模型定义为: $y = f (x, ω, b)$ , 其中ω 是一个 $N_{ω}$ 维矢量, 代表神经网络模型内的权重, b是一个 $N_{b}$ 维矢量, 代表神经网络模型内的阈值.经过代表f的x-y关系的训练数据对学习训练后, 神经网络模型能代表具体的一个系统的输入输出关系.其中x-y训练数据对, 其可以通过测量得到, 也可以通过精确地仿真得到^[14].

根据Kolmogorov定理^[15], 3层网络经过充分学习后能几乎逼近任何函数, 所以建立如图4所示的3层结构的神经网络进行学习训练.神经网络的核心思想中经过不断地训练, 找到一个合适的参数拟合输入输出的映射关系.理论上, 神经网络可以拟合任意线性或者非线性的函数.

	Figure Option View Download New Window
	图4 三层神经网络结构图Fig.4 Structure diagram of three-layer neural network

2.2 BPNN原理

采用BPNN对信道模型进行预测, 训练模型逼近时变信道的输入输出关系.BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络, 误差反向传播算法就是寻找合适 $ω, b$ 的一种思路^[16].利用误差反向传输来寻找误差的来源, 然后根据梯度下降的原理更新 $ω, b$ .

1)将信道参数进行归一化预处理.

首先, 利用传统的正弦波叠加法和成型滤波法产生的大量多普勒功率谱样本数据作为输入信号, 再利用BPNN进行训练之前需要将输入数据进行归一化预处理, 采用min-max标准化方法, 即可将原始数据的取值范围映射到 $[0, 1]$ 区间.

$x = \frac{x - x_{\min}}{x_{\max} - x_{\min}}$ (5)

然后将归一化后的样本数据按输入层→ 隐含层→ 输出层的方向传递, 经过非线性变换, 产生输出信号.当各层神经元的激活函数均采用sigmod函数, 表达为^[17]

$f (x) = \frac{1}{1 + e^{- (W^{T} x + b)}}$ (6)

式中: $W = [w_{ji}^{(p)}]$ 表示网络权值矩阵; $w_{ji}^{(p)}$ 表示第 $p - 1$ 层中第 $i$ 个神经元与第 $p$ 层中第 $j$ 个神经元的连接权重; $x$ 表示输入向量; $b = [b_{j}^{(p)}]$ ; $b_{j}^{(p)}$ 表示第 $p$ 层中第 $j$ 个神经元的阈值.

更新公式如下

$W (t + 1) = W (t) - η \frac{\partial E (t)}{\partial W (t)}$ (7)

$b (t + 1) = b (t) - η \frac{\partial E (t)}{\partial b (t)}$ (8)

式中: $E (t)$ 表示总误差函数; $t$ 表示训练次数; $η \in (0, 1)$ 表示步长因子.

2)信号正向传输, 计算网络总误差 $E (t) .$

3)将实际输出与期望输出相比较, 如果不相符, 计算 $E (t)$ 并转入误差的反向传输过程.将输出误差按输出层→ 隐含层→ 输入层的方向反向传递, 并将误差分摊给各层的所有单元, 计算每个节点的残差为

$\frac{\partial E (t)}{\partial w_{ji}^{(p)}} = x_{ji}^{(p)} δ_{j}^{(p)}$ (9)

$\frac{\partial E}{\partial b_{j}^{(p)}} = δ_{j}^{(p)}$ (10)

$δ_{j}^{(p)} = f^{'} \cdot \sum_{k} w_{jk}^{(p + 1)} δ_{k}^{(p + 1)}$ (11)

式中: $δ_{j}^{(p)}$ 称为第 $p$ 层第 $j$ 个神经元的误差项; $f$ 表示当前神经元的输出, 对于输出层的神经元其误差项为

$δ_{k} = f' (x_{k}) \cdot [t_{k} - f (x_{k})]$ (12)

4)将从各层获得的误差信号作为调整各单元的权值的依据, 使用残差来更新权值 $ω$ 及阈值 $b$ , 使误差沿梯度方向下降.

5)反复上述学习训练过程, 直至求得的误差小于设定阈值或者达到诸如训练次数等迭代训练要求.确定与最小误差相对应的网络参数(权值和阈值), 训练停止^[18].

常见的误差逆向传播算法是梯度下降法, 它是使用最广泛的最小二乘最优化算法^[19].梯度下降法以负梯度方向作为极小化算法的下降方向, 是无约束优化中最简单的方法, 它具有储存量小、结构简单、易于实现等优点, 但其缺点在于:在远离鞍点的地方下降很快, 而在靠近鞍点的地方下降很慢, 且损失函数可能收敛到鞍点^[20].

另一种使用广泛的方法是高斯牛顿法, 它是一种非线性最小二乘最优化方法.其利用了目标函数的泰勒展开式把非线性函数的最小二乘化问题化为每次迭代的线性函数的最小二乘化问题.高斯牛顿法的缺点在于:若初始点距离极小值点过远, 迭代步长过大会导致迭代下一代的函数值不一定小于上一代的函数值^[21].

鉴于梯度下降法和高斯牛顿法的缺点, 本文采用的误差逆向传播算法是列文伯格-马夸尔特(Levenberg-Marquardt, L-M)算法.在L-M算法中, 每次迭代是寻找一个合适的阻尼因子 $λ$ , 当 $λ$ 很小时, 算法就变成了高斯牛顿法的最优步长计算式, $λ$ 很大时, 蜕化为梯度下降法的最优步长计算式, 因此L-M算法介于牛顿法与梯度下降法之间, 对于过参数化问题不敏感, 能有效处理冗余参数问题, 使代价函数陷入局部极小值的机会大大减小, 这些特性使得L-M算法在图像识别等领域得到广泛应用^[22].但L-M算法也存在一些缺点:

1)L-M算法需要对每一个待估参数求偏导, 因此当拟合函数 $f$ 非常复杂, 或者待估参数相当地多, 那么可能不适合使用L-M算法.

2)对于非常大的数据集和神经网络, L-M算法的Jacobian矩阵会变得很大, 需要的内存也较大.因此L-M算法不太适合应用于大数据集的情况.

3 仿真与验证结果分析

3.1 利用BPNN进行训练预测和仿真

利用Matlab进行BPNN训练, 仿真参数设置为:每层节点数为100, 隐含层层数为1, 训练次数为1 000, 设定误差为0.1, 训练集为70%, 测试集/验证集为15%, 输入层神经元数为100, 隐含层神经元数为80, 输出层神经元数为100.神经网络对于隐含层层数的要求是大于等于1, 而隐含层数量过高时, 准确率可能反而会下降, 这是因为反向传播算法中的梯度经过越多的隐含层就会越小, 并逐渐趋近于零, 这种现象称为梯度消失或梯度弥散.因此层数越多越容易发生过拟合, 均方误差可能增大, 故设置隐含层数为1.另外通过误差与节点数的测试, 选择误差最小时的节点数80.首先通过正弦叠加法和成型滤波法得到大量多普勒功率谱训练样本数据, 用来训练神经网络, 其中训练集占70%、测试集和验证集各占15%.

由神经网络学习预测得到的结果见图5.

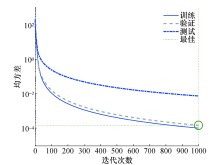
	Figure Option View Download New Window
	图5 神经网络预测效果Fig.5 Neural network prediction effect

可以看到神经网络预测值的频域符合U型谱, 时域的自相关函数符合第1类贝塞尔函数, 因此神经网络预测值符合Jakes模型.神经网络训练1 000 次后的均方误差效果如图6所示, 可以看到均方误差随着训练次数的增加而下降, 圆圈表明训练得到最小均方误差的时间, 即在训练第999次时均方误差达到最小值1.43× 10^-4, 说明BP神经网络模型预测精度很高.

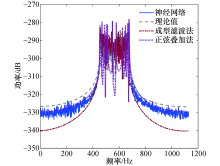
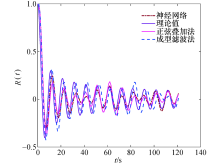
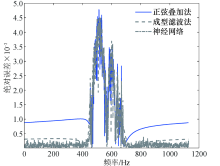
	Figure Option View Download New Window
	图6 迭代次数与均方误差关系Fig.6 Relationship between iteration times and mean square error

随后, 将神经网络预测值与正弦波叠加法、成型滤波法以及理论值比较, 多普勒功率谱对比效果如图7所示, 可以看到神经网络预测得到的多普勒功率谱更接近理论值, 而正弦波叠加法和成型滤波法得到的多普勒功率谱虽也符合U型谱的特征, 但与理论值存在较大的差异.自相关函数对比如图8所示, 可以看到神经网络预测得到的自相关函数更接近理论的第1类贝塞尔函数, 而由正弦波叠加法和成型滤波法得到的自相关函数, 在曲线的中部和尾部起伏较大, 并不总是符合第1类贝塞尔函数的衰减特征, 因此由神经网络预测的拟合程度更高.神经网络预测、正弦波叠加法及成型滤波法三者与理论值的绝对误差对比如图9所示, 可以看到神经网络预测的误差更接近于0, 其次是成型滤波法和正弦波叠加法, 说明神经网络预测的误差低于传统的两种方法.由此可见, 利用神经网络对时变信道仿真建模比传统方法的精度更高.

	Figure Option View Download New Window
	图7 功率谱对比Fig.7 Power spectrum comparisons

	Figure Option View Download New Window
	图8 自相关函数对比Fig.8 Autocorrelation function comparisons

	Figure Option View Download New Window
	图9 绝对误差对比Fig.9 Absolute error comparison

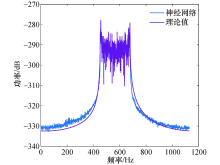
神经网络对被建模的输入输出数据对进行充分学习, 训练好的网络模型可对实际数据进行仿真.神经网络仿真数据与理论值进行比较, 如图10所示, 可以看到拟合程度非常高, 说明训练好的网络模型精度极高, 能较好地预测U型谱.

	Figure Option View Download New Window
	图10 神经网络仿真数据Fig.10 Neural network simulation data

3.2 不同方法的时间复杂度对比

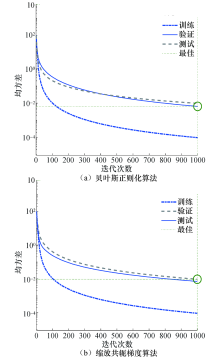
正弦波叠加法对Clarke理论模型进行了简化, 仿真所需的低频振荡器(即正弦波发生器)数目由 $N$ 减少为 $\frac{(N / 2 - 1)}{2}$ , 仿真效率大大提高, 其计算复杂度为 $O (n)$ , 其中 $n$ 为序列点数.成型滤波法的实现需要涉及快速傅里叶逆变换 (Inverse Fast Fourier Transformation, IFFT), 其计算复杂度为 $O (n \ln n)$ , 其中 $n$ 为序列点数.BPNN经由误差逆向传播算法训练, 过程包括信号的正向传输及误差的反向传输, 其时间复杂度为 $O (n^{3})$ , 其中 $n$ 为网络节点数^[23].由于此3层神经网络的输入层和输出层节点数为序列点数, 隐含层节点数是通过误差与节点数的测试后人为设定的, 因此网络节点数大于序列点数.复杂度 $O (n^{3}) > O (n \ln n) > O (n)$ , 即BPNN的时间复杂度最高, 其次为成型滤波法, 正弦波叠加法的时间复杂度最低.3种方法利用Matlab运行所需时间为正弦波叠加法为9.23 s, 成型滤波法为15.76 s, BPNN为27.30 s, 可看到BPNN所需的时间最长而正弦波叠加法所需的时间最短, 进一步验证利用BPNN仿真的计算量最大.这是由于BPNN需要反复学习训练过程, 使误差沿梯度方向下降, 牺牲了时间复杂度但提高了精度, 降低了仿真误差.但神经网络训练所需的时间与所采用的网络模型、误差逆向传播算法、待估参数数量、数据集大小等因素都有所关联.仿真时采用样本数为1 000的数据集进行训练预测, 其时间成本为27.30 s, 为成型滤波法的1.73倍, 而均方误差有较大的改善, 仿真结果已经较为理想, 因此时间成本在可接受范围内.

3.2 不同误差逆向传播算法效果对比

分别使用贝叶斯正则化(Bayesian regularization)算法和缩放共轭梯度(Scaled conjugate gradient)^[24]这两种算法来训练BP神经网络, 得到的均方差如图11所示.可以看到, 在相同训练次数前提下, 利用贝叶斯正则化算法训练BP神经网络得到的均方差为6.45× 10^-3(第998次), 利用缩放共轭梯度算法为9.17× 10^-3(第997次), 均高于由L-M算法训练的均方差1.43× 10^-4.因此L-M算法训练BP神经网络的精度更高.

	Figure Option View Download New Window
	图11 其他算法训练得到的均方差Fig.11 Mean square error obtained from training of other algorithms

贝叶斯正则化算法略优于缩放共轭梯度算法, 对于困难的、小的或有噪声的数据集可以产生良好的泛化能力, 但它通常需要更多的时间, 根据自适应权重最小化(正则化)停止训练.缩放共轭梯度算法训练需要的时间短, 因为其需要的内存较少.当泛化能力停止提高时, 训练会自动停止, 验证样本的均方误差会增加^[25].

4 结论

1)利用传统方法产生的大量多普勒功率谱样本数据, 训练神经网络对时变信道进行学习预测, 训练好的网络结构仿真出来的结果频域符合多普勒功率谱的特征, 呈U型谱.时域自相关函数满足第1类贝塞尔函数, 很好地符合Jakes模型的时频域条件, 均方误差达到1.43× 10^-4, 说明BP神经网络模型预测精度很高, 能较好地预测U型谱.理论上, 只要给神经网络输入足够样本数量的训练数据集进行充分学习, 训练好的网络模型即可用于预测具有更多影响因素的无线信道.

2)与传统的正弦波叠加法、成型滤波法仿真结果对比, 神经网络的仿真效果更接近理论值, 说明其效果优于传统方法, 同时具备具有很好的容错性.对3种方法的时间复杂度进行比较, 结果表明BPNN的时间复杂度最高为 $O (n^{3})$ .成型滤波法次之, 为 $O (n \ln n)$ .正弦波叠加法的时间复杂度最低, 为 $O (n)$ .BPNN的仿真误差最低, 但计算量较大, 牺牲了时间复杂度.

3)对3种误差逆向传播算法的仿真结果进行对比, 发现L-M算法训练BPNN的均方误差最低, 效果最佳.此外, 还对比了3种不同的误差逆向传播算法的预测效果, 仿真结果表明, L-M算法训练BP神经网络的精度最高, 贝叶斯正则化算法和缩放共轭梯度算法次之.

在后续研究中, 还将针对不同时变信道场景测试神经网络对其建模可行性及网络模型的可复用性.

参考文献

文献列表

[1]	CICHON D J, WIESBECK W. Ray optical wave propagation models for the characterization of radio channels in urban outdoor and indoor environments[C]// Military Communications Conference. McLean, 1996: 718-722. [本文引用:1]
[2]	王皎, 张彬, 李道本. 改进的JAKES的移动信道模型分析[C]//中国通信学会无线及移动通信委员会学术年会论文集, 2003: 372-377. WANG Jiao, ZHANG Bin, LI Daoben. Analyses of improved JAKES mobile communication channel models[C]//Proceedings of the Academic Annual Conference in China Institute of Communications, 2003: 372-377. (in Chinese) [本文引用:1]
[3]	WANG Q Y, LIU K Y, SUN Z G, et al. Research into the high-precision marine integrated navigation method using INS and star sensors based on time series forecasting BPNN[J]. Optik, 2018, 172: 494-508. [本文引用:1]
[4]	HE H T, WEN C K, JIN S, et al. Deep learning-based channel estimation for beamspace mmWave massive MIMO systems[J]. IEEE Wireless Communications Letters, 2018, 7(5): 852-855. [本文引用:1]
[5]	YE H, LI G Y, JUANG B H. Power of deep learning for channel estimation and signal detection in OFDM systems[J]. IEEE Wireless Communications Letters, 2018, 7(1): 114-117. [本文引用:1]
[6]	SAMUEL N, DISKIN T, WIESEL A. Deep MIMO detection[C]//18th International Workshop on Signal Processing Advances in Wireless Communications, Sapporo. 2017. [本文引用:1]
[7]	马永涛. 通信信道建模的神经网络优化技术研究[D]. 天津: 天津大学, 2009. MA Yongtao. Research on the neural networks optimization technique for communication channel modeling[D]. Tianjin: Tianjin University, 2009. (in Chinese) [本文引用:1]
[8]	SEZAVAR A, FARSI H, MOHAMADZADEH S. Content-based image retrieval by combining convolutional neural networks and sparse representation[J]. Multimedia Tools and Applications, 2019, 78(15): 20895-20912. [本文引用:1]
[9]	ZHU Y X, SUN W M, CAO X Y, et al. TA-CNN: Two-way attention models in deep convolutional neural network for plant recognition[J]. Neurocomputing, 2019, 365: 191-200. [本文引用:1]
[10]	朱玥, 覃尧, 董岚, 等. 人工智能在移动通信网络中的应用: 基于机器学习理论的信道估计与信号检测算法[J]. 信息通信技术, 2019, 13(1): 19-25. ZHU Yue, QIN Yao, DONG Lan, et al. Application cases of artificial intelligence in mobile communication networks: machine-learning-based channel estimator and signal detector[J]. Information and Communications Technologies, 2019, 13(1): 19-25. (in Chinese) [本文引用:1]
[11]	米杨, 张晓瀛, 魏急波. 三维模型中的多普勒功率谱分析[J]. 通信技术, 2015, 48(4): 404-409. MI Yang, ZHANG Xiaoying, WEI Jibo. Doppler power spectrum analysis in 3D model[J]. Communications Technology, 2015, 48(4): 404-409. (in Chinese) [本文引用:1]
[12]	WANG J, QIANG Y Q, ZHANG B, et al. Comparison of statistical properties between an improved Jakes’ model and the classical one[C]//14th IEEE Proceedings on Personal, Indoor and Mobile Radio Communications. Beijing, 2003: 1264298. [本文引用:1]
[13]	GIBERT X, PATEL V M, CHELLAPPA R. Deep multitask learning for railway track inspection[J]. IEEE Transactions on Intelligent Transportation Systems, 2017, 18(1): 153-164. [本文引用:1]
[14]	STALLKAMP J, SCHLIPSING M, SALMEN J, et al. Man vs. computer: Benchmarking machine learning algorithms for traffic sign recognition[J]. Neural Networks, 2012, 32: 323-332. [本文引用:1]
[15]	王玉环, 尹航, 杨占昕. 基于神经网络的信道译码算法研究综述[J]. 中国传媒大学学报(自然科学版), 2018, 25(3): 28-33. WANG Yuhuan, YIN Hang, YANG Zhanxin. A research review of channel decoding algorithm based on neural network[J]. Journal of Communication University of China(Science and Technology), 2018, 25(3): 28-33. (in Chinese) [本文引用:1]
[16]	陈敏华, 李杨, 张武雄. 基于卷积神经网络的信道均衡算法[J]. 计算机应用与软件, 2017, 34(9): 257-261. CHEN Minhua, LI Yang, ZHANG Wuxiong. Channel equalization algorithm based on convolutional neural network[J]. Computer Applications and Software, 2017, 34(9): 257-261. (in Chinese) [本文引用:1]
[17]	张宇飞, 沈瑶, 杨威, 等. 利用BP神经网络分析检测网络时序型隐信道[J]. 小型微型计算机系统, 2018, 39(5): 871-876. ZHANG Yufei, SHEN Yao, YANG Wei, et al. Detecting network covert timing channels using back-propagation neural network[J]. Journal of Chinese Computer Systems, 2018, 39(5): 871-876. (in Chinese) [本文引用:1]
[18]	张想, 李明齐, 王潮. 基于BP神经网络的短波通信信道预测方法[J]. 工业控制计算机, 2017, 30(10): 55-56. ZHANG Xiang, LI Mingqi, WANG Chao. A prediction method for HF communication channel based on BP neural network[J]. Industrial Control Computer, 2017, 30(10): 55-56. (in Chinese) [本文引用:1]
[19]	孙峰, 姚毅, 李成刚. LM算法在神经网络语音识别中的应用[J]. 科学技术与工程, 2011, 11(9): 2021-2024. SUN Feng, YAO Yi, LI Chenggang. Application of LM algorithm in neural network speech recognition[J]. Science Technology and Engineering, 2011, 11(9): 2021-2024. (in Chinese) [本文引用:1]
[20]	魏荣, 卢俊国, 王执铨. 基于Levenberg-Marquardt算法和最小二乘方法的小波网络混合学习算法[J]. 信息与控制, 2001, 30(5): 440-442. WEI Rong, LU Junguo, WANG Zhiquan. A hybrid learning algorithm based on levenberg-marquardt algorithm and least squares techniques for wavelet networks[J]. Information and Control, 2001, 30(5): 440-442. (in Chinese) [本文引用:1]
[21]	RUMELHART D E, HINTON G E, WILLIAMS R J. Learning representations by back-propagating errors[J]. Nature, 1986, 323(6088): 533-536. [本文引用:1]
[22]	AMARI S I. Backpropagation and stochastic gradient descent method[J]. Neurocomputing, 1993, 5(4/5): 185-196. [本文引用:1]
[23]	SUTSKEVER I, MARTENS J, DAHL G, et al. On the importance of initialization and momentum in deep learning[C]//Proceedings of the 30th International Conference on Machine Learning. Atlanta, 2013: 2176-2184. [本文引用:1]
[24]	南敬昌, 王梓琦, 高明明, 等. 超宽带滤波器的稀疏贝叶斯正则化逆向神经网络建模[J]. 计算机应用与软件, 2018, 35(10): 232-237. NAN Jingchang, WANG Ziqi, GAO Mingming, et al. Sparse Bayesian regularized inverse neural network modeling of uwbfilter[J]. Computer Applications and Software, 2018, 35(10): 232-237. (in Chinese) [本文引用:1]
[25]	李春念, 袁功林. 求解无约束问题的修正PRP共轭梯度算法[J]. 西南大学学报(自然科学版), 2018, 40(9): 67-75. LI Chunnian, YUAN Gonglin. A modified polak-ribière-polyak conjugate gradient algorithm for smooth convex programs[J]. Journal of Southwest University(Natural Science), 2018, 40(9): 67-75. (in Chinese) [本文引用:1]

1996

0.0

... 为在有限的频谱资源上尽可能地高质量、大容量传输有用信息,就要求设计者必须清楚地了解信道的特性,掌握电波在信道中的传播及变化规律,即建立精准的信道模型^[1] ...

2003

0.0

... 而小尺度衰落表征了接收信号短距离(几个波长)或短时间内的快速波动,是移动信道的主要特征,其中Clarke信道模型描述的小尺度平坦衰落信道中,移动台接收信号具有基于散射方式的场强统计特性,这正符合市区移动通信环境不存在直射路径的特点,其包络统计特性服从瑞利分布,因此又称为瑞利衰落信道模型^[2] ...

2018

0.0

... 但上述两种传统方法存在着种种缺陷,如:正弦波叠加法的精度较低,而成型滤波法的计算量较大,不适宜用于大数据量的信道仿真^[3] ...

2018

0.0

... 文献[4]基于神经网络对多径信道的输入输出响应进行了建模,讨论了建模的方法并给出了仿真的结果 ...

2018

0.0

... 文献[5]基于多层前向神经网络研究了时变信道建模方法,仿真结果表明前向神经网络可以很好地跟踪非稳态时变信道的特性 ...

2017

0.0

... 文献[6]基于深度学习搭建了深度MIMO(Multiple-Input Multiple-Output)检测器,将梯度投影法的迭代过程展开成深度神经网络,折中了算法的检测性能、复杂度与收敛性 ...

2009

0.0

... 利用神经网络学习预测时变信道模型,可以降低数据计算量,而且拥有高精度和强灵活性^[7] ...

2019

0.0

... 小尺度平坦衰落信道中^[8],由于周边散射物的影响,导致接收端接收到的是来自不同路径的多径信号 ...

2019

0.0

... 通常在具有瑞利衰落的环境下,多普勒功率谱用以描述接收信号功率随多普勒频率的变化,具有Jakes功率谱密度函数,即U型谱的特性,其表达式^[9]为 ...

2019

0.0

朱玥, 覃尧, 董岚, 等. 人工智能在移动通信网络中的应用: 基于机器学习理论的信道估计与信号检测算法[J]. 信息通信技术, 2019, 13(1): 19-25.

ZHU

Yue

, QIN

Yao

, DONG

Lan

, et al. Application cases of artificial intelligence in mobile communication networks: machine-learning-based channel estimator and signal detector[J]. Information and Communications Technologies, 2019, 13(1): 19-25. (in Chinese)

... 而两个高斯变量的平方和的根服从瑞利分布,因此包络服从瑞利分布^[10] ...

2015

0.0

... 正弦波叠加法易于实现、占用计算资源少,但是产生的多普勒功率谱是由多个离散频率点上的冲激构成,并且自相关性能不够理想,因而实际应用中常采用的是基于正弦叠加法的Jakes仿真模型^[11],其框图见图1 ...

2003

0.0

... 实部和虚部均是具有特定形状多普勒功率谱的高斯有色噪声,因此包络服从瑞利分布^[12] ...

2017

0.0

... y和x之间的映射关系可能是高度非线性和多维的,输入输出关系的数值模型会随着场景及影响因素的变化而发生改变,难以确定准确的模型^[13] ...

2012

0.0

... 其中x-y训练数据对,其可以通过测量得到,也可以通过精确地仿真得到^[14] ...

2018

0.0

... 根据Kolmogorov定理^[15],3层网络经过充分学习后能几乎逼近任何函数,所以建立如图4所示的3层结构的神经网络进行学习训练 ...

2017

0.0

... BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络,误差反向传播算法就是寻找合适 ω,b的一种思路^[16] ...

2018

0.0

... 当各层神经元的激活函数均采用sigmod函数,表达为^[17] ...

2017

0.0

... 确定与最小误差相对应的网络参数(权值和阈值),训练停止^[18] ...

2011

0.0

... 常见的误差逆向传播算法是梯度下降法,它是使用最广泛的最小二乘最优化算法^[19] ...

2001

0.0

魏荣, 卢俊国, 王执铨. 基于Levenberg-Marquardt算法和最小二乘方法的小波网络混合学习算法[J]. 信息与控制, 2001, 30(5): 440-442.

WEI

Rong

, LU

Junguo

, WANG

Zhiquan

. A hybrid learning algorithm based on levenberg-marquardt algorithm and least squares techniques for wavelet networks[J]. Information and Control, 2001, 30(5): 440-442. (in Chinese)

A hybrid learning algorithm for wavelet networks is presented to quicken up the speed of convergence, which combines the Levenberg-Marquardt (LM) algorithm with least squares methods. The LM algorithm trains a wavelet network over a reduced weight space that consists of nonlinear parameters of the wavelet networks. The remained weights that are linear parameters are calculated in accordance with least square methods. Identification of a chaotic system is applied to demonstration of the performance of the proposed hybrid learning algorithm. The results indicate that the proposed algorithm is very efficient and enables the learning process to significantly speed up.

Department of Automatic Control, Nanjing University of Science & Technology, Nanjing 210094

本文针对小波网络现有学习算法的不足，把Levenberg-Marquardt算法（简称LM算法）和最小二乘算法有机地结合在一起，提出了一种新的小波网络混合学习算法．在该混合算法中LM算法用来训练小波网络的非线性参数，而最小二乘算法用来训练线性参数．最后以辩识一个混沌系统为例进行了数值仿真，并与改进的BP算法和单纯LM算法进行了比较，结果说明了所提算法具有很好的收敛性能和收敛速度．

... 梯度下降法以负梯度方向作为极小化算法的下降方向,是无约束优化中最简单的方法,它具有储存量小、结构简单、易于实现等优点,但其缺点在于:在远离鞍点的地方下降很快,而在靠近鞍点的地方下降很慢,且损失函数可能收敛到鞍点^[20] ...

1986

0.0

... 高斯牛顿法的缺点在于:若初始点距离极小值点过远,迭代步长过大会导致迭代下一代的函数值不一定小于上一代的函数值^[21] ...

1993

0.0

... 在L-M算法中,每次迭代是寻找一个合适的阻尼因子 λ,当 λ很小时,算法就变成了高斯牛顿法的最优步长计算式, λ很大时,蜕化为梯度下降法的最优步长计算式,因此L-M算法介于牛顿法与梯度下降法之间,对于过参数化问题不敏感,能有效处理冗余参数问题,使代价函数陷入局部极小值的机会大大减小,这些特性使得L-M算法在图像识别等领域得到广泛应用^[22] ...

2013

0.0

... BPNN经由误差逆向传播算法训练,过程包括信号的正向传输及误差的反向传输,其时间复杂度为 O(n3),其中 n为网络节点数^[23] ...

2018

0.0

... 2 不同误差逆向传播算法效果对比分别使用贝叶斯正则化(Bayesian regularization)算法和缩放共轭梯度(Scaled conjugate gradient)^[24]这两种算法来训练BP神经网络,得到的均方差如图11所示 ...

2018

0.0

... 当泛化能力停止提高时,训练会自动停止,验证样本的均方误差会增加^[25] ...