基于随机矩阵理论的大规模MIMO系统窃听用户检测

引用本文

刘铭, 徐丽, 王晓懿, 陈佳奇. 基于随机矩阵理论的大规模MIMO系统窃听用户检测[J]. 北京交通大学学报, 2020,44(2): 58-65.
LIU Ming, XU Li, WANG Xiaoyi, CHEN Jiaqi. Active eavesdropper detection based on large dimension random matrix theory for massive MIMO systems[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2020,44(2): 58-65.
Doi:10.11860/j.issn.1673-0291.20190049 复制到剪切板

Permissions

北京交通大学学报编辑部所有

基于随机矩阵理论的大规模MIMO系统窃听用户检测

刘铭¹, 徐丽¹, 王晓懿², 陈佳奇³

1.北京交通大学计算机与信息技术学院,北京 100044

2.中铁第五勘察设计院集团有限公司,北京 102699

3.哈尔滨工业大学数学学院,哈尔滨 150006

第一作者:刘铭(1982—),男,陕西西安人,副教授,博士,博士生导师.研究方向为5G/B5G移动网络、物理层安全.email:mingliu@bjtu.edu.cn.

收稿日期: 2019-04-30

基金: 国家自然科学基金(61971029)

摘要

针对传统的利用信息论准则检测主动窃听用户方法的弊端,提出了适用于样本数目小于基站天线数目的检测主动窃听用户的算法.通过将线性收缩方法和子空间方法结合,有效地在小样本场景下进行主动窃听用户检测,而不产生额外的计算开销.提出利用大维随机矩阵理论获得对噪声方差更为精确的估计.同时采用线性收缩方法对样本协方差矩阵的特征值进行线性收缩,使其更好地拟合总体协方差矩阵,以提升小样本情况下的检测性能.最后利用子空间方法对线性收缩后的样本特征值进行检测,准确地检测是否存在主动窃听用户.蒙特卡洛仿真结果表明,结合大维随机矩阵理论与线性收缩的检测算法可以在小样本场景中有效检测主动窃听用户.

关键词: 无线通信; 大规模MIMO; 主动窃听用户检测; 随机矩阵理论; 线性收缩

中图分类号:TN92 文献标志码:A 文章编号:1673-0291(2020)02-0058-08

Active eavesdropper detection based on large dimension random matrix theory for massive MIMO systems

LIU Ming¹, XU Li¹, WANG Xiaoyi², CHEN Jiaqi³

1. School of Computer and Information Technology, Beijing Jiaotong University, Beijing 100044, China

2. China Railway Fifth Survey and Design Institute Group Co., Ltd., Beijing 102699, China

3. School of Mathematics, Harbin Institute of Technology, Harbin 150000, China

Fund:National Nature Science Foundation of China(61971029)

Abstract

According to the traditional method of using information theoretic approach to detect active eavesdropper, this paper proposes an algorithm for detecting active eavesdropper with a sample number smaller than the number of base station antennas. The proposed method combines the linear shrinkage method with the subspace method, and can detect active eavesdropper effectively when the number of samples is not large, without a significant increase of computational overhead. Specifically it proposes to employ the large-dimensional random matrix theory to obtain a more accurate estimate of noise variance. Linear shrinkage method is adopted to process the sample covariance matrix such that it can better fit the population covariance matrix and yield a better detection performance when the number of samples is not large. With the assistance of linearly shrinked sample covariance matrix, the subspace method is used to determine whether there exists active eavesdropper. The Monte Carlo simulation results show that the combination of large-dimensional random matrix theory and linear shrinkage detection algorithm can effectively detect the existence of the active eavesdropper when the number of samples is not large.

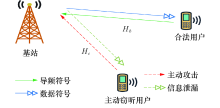
Keyword: wireless communication; massive MIMO; active eavesdropper detection; random matrix theory; linear shrinkage

文章图片

大规模MIMO(Massive Multiple-Input Multiple-Output)技术作为第五代移动通信网络(5G)的物理层关键技术, 具有前所未有的数据速率、频谱效率、能量效率、网络容量及更高的链路可靠性和覆盖范围^[1].然而, 因为无线通信环境的开放性, 大规模MIMO也存在一定的安全风险.大规模MIMO系统需要利用合法用户发送的导频信息估计下行信道的状态.在此过程中, 恶意用户可通过发送与合法用户相同的导频序列, 来误导基站的信道估计过程, 将下行链路信号波束引导到恶意用户的位置, 从而达到窃听的目的.该行为也被称为主动窃听攻击^[2].主动窃听攻击会严重地影响到无线通信环境的安全, 它将会阻塞合法用户的上行传输, 同时造成下行合法用户信息的泄漏^{[3, 4, 5]}.因此, 有必要研究适用于大规模MIMO系统的检测主动窃听攻击方法.

2012年, 文献[6]指出了采用时分双工(Time Division Duplex, TDD)体制的无线通信系统中可能存在主动窃听攻击问题.针对此问题, 不同研究者展开了一系列的相关研究.如:基于随机序列的检测算法^[7].基于信道统计的检测算法^[8]基于传输功率的检测算法^[9]和基于信号子空间的检测算法^[10].

现有的窃听用户检测算法大多是基于信息论准则进行窃听检测, 可以在用户单天线场景中有效地检测窃听用户, 但是在实际的用户多天线场景中检测性能较低.一般来说, 基于信息论准则的方法需要考虑样本特征值的分布.利用特征值分解(Eigen Value Decomposition, EVD)将样本协方差矩阵分解为信号子空间和噪声子空间.大的特征值对应的特征空间为信号空间, 小的特征值对应的特征空间为噪声空间.当基站天线数量保持固定而样本数量趋于无穷时, 该方法性能达到最佳.而在当基站天线数量大于样本数量的高维信号场景中, 信息理论准则方法的性能会严重恶化, 检测性能欠佳.

基于信号子空间的方法可较好地检测到主动窃听用户的存在.现有的基于信号子空间方法大多是当基站天线数量保持固定而样本数量趋于无穷时, 算法检测性能才能达到最佳.但是由于系统效率和成本的限制, 使用更小的样本进行窃听用户检测, 可带来更低的信号传输开销、时延和复杂度, 所以需要研究小样本场景下的主动窃听检测算法.而当样本数量小于基站天线数量, 即小样本场景时, 子空间算法的性能会严重恶化^[11].在经典情况下, 基站天线数目是固定的, 样本数趋于一个较大值, 样本协方差矩阵的特征值是总体协方差矩阵特征值的良好估计.因此, 在子空间方法中, 使用样本协方差矩阵的特征值, 可替代总体协方差矩阵的特征值.而对于高维问题, 矩阵的维度比样本的数量更大, 此时样本协方差矩阵的特征值不再是总体协方差矩阵特征值的良好估计.所以在小样本场景下使用子空间方法进行窃听用户检测时需要对样本协方差矩阵进行修正.

本文作者针对样本数小于基站天线数目的场景, 将大维随机矩阵理论(Random Matrix Theory, RMT)和线性收缩(Linear Shrinkage, LS)的方法相结合, 提出了一种基于大维随机矩阵理论-线性收缩(RMT-LS)的子空间窃听用户检测算法.

1 大规模MIMO系统主动窃听模型

本文中基站Alice和合法用户Bob工作在TDD模式下.假设大规模MIMO系统中存在主动窃听用户Eve.其中基站Alice具有几十至数百个( $M$ )天线, 每个合法用户Bob和主动窃听用户Eve分别配备数个( $K$ )天线.基站Alice和合法用户Bob之间会进行正常通信, 而主动窃听用户Eve则想要窃听Alice与Bob之间的通信.主动窃听原理如图1所示.合法用户尝试与基站建立无线链路.为此, Bob通过其天线向Alice发送一系列正交训练序列, 以便Alice能够基于这些已知序列来估计信道系数.Eve试图通过发送与Bob相同的训练序列来影响Alice的信道估计过程, 使得Alice估计得到的信道包含窃听用户的信道分量.此时, 在下行数据传输的过程中会有一部分信息泄漏到主动窃听用户处, 形成信息安全隐患.不失一般性的, 假设Eve拥有与Alice相同数量的天线.当主动窃听用户天线的数量小于合法用户天线的数量时, 窃听用户无法解调基站发送给合法用户的信息.当主动窃听用户天线的数量等于或大于合法用户天线的数量时, 可以有效地窃听合法用户的信息.但是, 窃听用户天线的数量越多, 就越容易被检测到.因此, 从窃听用户检测的角度, 本文考虑两者天线数量相等的情况.

	Figure Option View Download New Window
	图1 通信系统中主动窃听行为示意Fig.1 An illustration of active eavesdropping in massive MIMO-based systems

基于随机序列的主动窃听检测方法, 在训练序列之后发送一系列随机序列.Alice收到的来自Bob的随机序列表示为

$y_{b_{j}} = \sqrt[]{{p_{b}}^{t}} \sqrt[]{α} \overset{K}{\sum_{i = 1}} h_{b_{ji}} x_{b_{i}} + n_{b_{j}}$ (1)

当Eve对Bob所发送的随机序列施加污染时, Alice收到的随机序列可表示为

$\begin{matrix} y_{e_{j}} = \sqrt[]{{p_{b}}^{t}} \sqrt[]{α} \overset{K}{\sum_{i = 1}} h_{b_{ji}} x_{b_{i}} + \sqrt[]{{p_{e}}^{t}} \sqrt[]{β} \overset{K}{\sum_{i = 1}} h_{e_{ji}} x_{e_{i}} + n_{e_{j}} \end{matrix}$ (2)

式中: $x_{b_{i}}$ 和 $x_{e_{i}}$ 分别表示由第 $i$ 个发射天线从Bob和Eve发送的随机序列; 天线发送的随机序列 $x_{b_{i}}$ 的平均功率可以通过其二范数的形式表示为 $‖ x_{b} ‖_{F}^{2} = {[\overset{K}{\sum_{i = 1}} x_{b_{i}}^{2}]}^{1 / 2}; x_{e_{i}}$ 的平均功率可以通过其二范数的形式表示为 $‖ x_{e} ‖_{F}^{2} = {[\overset{K}{\sum_{i = 1}} x_{e_{i}}^{2}]}^{1 / 2}; y_{b_{j}}$ 和 $y_{e_{j}}$ 分别表示没有来自Eve的影响和有来自Eve的影响的由第 $j$ 个接收天线接收的随机序列; $h_{b_{ji}}$ 和 $h_{e_{ji}}$ 分别是Bob和Eve的第 $i$ 个发射天线与基站的第 $j$ 个接收天线之间的信道衰落系数; $α$ 和 $β$ 表示相关的路径损耗衰减因子; $p_{b}^{t}$ 和 $p_{e}^{t}$ 分别是Bob和Eve的上行链路传输功率; $n_{b_{j}}$ 和 $n_{e_{j}}$ 分别表示两种情况下的高斯噪声.通过窃听用户和合法用户分别传输随机序列, 可以形成不同的特征空间.如果窃听用户和合法用户传输完全相同的序列, 那么将无法从子空间上区分开两者.

以矩阵形式重写式(1)和式(2)可得

$Y_{b} = \sqrt[]{{p_{b}}^{t}} \sqrt[]{α} \tilde{H_{b}} X_{b} + N_{b} = \sqrt[]{p_{b}} \tilde{H_{b}} X_{b} + N_{b}$ (3)

$Y_{e} = \sqrt[]{{p_{b}}^{t}} \sqrt[]{α} \tilde{H_{b}} X_{b} + \sqrt[]{{p_{e}}^{t}} \sqrt[]{β} \tilde{H_{e}} X_{e} + N_{e} = \sqrt[]{p_{b}} \tilde{H_{b}} X_{b} + \sqrt[]{p_{e}} \tilde{H_{e}} X_{e} + N_{e}$ (4)

式中: $X_{b} \in C^{K \times T}$ 和 $X_{e} \in C^{K \times T}$ 是从Bob和Eve发送的随机序列, 序列长度为 $T$ ; $Y_{b} \in C^{M \times T}$ 和 $Y_{e} \in C^{M \times T}$ 分别是不存在来自Eve的污染时和存在来自Eve的污染时Alice所接收的序列; $\tilde{H_{b}} ~ CN (0, I_{M})$ 和 $\tilde{H_{e}} ~ CN (0, I_{M})$ 表示小尺度衰落, $I_{M}$ 是 $M \times 1$ 维单位矩阵. $p_{b} = α {p_{b}}^{t}$ 和 $p_{e} = β {p_{e}}^{t}$ 分别是合法用户和窃听用户的接收信号功率. $N_{b} \in C^{M \times T}$ 和 $N_{e} \in C^{M \times T}$ 表示两种情况下的高斯噪声.它们的元素是独立且同分布的复高斯随机变量, 其均值为0和方差为 $σ^{2}$ .假设基站可以通过长期观测准确估计噪声水平^{[12, 13]}.由于 $X_{b}$ 和 $X_{e}$ 是以一种独立的方式随机生成的, 他们将分别扩展 $K$ 维子空间.

令 $H_{b} = \sqrt[]{α} \tilde{H_{b}} \in C^{M \times K}$ 和 $H_{e} = \sqrt[]{β} \tilde{H_{e}} \in C^{M \times K} .$ 不失一般性的, 当有一个信号采样值时, 主动窃听检测问题可以通过以下假设检验来表征

$Η_{0} : y (t) = H_{b} (t) x_{b} (t) + n_{b} (t)$ (5)

${Η_{1} : y (t) = H_{b} (t) x_{b} (t) + H}_{e} (t) x_{e} (t) + n_{e} (t)$ (6)

式中: $y (t) = {[y_{1} (t), \dots, y_{M} (t)]}^{T} \in C^{M \times 1},$ 表示某一采样点上基站的接收信号序列. $x (t) = {[x_{1} (t), \dots, x_{K} (t)]}^{T} \in C^{K \times 1},$ 表示某一采样点上用户发送的随机序列. $H_{b} (t), H_{e} (t) \in C^{M \times K}$ 分别表示合法用户信道矩阵和窃听用户信道矩阵. $n_{b} (t), n_{e} (t) \in C^{M \times 1}$ 分别表示是否存在窃听用户两种情况下的高斯噪声向量.假设噪声 $n_{b} (t)$ 和 $n_{e} (t)$ 是独立同分布的复数高斯向量, 其均值为零和方差为 $σ^{2},$ 即 $n_{b} (t), n_{e} (t) ~ CN (0, σ^{2} I_{M})$ .其中原假设 $H_{0}$ 为系统中不存在主动窃听用户, 备择假设 $H_{1}$ 为系统中存在主动窃听用户.若接受原假设 $H_{0},$ 意味着接收信号中没有主动窃听用户.否则, 若接受备择假设 $H_{1},$ 表明该系统有可能被主动窃听.假设信道衰落系数在至少 $T$ 个连续采样周期上是恒定的.

接收信号也是独立且同分布的复高斯随机向量, 即 $y (t) ~ CN (0, D),$ 其中 $D$ 是总体协方差矩阵, $D = E [Y (t) Y^{H} (t)]$ .当只存在合法用户时, 总体协方差矩阵的特征值表示为 $l_{i}, i = 1, \dots, M$ . $l_{i}$ 为非递增序列, 即 $l_{1} \geq \dots \geq l_{K} \geq l_{K + 1} = \dots = l_{M} = σ^{2} .$ 在实际中, 只能通过计算样本协方差矩阵来近似总体协方差矩阵.样本协方差矩阵可以表示为 $R = (1 / T) \sum_{t}^{=} [y (t) y^{H} (t)]$ .对 $R$ 进行特征值分解, 得到样本协方差矩阵的特征值为 $λ_{1}, \dots, λ_{M},$ 其中 $λ_{1} \geq \dots \geq λ_{K} \geq λ_{K + 1} \geq \dots \geq λ_{M}$ .

2 基于随机矩阵理论的主动窃听检测

2.1 基于线性收缩算法改进样本协方差矩阵

经典的MDL(Minimum Description Length)检测算法可以表示为^[14]

$MDL (k) = T (M - k) \times \ln \frac{\frac{1}{M - k} \overset{M}{\sum_{i = k + 1}} λ_{i}}{(\overset{M}{\prod_{i = k + 1}} λ_{i})^{\frac{1}{M - k}}} + \frac{1}{2} k (2 M - k) \ln T$ (7)

式中: $k$ 是未知的用户天线数目; $T$ 是观测样本数; $M$ 是基站天线数目; $λ$ 是样本协方差矩阵的特征值.通过最小化式(7)可以得到合法用户数目 $K$ 的估计值.MDL方法只有当基站天线数目保持固定并且样本数量趋于无穷时才能达到最优, 在样本数小于基站天线数目时算法性能急剧下降.因为在样本数较小时, 样本特征值的分布范围明显偏离总体特征值的散布中心, 样本特征值不能很好地拟合总体特征值.所以, 本文利用统计理论中的线性收缩样本特征值的方法, 以改进传统的基于子空间方法的窃听检测算法, 使之适应于小样本的场景.

基于子空间的窃听检测算法思想是找到最小的 $M - K$ 个样本协方差矩阵的特征值, 即估计噪声特征值的个数.但是, 在小样本场景下, 噪声子空间的样本特征值散布的空间较大, 偏离了真实噪声特征值的分布范围.所以, 仅需对噪声子空间的样本协方差矩阵进行线性收缩, 优化噪声子空间的样本协方差矩阵的方差, 使其向真实的噪声方差趋近.将收缩后的噪声样本特征值带入MDL算法, 即可在小样本场景下准确的检测出主动窃听用户的存在.

利用Ledoit和Wolf(LW)方法求解线性收缩系数^[15], 求得噪声子空间的样本协方差矩阵的线性估计, 过程如下

$\min_{v} E [‖ {D_{n}}^{*} - D_{n} ‖_{F}^{2}]$ (8)

$s.t. D_{n}^{*} = v P_{n} + (1 - v) R_{n}$ (9)

式中: $‖ \cdot ‖_{F}^{2}$ 是平方Frobenius范数; $P_{n}$ 是一个由噪声方差构成的矩阵; $v$ 表示线性收缩系数; $D_{n}^{*}$ 是线性收缩后的噪声子空间的样本协方差矩阵, 表示为 $P_{n}$ 与噪声子空间的样本协方差矩阵 $R_{n}$ 的线性组合. $D_{n} = σ^{2} I_{M}$ 是噪声子空间的总体协方差矩阵.当 $M$ 、 $T \to \infty, c = T / M,$ 并且 $0 < c < \infty$ 时

$P_{n} = {\hat{σ}}^{2} I_{M - K}$ (10)

${\hat{R}}_{n} = diag (λ_{K + 1}, \dots, λ_{M})$ (11)

式中: ${\hat{σ}}^{2}$ 是噪声方差 $σ^{2}$ 的估计值; ${\hat{R}}_{n}$ 表示为 $R_{n}$ 的估计值.对 $R_{n}$ 进行特征值分解, 得到特征值为 $λ_{K + 1}, \dots, λ_{M}$ .因此, 可以使用对角线元素为 $λ_{K + 1}, \dots, λ_{M}$ 的对角矩阵 ${\hat{R}}_{n}$ 估计 $R_{n}$ .

LW方法给出了式(9)中存在的收缩系数为

$v = \frac{\overset{M}{\sum_{i = K + 1}} {λ_{i}}^{2} + {(\overset{M}{\sum_{i = K + 1}} λ_{i})}^{2}}{(T + 1) (\overset{M}{\sum_{i = K + 1}} {λ_{i}}^{2} - \frac{{(\overset{M}{\sum_{i = K + 1}} λ_{i})}^{2}}{M - K})}$ (12)

由于 $v$ 的取值可能大于 $1,$ 所以利用 $β = \min (v, 1)$ 作为样本协方差矩阵的收缩系数.因此, 噪声子空间的样本协方差矩阵最终可以被估计为

$D_{n}^{*} = β P_{n} + (1 - β) R_{n} ≜ diag (τ_{K + 1}, \dots, τ_{M})$ (13)

式中: $τ_{K + 1}, \dots, τ_{M}$ 表示优化矩阵的特征值, 即

$τ_{i} = β {\hat{σ}}^{2} + (1 - β) λ_{i}, i = K + 1, \dots, M$ (14)

通过将噪声子空间的样本特征值收缩到噪声方差, 进而得到优化后的样本协方差矩阵的特征值.

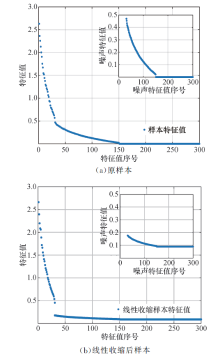
图2展示了本文算法对噪声子空间样本特征值的影响程度( $M = 300, K = 30, p_{b} = 1) .$ 当噪声方差 $σ^{2} = 0.1,$ 样本数为基站天线数目的一半时, 噪声样本特征值偏离实际噪声方差的程度较大.线性收缩后的噪声样本特征值更能拟合实际噪声方差.

	Figure Option View Download New Window
	图2 协方差矩阵的特征值分布Fig.2 Distribution of eigenvalues covariance matrix

在小样本的场景下, 噪声子空间的样本特征值散布的空间较大, 偏离了真实噪声特征值的分布范围, 即偏离了真实的噪声方差.本文对噪声子空间的样本协方差矩阵进行线性收缩, 使得样本协方差矩阵得到的噪声子空间的特征值向其真实的噪声方差趋近.图2(a)中噪声特征值偏离真实噪声方差(0.1)较远.而图2(b)中线性收缩后的噪声特征值在其真实方差(0.1)附近波动.说明线性收缩程度较好, 收缩后的样本特征值更能拟合真实的特征值分布.

2.2 基于大维随机矩阵理论的噪声方差估计

线性收缩方法中比较重要的一个环节是进行噪声方差估计, 传统的噪声估计方法^[14]中 $σ^{2}$ 的估计可以表示为

${\hat{σ}}_{0}^{2} = \frac{1}{M - K} \overset{M}{\sum_{i = K + 1}} λ_{i}$ (15)

传统的噪声估计方法首先对接收信号矩阵的特征值进行降序排序, 随后对排序后特征值序列的后 $M - K$ 个特征值进行求均值处理, 即可得到噪声方差的估计值.传统的噪声方差估计是基于用户单天线场景推导出的, 需要针对大规模MIMO场景提出新的噪声估计方法.本文将基于大维RMT中信号功率的估计方法, 推导出新的噪声方差估计方法.

首先, 定义基站接收的随机序列为 $Y \in C^{M \times T},$ 其样本协方差矩阵 $B_{N}$ 的有序特征值表示为 $λ = (λ_{1}, λ_{2}, \dots, λ_{M}), λ_{1} \geq \dots \geq λ_{M}$ .文献[16]中推导了用户发射功率 $p_{r}$ 的估计, 有以下定理.

定理1^[16]:定义样本协方差矩阵 $B_{N} = (1 / T) Y Y^{H},$ 用户发射功率 $p_{r}$ 的估计表示为

${\hat{p}}_{r} = \frac{MT}{n_{r} (T - M)} \sum_{i \in N_{r}} (η_{i} - μ_{i})$ (16)

$N_{r} = \{1 + \overset{r - 1}{\sum_{j = 1}} n_{j}, 2 + \overset{r - 1}{\sum_{j = 1}} n_{j}, \dots, n_{r} - 1 + \overset{r - 1}{\sum_{j = 1}} n_{j}, \overset{r}{\sum_{j = 1}} n_{j}\}$ (17)

$η = (η_{1}, \dots, η_{M}) = eig (diag (λ) - \frac{1}{M} \sqrt[]{λ} {\sqrt[]{λ}}^{T})$ (18)

$μ = (μ_{1}, \dots, μ_{M}) = eig (diag (λ) - \frac{1}{T} \sqrt[]{λ} {\sqrt[]{λ}}^{T})$ (19)

式中:r表示合法用户, r=1, 2, …, L; $n_{r}$ 表示第 $r$ 个合法用户的天线数目; $K = n_{1} + n_{2} + \dots + n_{L} .$

举例说明 $i$ 的取值范围, 当存在3个合法用户时, 假定合法用户1的天线数目等于3, 合法用户2的天线数目等于4, 合法用户3的天线数目等于5, 即 $r = 3, n_{1} = 3, n_{2} = 4, n_{3} = 5$ 时

$N_{1} = \{1, 2, \dots, n_{1} - 1, \overset{1}{\sum_{j = 1}} n_{j}\}$ (20)

$N_{2} = \{1 + \overset{1}{\sum_{j = 1}} n_{j}, 2 + \overset{1}{\sum_{j = 1}} n_{j}, \dots, n_{2} - 1 + \overset{1}{\sum_{j = 1}} n_{j}, \overset{2}{\sum_{j = 1}} n_{j}\}$ (21)

$N_{3} = \{1 + \overset{2}{\sum_{j = 1}} n_{j}, 2 + \overset{2}{\sum_{j = 1}} n_{j}, \dots, n_{3} - 1 + \overset{2}{\sum_{j = 1}} n_{j}, \overset{3}{\sum_{j = 1}} n_{j}\}$ (22)

即 $N_{1} = \{1, 2, n_{1}\} = \{1, 2, 3\}, N_{2} = {n_{1} + 1, n_{1} + 2, \dots, n_{1} + n_{2} - 1, n_{1} + n_{2}} = {4, 5, 6, 7}, N_{3} = {n_{1} + n_{2} + 1, n_{1} + n_{2} + 2, \dots, n_{1} + n_{2} + n_{3} - 1, n_{1} + n_{2} + n_{3}} = {8, 9, 10, 11, 12} .$

对于估计方法中存在的 $η$ 和 $μ$ 向量, 在此给出简要的解释.其中eig表示求取特征值的函数. $η_{1}, \dots, η_{M}$ 是矩阵 $diag (λ) - 1 / M \sqrt[]{λ} {\sqrt[]{λ}}^{T}$ 的有序特征值, 也是 $m (z) = 0$ 的 $M$ 个实数根, 即 $z$ 的解. $μ_{1}, \dots, μ_{M}$ 是矩阵 $diag (λ) - 1 / T \sqrt[]{λ} {\sqrt[]{λ}}^{T}$ 的有序特征值, 也是 $m' (z) = 0$ 的 $M$ 个实数根, 即 $z$ 的解.其中, $m (z)$ 和 $m' (z)$ 分别为 $B_{N}$ 和 $B_{N}^{*}$ 的经验谱分布的Stieltjes变换, $B_{N}^{*}$ 为 $B_{N}$ 的伴随阵. $B_{N}$ 的经验谱分布的Stieltjes变换 $m (z)$ 的积分形式为

$m (z) = \int \frac{1}{λ - z} d Q (λ)$ (23)

式(16)表示存在多个合法用户时信号功率的估计.考虑只存在一个合法用户, 即 $r = 1, p_{1} = p_{b}, n_{1} = K$ 时, 功率 $p_{b}$ 的估计可以表示为

${\hat{p}}_{b} = \frac{MT}{K (T - M)} \sum_{i \in N_{1}} (η_{i} - μ_{i})$ (24)

式中: $N_{1} = \{1, 2, \dots, K - 1, K\} .$

以上是根据大维RMT中Stieltjes变换推导得到的 ${\hat{p}}_{b}$ .从而推导出噪声方差 $σ^{2}$ 的估计为

${\hat{σ}}^{2} = \frac{MT}{(M - K) (T - M)} \sum_{i \in N} (η_{i} - μ_{i})$ (25)

式中: $N = \{1 + \overset{r}{\sum_{j = 1}} n_{j}, 2 + \overset{r}{\sum_{j = 1}} n_{j}, \dots, M - 1, M\} .$

证明:定义 $c_{r} = M / n_{r},$ 表示基站天线数目和合法用户天线数目的比值.合法用户 $p_{r}$ 表示为

$p_{r} = \frac{c_{r}}{c} \frac{1}{2 π i} \oint_{C} \int \frac{w}{z - w} d H (z) d w$ (26)

对积分进行离散化, 得到

$p_{r} = c_{r} \frac{1}{2 π i} \oint_{C} \overset{K}{\sum_{r = 1}} \frac{1}{c_{r}} \frac{w}{p_{r} - w} d w$ (27)

$p_{0} = c_{0} \frac{1}{2 π i} \oint_{C} \overset{K}{\sum_{r = 1}} \frac{1}{c_{r}} \frac{w}{p_{r} - w} d w$ (28)

$c_{0} = \frac{M}{M - K}$ (29)

式中: $p_{0} 为噪声功率,$ 在对合法用户功率进行估计过程中, $p_{r}$ 的系数由 $M / n_{r}$ 变为 $MT / [n_{r} (T - M)]$ .同理, 噪声方差估计值的系数将由 $M / (M - K)$ 变为 $MT / [(M - K) (T - M)],$ 因此

$N = {n_{1} + n_{2} + n_{3} + 1, n_{1} + n_{2} + n_{3} + 2, \dots, M - 1, M} = {13, 14, \dots, M - 1, M} .$

当只存在一个合法用户, 即 $r = 1, p_{1} = p_{b}, n_{1} = K$ 时

$\begin{array}{l} N = {n_{1} + 1, n_{1} + 2, \dots, M - 1, M} = \\ {K + 1, K + 2, \dots, M - 1, M}, \\ i \in \{K + 1, K + 2, \dots, M - 1, M\} . \end{array}$

2.3 结合线性收缩与大维随机矩阵的窃听检测

本节将大维RMT与线性收缩样本特征值的方法相结合, 设计了窃听用户检测算法.将式(14)中求得的线性收缩后的特征值带入MDL算法式(7)中, 并改变其惩罚项, 得到重新定义后的MDL算法为

$R L_{MDL} (k) = T (M - k) \ln \frac{\frac{1}{M - k} \overset{M}{\sum_{i = k + 1}} τ_{i}}{(\overset{M}{\prod_{i = k + 1}} τ_{i})^{\frac{1}{M - k}}} + \frac{1}{2} k (2 M - k) \lg T$ (30)

式中: $τ_{i}$ 表示样本协方差矩阵优化矩阵的特征值.

通过最小化式(31)得到窃听用户检测算法的检验统计量

$\overset{\land}{k} = \arg \min_{1 \leq k \leq M - 1} R L_{MDL} (k)$ (31)

根据式(31)中得到的检验统计量, 将假设式(5)和式(6)重新表述为

$H_{0} : k = K$ (32)

$H_{1} : k > K$ (33)

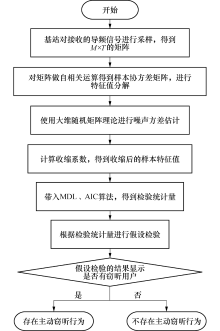
在假设检验中, 如果 $k = K,$ 接受原假设, 说明系统没有受到主动窃听用户的攻击; 如果 $k > K,$ 接受备择假设, 说明系统受到主动窃听用户的攻击.

3 性能评估

大维RMT与线性收缩方法相结合的子空间窃听用户检测算法具体实施步骤, 如图3所示.

	Figure Option View Download New Window
	图3 主动窃听检测算法流程Fig.3 Flow chart of the active eavesdropper detection

本节对式(31)提出的基于大维RMT-LS的子空间检测算法进行仿真实验, 展示了在不同天线数目、样本数、信号功率和信噪比环境下算法的检测性能曲线.并在最后仿真了基于大维RMT进行参数估计的算法和传统的参数估计方法对窃听检测的影响.对于每一次仿真实现, 信道系数服从复高斯分布, 其均值为0, 方差为1.加性白噪声服从复高斯分布, 其均值为0, 方差为 $σ^{2}$ .本文中考虑了大规模MIMO场景, 信噪比的计算公式如下

$S_{NR} = \frac{K p_{b}}{σ^{2}}$ (34)

仿真实验中根据检测概率和虚警概率评估算法性能.检测概率表示系统存在窃听用户时, 检测算法能够检测到窃听用户的概率.虚警概率表示系统中不存在窃听用户时, 检测算法错误地检测到窃听用户的概率.因此, 高检测概率和低虚警概率是检测算法的期望目标.

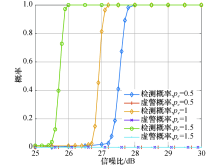图4展示了在不同的主动窃听用户与合法用户信号功率比值( $p_{e} / p_{b}$ )的条件下, 算法检测性能随信噪比变化的曲线 $(p_{b} = 1, T = 200, M = 300, K = 16),$ 可以得出:本文所提出的算法检测概率随着SNR增加而上升, 直到趋向于1.同时, 可以在比较低的 $p_{e} / p_{b}$ (如0.5)比率下工作.当窃听用户信号功率 $p_{e}$ 从0.5增加到1.5时, 检测性能约改善2 dB.说明当主动窃听用户的信号功率增加时, 算法的检测性能逐渐增强, 可以更准确地检测出主动窃听用户.即窃听用户增加信号功率时可以更容易地检测到它的存在.当窃听用户信号功率低于合法用户信号功率时, 检测性能会略有下降.需要说明的是, 虽然窃听用户可能会通过降低自己的发射功率来逃避本文算法的窃听检测.但是, 当窃听用户通过降低其发射功率来逃避检测时会造成接收信噪比的降低.所以, 窃听用户不会减少自己的信号功率.因此, 证明了本文检测算法的有效性.

	Figure Option View Download New Window
	图4 功率和合法用户信号功率对算法检测性能的影响Fig.4 Effect of eavesdropper’ s signal and legitimate user’ s signal power on detection performance

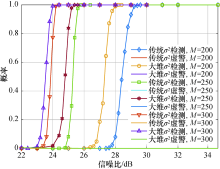图5展示了在不同的天线数目 $M$ 的条件下, 算法检测性能随信噪比的变化可以得出:算法检测概率随SNR增加而上升, 直到趋向于1.说明在高SNR时, 可以准确发现窃听用户的存在.当 $M$ 从200增加到300时, 检测性能约改善4 dB.即当“ 天线-采样比” 固定时, 检测概率随着基站天线数的增加而增加, 虚警概率趋近于零.将本文的大维 $σ^{2}$ 检测算法和 $σ^{2}$ 检测算法进行了对比.当样本数小于基站天线数目时, 使用本文提出的大维RMT进行噪声方差估计的检测算法, 检测窃听用户的能力更强.使用传统的噪声方差估计的检测算法, 需要更高的信噪比才能准确地检测到主动窃听用户的存在. $M = 200$ 时, 大维 $σ^{2}$ 检测算法可以比 $σ^{2}$ 检测算法多获得约1.3 dB的性能增益. $M = 250$ 时, 大维 $σ^{2}$ 检测算法可以比 $σ^{2}$ 检测算法多获得约0.8 dB的性能增益.对比不同基站天线数目的情况可看出, 随着基站天线数目的减少, $σ^{2}$ 检测算法检测性能显著下降, 大维 $σ^{2}$ 检测算法的优越性更加明显.这是因为传统的噪声估计方法是基于用户单天线场景推导出的, 而本文的噪声估计方法是基于矩阵维度较大的大维RMT推导出的, 更加适用于大规模MIMO场景.

	Figure Option View Download New Window
	图5 基站天线数目对不同算法检测性能的影响Fig.5 Effect of the number of base station antennas on detection performance of different algorithms

图6展示了在不同样本数 $T$ 的条件下, 算法检测性能随信噪比变化的曲线.

	Figure Option View Download New Window
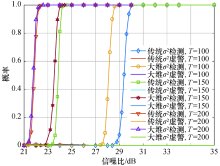	图6 样本数对不同算法检测性能的影响Fig.6 Effect of the sample number on detection performance of different algorithms

可以得出:算法检测概率随着SNR增加而上升, 直到趋向于1.当样本数从100增加到150时, 检测性能约改善4.5 dB.即当基站天线数固定时, 检测概率随着“ 天线-采样比” 的减少而增加, 虚警概率趋近于零.在样本数小于基站天线数时, 增加样本数, 算法的检测性能随之增强.对比发现, 随着信噪比和样本数目的增加, 两种算法的检测性能都随之增强. $T = 100$ 时, 大维 $σ^{2}$ 检测算法可以比 $σ^{2}$ 检测算法多获得约1.5 dB的性能增益, 验证了通过大维RMT进行噪声方差估计的方法可以增强算法的检测性能.同时, 样本数越小, 使用本文提出的大维RMT进行噪声方差估计的算法, 检测主动窃听用户的能力更强.需要指出的是, 本文算法可以在样本较小的情况下(样本数仅为基站天线数的一半), 检测出主动窃听用户的存在, 极大地改善了传统的检测算法只适用于样本数大于基站天线数的情况.因为随着MIMO的发展, 系统中的天线数目将越来越多, 针对小样本场景的窃听检测算法将会有更广阔的应用空间.

4 结论

1)提出一种基于大维RMT-线性收缩的主动窃听用户检测算法.利用大维RMT, 对特征值的分布函数进行Stieltjes变换, 求得噪声方差的估计值.

2)将估计得到的噪声方差用于线性收缩方法, 收缩样本特征值, 使其更好地拟合总体特征值.再次, 利用线性收缩算法得到噪声子空间分量的协方差矩阵的精确估计, 将线性收缩后的噪声特征值用于传统的信息论准则算法, 从而得到检验统计量进行假设检验.

3)对基于大维RMT-线性收缩用于窃听用户检测的算法进行蒙特卡洛仿真, 实验结果表明算法具有较高的检测概率和较低的虚警概率.

4)算法在小样本场景下可以达到有效检测窃听用户的效果.并且检测性能随着样本数、基站天线数目和信号功率的增加得到改善显著.同时, 算法可以适用于多种传统的基于子空间方法的窃听用户检测, 拓展了算法的应用场景.

参考文献

文献列表

[1]	SHAFI M, MOLISCH A F, SMITH P J, et al. 5G: A tutorial overview of stand ards, trials, challenges, deployment and practice[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(6): 1201-1221. [本文引用:1]
[2]	KAPETANOVIC D, ZHENG G, WONG K K, et al. Detection of pilot contamination attack using rand om training and massive MIMO[C]// Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications. London, 2013: 13-18. [本文引用:1]
[3]	DENG R, ZHOU S, NIU Z. Scalable non-orthogonal pilot design for massive MIMO systems with massive connectivity[C]// IEEE Global Communications Conference Workshops. Washington DC, 2017: 1-6. [本文引用:1]
[4]	HU D, ZHANG W, HE L, et al. Secure transmission in multi-cell multi-user massive MIMO systems with an active eavesdropper[J]. IEEE Wireless Communications Letters, 2019, 8(1): 85-88. [本文引用:1]
[5]	TIMILSINA S, BADUGEG A A, SCHAEFER R F. Secure communication in spectrum-sharing massive MIMO systems with active eavesdropping[J]. IEEE Transactions on Cognitive Communications & Networking, 2018, 4(2): 390-405. [本文引用:1]
[6]	ZHOU X, MAHAM B, HJØRUNGNES A. Pilot contamination for active eavesdropping[J]. IEEE Transactions on Wireless Communications, 2012, 11(3): 903-907. [本文引用:1]
[7]	WANG X, LIU M, WANG D, et al. Pilot contamination attack detection using rand om symbols for massive MIMO systems[C]// IEEE 85th Vehicular Technology Conference. Sydney, 2017: 1-7. [本文引用:1]
[8]	FLORDELIS J, GAO X, DAHMAN G, et al. Spatial separation of closely-spaced users in measured massive multi-user MIMO channels[C]// IEEE International Conference on Communication. London, 2015: 1441-1446. [本文引用:1]
[9]	XIONG Q, LIANG Y C, LI K H, et al. An energy-ratio-based approach for detecting pilot spoofing attack in multiple-antenna systems[J]. IEEE Transactions on Information Forensics and Security, 2015, 10(5): 932-940. [本文引用:1]
[10]	TUGNAIT J K. Self-contamination for detection of pilot contamination attack in multiple antenna systems[J]. IEEE Wireless Communications Letters, 2015, 4(5): 525-528. [本文引用:1]
[11]	LEDOIT O, WOLF M. A well-conditioned estimator for large-dimensional covariance matrices[J]. Journal of Multivariate Analysis, 2004, 88(2): 365-41. [本文引用:1]
[12]	COON J, SANDELL M, BEACH M, et al. Channel and noise variance estimation and tracking algorithms for unique-word based single-carrier systems[J]. IEEE Transactions on Wireless Communications, 2006, 5(6): 1488-1496. [本文引用:1]
[13]	DAS A, RAO B D. SNR and noise variance estimation for MIMO systems[J]. IEEE Transactions on Signal Processing, 2012, 60(8): 3929-3941. [本文引用:1]
[14]	WAX M, KAILATH T. Detection of signals by information theoretic criteria[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1985, 33(2): 387-392. [本文引用:2]
[15]	HUANG L, SO H C. Source enumeration via MDL criterion based on linear shrinkage estimation of noise subspace covariance matrix[J]. IEEE Transactions on Signal Processing, 2013, 61(19): 4806-4821. [本文引用:1]
[16]	COUILLET R, SILVERSTEIN J W, BAI Z, et al. Eigen-inference for energy estimation of multiple sources[J]. IEEE Transactions on Information Theory, 2010, 57(4): 2420-2439. [本文引用:2]

2017

0.0

... 大规模MIMO(Massive Multiple-Input Multiple-Output)技术作为第五代移动通信网络(5G)的物理层关键技术,具有前所未有的数据速率、频谱效率、能量效率、网络容量及更高的链路可靠性和覆盖范围^[1] ...

2013

0.0

... 该行为也被称为主动窃听攻击^[2] ...

2017

0.0

... 主动窃听攻击会严重地影响到无线通信环境的安全,它将会阻塞合法用户的上行传输,同时造成下行合法用户信息的泄漏^[3,4,5] ...

2019

0.0

... 主动窃听攻击会严重地影响到无线通信环境的安全,它将会阻塞合法用户的上行传输,同时造成下行合法用户信息的泄漏^[3,4,5] ...

2018

0.0

... 主动窃听攻击会严重地影响到无线通信环境的安全,它将会阻塞合法用户的上行传输,同时造成下行合法用户信息的泄漏^[3,4,5] ...

2012

0.0

... 2012年,文献[6]指出了采用时分双工(Time Division Duplex,TDD)体制的无线通信系统中可能存在主动窃听攻击问题 ...

2017

0.0

... 如:基于随机序列的检测算法^[7] ...

2015

0.0

... 基于信道统计的检测算法^[8]基于传输功率的检测算法^[9]和基于信号子空间的检测算法^[10] ...

2015

0.0

... 基于信道统计的检测算法^[8]基于传输功率的检测算法^[9]和基于信号子空间的检测算法^[10] ...

2015

0.0

... 基于信道统计的检测算法^[8]基于传输功率的检测算法^[9]和基于信号子空间的检测算法^[10] ...

2004

0.0

... 而当样本数量小于基站天线数量,即小样本场景时,子空间算法的性能会严重恶化^[11] ...

2006

0.0

... 假设基站可以通过长期观测准确估计噪声水平^[12,13] ...

2012

0.0

... 假设基站可以通过长期观测准确估计噪声水平^[12,13] ...

1985

0.0

... 1 基于线性收缩算法改进样本协方差矩阵经典的MDL(Minimum Description Length)检测算法可以表示为^[14] ...

... 2 基于大维随机矩阵理论的噪声方差估计线性收缩方法中比较重要的一个环节是进行噪声方差估计,传统的噪声估计方法^[14]中 σ2的估计可以表示为 ...

2013

0.0

... 利用Ledoit和Wolf(LW)方法求解线性收缩系数^[15],求得噪声子空间的样本协方差矩阵的线性估计,过程如下 ...

2010

0.0

... 文献[16]中推导了用户发射功率 pr的估计,有以下定理 ...

... 定理1^[16]:定义样本协方差矩阵 BN=(1/T)YYH,用户发射功率 pr的估计表示为 ...