考虑轴承游隙变化的高速列车牵引电机轴承疲劳寿命分析

引用本文

耿民, 徐涛, 邱超军, 赵波, 王华巍, 王喜莲. 考虑轴承游隙变化的高速列车牵引电机轴承疲劳寿命分析[J]. 北京交通大学学报, 2020,44(2): 136-142.
GENG Min, XU Tao, QIU Chaojun, ZHAO Bo, WANG Huawei, WANG Xilian. Fatigue life analysis of high-speed train traction motor bearing considering the change of bearing clearance[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2020,44(2): 136-142.
Doi:10.11860/j.issn.1673-0291.20190087 复制到剪切板

Permissions

北京交通大学学报编辑部所有

考虑轴承游隙变化的高速列车牵引电机轴承疲劳寿命分析

耿民¹, 徐涛², 邱超军¹, 赵波¹, 王华巍², 王喜莲²

1.中车唐山机车车辆有限公司动车检修部,河北唐山 063035

2.北京交通大学电气工程学院,北京 100044

通信作者:邱超军(1990—),男,河北唐山人,工程师,硕士.email:qiuchaojun.ts@crrcgc.cc.

第一作者:耿民(1980—),男,河北唐山人,高级工程师.研究方向为高速动车组牵引系统.email:gengmin@tangche.com.

收稿日期: 2019-08-29

基金: 国家自然科学基金(51178026)

摘要

高速列车牵引电机轴承的游隙在运行过程中不断变化,游隙变化造成电机转子偏心量波动,从而引起转子偏心磁拉力变化造成轴承载荷变化,导致轴承疲劳寿命下降,造成行车安全隐患.围绕高速列车牵引电机轴承游隙变化情况下的疲劳寿命进行分析,介绍了滚动轴承疲劳寿命计算理论的研究现状和两种常用的寿命计算模型,分析了高速列车牵引电机轴承受载荷情况,并搭建ANSYS接触仿真模型,考虑游隙变化带来的载荷变化和应力集中效应,提出了一种改进的疲劳寿命计算方法,对疲劳寿命进行更为精确的计算.编制改进疲劳寿命计算方法的Matlab程序,与经典L-P方法和ISO计算方法作对比,并搭建了以轴承游隙为输入参数的轴承疲劳寿命计算平台.

关键词: 高速列车; 滚子轴承; 轴承游隙; 载荷分布; 疲劳寿命; 仿真分析

中图分类号:TH133.3 文献标志码:A 文章编号:1673-0291(2020)02-0136-07

Fatigue life analysis of high-speed train traction motor bearing considering the change of bearing clearance

GENG Min¹, XU Tao², QIU Chaojun¹, ZHAO Bo¹, WANG Huawei², WANG Xilian²

1. Motor Vehicle Maintenance Department, CRRC Tangshan Co., Ltd., Tangshan Hebei 063035, China

2. School of Electrical Engineering, Beijing Jiaotong University, Beijing 100044, China

Fund:National Natural Science Foundation of China(51178026)

Abstract

The clearance of high-speed train traction motor bearing changes constantly in the operation process. The change of clearance causes the fluctuation of the eccentric magnetic pull of motor rotor, which leads to the decrease of bearing fatigue life and hidden danger of driving safety. In this paper, the relationship between clearance change and fatigue life of bearings of high-speed train traction motor is analyzed. First, the development history of fatigue life calculation theory of rolling bearings and two commonly used life models are introduced. Then, the load on bearings of high-speed train traction motor is analyzed and the ANSYS contact simulation model is built. Therefore, an improved fatigue life calculation method is proposed in this paper, it considers the load change and stress concentration effect caused by the change of clearance. Finally, the classical L-P method, ISO calculation method and the improved fatigue life calculation method proposed in this paper are compared in Matlab, and a bearing fatigue life calculation platform with bearing clearance as input parameter is built.

Keyword: high-speed train; roller bearing; bearing clearance; load distribution; fatigue life; simulation analysis

文章图片

我国高速铁路事业近年来发展迅猛, 各个领域的科学研究和技术革新不断进行.在高速列车动力系统中, 滚动轴承作为重要的旋转机械零部件起到了至关重要的作用^[1], 而高速列车运行环境复杂且速度较高, 因此高速列车牵引电机轴承也易损坏.目前高速列车定时厂修时会对轴承进行检修和维护, 但轴承检修程序繁琐, 且由于轴承过早更换将造成资源浪费, 或未及时更换将带来安全隐患.改善现有的定时维护机制并向智能维护机制过渡, 准确预测轴承疲劳寿命是关键.

滚动轴承工作环境复杂, 由于材料、安装使用不当等原因, 会出现多种形式的失效^[2], 其中滚动接触疲劳最为典型^[3].早期, 基于大量滚动轴承的疲劳试验可以预测轴承的寿命^[4], 理论和实践结果证明轴承的疲劳寿命服从Weibull分布, 而后Lundberg和Palmgren基于Weibull理论, 利用Hertz弹性接触理论计算出滚动承受的最大接触应力, 再结合额定动载荷理论计算出轴承疲劳寿命, 创立了L-P寿命计算模型^[5].1962年, ISO将原始的L-P寿命公式列为推荐标准ISO/R281/1-1962^[6].而后, 文献[7]说明了应用材料疲劳破坏极限与离散有限元体积法修正了L-P理论, 简称为 I-H 理论.文献[8]考虑了轴承内表面法向力和切向力的情况下, 综合轴承寿命实验的研究成果进一步充实了L-P理论.而在应用L-P理论进行实际计算时, 考虑了轴承材料、润滑、污染、游隙等对轴承疲劳寿命的影响, 引入了寿命修正系数.ISO/TS16281^[9]中给出了 $α_{ISO}$ 的计算方法, $α_{ISO}$ 是一个与环境污染系数、黏度比、静态额定载荷和动态载荷有关的寿命修正系数, 用它对基本额定疲劳寿命修正后能得到更加符合现场环境和轴承状态的疲劳寿命估计.

轴承在实际运行过程中, 可能会出现不对中、游隙变化等情况, 滚动轴承中的径向游隙对轴承疲劳寿命有重大影响作用^[10], 文献[11]在L-P理论的基础上, 研究了过盈配合、初始游隙、弯矩、温度及残余应力对疲劳寿命的影响, 建立了滚子轴承疲劳寿命的修正计算模型.文献[12]分别使用有限元方法、Harris方法和静力学方法分析了游隙对轴承内部载荷分布情况的影响, 发现游隙变化时, 载荷分布及最大接触载荷受到影响, 游隙增大时, 承载滚子数减少, 最大接触载荷增大.文献[13]将径向游隙看作最小油膜厚度, 添加寿命润滑修正系数进行滚动轴承寿命的计算.文献[14]对滚动轴承不同游隙时轴承的载荷分布和疲劳寿命情况做了很多研究, 发现轴承游隙变化确实会对疲劳寿命产生影响.

本文作者在计算轴承疲劳寿命的过程中考虑到游隙变化造成的影响, 提出了改进的滚动轴承疲劳寿命计算方法, 并与几种常用的寿命计算方法进行实验对比.最后采用牵引电机基础参数、滚动轴承基础参数和轴承游隙参数作为输入, 建立了高速列车牵引电机转子轴承疲劳寿命计算平台.

1 轴承疲劳寿命计算模型

针对高速列车牵引电机轴承游隙变化时的疲劳寿命进行分析, 首先对轴承疲劳寿命的常用计算模型进行研究, 进而考虑轴承游隙变化时对疲劳寿命计算模型的修正.滚动轴承疲劳计算发展至今, 众多经验和理论模型在各个领域均有应用, 其中, 以经典L-P寿命理论模型和ISO计算模型应用较为广泛.

1.1 经典L-P模型

经典L-P模型^[5]假设位于表面下某处深度的最大正交剪应力导致了裂纹产生, 进而主导了轴承失效.其载荷-寿命方程式如下

$L_{μ} = {(\frac{Q_{cμ}}{Q_{eμ}})}^{3}$ (1)

$L_{ν} = {(\frac{Q_{cν}}{Q_{eν}})}^{3}$ (2)

$L = {(L_{μ}^{- e} + L_{ν}^{- e})}^{- \frac{1}{e}}$ (3)

式中: $Q_{cμ}$ 为内滚道额定动载荷; $Q_{eμ}$ 为内滚道当量动载荷; e为Weibull斜率; $L_{μ}$ 为内滚道寿命; $L_{ν}$ 为外滚道寿命; $L$ 为轴承整体寿命, 轴承疲劳寿命通过内外滚道寿命进行加权计算得到.

1.2 ISO计算模型

ISO对基于L-P理论的寿命计算进行修正, 加入可靠性、材料和运行条件这3个修正系数得到修正疲劳寿命^[15], 计算公式如下

$L_{ISO} = a_{1} a_{2} a_{3} L_{10} = a_{1} a_{2} a_{3} {(\frac{C}{P})}^{p}$ (4)

式中: $L_{10}$ 为失效概率为10%时的基本额定寿命; $p$ 为载荷-寿命系数, 球轴承取3, 滚子轴承取10/3; $a_{1}$ , $a_{2}$ , $a_{3}$ 分别为可靠性、材料和运行条件的修正系数; C为基本额定动载荷; P为当量载荷.

经典L-P模型基于轴承所受的内外滚道载荷, 从微观角度分析并计算了轴承疲劳寿命情况, 而ISO计算模型将轴承看作整体进行计算.本文需考虑轴承游隙变化带来的载荷分布变化和对轴承疲劳寿命的影响, 选择经典L-P模型进行改进和分析更为合适.

2 高速列车牵引电机轴承载荷分析

高速列车牵引电机轴承工作在复杂的行车环境下, 且牵引电机频繁启动停止, 高速列车牵引电机轴承受到不同种类的载荷, 电机轴承受载荷的分析结果对于轴承疲劳寿命计算至关重要.正常无偏情况下, 轴承内圈受到轴承内圈和轴伸相互渗透时产生的预紧力、轴伸自身重力以及在轴承转动过程中滚子产生的离心力.而在转子加工制造及安装过程中产生的误差会导致转子偏心, 从而产生电机偏心磁拉力影响轴承受载情况.

2.1 轴承内圈预紧力

牵引电机转子自身重量不能满足轴承所需最小载荷要求, 为保证轴承内圈和转子轴正常咬合, 安装轴承时需要过盈装配, 此时轴承内圈受到一个径向预紧力.根据文献[16], 圆柱滚子轴承的最小径向载荷计算公式如下

$F_{rm} = k_{r} (6 + 4 \times \frac{n}{n_{r}}) {(\frac{d_{m}}{100})}^{2}$ (5)

式中: $F_{rm}$ 为最小径向负荷, kN; $k_{r}$ 为最小负荷系数; $n_{r}$ 为参考转速; $n$ 为轴承实际转速, 单位均为r/min; $d_{m}$ 为轴承平均直径, mm, 由此计算牵引电机轴承内圈所受预紧力.

2.2 轴承滚子离心力

在轴承转动过程中, 轴承滚子会受到惯性离心力, 每个滚子产生的离心力为^[17]

$F_{c} = 3.39 \times 10^{- 11} D_{w}^{2} l D_{pw} n_{m}^{2}$ (6)

式中: $F_{c}$ 是滚子离心力, N; $D_{pw}$ 是轴承节圆直径; $l$ 是滚子长度; $D_{w}$ 是滚动体中心所在直径, 单位均为mm; $n_{m}$ 是滚子的公转速度, r/min.

2.3 电机主轴重力

电机主轴的重力按照电机对应的主轴体积和材料密度计算.

2.4 转子偏心时的单边磁拉力

工程上对于不平衡磁拉力的计算一般采用线性经验公式, 将磁拉力与转子偏心率的关系视为线性关系.而Belmans^{[18, 19]}等提出把气隙磁导展开为Fourier级数的形式, 推导出更精确的不平衡磁拉力解析计算式.单边磁拉力为

$\begin{matrix} F = \sqrt[]{{(\frac{RL' F_{j}^{2} μ_{0}}{2 δ_{0}^{2}} π \frac{r}{δ_{0}} \sin γ)}^{2}} + \sqrt[]{{(\frac{RL' F_{j}^{2} μ_{0}}{2 δ_{0}^{2}} π \frac{r}{δ_{0}} \cos γ)}^{2}} \end{matrix}$ (7)

式中: $μ_{0}$ 为真空磁导率; γ 是转子偏心方向与水平方向的夹角; $F_{j}$ 为转子激磁电流的基波磁动势, V. $δ_{0}$ 是转子不偏心时的气隙长度; r是转子在偏心方向上的位移; R为转子半径; $L'$ 为铁芯长度, mm.

2.5 轴承载荷分布与游隙的关系

高速列车牵引电机运行过程中, 电机轴承因受转子偏心载荷后磨损、润滑油损耗或温度变化等因素, 轴承游隙不断变化, 而轴承游隙变化又将加剧转子偏心和轴承载荷分布不均情况, 使得轴承磨损程度加深.本文基于以上公式, 计算得到滚子轴承在电机转子偏心情况下受到的最终载荷.

以圆柱滚子轴承NU210为例, 构建滚子轴承ANSYS接触仿真模型, 对轴承不同游隙大小时轴承滚子载荷分布情况进行仿真分析.轴承滚道和滚子对应的材料参数及特性:材料种类为GCr15 轴承钢, 密度为7 810 kg· m^-3, 弹性模量为210 GPa, 泊松比为0.29, 抗拉强度为1.617 MPa, 屈服强度为1.458 MPa.

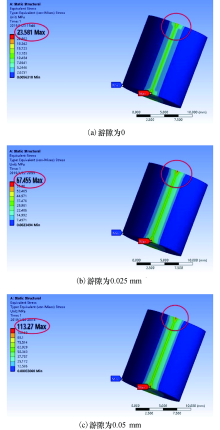
构建圆柱滚子轴承有限元仿真模型, 设定轴承外圈固定, 轴承内、外圈与圆柱滚子设置为接触, 并根据上述轴承受力的具体计算方法, 计算不同游隙下轴承受到的载荷, 并将其施加于轴承内圈.得出轴承不同游隙大小时单个滚子的载荷分布情况见图1, 由图1(a)和图1(b)可以看出, 滚子和滚道接触的两端边缘位置的接触应力比中间位置大, 中间位置的接触应力比较小且均匀, 轴承出现边缘应力集中现象.且由图1(a)、图1(b)和图1(c)对比可以看出, 轴承游隙越大, 边缘应力集中程度越严重.局部的应力过大会使得轴承局部磨损加剧, 寿命下降, 由此得出轴承的游隙变化对轴承载荷分布产生了很大影响, 进而对轴承疲劳寿命产生影响的结论, 传统的疲劳寿命计算方法并未考虑到这一点, 而是基于滚道和滚子接触应力均匀分布的假设, 故有必要研究考虑轴承游隙变化时应力集中现象的改进疲劳寿命计算方法.

	Figure Option View Download New Window
	图1 轴承不同游隙时滚子的载荷分布情况Fig.1 Bearing roller load distribution at different clearance

3 基于Matlab改进疲劳寿命计算

3.1 改进疲劳寿命计算方法

传统的L-P寿命计算模型中将轴承内外圈载荷视为均匀分布情况, 且没有考虑滚动体的疲劳失效, 轴承的整体寿命用轴承内圈和外圈的疲劳寿命加权值得到.而在实际情况下, 轴承游隙在不断变化, 由上述分析得出, 轴承游隙变化时, 电机将受到偏心磁拉力, 偏心磁拉力施加于轴承上将造成轴承载荷增加, 同时出现明显的边缘应力集中现象, 使得轴承滚道和滚子中的载荷分布不同于标准的轴承载荷分布, 故本文为更精确地计算在轴承游隙变化时的疲劳寿命, 采用了改进的L-P计算方法, 即考虑轴承游隙变化时轴承载荷分布偏离标准分布的情况, 对轴承的滚道进行分段, 滚道两端的分段体将承受更大的载荷, 越靠近中间位置, 分段体承受的载荷越小, 与传统L-P方法比较, 还增加考虑了轴承滚动体的疲劳失效, 计算滚道和滚子每段分段体的疲劳寿命, 通过所有分段体的疲劳寿命加权值来计算轴承的疲劳寿命.以下公式取自ISO 281:2007^[20]和ISO/TS16281^[8].

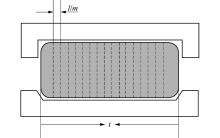
将轴承滚道和滚子平均分成m段, 见图2, 每段为一个宽为l/m的滚子或滚道, 则第k个滚道薄片的基本额定动载荷为

$\begin{array}{l} Q_{cnk} = 552 \frac{{(1 \mp γ)}^{\frac{29}{27}}}{{(1 \pm γ)}^{\frac{1}{4}}} {(\frac{γ}{\cos α})}^{\frac{2}{9}} {D_{w}}^{\frac{29}{27}} {(\frac{l}{m})}^{\frac{7}{9}} Z^{- \frac{1}{4}} \\ n = i, e \end{array}$ (8)

	Figure Option View Download New Window
	图2 轴承滚子切片示意图Fig.2 Bearing roller slice diagram

式中: $γ = \frac{D_{w} \cos α}{D_{pw}}$ ; α 为轴承滚子和滚道的名义接触角; Z为滚子的个数.

第j个滚子的第k个滚子薄片的基本额定动载荷为

$q_{cjk} = q_{cejk} = q_{cijk} = 464 {(1 \mp γ)}^{1.324} {(\frac{l}{m})}^{\frac{7}{9}} {D_{w}}^{\frac{29}{27}}$ (9)

式中: $q_{cijk}$ 与 $q_{cejk}$ 为第j个滚子上第k个薄片分别与内、外滚道第k个薄片接触的基本额定动载荷.

由于边缘应力集中现象, 实际工况下同一个滚子或滚道中每段所受载荷并不完全一样, 在第 $k$ 个内、外滚道薄片上, 滚子与滚道的当量动载荷为

$Q_{ik} = {[\frac{1}{Z} \overset{Z}{\sum_{j = 1}} f_{k} {(Q_{ijk})}^{4}]}^{\frac{1}{4}}$ (10)

$Q_{ek} = {[\frac{1}{Z} \overset{Z}{\sum_{j = 1}} f_{k} {(Q_{ejk})}^{4.5}]}^{\frac{1}{4.5}}$ (11)

其中:

$f_{k} = 1 - [\frac{0.01}{\ln (1985 |\frac{2 k - m - 1}{2 m - 2}|)}]$ (12)

$Q_{ijk} = Q_{ejk} = Q {(\frac{1}{m})}^{\frac{7}{9}}$ (13)

式中: $Q_{ijk}$ 为第j个滚子与内圈滚道上第k个薄片接触的实际载荷; $Q_{ejk}$ 为第j个滚子与外圈滚道上第k个薄片的接触的实际载荷; $f_{k}$ 为滚道第k个薄片上的应力集中系数; Q为轴承单个滚子的当量载荷, 通过上文求得的轴承受到的最终载荷计算得到.

将所有滚道薄片的疲劳寿命进行加权, 得到轴承内外滚道的疲劳寿命为

$\begin{array}{l} L_{i}^{- e} = \overset{m}{\sum_{k = 1}} {[{(\frac{Q_{cik}}{Q_{ik}})}^{4.5}]}^{- e} \\ L_{e}^{- e} = \overset{m}{\sum_{k = 1}} {[{(\frac{Q_{cek}}{Q_{ek}})}^{4.5}]}^{- e} \end{array}$ (14)

式中: $Q_{cik}$ 和 $Q_{cek}$ 分别为内、外滚道薄片的基本额定动载荷; $Q_{ik}$ 和 $Q_{ek}$ 分别为内、外滚道薄片的实际载荷.

早期的L-P疲劳寿命试验数据中, 滚道失效较多, 滚动体的失效数据比较少见.而随着材料性能和套圈制作工艺的提高, 目前生产的轴承中经常出现滚道疲劳失效时滚动体也发生了疲劳失效的情况, 所以原始L-P计算模型中仅考虑滚道失效的计算方法不太适用, 改进的寿命计算模型中同时考虑了滚道与滚子的疲劳失效.滚子薄片分别与内、外滚道薄片接触时的疲劳寿命为

$L_{Rijk} = {(\frac{q_{cijk}}{Q_{ijk}})}^{4}, L_{Rejk} = {(\frac{q_{cejk}}{Q_{ejk}})}^{4.5}$ (15)

上式计算出的是单个滚子的转数, 而轴承的寿命是旋转套圈的转数, 需将滚子的转数转换为旋转套圈的转数.一般来说, 内圈每转一周, 滚子的转数为

$n = \frac{D_{pw}}{2 D_{w}} (1 - γ^{2})$ (16)

将单个滚子薄片的寿命转化为旋转套圈对应的寿命后, 通过式(17)加权计算得到滚子的整体寿命 $L_{r}$

$L_{r}^{- e} = \overset{Z}{\sum_{j = 1}} \overset{m}{\sum_{k = 1}} {(\frac{L_{Rijk}}{n})}^{- e} + \overset{Z}{\sum_{j = 1}} \overset{m}{\sum_{k = 1}} {(\frac{L_{Rejk}}{n})}^{- e}$ (17)

根据计算出的轴承内、外滚道和滚子的疲劳寿命, 加权计算出轴承的整体寿命 $L .$

$\frac{1}{L^{e}} = \frac{1}{L_{i}^{e}} + \frac{1}{L_{e}^{e}} + \frac{1}{L_{r}^{e}}$ (18)

3.2 基于Matlab的疲劳寿命计算

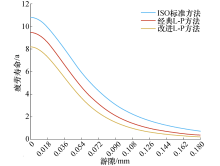基于以上流程和算法, 编制改进疲劳寿命计算模型的Matlab程序, 并与常用的L-P经典模型、ISO计算模型进行实验对比见图3, 以轴承NU210为例.NU210是圆柱滚子轴承, 其基本参数设置为: $d$ =50 mm, $D$ =90 mm, $B$ =20 mm, 基于额定负荷(动态)C=73.5, 静态C_0=69.5, 疲劳负荷极限 $P_{u} = 8.8 kN .$

	Figure Option View Download New Window
	图3 NU210轴承疲劳寿命与轴承游隙的关系Fig.3 Relationship between fatigue life of NU210 bearing and bearing clearance

由图3可以看到, 相较ISO标准方法和经典L-P方法, 本文提出的改进L-P方法计算出的疲劳寿命结果趋于保守, 考虑了轴承游隙增大时造成转子偏心增大, 从而引起转子偏心磁拉力变化影响轴承载荷分布, 出现轴承接触载荷中的边缘应力集中现象, 更符合实际情况.偏心率根据轴承游隙与电机定转子气隙的比值得到, 游隙增长范围较小时(转子偏心1%以内), 轴承疲劳寿命受到的影响不大, 游隙继续增长时, 轴承的疲劳寿命随着游隙变化急剧下降, 在轴承游隙保持0.072 mm(转子偏心4%)以内时, 轴承的疲劳寿命保持在2 a以上, 当轴承游隙增长超过0.09 mm(转子偏心5%)时, 疲劳寿命跌至2 a以下, 当轴承游隙增长至0.108 mm(转子偏心6%)时, 轴承疲劳寿命很小, 已无法满足正常运行所需.

3.3 轴承疲劳寿命计算平台

为了方便快捷地计算不同型号轴承在不同工况下的疲劳寿命, 利用Matlab的GUI界面编程, 编制了高速列车牵引电机滚动轴承疲劳寿命的计算平台, 如图4所示.该平台以牵引电机参数、轴承参数、工况参数为输入, 输出改进疲劳寿命计算模型下的疲劳寿命值.平台主要分为3部分.1)牵引电机参数的存储和读写, 根据输入的游隙参数和电机参数进行轴承整体受力的计算; 2)轴承参数的存储和读写, 根据轴承参数和轴承受力情况, 采用改进疲劳寿命计算模型进行疲劳寿命的计算; 3)寿命修正与可视化界面搭建, 根据用户自定义输入的润滑剂参数、污染等级参数, 对2)计算得到的寿命进行修正, 得到最终疲劳寿命值.将轴承工作游隙值转化为电机转子偏心率, 计算转子不同偏心率下轴承疲劳寿命的情况, 并以寿命曲线的形式表现出来.

	Figure Option View Download New Window
	图4 高速列车牵引电机滚动轴承疲劳寿命计算平台Fig.4 Rolling bearing fatigue life calculation platform for high-speed train traction motor

4 结论

1)牵引电机滚子轴承受载时, 滚子与滚道内部接触将产生边缘应力集中现象, 且随着轴承游隙增长, 边缘应力集中现象不断加剧.采用改进L-P寿命计算法对轴承疲劳寿命进行计算, 考虑了内部载荷边缘应力集中效应以及由于游隙增长导致的电机偏心磁拉力的影响, 更符合牵引电机轴承实际工作情况, 可以获得更为精确的寿命计算结果.

2)轴承游隙增幅在较小范围内, 轴承的疲劳寿命有小幅下降但仍在安全范围内, 当游隙扩大超出一定范围, 轴承疲劳寿命继续下降, 将无法保障列车安全运行.

参考文献

文献列表

[1]	冯磊. 滚动轴承零件表面应力分布对其寿命影响[J]. 机械制造, 2018, 47(4): 10-12. FENG Lei. Effect of surface stress distribution of roll bearing on its life parts[J]. Machine Building & Automation, 2018, 47(4): 10-12. (in Chinese) [本文引用:1]
[2]	闫鑫. 滚动轴承力学特性的有限元分析研究[D]. 武汉: 华中科技大学, 2013. YAN Xin. Analytical research on mechanical properties of rolling bearings based on finite element method[D]. Wuhan: Huazhong University of Science and Technology, 2013. (in Chinese) [本文引用:1]
[3]	张亚军, 王建共. 滚动轴承疲劳寿命理论模型的争比模式评价[J]. 轴承, 2012(6): 33-36. ZHANG Yajun, WANG Jiangong. Evaluation on comparison model of fatigue life theoretical models for rolling bearing[J]. Beaing, 2016(6): 33-36. (in Chinese) [本文引用:1]
[4]	关健. 载荷波动对滚动轴承疲劳寿命影响的研究[D]. 哈尔滨: 哈尔滨工业大学, 2014. GUAN Jian. Study of effects on rolling bearing’s fatigue life considering load fluctuation[D]. Harbin: Harbin Institute of Technology, 2014. (in Chinese) [本文引用:1]
[5]	尚立龙. 风电机组主轴轴承疲劳寿命分析与数值模拟[D]. 北京: 华北电力大学, 2013. SHANG Lilong. Analysis and numerical simulation of fatigue life of main shaft bearing in wind turbine[D]. Beijing: North China Electric Power University, 2013. (in Chinese) [本文引用:2]
[6]	朱亮亮, 林素敏, 吉晓民. 滚动轴承寿命计算方法发展的研究与分析[J]. 哈尔滨轴承, 2014(3): 3-6. ZHU Liangliang, LIN Sumin, JI Xiaomin. Research and analysis of development of life calculation method of rolling bearing[J]. Journal of Harbin Bearing, 2014(3): 3-6. (in Chinese) [本文引用:1]
[7]	鄢建辉, 李兴林, 蒋万里, 等. 轴承疲劳寿命理论的新进展[J]. 轴承, 2005(11): 38-44. YAN Jianhui, LI Xinglin, JIANG Wanli, et al. Progress of fatigue life theory of bearings[J]. Bearing, 2005(11): 38-44. (in Chinese) [本文引用:1]
[8]	查浩, 任尊松, 薛蕊. 高速动车组轴箱轴承累积损伤与疲劳寿命研究[J]. 铁道学报, 2018, 40(10): 30-35. ZHA Hao, REN Zunsong, XUE Rui. Study on cumulative damage and fatigue life of axle box bearings in high-speed EMU[J]. Journal of the China Railway Society, 2018, 40(10): 30-35. (in Chinese) [本文引用:2]
[9]	Rolling bearings-Methods for calculating the modified reference rating life for universally loaded bearings: ISO/TS 16281—2008[S]. Switzerland : ISO copyright office, 2008. [本文引用:1]
[10]	白雪峰, 郭长建, 赵联春. 滚动轴承最佳工作游隙的确定及分析[J]. 轴承, 2013(9): 1-5. BAI Xuefneg, GUO Changjian, ZHAO Lianchun. Determination and analysis of optimum working clearance for rolling bearings[J]. Bearing, 2013(9): 1-5. (in Chinese) [本文引用:1]
[11]	冷钢. 复合工况下高速滚动轴承的寿命和可靠性预测[D]. 哈尔滨: 哈尔滨工业大学, 2012. LENG Gang. Prediction on life and reliability of high speed rolling bearing in complex operating conditions[D]. Harbin: Harbin Institute of Technology, 2012. (in Chinese) [本文引用:1]
[12]	刘德昆. 高速列车轴箱轴承疲劳寿命及可靠性研究[D]. 北京: 北京交通大学, 2017. LIU Dekun. Research on fatigue life and reliability of high-speed train axle box beaing[D]. Beijing: Beijing Jiaotong University, 2017. (in Chinese) [本文引用:1]
[13]	孙春一, 金世哲. 考虑径向游隙的滚动轴承修正额定寿命计算[J]. 润滑与密封, 2012(10): 99-101. SUN Chunyi, JIN Shizhe. Calculation of the rolling bearings adjusted rating life considering radial clearance[J]. Lubrication Engineering, 2012(10): 99-101. (in Chinese) [本文引用:1]
[14]	李震, 商慧玲, 张旭, 等. 高速动车轴箱轴承疲劳寿命计算方法[J]. 铁道学报, 2020, 42(3): 55-62. LI Zhen, SHANG Huiling, ZHANG Xu, et al. Fatigue life calculation method for axle box bearing of high-speed train[J]. Journal of the China Railway Society, 2020, 42(3): 55-62. (in Chinese) [本文引用:1]
[15]	徐鹤琴, 汪久根, 王庆九. 滚动轴承疲劳失效过程与寿命模型的研究[J]. 轴承, 2016(4): 57-62. XU Heqin, WANG Jiugen, WANG Qingjiu. Study on life model and fatigue failure process for rolling bearing[J]. Bearing, 2016(4): 57-62. (in Chinese) [本文引用:1]
[16]	SKF. SKF轴承综合型录[M]. 上海: 上海科学技术文献出版社, 2004. SKF. SKF Bearing comprehensive catalogue[M]. Shanghai: Shanghai Science and Technology Literature Publishing House, 2004. (in Chinese) [本文引用:1]
[17]	徐鹤琴. 滚动轴承内部载荷序列分析与寿命计算[D]. 杭州: 浙江大学, 2017. XU Heqin. Internal load sequence analysis and life calculation of rolling bearing[D]. Hangzhou: Zhejiang University, 2017. (in Chinese) [本文引用:1]
[18]	BELMANS R, VANDENPUT A, GEYSEN W. Calculation of the flux density and the unbalanced pull in two pole induction machines[J]. Archiv fur Elektrotechnik, 1987, 70(1): 151-161. [本文引用:1]
[19]	BELMANS R, VANDENPUT A, GEYSEN W. Influence of unbalanced magnetic pull on the radial stability of flexible-shaft induction machines[J]. IEEE Proceedings B-Electric Power Applications, 1987, 134(2): 101-109. [本文引用:1]
[20]	Rolling bearings-dynamic load ratings and rating life: ISO 281—2007[S]. Switzerland : ISO copyright office, 2007. [本文引用:1]

2018

0.0

... 在高速列车动力系统中,滚动轴承作为重要的旋转机械零部件起到了至关重要的作用^[1],而高速列车运行环境复杂且速度较高,因此高速列车牵引电机轴承也易损坏 ...

2013

0.0

... 滚动轴承工作环境复杂,由于材料、安装使用不当等原因,会出现多种形式的失效^[2],其中滚动接触疲劳最为典型^[3] ...

0.0

... 滚动轴承工作环境复杂,由于材料、安装使用不当等原因,会出现多种形式的失效^[2],其中滚动接触疲劳最为典型^[3] ...

2014

0.0

... 早期,基于大量滚动轴承的疲劳试验可以预测轴承的寿命^[4],理论和实践结果证明轴承的疲劳寿命服从Weibull分布,而后Lundberg和Palmgren基于Weibull理论,利用Hertz弹性接触理论计算出滚动承受的最大接触应力,再结合额定动载荷理论计算出轴承疲劳寿命,创立了L-P寿命计算模型^[5] ...

2013

0.0

... 1 经典L-P模型经典L-P模型^[5]假设位于表面下某处深度的最大正交剪应力导致了裂纹产生,进而主导了轴承失效 ...

0.0

... 1962年,ISO将原始的L-P寿命公式列为推荐标准ISO/R281/1-1962^[6] ...

0.0

... 而后,文献[7]说明了应用材料疲劳破坏极限与离散有限元体积法修正了L-P理论,简称为 I-H 理论 ...

2018

0.0

... 文献[8]考虑了轴承内表面法向力和切向力的情况下,综合轴承寿命实验的研究成果进一步充实了L-P理论 ...

... 以下公式取自ISO 281:2007^[20]和ISO/TS16281^[8] ...

2008

0.0

... ISO/TS16281^[9]中给出了 αISO的计算方法, αISO是一个与环境污染系数、黏度比、静态额定载荷和动态载荷有关的寿命修正系数,用它对基本额定疲劳寿命修正后能得到更加符合现场环境和轴承状态的疲劳寿命估计 ...

0.0

... 轴承在实际运行过程中,可能会出现不对中、游隙变化等情况,滚动轴承中的径向游隙对轴承疲劳寿命有重大影响作用^[10],文献[11]在L-P理论的基础上,研究了过盈配合、初始游隙、弯矩、温度及残余应力对疲劳寿命的影响,建立了滚子轴承疲劳寿命的修正计算模型 ...

2012

0.0

2017

0.0

... 文献[12]分别使用有限元方法、Harris方法和静力学方法分析了游隙对轴承内部载荷分布情况的影响,发现游隙变化时,载荷分布及最大接触载荷受到影响,游隙增大时,承载滚子数减少,最大接触载荷增大 ...

0.0

... 文献[13]将径向游隙看作最小油膜厚度,添加寿命润滑修正系数进行滚动轴承寿命的计算 ...

2020

0.0

... 文献[14]对滚动轴承不同游隙时轴承的载荷分布和疲劳寿命情况做了很多研究,发现轴承游隙变化确实会对疲劳寿命产生影响 ...

0.0

... 2 ISO计算模型ISO对基于L-P理论的寿命计算进行修正,加入可靠性、材料和运行条件这3个修正系数得到修正疲劳寿命^[15],计算公式如下 ...

2004

0.0

... 根据文献[16],圆柱滚子轴承的最小径向载荷计算公式如下 ...

2017

0.0

... 2 轴承滚子离心力在轴承转动过程中,轴承滚子会受到惯性离心力,每个滚子产生的离心力为^[17] ...

1987

0.0

... 而Belmans^[18,19]等提出把气隙磁导展开为Fourier级数的形式,推导出更精确的不平衡磁拉力解析计算式 ...

1987

0.0

... 而Belmans^[18,19]等提出把气隙磁导展开为Fourier级数的形式,推导出更精确的不平衡磁拉力解析计算式 ...

2007

0.0

... 以下公式取自ISO 281:2007^[20]和ISO/TS16281^[8] ...