考虑死区时间的直线感应电机参数静止自整定方法

引用本文

吕刚, 杨琛, 罗志昆. 考虑死区时间的直线感应电机参数静止自整定方法[J]. 北京交通大学学报, 2020,44(1): 91-97.
LYU Gang, YANG Chen, LUO Zhikun. Parameter static self-tuning method of linear induction motor considering dead-time[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2020,44(1): 91-97.
Doi:10.11860/j.issn.1673-0291.20180166 复制到剪切板

Permissions

北京交通大学学报编辑部所有

考虑死区时间的直线感应电机参数静止自整定方法

吕刚, 杨琛, 罗志昆

北京交通大学电气工程学院,北京 100044

第一作者:吕刚(1976—),男,河南焦作人,教授,博士,博士生导师.研究方向为轨道交通大功率直线电机及其驱动系统、新型高速磁悬浮及电磁推进技术.email:ganglv@bjtu.edu.cn.

收稿日期: 2018-11-29

基金: 国家自然科学基金(51377009,51777009)

摘要

针对直线感应电机初级和次级漏感不相等的特点,对直线感应电机静止状态下的参数辨识方法进行研究.首先,分别针对死区时间为0、1、2、3和4 μs的情况进行场路联合有限元法仿真.利用PWM逆变器依次向直线感应电机中通入单相直流电压、单相交流高频电压和单相交流低频电压来获得等效电路中的各个参数.然后,将不同死区时间下的辨识结果与实际值进行比较,并进行误差对比,讨论不同的死区时间对辨识精度的影响.最后,分别分析死区效应对初级电阻及漏感、互感、次级电阻及漏感的辨识结果产生的影响.结果表明:在考虑到直线感应电机的初、次级漏感不相等的情况下提出的基于PWM逆变器的静止状态下参数辨识方法,辨识结果比较精确,验证了方法的正确性,死区效应的存在对直线电机各个参数的辨识结果均产生影响.

关键词: 直线感应电机; 参数辨识; 死区效应; 场路联合有限元法仿真

中图分类号:TM359.4 文献标志码:A 文章编号:1673-0291(2020)01-0091-07

Parameter static self-tuning method of linear induction motor considering dead-time

LYU Gang, YANG Chen, LUO Zhikun

School of Electrical Engineering, Beijing Jiaotong University, Beijing 100044, China

Fund:National Natural Science Foundation of China (51377009,51777009)

Abstract

In view of the fact that the primary and secondary leakage inductances of the linear induction motor are not equal, the parameter identification methods of the linear induction motor in static state is studied. Firstly, the field-circuit coupling finite element method simulation is performed under the dead time of 0, 1, 2, 3 and 4 μs. The PWM inverter is used to input single-phase DC voltage, single-phase high-frequency AC voltage, and single-phase low-frequency AC voltage into the linear induction motor sequentially to obtain parameters of the equivalent circuit. Then, the identification results under different dead time are compared with the actual values, and error comparison is conducted. Therefore the impact of different dead time on the accuracy of identification is discussed.Finally, the effect of the dead zone effect on the identification results of primary resistance, leakage inductance, mutual inductance, secondary resistance and leakage inductance are analyzed separately. The results show that the consequence of the parameter identification method based on PWM inverter are more accurate when considering the fact that primary and secondary leakage inductance of linear induction motor are not equal,and the correctness of method is verified. The dead zone effect can impact the parameter identification results of linear motor.

Keyword: linear induction motor; parameter identification; dead zone effect; field-circuit coupling finite element method simulation

文章图片

电机参数的精确与否是影响电机控制精度的关键因素.与传统的旋转感应电机不同, 通常情况下直线感应电机(Linear Induction Motor, LIM)的机械气隙相对较大, 因此其励磁电感比同容量的旋转感应电机小很多^[1].并且直线感应电机的初级绕组嵌套在槽内, 次级部分则是由整块的铝板和次级铁轭压制而成, 没有与旋转感应电机的鼠笼式转子导条和短路环相似的结构, 所以直线感应电机的初级漏感比次级漏感要大得多^[2].因而, 采取传统旋转感应电机的参数辨识方法对直线感应电机的参数进行辨识, 辨识误差较大, 无法满足辨识精度的要求.

文献[3]提出的参数辨识方法是基于变频器本身来实现的, 不需要额外添加设备对电机进行机械堵转, 但是该方法只适用于定子漏感和转子漏感相同的传统感应电机, 对于初、次级漏感不相等的直线感应电机来说, 会导致辨识精度无法满足要求.文献[4]提出了一种根据感应电机铭牌上的数据和稳态模型获得电机稳定状态及启动时的参数.但是主要针对大型火力发电厂的泵电动机, 以及实际的紧急启动案例研究有效, 且要求现场操作人员具有较高的专业技能.文献[5, 6]通过空载实验和堵转实验获取电机的参数, 但是空载实验需要去除次级铝板.而短初级直线感应电机的初级悬挂在车上, 次级铺设在地面上作为轨道, 在通电后还会形生法向力作用于电机, 产生运行阻力, 导致空载实验在实际情况中实施困难^[7].文献[8]利用静态频率响应测试从感应电机的二阶传递函数导出等效电路模型, 但是这种方法需要用到频率响应分析仪和功率放大器.文献[9]采用PWM逆变器进行参数辨识, 采用向电机中通入直流的实验方法得到电机的初级参数, 通过从整个电路的等效电感中求解三阶多项式得出互感, 从而可以分别求出初级和次级漏感.这种方法利用PWM逆变器输出的d、q两轴为0代替堵转实验, 虽然考虑到了次级漏感与初级漏感不相等的问题, 但是没有讨论死区效应对参数辨识的影响.

本文作者针对目前直线感应电机通常采用变频器进行驱动控制的现状, 结合三相电压型逆变电路供电的特点, 在考虑到直线电机初、次级漏感不相等特性的情况下, 提出了一种基于PWM逆变器对直线感应电机等效电路进行参数辨识的方法, 不需要添加额外的设备对电机进行机械堵转, 而是添加一段参数辨识的程序, 就可以直接将辨识结果传给电机的控制程序.另外, 由于直线感应电机存在边端效应, 以及轨道长度的有限性和运动位置不重复性, 旋转感应电机的空载离线参数测量和在线辨识方法对于直线感应电机通常是不太可行的^[10].因此, 通过向电机施加单相激励, 即可以使电机在保持静止的状态下获取电机的参数.为了使辨识过程更接近于工程实际, 采用Simplore与Maxwell软件在不同死区时间的条件下进行场路联合有限元仿真, 讨论死区效应对参数辨识精度的影响.

1 参数辨识方法

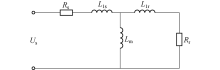
直线感应电机处于静止状态下的T型等效电路如图1所示.其中 $R_{s}$ 为初级电阻, L_1s 为初级漏感, L_m 为互感, L_1r 为折算到初级的次级漏感, R_r 为折算到初级的次级电阻, U_s为初级端电压.

	Figure Option View Download New Window
	图1 直线感应电机的T型等效电路Fig.1 T-equivalent circuit of linear induction motor

1.1 直流实验

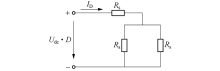
当给直线电机通入直流电压时, 电感相当于短路, 电压完全施加在初级电阻两侧, 因此此时的等效电路中只需要考虑初级电阻, 如图2所示, 图中U_dc 为通入的直流电压, D为降压斩波的占空比, I_D 为通入直流电压后相电流的平均值.由于初级电阻一般阻值较小, 为了防止施加到电机上的电压过大, 需要进行降压斩波.同时, 逆变器开关管的饱和压降和死区时间会对初级电阻辨识结果产生较大的影响, 为了减少辨识误差, 给直线电机通入两次不同的直流电压, 用得到的电压、电流的斜率作为 $R_{s}$ 的估算值.因此, 初级电阻的估算值为

$R_{s} = \frac{2}{3} \frac{D_{1} U_{dc 1} - D_{2} U_{dc 2}}{I_{D 1} - I_{D 2}}$ (1)

式中: $U_{dc 1}$ 和 $U_{dc 2}$ 分别为通入的两次不同的直流电压; D₁ 和D₂ 分别为两次降压斩波的占空比; I_D1 和I_D2分别是通入两次不同的直流电压所得到的电流.

	Figure Option View Download New Window
	图2 通入直流电压的T型等效电路Fig.2 T-equivalent circuit when inputting DC voltage

1.2 交流高频实验

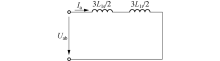
当向直线电机通入单相交流高频电压时, 励磁支路感抗远远大于初、次级漏抗, 从而使得励磁支路流过的电流很少, 可以忽略, 同时, 初、次级电阻也远小于初、次级漏抗, 初、次级电阻上的电压降很小, 也可以忽略.因此, 通入单相交流高频电压时直线感应电机的等效电路由初级漏感和次级漏感串联而成, 如图3所示, $U_{ab}$ 为初级A、B两相绕组之间的电压, $I_{a}$ 为A相电流.

	Figure Option View Download New Window
	图3 通入交流高频电压的T型等效电路Fig.3 T-equivalent circuit when inputting high-frequency AC voltage

通过测量U_ab 和I_a, 可以得到初级漏感与次级漏感之和c.因此, c的估算值为

$c = L_{1 s} + L_{1 r} = \frac{2}{3} \frac{U_{ab}}{ω_{1} I_{a}}$ (2)

$ω_{1} = 2 π f_{1}$ (3)

式中: $ω_{1}$ 为所通入高频电压的角频率; $f_{1}$ 为所通入高频电压的频率.

1.3 交流低频实验

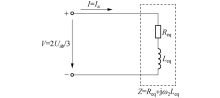
当向直线感应电机施加交流低频电压时, 对等效电路进行简化, 简化后的等效电路如图4所示.

	Figure Option View Download New Window
	图4 通入交流低频电压的T型等效电路Fig.4 T-equivalent circuit when inputting low-frequency AC voltage

图4中, Z是等效阻抗; V是加在等效阻抗上的电压; I是流过等效阻抗的电流; 等效电阻R_eq 、电感L_eq分别表示为

$R_{eq} = \frac{V}{I} \cos φ = R_{s} + \frac{ω_{2} {L^{2}}_{m} R_{r}}{{R^{2}}_{r} + ω_{2}^{2} L_{r}^{2}}$ (4)

$L_{eq} = \frac{V}{I} \sin φ = L_{1 s} + \frac{L_{m} ({R^{2}}_{r} + ω_{2}^{2} L_{r} L_{1 r})}{{R^{2}}_{r} + ω_{2}^{2} L_{r}^{2}}$ (5)

式中: $ω_{2}$ 为所通入低频电压的角频率; 次级电感 $L_{r} = L_{1 r} + L_{m} . 令 R_{eq} - R_{s} = b, L_{r} / L_{m} = k, L_{eq} - c = m, k - 2 = n$ , 通过推导可得, 互感的估算值为

$\begin{array}{l} L_{m} = \frac{- (m + 2 kmn)}{2 (n + k n^{2})} \pm \\ \frac{\sqrt[]{{(m + 2 kmn)}^{2} - 4 k (n + k n^{2}) (m^{2} + \frac{b^{2}}{ω_{2}^{2}})}}{2 (n + k n^{2})} \end{array}$ (6)

次级漏感为

$L_{1 r} = (k - 1) L_{m}$ (7)

初级漏感为

$L_{1 s} = c - L_{1 r}$ (8)

次级电阻为

$R_{r} = \frac{(ω_{2} L_{m})^{2} \pm \sqrt[]{(ω_{2} L_{m})^{4} - (2 ω_{2} L_{r} {b)}^{2}}}{2 b}$ (9)

其中根据经验可得^[11], $1 / k$ 的值约为0.9~0.95, 对于旋转感应电机取0.95, 对于直线感应电机取0.92.

1.4 死区效应分析

理想情况下, 逆变电路上、下桥臂的开关管不会同时导通或关断, 即开通和关断在控制信号发出后动作没有延时.但是在实际情况中, 功率开关管的导通和关断不可能瞬时完成.而由于开关器件的导通时间一般比关断时间长, 导致上、下桥臂开关管同时导通, 造成逆变失败或器件被烧毁^[12].因此要将开关管的触发时间延迟一段时间, 这段延时即为死区时间 $T_{e},$ 确保上组器件可靠关断后再开通下组器件, 使换流过程顺利完成.

由文献[13]可知, 由死区造成的误差电压的一般表达式为

$U_{e z} = - sign (i_{z}) U_{dc} T_{e z} / T_{s}$ (10)

$\{\begin{array}{l} sign (i_{z}) = 1 \\ sign (i_{z}) = - 1 \end{array} \begin{array}{l} i_{z} > 0 \\ i_{z} < 0 \end{array}$ (11)

式中: $z$ =A, B, C; $U_{e z}$ 为A、B、C三相的死区误差电压; $i_{z}$ 为逆变器相电流; $T_{e z}$ 为死区时间; $T_{s}$ 为PWM周期.

根据式(10)、(11)可知, 死区时间将造成与电流方向相反的误差电压.把逆变器给定电压 $U_{zref}$ 改写成矢量形式

$U_{zref} = Re (U_{zref}) + jIm (U_{zref})$ (12)

在考虑死区电压影响后, 桥臂实际输出电压为

$U_{zact} = Re (U_{zref}) - U_{ez} + jIm (U_{zref})$ (13)

由式(13)可知输出电压矢量的虚部不受死区的干扰, 由每个桥臂上死区造成的误差电压幅值不变且只与电流方向有关.

2 场路联合有限元仿真

为了准确地辨识直线感应电机的参数, 考虑到直线感应电机初、次级漏感不相等和边端效应的影响, 以及死区效应对参数辨识精度的影响, 采用场路联合有限元仿真, 在Ansys Maxwell中搭建单边直线感应电机的3D模型, 在Simplore中搭建PWM逆变电路, 来控制施加给直线感应电机的激励^[14].其中, 直线感应电机的主要参数如表1所示.由于在PWM控制中死区时间通常设置为1~4 μ s^[15], 因此将死区时间 $T_{e}$ 分别设置为0、1、2、3、4 μ s, 讨论不同的死区时间对参数辨识精度的影响.

表1 直线感应电机主要参数 Tab.1 Main parameters of linear induction motor

2.1 单相直流实验

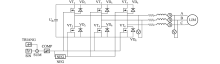
直流实验的场路耦合有限元模型如图5所示.在图5中, VT₁~VT₆为三相桥式逆变电路的6个IGBT开关管, VD₁~VD₆为并联的反馈二极管, VT₄和VT₆始终保持导通, VT₂、VT₃和VT₅始终保持关断, VT₁则通过周期 $T_{s}$ =0.02 s的方波信号来控制导通与关断, 通过改变驱动信号的占空比即可以调整施加给电机的直流电压的幅值.

	Figure Option View Download New Window
	图5 直流实验的场路耦合有限元模型Fig.5 Field-circuit coupling finite element method model of AC circuit experiment

由于占空比的增大, 会使得初级电流增大, 为了保证在实验过程中所选择的占空比可以使得电流不至于过大, 对占空比为5%~50%情况下的初级电流值 $I_{D}$ 进行研究, 结果如表2所示.

表2 不同占空比下的初级电流平均值 Tab.2 Mean value of primary current with different duty ratio

占空比/%	$I_{D}$ /A	占空比/%	$I_{D}$ /A
5	1.580	30	9.503
10	3.151	35	11.055
15	4.732	40	12.643
20	6.328	45	14.353
25	7.899	50	15.764

表2 不同占空比下的初级电流平均值 Tab.2 Mean value of primary current with different duty ratio

根据表1给出的电机参数计算电机额定电流为7.22 A.因此, 为了保证流过电机的电流不超过电机的额定电流, 所选占空比不大于20%.

2.2 单相交流实验

交流实验场路耦合有限元模型如图6所示.其中, VT₄和VT₆保持同步导通或关断, VT₃和VT₅保持同步或关断, 此时B、C相相当于并联, 直线电机中施加的电压等效为单相电压.

	Figure Option View Download New Window
	图6 交流实验的场路耦合有限元模型Fig.6 Field-circuit coupling finite element method model of AC circuit experiment

当进行高频实验时, 所通入电压频率 $f_{1}$ =500 Hz, 周期 $T_{s 1}$ =0.002 s, 仿真得到的电压、电流如图7、图8所示.

	Figure Option View Download New Window
	图7 高频交流仿真实验中的初级电压Fig.7 Primary voltage in high-frequency AC simulation

	Figure Option View Download New Window
	图8 高频交流仿真实验中的初级电流Fig.8 Primary current in high-frequency AC simulation

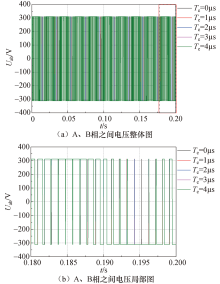
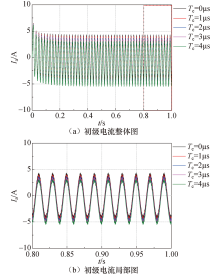
从图7可知, 由于死区时间的存在, 产生的PMW脉冲宽度发生了变化.在一个周期内, 正弦波正半波对应的脉宽减小, 负半波对应的脉宽增大, PWM波形发生畸变, 稍稍偏离正弦波.从图8可知, 死区效应导致初级电流减小, 且稳定速度减慢.

对所得的电压、电流进行傅里叶分析, 结果如表3所示.可以看出, 死区时间的存在导致电压 $U_{ab}$ 和电流 $I_{a}$ 的幅值均减小, 且死区时间越长, 减小的越明显.

表3 高频交流仿真实验中傅里叶分析结果 Tab.3 Fourier analysis results in high-frequency AC simulation

死区时间 $T_{e}$ /μ s	电压 $U_{ab}$ /V	电流 $I_{a}$ /A
0	302.504	0.403
1	299.651	0.400
2	290.424	0.388
3	278.202	0.372
4	261.55	0.350

表3 高频交流仿真实验中傅里叶分析结果 Tab.3 Fourier analysis results in high-frequency AC simulation

进行低频实验时, 所选频率 $f_{2}$ =50 Hz, $T_{s 2}$ =0.02 s, 对所得电压、电流进行傅里叶分析, 结果如表4所示.实验仿真得到的电压、电流如图9、10所示.

表4 低频交流仿真实验中傅里叶分析结果 Tab.4 Fourier analysis results in low-frequency AC simulation

死区时间 $T_{e}$ /μ s	$U_{ab}$ /V	$I_{a}$ /A
0	311.265	4.028
1	310.965	4.027
2	310.655	4.023
3	310.344	4.019
4	309.731	4.011

表4 低频交流仿真实验中傅里叶分析结果 Tab.4 Fourier analysis results in low-frequency AC simulation

	Figure Option View Download New Window
	图9 低频交流仿真实验中的初级电压Fig.9 Primary voltage in low-frequency AC simulation

	Figure Option View Download New Window
	图10 低频交流仿真实验中的初级电流Fig.10 Primary current in low-frequency AC simulation

由表4可知, 由于f₁ 远大于f₂, 可得T_s1 远小于T_s2, 因此低频实验中电压、电流的仿真结果趋势同高频实验一致, 但是死区时间对低频实验的影响远小于高频实验.

3 结果分析

直流实验中, 将表2中的电流有效值代入式(1)进行计算, 得到不同死区条件下初级电阻R_s 的估算值; 高频交流实验中, 将表3中电压、电流的幅值代入式(2), 得到各个死区时间下初级漏感和次级漏感之和c的估算值; 在低频交流实验中, 将表4中电压、电流的幅值代入式(4)、式(5)得到等效电阻R_eq 和等效电感L_eq, 再根据式(6)~ 式(9)计算得到互感L_m 、次级漏感L_1r 、初级漏感L_1s 和次级电阻R_r的估算值.因此, 电机实际参数与辨识结果如表5所示.

表5 辨识结果对比 Tab.5 Comparison of identification results

实验方法	参数	实际值	$T_{e}$ /μ s
实验方法	参数	实际值	0	1	2	3	4
直流实验	$R_{s}$ /Ω	6.56	6.58	6.58	6.58	6.58	6.58
高频实验	$c$ /mH	160.00	159.14	158.97	158.84	158.70	158.58
低频实验	$L_{1 s}$ /mH	136.52	136.61	136.95	137.59	137.94	138.65
	$L_{m}$ /mH	269.91	261.24	253.07	245.79	238.59	229.13
	$L_{1 r}$ /mH	23.48	22.53	22.02	21.38	20.76	19.93
	$R_{r}$ /Ω	6.52	6.20	6.10	6.02	5.94	5.83

表5 辨识结果对比 Tab.5 Comparison of identification results

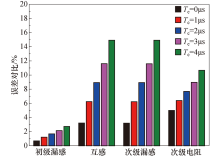
从表5中可知, 当 $T_{e}$ =0 μ s, 即不考虑死区时间时, 与电机实际参数值进行比较, 初级电阻和初级漏感辨识结果偏大, 互感、次级漏感和次级电阻辨识结果偏小.直流实验中, 死区时间对初级电阻的辨识结果没有影响, 这是由于直流实验中利用电压、电流斜率进行计算, 消除了死区效应的影响.在高频交流实验中, 死区效应的影响使得初级漏感与次级漏感之和 $c$ 的辨识结果减小.在低频交流实验中, 死区时间的存在使得初级漏感辨识结果增大, 互感、次级漏感和次级电阻的辨识结果减小.

各个参数辨识结果的误差对比如图11所示.

	Figure Option View Download New Window
	图11 各个参数辨识结果误差对比Fig.11 Comparison of identification result error

从图11可知, 所有参数的辨识结果误差都在15%以内, 基本满足辨识精度的要求.但是死区效应的存在使得辨识误差增大, 且死区时间越大, 误差越大.当死区时间设置在2 μ s以内时, 所有参数的辨识误差可以控制在10%以内.另外, 死区效应对互感、次级电阻和次级漏感的辨识影响较大, 对初级漏感辨识的结果影响相对较小.

4 结论

1)在考虑直线感应电机初级漏感和次级漏感不相等的情况下, 提出了一种利用PWM逆变器对直线感应电机进行单相实验, 从而辨识出电机等效电路参数的方法.

2)利用Ansys Maxwell搭建直线感应电机的三维有限元模型, 并通过Simplore搭建电压型逆变电路为电机提供所需要的单相直流电压、单相高频交流电压和单相低频交流电压, 在设置不同死区的条件下进行联合仿真, 说明死区效应使得电压波形产生畸变, 电压和电流幅值均减小.仿真过程中考虑到了PWM逆变电路的死区效应及直线感应电机的边端效应, 仿真过程更接近于实际应用.

3)将辨识结果与电机实际参数进行对比及误差分析, 可以得到死区效应使得初级漏感辨识结果增大, 互感、次级漏感和次级电阻辨识结果减小, 对初级电阻辨识则不产生影响.死区时间越大, 参数辨识的误差越大.另外, 死区效应对初级漏感的辨识影响较小, 而对互感和次级参数的辨识影响较大.

4)辨识结果验证了本文方法的正确性.同时, 当死区时间设置在2 μ s以内时, 辨识精度较高.所提出的参数辨识方法实施简单并且不需要使用额外的测量仪器, 在工业和交通领域具有较高的应用价值.

参考文献

文献列表

[1]	何晋伟, 史黎明. 一种基于静态特性的直线感应电机参数辨识方法[J]. 电工电能新技术, 2009, 28(4): 50-53. HE Jinwei, SHI Liming. An identification method for linear induction motor parameter based on static characteristics[J]. Advanced Technology of Electrical Engineering and Energy, 2009, 28(4): 50-53. (in Chinese) [本文引用:1]
[2]	ZENG D H, LYU G, ZHOU T. Equivalent circuits for single-sided linear induction motors with asymmetric cap secondary for linear transit[J]. IEEE Transactions on Energy Conversion, 2018, 33(4): 1729-1738. [本文引用:1]
[3]	杨坤, 赵金. 基于变频器的感应电机离线参数辨识策略[J]. 微电机, 2013, 46(9): 49-53. YANG Kun, ZHAO Jin. Off-line parameter identification strategy for induction motor based on inverter[J]. Micromotors, 2013, 46(9): 49-53. (in Chinese) [本文引用:1]
[4]	LINDENMEYER D, DOMMEL H W, MOSHREF A, et al. An induction motor parameter estimation method[J]. International Journal of Electrical Power & Energy Systems, 2001, 23(4): 251-262. [本文引用:1]
[5]	GIERAS J F. Linear induction derives[M]. Oxford: Clarendon Press, 1994. [本文引用:1]
[6]	徐伟, 孙广生, 李耀华, 等. 一种新型的直线异步电机参数测量方案[J]. 电工技术学报, 2007, 22(6): 54-58. XU Wei, SUN Guangsheng, LI Yaohua, et al. A new parameter measurement scheme for single linear induction motors[J]. Transactions of China Electrotechnical Society, 2007, 22(6): 54-58. (in Chinese) [本文引用:1]
[7]	吕刚, 邢程程, 周桐. 静止状态下直线感应电机的参数辨识方法[J]. 北京交通大学学报, 2017, 41(5): 120-125. LYU Gang, XING Chengcheng, ZHOU Tong. Parameter estimation of linear induction motor at stand still[J]. Journal of Beijing Jiaotong University, 2017, 41(5): 120-125. (in Chinese) [本文引用:1]
[8]	WILLIS J R, BROCK G J, EDMONDS J S. Derivation of induction motor models from stand still frequency response tests[J]. IEEE Power Engineering Review, 1989, 9(12): 37-38. [本文引用:1]
[9]	KANG G, KIM J, NAM K. Parameter estimation scheme for low-speed linear induction motors having different leakage inductances[J]. IEEE Transactions on Industrial Electronics, 2003, 50(4): 708-716. [本文引用:1]
[10]	吕刚, 刘素阔, 周桐. 直线感应电机的次级阻抗角计算及对涡流损耗的影响[J]. 北京交通大学学报, 2016, 40(5): 76-80. LYU Gang, LIU Sukuo, ZHOU Tong. Calculation of the secondary impedance angle of linear induction motor and its influence on eddy current losses[J]. Journal of Beijing Jiaotong University, 2016, 40(5): 76-80. (in Chinese) [本文引用:1]
[11]	张文雅, 刘少克. 基于PWM逆变器的直线感应电机参数辨识方法[J]. 电气传动自动化, 2005, 27(6): 25-27. ZHANG Wenya, LIU Shaoke. Parameter estimation of a linear induction motor based on PWM inverter[J]. Electrical Drive Automation, 2005, 27(6): 25-27. (in Chinese) [本文引用:1]
[12]	陈伟, 邹云屏, 耿攀. 三相PWM整流器的死区效应分析及补偿方法[J]. 高电压技术, 2009, 35(5): 1156-1163. CHEN Wei, ZOU Yunping, GENG Pan. Analysis and compensation of dead-time effects in three-phase PWM rectifiers[J]. High Voltage Engineering, 2009, 35(5): 1156-1163. (in Chinese) [本文引用:1]
[13]	刘鹏, 吴文进, 苏建徽. 一种异步电动机静止状态下参数辨识的改进方法[J]. 电工技术学报, 2015, 30(5): 42-48. LIU Peng, WU Wenjin, SU Jianhui. An improved parameters estimation algorithm for induction motor in the stand still state[J]. Transactions of China Electrotechnical Society, 2015, 30(5): 42-48. (in Chinese) [本文引用:1]
[14]	林庸, 吕刚, 周桐, 等. 初级横向偏移时直线电机的特性分析[J]. 北京交通大学学报, 2018, 42(6): 104-110. LIN Yong, LYU Gang, ZHOU Tong, et al. Analysis of characteristics of linear motor with primary lateral offset[J]. Journal of Beijing Jiaotong University, 2018, 42(6): 104-110. (in Chinese) [本文引用:1]
[15]	JEONG S G, PARK M H. The analysis and compensation of dead-time effects in PWM inverters[J]. IEEE Transactions on Industrial Electronics, 1991, 38(2): 108-114. [本文引用:1]

2009

0.0

... 与传统的旋转感应电机不同,通常情况下直线感应电机(Linear Induction Motor,LIM)的机械气隙相对较大,因此其励磁电感比同容量的旋转感应电机小很多^[1] ...

2018

0.0

... 并且直线感应电机的初级绕组嵌套在槽内,次级部分则是由整块的铝板和次级铁轭压制而成,没有与旋转感应电机的鼠笼式转子导条和短路环相似的结构,所以直线感应电机的初级漏感比次级漏感要大得多^[2] ...

2013

0.0

... 文献[3]提出的参数辨识方法是基于变频器本身来实现的,不需要额外添加设备对电机进行机械堵转,但是该方法只适用于定子漏感和转子漏感相同的传统感应电机,对于初、次级漏感不相等的直线感应电机来说,会导致辨识精度无法满足要求 ...

2001

0.0

... 文献[4]提出了一种根据感应电机铭牌上的数据和稳态模型获得电机稳定状态及启动时的参数 ...

1994

0.0

... 文献[5,6]通过空载实验和堵转实验获取电机的参数,但是空载实验需要去除次级铝板 ...

2007

0.0

... 文献[5,6]通过空载实验和堵转实验获取电机的参数,但是空载实验需要去除次级铝板 ...

2017

0.0

... 而短初级直线感应电机的初级悬挂在车上,次级铺设在地面上作为轨道,在通电后还会形生法向力作用于电机,产生运行阻力,导致空载实验在实际情况中实施困难^[7] ...

1989

0.0

... 文献[8]利用静态频率响应测试从感应电机的二阶传递函数导出等效电路模型,但是这种方法需要用到频率响应分析仪和功率放大器 ...

2003

0.0

... 文献[9]采用PWM逆变器进行参数辨识,采用向电机中通入直流的实验方法得到电机的初级参数,通过从整个电路的等效电感中求解三阶多项式得出互感,从而可以分别求出初级和次级漏感 ...

2016

0.0

... 另外,由于直线感应电机存在边端效应,以及轨道长度的有限性和运动位置不重复性,旋转感应电机的空载离线参数测量和在线辨识方法对于直线感应电机通常是不太可行的^[10] ...

2005

0.0

... 其中根据经验可得^[11], 1/k的值约为0 ...

2009

0.0

... 而由于开关器件的导通时间一般比关断时间长,导致上、下桥臂开关管同时导通,造成逆变失败或器件被烧毁^[12] ...

2015

0.0

刘鹏, 吴文进, 苏建徽. 一种异步电动机静止状态下参数辨识的改进方法[J]. 电工技术学报, 2015, 30(5): 42-48.

LIU

Peng

, WU

Wenjin

, SU

Jianhui

. An improved parameters estimation algorithm for induction motor in the stand still state[J]. Transactions of China Electrotechnical Society, 2015, 30(5): 42-48. (in Chinese)

In order to obtain the accurate induction motor (IM) parameters in the standstill state,an improved algorithm for parameter identification based on the asymmetric T type circuit is proposed.It is proved that only the active component of the output voltage is affected by the inverter dead time.Based on it,the accuracy of IM parameters estimation is improved through the adaptive compensation for the inverter dead time.The rotor resistor is identified through injecting two single phase alternating currents with identical slip frequency,and different amplitudes,proposing the adaptive algorithm of cancellation error voltage,and considering the skin effect.Based on the approach of equivalent motor idling,mutual inductance is identified more accurately through injecting the very low frequency single phase alternating current and eliminating the influence of the rotor resistance.All the IM parameters estimated in the standstill state is compared with the IM parameters measured by the traditional method and used in the sensor-less vector control system.The experimental results show that the proposed parameter identification algorithm has high accuracy,practicality,and robustness.

Research Center of Photovoltaic System Engineering of Ministry of Education Hefei University of Technology Hefei 230009 China

基于异步电动机的非对称T型模型,提出一种电动机静止状态下参数辨识的改进算法。分析并指出逆变器死区只对输出电压有功分量产生影响,并通过对死区自适应补偿方法辨识出电动机参数,提高了辨识的准确度。考虑到趋肤效应的影响,给出通过两次注入相同转差频率、不同幅值的单相交流电流,并通过对误差电压进行对消的自适应算法辨识出转子电阻;基于等效空载的方法,注入极低频率的单相交流电流使电动机在静止状态与空载旋转状态等效,避免了转子电阻的影响,从而更精确的辨识出互感。将所测量参数与利用传统方法测量的参数进行对比,并将参数用于无速度传感器矢量控制,验证了该算法具有较高的精确性、实用性和鲁棒性。

... 由文献[13]可知,由死区造成的误差电压的一般表达式为 ...

2018

0.0

... 2 场路联合有限元仿真为了准确地辨识直线感应电机的参数,考虑到直线感应电机初、次级漏感不相等和边端效应的影响,以及死区效应对参数辨识精度的影响,采用场路联合有限元仿真,在Ansys Maxwell中搭建单边直线感应电机的3D模型,在Simplore中搭建PWM逆变电路,来控制施加给直线感应电机的激励^[14] ...

1991

0.0

... s^[15],因此将死区时间 Te分别设置为0、1、2、3、4 #cod#x003bc ...