智能网联车环境下异质交通流稳定性及安全性分析

引用本文

蒋阳升, 胡蓉, 姚志洪, 吴培财, 罗孝羚. 智能网联车环境下异质交通流稳定性及安全性分析[J]. 北京交通大学学报, 2020,44(1): 27-33.
JIANG Yangsheng, HU Rong, YAO Zhihong, WU Peicai, LUO Xiaoling. Stability and safety analysis for heterogeneous traffic flow composed of intelligent and connected vehicles[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2020,44(1): 27-33.
Doi:10.11860/j.issn.1673-0291.20190045 复制到剪切板

Permissions

北京交通大学学报编辑部所有

智能网联车环境下异质交通流稳定性及安全性分析

蒋阳升^1a,^1b, 胡蓉^1a,^1b, 姚志洪^1a,^1b,², 吴培财³, 罗孝羚^1a,^1b

1.西南交通大学 a.交通运输与物流学院,b.综合交通大数据应用技术国家工程实验室, 成都 611756

2.重庆交通大学重庆市交通运输工程重点实验室,重庆 400074

3.厦门金美信消费金融有限责任公司,福建厦门 361008

通信作者:姚志洪(1991—),男,安徽安庆人,讲师,博士. email: zhyao@my.swjtu.edu.cn.

第一作者:蒋阳升(1976—),男,湖南衡阳人,教授,博士.研究方向为交通系统优化. email: jiangyangsheng@swjtu.cn.

收稿日期: 2019-04-10

基金: 国家自然科学基金(51578465, 71771190); 重庆市交通运输工程重点实验室开放基金项目(2018TE01); 西南交通大学2019年研究生学术素养提升计划(2019KCJS46)

摘要

针对未来道路上由人工驾驶车辆(Human Driven Vehicles,HDVs)和智能网联车(Intelligent and Connected Vehicles, ICVs)所组成的异质交通流,对其稳定性与安全性进行研究.首先,利用全速度差模型(Full Velocity Difference, FVD)和协同自适应巡航控制模型(Cooperative Adaptive Cruise Control, CACC)分别描述人工驾驶车辆和智能网联车的跟驰特性.然后,通过分析不同智能网联车渗透率下异质交通流的线性稳定性,得出其稳定性条件.最后,采用数值仿真实验进行验证,选取多项安全指标评估了不同渗透率下异质交通流的安全性.结果表明:随着渗透率的增加,交通流的车速离散程度减小,即表示安全性能提高;安全指标降低比例减少,即表示交通安全风险降低.因此,智能网联车的应用有助于提高交通安全.

关键词: 智能交通; 智能网联车; 稳定性; 安全性; 跟驰模型; 异质交通流

中图分类号:U491 文献标志码:A 文章编号:1673-0291(2020)01-0027-07

Stability and safety analysis for heterogeneous traffic flow composed of intelligent and connected vehicles

JIANG Yangsheng^1a,^1b, HU Rong^1a,^1b, YAO Zhihong^1a,^1b,², WU Peicai³, LUO Xiaoling^1a,^1b

1a. School of Transportation and Logistics, 1b. National Engineering Laboratory for Integrated Transportation Big Data Application Technology,Southwest Jiaotong University, Chengdu 611756,China

2. Chongqing Key Laboratory of Transportation Engineering, Chongqing Jiaotong University, Chongqing 400074, China

3. JMX Consumer Finance Co.,Ltd., Xiamen Fujian 361008, China

Fund:Foundation items:National Natural Science Foundation of China(51578465, 71771190); Open Fund Project for the Chongqing Municipal Transportation Engineering Key Laboratory(2018TE01); Southwest Jiaotong University Graduate Academic Training and Promotion Program (2019KCJS46)

Abstract

On future roads,the heterogeneous traffic flow will be composed of Human Driven Vehicles (HDVs) and Intelligent and Connected Vehicles (ICVs), focusing on which their stability and safety performance are studied in this paper. Firstly, the Full Velocity Difference (FVD) model and Cooperative Adaptive Cruise Control (CACC)following model are adopted to describe the car-following characteristics of the HDVs and ICVs. Then the stability conditions of heteroge neous traffic flow under different penetration rates of the ICVs are obtained by analyzing the linear stability. Finally, a numerical simulation of heterogeneous traffic flow is designed for verification, and the safety performance of heterogeneous traffic flow under different penetration rates is evaluated by multiple safety indexes. The results show that as the penetration rate increases, the dispersion degree of the vehicle speed in heterogeneous traffic flow decreases, which means that it becomes safer. The reduction ratio of the safety index decreases with the increase of penetration rate, which indicates the safety risk is reduced. Therefore, the application of ICVs can improve traffic safety.

Keyword: intelligent transportation; intelligent and connected vehicles; stability; safety; car-following model; heterogeneous traffic flow

文章图片

近年来, 随着国家智能网联汽车发展的相关战略的提出, 智能网联车的研究^{[1, 2, 3]}和规模化应用将对道路交通流产生巨大的影响.但最新研究表明^[4], 2050年道路上智能网联车的渗透率仅能达到75%, 未来道路交通将会普遍呈现由人工驾驶车辆和智能网联车组成的异质交通流特征.因此, 研究该异质交通流的稳定性和安全性具有重要的理论和实践意义.

国外对于智能网联车环境下异质交通流安全性的研究起步较早.Lee等^[5]经过实地真车实验进行自适应巡航(Adaptive Cruise Control, ACC)系统的交通安全性能分析, 证明ACC车辆可改善对前车轻微与中度刹车的车辆尾部碰撞安全隐患.Moon等^[6]构建了ACC模型, 选取碰撞时间(Time-to-collision, TTC)进行交通安全评估, 指出ACC跟驰模型能使车辆与车辆间保持安全距离.Li等^{[7, 8]}分别研究了CACC系统、ACC参数设置对于降低高速公路尾部碰撞风险的影响, 利用TTC的两个替代指标碰撞暴露时间(Time Exposed Time-to-collision, TET)与碰撞接触时间(Time Integrated Time-to-collision, TIT)评估碰撞风险, 表明CACC或者ACC渗透率的增加有利于提升安全效果.Jeong等^[9]通过优化车辆操纵控制分析了异质交通流的碰撞风险, 表明自动驾驶车辆渗透率的提高有利于减少车辆碰撞.而在国内, 秦严严等^{[10, 11]}分别考虑了网联辅助驾驶系统退化机制、控制输出的网联车辆(Connected and Automated Vehicles, CAV)反馈系数, 分析与优化了异质交通流的线性稳定性, 从而降低异质交通流中的车辆追尾风险.刘新雨等^[12]利用驾驶模拟器进行实际道路驾驶实验, 比较分析了不同特性的驾驶员的应激反应, 指出ACC驾驶的安全性取决于驾驶员对于ACC的认知度.从以上分析可知, 研究混有智能网联车的异质交通流稳定性和安全性尤其重要.但现有研究仍存在以下两点不足:1)现有大多研究仅采用尾部碰撞风险作为单一指标来评价智能网联车环境下的异质交通流安全性, 评价指标单一.而现有研究表明, 采用多指标才能全面地评价异质交通流的安全性; 2)大多研究并未同时对混有智能网联车异质交通流的稳定性和安全性进行分析.

为解决该问题, 本文作者拟研究混有智能网联车异质交通流的稳定性, 得出异质交通流稳定时对应的智能网联车渗透率条件.同时, 引入多指标安全评价体系来全面地解析异质交通流的安全性, 弥补单一安全指标评估的不足.本文中采用的智能网联车环境为由智能网联车和普通车辆组成的混合交通流环境, 其中智能网联车之间可以相互通信, 且车辆采用自动控制模式, 与普通车辆的跟驰行为相比, 智能网联车具有更加高效和安全的跟驰特性.因此, 首先采用FVD模型^[13]与CACC模型分别描述人工驾驶车辆和智能网联车辆的驾驶行为, 再在此基础上推导了异质交通流稳定性条件.然后, 利用数值仿真实验, 选取车速标准差(Standard Deviation of Speed, SD)、TET、TIT与追尾碰撞风险指数(Time Exposed Rear-end Crash Risk Index, TERCRI)^[14]等多项安全评价指标来评估异质交通流的安全性.

1 跟驰模型

1.1 人工驾驶车辆跟驰模型

FVD模型弥补了广义力模型与优化速度模型的诸多不足, 常被应用于人工驾驶车辆跟驰行为研究.其考虑了速度差项和车间距, 并通过实际数据对该模型进行了参数标定, 其模型为

$\dot{v} = κ [V (△ x) - v] + \frac{λ}{△ x - L} △ v$ (1)

式中: $\dot{v}$ 为车辆速度的导数, m/s²; $κ 、 λ$ 均为模型的敏感系数; $△ x$ 为本车与其前车的车头间距, m; $v$ 为车速, m/s; $L$ 为车辆长度, m; $△ v$ 为本车与其前

车的速度差, m/s; $V (△ x)$ 为优化速度函数, 即

$V (△ x) = v_{f} [1 - \exp (- \frac{α}{v_{f}} (△ x - L - s_{0})]$ (2)

式中: $v_{f}$ 为自由流速度, m/s; $α$ 为敏感系数; $s_{0}$ 为最小安全间距, m.

该模型的相关参数取值如表1所示, 其标定误差为4.02%^[15].

表1 FVD模型参数的标定取值 Tab.1 Calibrated values of FVD model parameters

参数	取值	参数	取值
$κ /$ s^-1	0.629	$v_{f} / (m \cdot s^{- 1})$	33.0
$λ /$ s^-1	4.10	$s_{0} / m$	2.46
$α /$ s^-1	1.26	$L / m$	5.0

表1 FVD模型参数的标定取值 Tab.1 Calibrated values of FVD model parameters

1.2 智能网联车跟驰模型

相比较于其他的跟驰模型, CACC模型是基于恒定车间时距而未考虑其他驾驶策略的跟驰模型, 其是由加州伯克利大学PATH实验室通过真车测试实验, 基于真车数据, 更能真实地描述了CACC车辆恒定车间时距的跟驰特性.因此, 采用CACC模型描述智能网联车的跟驰行为, 其模型^[7]的数学表达式为

$\{\begin{array}{l} v = v_{p} + k_{p} e + k_{d} \dot{e} \\ e = △ x - s_{0} - L - t_{c} v \end{array}$ (3)

式中: $v_{p}$ 为前一个控制时间的后车速度, m/s; $e$ 为实际车间距与期望车间距的误差, m; $e$ 的导数形式为 $\dot{e}$ ; $t_{c}$ 为期望车间时距, s; $k_{p}$ 和 $k_{d}$ 为控制系数.

对式(3)中的速度求导为

$\dot{v} = \frac{k_{p} (△ x - s_{0} - L) - k_{p} t_{c} v + k_{d} △ v}{k_{d} t_{c} + Δ t}$ (4)

式中: $Δ t$ 为时间.由真车数据标定后的CACC模型能较好地体现智能网联车的跟驰特性, 其参数取值^[16]为 $k_{p} = 0.45, k_{d} = 0.25, Δ t = 0.01 s, t_{c} = 0.6 s .$

2 交通流稳定性分析

2.1 稳定性定义

交通流稳定性是分析道路中出现的随机扰动对于交通流状态影响的重要方法.交通流不稳定容易引起交通堵塞, 进而使道路交通通行效率降低, 故稳定性分析对道路交通安全的评价至关重要.交通流非稳定状态时的条件^[17]为

$F = \frac{1}{2} {(f_{v})}^{2} - f_{△ v} f_{v} - f_{△ x} < 0$ (5)

当交通流不满足稳定状态时, 满足式(5)中的条件.其中, $f_{v} 、 f_{△ v} 、 f_{△ x}$ 分别为跟驰模型关于车辆速度、速度差和车头间距的偏微分方程, 即

$\{\begin{array}{l} f_{v} = \frac{\partial f (v, △ v, △ x)}{\partial v} |_{(v^{*}, 0, △ x^{*})} \\ f_{△ v} = \frac{\partial f (v, △ v, △ x)}{\partial △ v} |_{(v^{*}, 0, △ x^{*})} \\ f_{△ x} = \frac{\partial f (v, △ v, △ x)}{\partial △ x} |_{(v^{*}, 0, △ x^{*})} \end{array}$ (6)

式中: $v^{*}$ 为平衡态下的速度, m/s; $△ x^{*}$ 为平衡态下的车头间距, m.

2.2 同质交通流稳定性分析

分别对人工驾驶车辆和智能网联车组成的同质交通流进行稳定性分析.首先, 将FVD跟驰模型式(1)带入式(6)求偏微分, 可得

$\{\begin{array}{l} {f^{H}}_{v} = - κ \\ {f^{H}}_{△ v} = \frac{λα}{α s_{0} - v_{f} \ln (1 - v / v_{f})} \\ {f^{H}}_{△ x} = κα (1 - v / v_{f}) \end{array}$ (7)

式中: ${f^{H}}_{v} 、 {f^{H}}_{△ v} 、 {f^{H}}_{△ x}$ 分别为人工驾驶车辆模型关于车辆速度、速度差和车头间距的求偏微分项.

同理, 将式(3)CACC模型带入式(6)求偏微分, 可得

$\{\begin{array}{l} {f^{I}}_{v} = - \frac{k_{p} t_{c}}{k_{d} t_{c} + Δ t} \\ {f^{I}}_{△ v} = \frac{k_{d}}{k_{d} t_{c} + Δ t} \\ {f^{I}}_{△ x} = \frac{k_{p}}{k_{d} t_{c} + Δ t} \end{array}$ (8)

式中: ${f^{I}}_{v} 、 {f^{I}}_{△ v} 、 {f^{I}}_{△ x}$ 则分别为智能网联车模型关于车辆速度、速度差和车头间距的求偏微分项.

利用交通流稳定状态时的判别条件, 可分别计算同质交通流中FVD模型非稳定性约束判别值 $F_{H}$ 与CACC模型的非稳定性约束判别值 $F_{I}$ 为

$F_{H} = \frac{1}{2} {({f^{H}}_{v})}^{2} - {f^{H}}_{△ v} {f^{H}}_{v} - {f^{H}}_{△ x}$ (9)

$F_{I} = \frac{1}{2} {({f^{I}}_{v})}^{2} - {f^{I}}_{△ v} {f^{I}}_{v} - {f^{I}}_{△ x}$ (10)

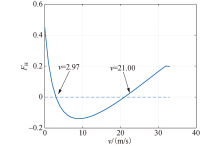
由式(9)计算可知, 当车辆速度在范围区间0~2.97 m/s与21~33 m/s内时, 由人工驾驶车辆组成的同质交通流处于稳定状态, 其稳定性判别值与车速值的关系如图1所示.

	Figure Option View Download New Window
	图1 FVD模型稳定性分析Fig.1 Stability analysis of FVD model

同理, 将式(8)带入式(10)可计算智能网联车的稳定性判别值为

$\begin{array}{l} F_{I} = \frac{k_{p} t_{c} (k_{p} t_{c} + 2 k_{d})}{2 (k_{d} t_{c} {+ Δ t)}^{2}} - \\ \frac{k_{p}}{k_{d} t_{c} + Δ t} = 1.248 > 0 \end{array}$ (11)

由式(11)可知, 由智能网联车组成的同质交通流的线性稳定判别条件取值为1.248, 恒大于0, 其稳定性判别值与车速无关, 故智能网联车在不同速度范围内均处于稳定状态.

2.3 异质交通流稳定性分析

异质交通流是由人工驾驶车辆和智能网联车组成的, 可推导得出异质交通流非稳定性条件^[17]为

$\overset{N}{\sum_{n = 1}} [\frac{1}{2} {(f_{v}^{n})}^{2} - f_{△ v}^{n} f_{v}^{n} - f_{△ x}^{n}] {(\prod_{m \neq n} f_{△ x}^{m})}^{2} < 0$ (12)

式中: $n 、 m$ 为车辆的编号; $f_{v}^{n} 、 f_{△ v}^{n} 、 f_{△ x}^{n}$ 为第 $n$ 辆车的控制公式关于车辆速度、速度差与车头间距的求偏微分项.

假设异质交通流中车辆总数为 $N$ , 智能网联车渗透率为 $p$ , 则智能网联车与人工驾驶车辆的比例为 $p : (1 - p)$ , 则将式(1)和(3)带入(12)计算得

$\begin{array}{l} N (1 - p) [0.5 {({f^{H}}_{v})}^{2} - {f^{H}}_{△ v} {f^{H}}_{v} - {f^{H}}_{△ x}] \times \\ {[{({f^{H}}_{Δ x})}^{N (1 - p) - 1} {({f^{I}}_{Δ x})}^{Np}]}^{2} + \\ Np [0.5 {({f^{I}}_{v})}^{2} - {f^{I}}_{△ v} {f^{I}}_{v} - {f^{I}}_{△ x}] \times \\ {[{({f^{H}}_{Δ x})}^{N (1 - p)} {({f^{I}}_{Δ x})}^{Np - 1}]}^{2} < 0 \end{array}$ (13)

由式(13)简化为

$\begin{array}{l} \frac{(1 - p) [0.5 {({f^{H}}_{v})}^{2} - {f^{H}}_{△ v} {f^{H}}_{v} - {f^{H}}_{△ x}]}{{({f^{H}}_{△ x})}^{2}} + \\ \frac{p [0.5 {({f^{I}}_{v})}^{2} - {f^{I}}_{△ v} {f^{I}}_{v} - {f^{I}}_{△ x}]}{{({f^{I}}_{Δ x})}^{2}} < 0 \end{array}$ (14)

令 $G_{H} 、 G_{I}$ 取值为

$G_{H} = \frac{0.5 {({f^{H}}_{v})}^{2} - {f^{H}}_{△ v} {f^{H}}_{v} - {f^{H}}_{△ x}}{{({f^{H}}_{△ x})}^{2}} = \frac{F_{H}}{{({f^{H}}_{△ x})}^{2}}$ (15)

$G_{I} = \frac{0.5 {({f^{I}}_{v})}^{2} - {f^{I}}_{△ v} {f^{I}}_{v} - {f^{I}}_{△ x}}{{({f^{I}}_{Δ x})}^{2}} = \frac{F_{I}}{{({f^{I}}_{Δ x})}^{2}}$ (16)

则式(14)可表示为

$G = (1 - p) G_{H} + p G_{I} < 0$ (17)

式中: $G$ 为异质交通流稳定性判别值; $G_{H}$ 为异质交通流稳定性判别值中的人工驾驶车辆部分; $G_{I}$ 为异质交通流稳定性判别值中的智能网联车部分.

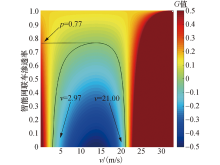
由式(17)的计算结果可知:异质交通流的稳定性与智能网联车渗透率存在一定的关系, 绘制出不同渗透率下的稳定值图, 如图2所示.其中, 黑色曲线表示在稳定值 $G = 0$ 的条件下, 所对应的不同渗透率与其速度值.

	Figure Option View Download New Window
	图2 异质交通流稳定性分析Fig.2 Stability analysis of heterogeneous traffic flow

由图2知, 黑色曲线表示异质交通流处于稳定状态时的临界值 $G = 0$ .曲线下方区域的异质交通流为不稳定状态, 曲线上方的异质交通流为稳定状态, 该稳定状态下渗透率的最小取值为0.77, 即当渗透率大于77%时, 异质交通流均处于稳定状态.曲线与横轴的两交点表示:当渗透率为0时, 人工驾驶车辆稳定状态的速度临界点为2.97 m/s与21.00 m/s, 这与同质交通流的分析结果一致.同时, 需要说明, 该渗透率边界值是由文中模型分析得出, 而现有文献[8]研究表明, 不同的跟驰模型得出的结果可能不一致.稳定性结果和渗透率边界值与不同模型的选择和模型参数共同决定.

3 交通流安全性分析

影响交通安全的因素涉及道路环境、车辆性能和人为因素等.现有研究采用微观交通安全指标对交通安全进行评价, 这些指标包括车速标准差SD、碰撞时间TTC和碰撞风险指数等.为全面评价混有智能网联车异质交通流的安全性, 本文拟采用SD、TET、TIT与TERCRI等4项指标来作为评估标准.

3.1 安全性指标

车速离散被广泛应用于估算交通安全程度, 通常采用车速标准差 $SD$ 值来描述整个交通流车辆速度的离散程度, 其计算公式为

$SD = σ = \sqrt[]{\frac{\overset{N}{\sum_{n = 1}} {(v_{n} - \overset{̅}{v})}^{2}}{N - 1}}$ (18)

式中: $\overset{̅}{v}$ 表示所有车辆的速度平均值, m/s.通常处于不稳定状态的车流具有较高的 $SD$ 值, 其安全性较低; 相反, 较低 $SD$ 值代表车流整体中各车速度接近, 安全性较好.

碰撞时间TTC表示当保持速度差时, 前车与后车发生碰撞之前的剩余时间, 其表达式可表示为^[6]

$\begin{array}{l} TT C_{n} (t) = \frac{x_{n - 1} (t) - x_{n} (t) - L}{v_{n} (t) - v_{n - 1} (t)}, \\ v_{n} (t) > v_{n - 1} (t) \end{array}$ (19)

进一步, 基于该公式, 可计算TET和TIT两个安全性能指标

$TET (t) = \overset{N}{\sum_{n = 1}} \overset{M}{\sum_{t = 0}} δ_{t}, δ_{t} = \{\begin{array}{l} 1, 0 < TT C_{n} (t) < TT C^{*} \\ 0, 其他 \end{array}$ (20)

$TIT (t) = \overset{N}{\sum_{n = 1}} \overset{M}{\sum_{t = 0}} [TT C^{*} - TT C_{n} (t)], 0 < TT C_{n} (t) < TT C^{*}$ (21)

式中: $TT C_{n} (t)$ 表示当时间为t时车辆的TTC值,s; $x_{n - 1} (t) 、 x_{n} (t)$ 分别为前、后车车辆位置, m; $v_{n - 1} 、 v_{n}$ 分别为前、后车车辆速度, m/s; $M$ 为仿真步长总数; $TT C^{*}$ 为碰撞时间的阈值^[18], 其取值为1~3 s.

当前车速度骤减, 由于前后车辆之间的安全距离不足所造成追尾事故的危险程度采用TERCRI进行描述, 其表达式^[14]为

$\begin{array}{l} TERCRI (t) = \overset{N}{\sum_{n = 1}} \overset{M}{\sum_{t = 0}} RCR I_{n} (t) \times Δ t, \\ RCR I_{n} (t) = \{\begin{array}{l} 1, D_{F} > D_{L} \\ 0, D_{F} \leq D_{L} \end{array} \end{array}$ (22)

其中, $D_{L} 、 D_{F}$ 分别为前、后车的停车距离, 即

$\{\begin{array}{l} D_{L} = v_{n - 1} h + \frac{{v^{2}}_{n - 1}}{2 a_{n - 1}} + L \\ D_{F} = v_{n} t_{PRT} + \frac{{v^{2}}_{n}}{2 a_{n}} \end{array}$ (23)

式中: $h$ 为车头时距, s; $a_{n - 1} 、 a_{n}$ 为前、后车车辆加速度, 取值为3.42 m/s²; $t_{PRT}$ 为感知-反应时间, 取值为1.5 s.

3.2 仿真实验验证

为分析不同智能网联车渗透率条件下的异质交通流安全性, 参考文献[19], 不考虑车辆换道行为, 采用数值仿真实验模拟单车道中车辆的跟驰行为, 其中仿真路段长度为6.5 km, 路段中间为匝道汇入, 主路和匝道上游交通需求分别为1 700 veh/h和360 veh/h.车辆到达采用泊松分布模拟, 产生车辆的同时产生1个在[0, 1]之间的随机数.若随机数不大于给定的渗透率, 则该车辆采用智能网联车的跟驰模型; 否则为人工驾驶车辆的跟驰行为.仿真时长为1 h, 仿真精度为0.1 s, 前5 min为仿真预热时间.所有仿真实验均在数值仿真软件Matlab中实现, 仿真实验电脑配置为Intel 3.60 GHz CPU和8 GB运行内存.为探讨智能网联车渗透率对交通流安全的影响, 分别仿真渗透率为0%、20%、40%、60%、80%和100%等6种场景.同时, 为避免仿真实验随机性的影响, 每种场景采用不同的随机种子各仿真3次, 取仿真结果的平均值作为最终结果.最后, 根据仿真数据计算对应渗透率下的安全指标.依据计算结果判断不同渗透率下异质交通流的安全性.

获取仿真数据后, 可由式(18)计算6种智能网联车渗透率下的 $SD$ 值, 得出不同渗透率下的仿真实验值, 如表2所示.

表2 不同渗透率下SD的平均值 Tab.2 SD average under different penetration rates

由表2可知, $SD$ 平均值随着智能网联车渗透率的增加而降低.该结果表明, 当智能网联车渗透率为0%时, 车速离散值最大, 即交通流的安全性能低; 当渗透率为80%及以上时, $SD$ 平均值小于1, 车速离散值很小.此时, 车流中各车辆速度比较接近, 安全性能较好.因此, 从对 $SD$ 的分析可知, 智能网联车能够有效改善交通流的安全性.

同时, 考虑到阈值 $TT C^{*}$ 取值范围为1~3s, 由式(19)~(21)计算不同 $TT C^{*}$ 取值下的TET和TIT两项指标, 如图3所示.图3中, 颜色条表示TET和TIT指标降低比例的大小, 当颜色越深时, 所降低的比例越小.

	Figure Option View Download New Window
	图3 TET和TIT指标降低比例的热力分析Fig.3 Thermal analysis of indexes TET and TIT reduction ratio

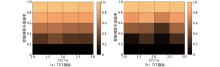
由TET和TIT指标降低比例的热力图分析可知, 随着渗透率的提高, TET与TIT指标值降低的比例越大, 代表着交通安全风险越小.为更形象地描述不同 $TT C^{*}$ 取值下的TET和TIT的降低比例, 可绘制TET和TIT的降低比例变化的曲线图, 如图4所示.

	Figure Option View Download New Window
	图4 碰撞时间TET和TIT指标降低比例Fig.4 Reduction ratio of indexes TET and TIT

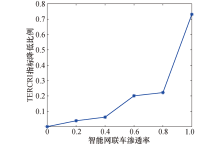
当阈值变化时, 虽然TET与TIT降低比例范围有一定波动, 但是整体趋势一致, 均随着渗透率增加而增加.当全部为智能网联车, 两项指标降低比例最大, 故阈值取值大小对安全指标的计算影响较小.依据仿真实验结果, 由式(23)计算前后车辆停车距离, 进而分析车辆追尾碰撞风险TERCRI指标相对于渗透率为0时所降低的比例, 可绘制不同渗透率下的降低比例变化曲线图, 如图5所示.

	Figure Option View Download New Window
	图5 TERCRI指标降低比例趋势Fig.5 Reduction ration changing trend of index TERCRI

由图5可知, 车辆之间处于不安全距离的风险随着渗透率增加而逐渐降低, 且当渗透率大于80%时, 降低效果更明显.这也表明智能网联车的应用能够有效改善交通流的安全.

4 结论

1)在同质交通流中, 人工驾驶车辆的交通流稳定速度区间为0~2.97 m/s和21~33 m/s; 而智能网联车在不同速度区间下均处于稳定状态.

2)当智能网联车渗透率大于77%时, 异质交通流不受速度区间的影响, 均处于稳定状态.

3)车速离散值随着渗透率的增加而降低; TET、TIT与TERCRI指标降低比例随着渗透率增加而提高; 当智能网联车渗透率大于80%时, 车速离散值较小, 车辆尾部碰撞风险明显降低, 安全性能大大提高.这些指标均表明智能网联车能够有效地提高交通安全, 为未来智能网联车环境下的交通安全管理提供一定的理论参考.

4)不同TTC阈值条件下, TET与TIT整体趋势一致, TTC阈值对于实验结果的影响较小.

参考文献

文献列表

[1]	王青龙, 乔瑞, 樊娜, 等. 一种面向车联网的高效条件匿名认证方案[J]. 北京交通大学学报, 2019, 43(5): 80-86. WANG Qinglong, QIAO Rui, FAN Na, et al. An efficient conditional anonymity authentication scheme for VANETs[J]. Journal of Beijing Jiaotong University, 2019, 43(5): 80-86. (in Chinese) [本文引用:1]
[2]	姚志洪, 蒋阳升, 王逸, 等. 车联网环境下的动态异质交通流车队离散模型[J]. 北京交通大学学报, 2019, 43(2): 107-116. YAO Zhihong, JIANG Yangsheng, WANG Yi, et al. Discrete model of dynamic heterogeneous traffic flow platoon in Internet of vehicles[J]. Journal of Beijing Jiaotong University, 2019, 43(2): 107-116. (in Chinese) [本文引用:1]
[3]	柴琳果, 蔡伯根, 上官伟, 等. 车联网干线协调控制相位差自适应优化[J]. 北京交通大学学报, 2018, 42(2): 69-75. CHAI Linguo, CAI Baigen, SHANGGUAN Wei, et al. Offset adaptive optimizing of arterial coordinating under Internet of vehicle[J]. Journal of Beijing Jiaotong University, 2018, 42(2): 69-75. (in Chinese) [本文引用:1]
[4]	BANSAL P, KOCKELMAN K M. Forecasting Americans’ long-term adoption of connected and autonomous vehicle technologies[J]. Transportation Research Part A: Policy and Practice, 2017, 95: 49-63. [本文引用:1]
[5]	LEE J D, MCGEHEE D V, BROWN T L, et al. Effects of adaptive cruise control and alert modality on driver performance[J]. Transportation Research Record: Journal of the Transportation Research Board, 2006, 1980(1): 49-56. [本文引用:1]
[6]	MOON S, MOON I, YI K. Design, tuning, and evaluation of a full-range adaptive cruise control system with collision avoidance[J]. Control Engineering Practice, 2009, 17(4): 442-455. [本文引用:2]
[7]	LI Y, WANG H, WANG W, et al. Evaluation of the impacts of cooperative adaptive cruise control on reducing rear-end collision risks on freeways[J]. Accident Analysis & Prevention, 2017, 98: 87-95. [本文引用:2]
[8]	LI Y, LI Z B, WANG H, et al. Evaluating the safety impact of adaptive cruise control in traffic oscillations on freeways[J]. Accident Analysis & Prevention, 2017, 104: 137-145. [本文引用:2]
[9]	JEONG E, OH C, LEE S. Is vehicle automation enough to prevent crashes? Role of traffic operations in automated driving environments for traffic safety[J]. Accident Analysis & Prevention, 2017, 104: 115-124. [本文引用:1]
[10]	秦严严, 王昊, 王炜. 网联辅助驾驶混合交通流稳定性及安全性分析[J]. 东南大学学报(自然科学版), 2018, 48(1): 188-194. QIN Yanyan, WANG Hao, WANG Wei. Analysis on stability and safety for mixed traffic flow with connected auxiliary driving[J]. Journal of Southeast University(Natural Science Edition), 2018, 48(1): 188-194. (in Chinese) [本文引用:1]
[11]	秦严严, 王昊. 智能网联车辆交通流优化对交通安全的改善[J]. 中国公路学报, 2018, 31(4): 202-210. QIN Yanyan, WANG Hao. Improving traffic safety via traffic flow optimization of connected and automated vehicles[J]. China Journal of Highway and Transport, 2018, 31(4): 202-210. (in Chinese) [本文引用:1]
[12]	刘新雨, 吴学勤, 王畅, 等. 自适应巡航控制系统对驾驶安全性的影响研究[J]. 中国安全科学学报, 2017, 27(4): 43-48. LIU Xinyu, WU Xueqin, WANG Chang, et al. Impact of adaptive cruise control system on driving safety[J]. China Safety Science Journal, 2017, 27(4): 43-48. (in Chinese) [本文引用:1]
[13]	JIANG R, WU Q S, ZHU Z. Full velocity difference model for a car-following theory[J]. Physical Review E, 2001, 64: 017101. [本文引用:1]
[14]	RAHMAN M S, ABDEL-ATY M. Longitudinal safety evaluation of connected vehicles’ platooning on expressways[J]. Accident Analysis & Prevention, 2018, 117: 381-391. [本文引用:2]
[15]	WANG H, WANG W, CHEN J, et al. Estimating equilibrium speed-spacing relationship from dynamic trajectory data[C]//Transportation Research Board 91st Annual Meeting. Washington, 2012: 1-18. [本文引用:1]
[16]	MILANES V, SHLADOVER S E. Modeling cooperative and autonomous adaptive cruise control dynamic responses using experimental data[J]. Transportation Research Part C: Emerging Technologies, 2014, 48: 285-300. [本文引用:1]
[17]	WARD J A. Heterogeneity, lane-changing and instability in traffic: a mathematical approach[D]. Bristol: University of Bristol, 2009. [本文引用:2]
[18]	MINDERHOUD M M, BOVY P H L. Extended time-to-collision measures for road traffic safety assessment[J]. Accident Analysis & Prevention, 2001, 33(1): 89-97. [本文引用:1]
[19]	TALEBPOUR A, MAHMASSANI H S. Influence of connected and autonomous vehicles on traffic flow stability and throughput[J]. Transportation Research Part C: Emerging Technologies, 2016, 71: 143-163. [本文引用:1]

2019

0.0

王青龙, 乔瑞, 樊娜, 等. 一种面向车联网的高效条件匿名认证方案[J]. 北京交通大学学报, 2019, 43(5): 80-86.

WANG

Qinglong

, QIAO

Rui

, FAN

, et al. An efficient conditional anonymity authentication scheme for VANETs[J]. Journal of Beijing Jiaotong University, 2019, 43(5): 80-86. (in Chinese)

... 近年来,随着国家智能网联汽车发展的相关战略的提出,智能网联车的研究^[1,2,3]和规模化应用将对道路交通流产生巨大的影响 ...

2019

0.0

姚志洪, 蒋阳升, 王逸, 等. 车联网环境下的动态异质交通流车队离散模型[J]. 北京交通大学学报, 2019, 43(2): 107-116.

YAO

Zhihong

, JIANG

Yangsheng

, WANG

, et al. Discrete model of dynamic heterogeneous traffic flow platoon in Internet of vehicles[J]. Journal of Beijing Jiaotong University, 2019, 43(2): 107-116. (in Chinese)

... 近年来,随着国家智能网联汽车发展的相关战略的提出,智能网联车的研究^[1,2,3]和规模化应用将对道路交通流产生巨大的影响 ...

2018

0.0

柴琳果, 蔡伯根, 上官伟, 等. 车联网干线协调控制相位差自适应优化[J]. 北京交通大学学报, 2018, 42(2): 69-75.

CHAI

Linguo

, CAI

Baigen

, SHANGGUAN

Wei

, et al. Offset adaptive optimizing of arterial coordinating under Internet of vehicle[J]. Journal of Beijing Jiaotong University, 2018, 42(2): 69-75. (in Chinese)

... 近年来,随着国家智能网联汽车发展的相关战略的提出,智能网联车的研究^[1,2,3]和规模化应用将对道路交通流产生巨大的影响 ...

2017

0.0

... 但最新研究表明^[4],2050年道路上智能网联车的渗透率仅能达到75%,未来道路交通将会普遍呈现由人工驾驶车辆和智能网联车组成的异质交通流特征 ...

2006

0.0

... Lee等^[5]经过实地真车实验进行自适应巡航(Adaptive Cruise Control,ACC)系统的交通安全性能分析,证明ACC车辆可改善对前车轻微与中度刹车的车辆尾部碰撞安全隐患 ...

2009

0.0

... Moon等^[6]构建了ACC模型,选取碰撞时间(Time-to-collision,TTC)进行交通安全评估,指出ACC跟驰模型能使车辆与车辆间保持安全距离 ...

... 碰撞时间TTC表示当保持速度差时,前车与后车发生碰撞之前的剩余时间,其表达式可表示为^[6] ...

2017

0.0

... Li等^[7,8]分别研究了CACC系统、ACC参数设置对于降低高速公路尾部碰撞风险的影响,利用TTC的两个替代指标碰撞暴露时间(Time Exposed Time-to-collision, TET)与碰撞接触时间(Time Integrated Time-to-collision, TIT)评估碰撞风险,表明CACC或者ACC渗透率的增加有利于提升安全效果 ...

... 因此,采用CACC模型描述智能网联车的跟驰行为,其模型^[7]的数学表达式为 ...

2017

0.0

... 同时,需要说明,该渗透率边界值是由文中模型分析得出,而现有文献[8]研究表明,不同的跟驰模型得出的结果可能不一致 ...

2017

0.0

... Jeong等^[9]通过优化车辆操纵控制分析了异质交通流的碰撞风险,表明自动驾驶车辆渗透率的提高有利于减少车辆碰撞 ...

2018

0.0

秦严严, 王昊, 王炜. 网联辅助驾驶混合交通流稳定性及安全性分析[J]. 东南大学学报(自然科学版), 2018, 48(1): 188-194.

QIN

Yanyan

, WANG

Hao

, WANG

Wei

. Analysis on stability and safety for mixed traffic flow with connected auxiliary driving[J]. Journal of Southeast University(Natural Science Edition), 2018, 48(1): 188-194. (in Chinese)

... 而在国内,秦严严等^[10,11]分别考虑了网联辅助驾驶系统退化机制、控制输出的网联车辆(Connected and Automated Vehicles,CAV)反馈系数,分析与优化了异质交通流的线性稳定性,从而降低异质交通流中的车辆追尾风险 ...

2018

0.0

秦严严, 王昊. 智能网联车辆交通流优化对交通安全的改善[J]. 中国公路学报, 2018, 31(4): 202-210.

QIN

Yanyan

, WANG

Hao

. Improving traffic safety via traffic flow optimization of connected and automated vehicles[J]. China Journal of Highway and Transport, 2018, 31(4): 202-210. (in Chinese)

2017

0.0

刘新雨, 吴学勤, 王畅, 等. 自适应巡航控制系统对驾驶安全性的影响研究[J]. 中国安全科学学报, 2017, 27(4): 43-48.

LIU

Xinyu

, WU

Xueqin

, WANG

Chang

, et al. Impact of adaptive cruise control system on driving safety[J]. China Safety Science Journal, 2017, 27(4): 43-48. (in Chinese)

... 刘新雨等^[12]利用驾驶模拟器进行实际道路驾驶实验,比较分析了不同特性的驾驶员的应激反应,指出ACC驾驶的安全性取决于驾驶员对于ACC的认知度 ...

2001

0.0

... 因此,首先采用FVD模型^[13]与CACC模型分别描述人工驾驶车辆和智能网联车辆的驾驶行为,再在此基础上推导了异质交通流稳定性条件 ...

2018

0.0

... 然后,利用数值仿真实验,选取车速标准差(Standard Deviation of Speed, SD)、TET、TIT与追尾碰撞风险指数(Time Exposed Rear-end Crash Risk Index, TERCRI)^[14]等多项安全评价指标来评估异质交通流的安全性 ...

... 当前车速度骤减,由于前后车辆之间的安全距离不足所造成追尾事故的危险程度采用TERCRI进行描述,其表达式^[14]为 ...

2012

0.0

... 02%^[15] ...

2014

0.0

... 由真车数据标定后的CACC模型能较好地体现智能网联车的跟驰特性,其参数取值^[16]为 kp=0 ...

2009

0.0

... 交通流非稳定状态时的条件^[17]为 ...

... 3 异质交通流稳定性分析异质交通流是由人工驾驶车辆和智能网联车组成的,可推导得出异质交通流非稳定性条件^[17]为 ...

2001

0.0

... 为碰撞时间的阈值^[18],其取值为1~3 s ...

2016

0.0

... 2 仿真实验验证为分析不同智能网联车渗透率条件下的异质交通流安全性,参考文献[19],不考虑车辆换道行为,采用数值仿真实验模拟单车道中车辆的跟驰行为,其中仿真路段长度为6 ...