引用本文
高雅, 时瑾, 李克飞. 轨底坡对运营地铁轮轨接触特性的影响分析[J]. 北京交通大学学报, 2020,43(6): 25-33.
GAO Ya, SHI Jin, LI Kefei. Influence of rail cant on wheel-rail contact characteristics of operating metro[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2020,43(6): 25-33.
Doi:10.11860/j.issn.1673-0291.20190001  
Permissions
Copyright©2020, 北京交通大学学报编辑部
北京交通大学学报编辑部 所有
轨底坡对运营地铁轮轨接触特性的影响分析
高雅1, 时瑾1, 李克飞2,3
1.北京交通大学 土木建筑工程学院,北京 100044
2.北京市轨道交通建设管理有限公司,北京 100068
3.城市轨道交通全自动运行系统与安全监控北京市重点实验室,北京 100068
通信作者:时瑾(1980—),男,甘肃临夏人,教授,博士,博士生导师.email:jshi@bjtu.edu.cn.

第一作者:高雅(1994—),女(满族),北京市人,博士生.研究方向为线路系统动力学.email:17115278@bjtu.edu.cn.

收稿日期: 2019-01-03
基金: 北京市自然科学基金(8182041); 国家自然科学基金(51578054)
摘要

为研究不同轨底坡条件下实际运营地铁列车的轮轨接触特性,采用轮轨接触空间迹线方法计算分析了轨底坡对轮轨接触几何参数的影响,并建立某地铁B型车辆动力学模型,详细分析了不同线路条件下轨底坡对车辆动力学性能的影响规律.研究表明:LM&CHN60轮轨匹配条件下,轨底坡在1/45~1/20范围内轮轨接触点分布连续,特别是直线段在轨底坡为1/20、曲线段在轨底坡为1/40时轮轨匹配性能良好;运营条件下车轮踏面凹磨造成等效锥度过大,轮轨接触点分布不连续,易造成异常晃车;曲线地段车轮踏面凹磨限制了轮对横向运动,导致轮对对中困难,轮轨接触匹配不良,易造成轮轨滚动接触疲劳.

关键词: 地铁列车; 轮轨接触; 滚动圆半径差; 等效锥度; 轮轨磨耗
中图分类号:U213 文献标志码:A 文章编号:1673-0291(2019)06-0025-09
Influence of rail cant on wheel-rail contact characteristics of operating metro
GAO Ya1, SHI Jin1, LI Kefei2,3
1. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044,China
2. Beijing Metro Construction Administration Corporation Ltd., Beijing 100068,China
3. Automatic Operation System and Safety Monitoring of Urban Rail Transit Beijing Key Laboratory, Beijing 100068,China
Fund:Beijing Municipal Natural Science Foundation(8182041); National Natural Science Foundation of China(51578054)
Abstract

In order to study the wheel-rail contact characteristics of operating metro with different rail cant, the influence of rail cant on wheel-rail contact geometric parameters is analyzed by using the wheel-rail spatial contact geometry algorithm. And the vehicle dynamic model of a B-type metro is established to analyse the influence of rail cant on vehicle dynamics performance under different line conditions. The results are as follows: the wheel-rail contact points of LM&CHN60 profile are continuous when the rail cant is with in the range of 1/45 to 1/20, especially when the rail cant of straight line is 1/20 and that of curve line is 1/40, the wheel-rail shows matching performance. On the condition of measured profile, the concave grinding of wheel tread causes exces-sive equivalent conicity and discontinuous wheel-rail contact points, which can easily lead to abnormal vehicle vibration. And the concave grinding of wheel tread in curve line limits the lateral movement of wheelset. It is difficult for wheel-rail relative motion, which causes poor wheel-rail matching and wheel-rail rolling contact fatigue.

Keyword: metro vehicle; wheel-rail contact; rolling radius difference; equivalent conicity; wheel-rail wear

随着地铁运行速度的提高, 轮轨异常磨耗频发, 出现异常晃车的问题, 轮轨磨耗进一步加剧, 形成恶性循环.通过对地铁列车跟踪测量发现[1, 2]:列车在运营一段时间后车轮踏面发生凹磨, 钢轨表面出现波磨, 轨底坡离散程度大.轨底坡是轨道结构的重要参数, 其对运营地铁轮轨接触特性的影响不容忽视.轨底坡的合理设置, 能够提高列车横向稳定性, 减小轮轨磨耗, 以及减缓轮轨疲劳接触裂纹的产生.

针对轮轨磨耗和轨底坡对轮轨接触特性的影响, 国内外学者开展了大量研究:李艳等[3]通过分析不同磨耗程度下动车组的稳定性、平稳性及安全性指标, 研究了车轮踏面凹磨对列车运行的影响.黄照伟等[4]通过对现场实测车轮踏面轮轨几何接触特性的分析, 研究了车轮踏面凹磨及偏磨对行车性能的不利影响.都敏等[5]通过建立不同轨底坡的车轮和钢轨三维有限元模型, 分析得到增大内轨轨底坡对减缓钢轨侧磨很有效.Sadeghi等[6]从试验和理论两个方面研究了轨底坡对轮轨接触特性的影响, 分析得到轨底坡变化对最大脱轨系数、最大侧向力和平均磨损指数有较大影响.Wang等[7]采用空间接触几何算法和UM软件建模研究了轨底坡对重载铁路轮轨接触状态的影响, 为重载铁路轨底坡取值提供参考.邓建辉等[8]通过l:40轨底坡的铺轨试验, 研究轨底坡和轨头廓面对钢轨接触疲劳伤损的影响.周宇等[9]建立基于临界平面法的钢轨疲劳裂纹萌生寿命预测模型, 研究不同轨底坡对曲线线路钢轨疲劳裂纹萌生寿命的影响.陶功权等[10]通过分析不同轨底坡条件下LM、S1002、DIN5573三种车轮廓形和CHN60钢轨匹配时的行车性能, 寻找最优轨底坡匹配.

可以看出, 现有轮轨接触特性的研究分别着重于不同轮轨廓形匹配时, 最佳轨底坡设置和轮轨磨耗对行车性能的影响, 而缺乏综合考虑轨底坡对磨耗轮轨行车性能影响的研究.因此, 本文作者将通过轮轨接触空间迹线MATLAB程序, 分析轨底坡在实际可能的范围内变化时对磨耗前后轮轨接触几何关系的影响, 同时运用SIMPACK软件建立列车轨道耦合模型, 进行仿真计算, 综合分析线路条件下地铁行车性能, 为解决地铁运营出现的异常晃车、磨耗加剧等问题提供合理建议.

1 计算理论及评价指标
1.1 运营地铁轨底坡及轮轨廓形情况

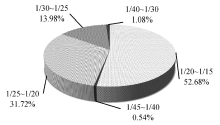
通过对北京某地铁线路进行实地调研, 选取该线路钢轨异常波磨频发、弹条断裂数目较多和异常晃车现象严重区段作为测量段, 对测量段的轨底坡和轮轨廓形进行了测量.图1给出了北京某地铁线路的轨底坡测量数据统计图.由图1可知, 实际线路轨底坡设置离散度很大, 并且大半集中在1/25~1/15范围内, 远远偏离设计值1/40.由图2给出的现场测试图片也可以看出, 钢轨表面波磨、损伤非常明显.

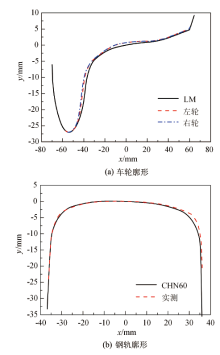
图1 不同轨底坡所占百分比Fig.1 Percentage of different rail cant

图2 现场测试图片Fig.2 Field test pictures

图3给出了LM& CHN60廓形和实测轮轨廓形图像.由图3可知, 在运行一段时间后轮轨都产生了不同程度的磨耗.左右车轮的踏面和轮缘都产生了明显凹磨, 钢轨踏面在磨耗的基础上明显被压扁, 宽度变宽.

图3 轮轨廓形Fig.3 Wheel-rail profile

1.2 轮轨接触空间迹线计算理论

轮轨廓形均由多段圆弧曲线组成, 二者之间的接触关系是空间问题.为简化轮轨接触几何计算过程, 运用解析法建立轮轨空间接触几何的约束方程, 形成一条包含所有可能接触点位置的空间曲线, 并将这条曲线称为“ 空间迹线” [11].

迹线法是通过建立车轮轮轴中心的局部坐标系和轨道中心的整体坐标系, 计算轮轨空间迹线坐标, 寻找左右轮轨垂向距离最小点, 通过侧滚角调整轮对位置, 直至左右轮轨垂向最小距离相等, 确定接触点位置.

1.3 动力学模型建立

选用地铁B型车参数, 应用多体动力学SIMPACK软件建立动力学模型(图4), 对车辆动力学性能进行计算分析.假定模型各结构均为刚体, 车辆运行速度恒定, 仅考虑单节车作用, 不考虑轨枕、轨道板及地基弹性, 轮轨廓形在列车运行过程中不发生变化.定义结构质量、质心坐标及惯性力矩等, 通过施加力元将各结构进行连接.车辆模型由4个轮对、2个转向架和1个车体组成, 每个结构考虑伸缩、横移、沉浮、点头、侧滚、摇头6个自由度, 整个车辆模型共计42个自由度.轮对由一根车轴和两个车轮组成.转向架采用H型焊接构架, 由两侧梁和横梁构成, 轮对与构架通过一系悬挂连接, 二系悬挂则连接构架与车体.车辆模型关于质心中心对称, 一系悬挂、二系悬挂及阻尼都采用线性弹簧.为使计算更合理, 根据Kalker简化滚动接触理论建立轮轨蠕滑力和蠕滑力矩计算模型, 并采用 FASTSIM 算法进行求解.同时, 分别制作了标准LM& CHN60廓形和实测轮轨廓形文件, 导入到模型中, 计算轮轨接触特性.主要车辆参数为:车体质量, 35.24 t; 转向架质量, 2972.77 kg; 轮对质量, 1494 kg; 转向架轴距, 2.3 m; 转向架中心距, 12.6 m; 车轮滚动圆直径, 0.84 m; 滚动圆横向跨距, 1.493 m; 车体长度, 19.52 m; 车体宽度, 2.8 m; 车体高度, 3.8 m.

图4 车辆动力学模型Fig.4 Vehicle dynamics model

1.4 轮轨接触力学评价指标

为更好的反映列车的行车性能, 选取轮轨间磨耗数、最大接触应力和疲劳因子对轮轨磨耗和轮轨表面塑性变形情况进行评估.

轮轨接触斑处的磨耗数可以表示为

W=Txvx+Tyvy+Mzφz(1)

式中: Tx、Ty和 Mz分别为纵向和横向蠕滑力及垂向蠕滑扭矩; vx、vy和 φz分别为纵向和横向蠕滑系数及垂向扭转蠕滑系数.

根据Hertz接触理论, 假定轮轨间为等效弹性接触, 轮轨间最大接触应力可表示为

pmax=3Nel2A(2)

式中: Nel为轮轨接触区域的法向力; A为接触斑面积.

根据安定理论[12, 13], 轮轨表面疲劳因子计算公式为

ε=Tx2+Ty2Nel-2Ak3Nel(3)

式中: k为轮轨材料的剪切屈服强度, 这里取值为300 MPa.疲劳因子大于0时说明进入了材料滚动接触疲劳区, 轮轨接触表面容易形成疲劳接触裂纹.

2 轨底坡对轮轨接触几何的影响

在不同轨底坡条件下, 分别计算横移量变化时LM& CHN60廓形和实测轮轨廓形的接触几何关系, 对比分析轮轨匹配状态.

2.1 轮轨接触位置

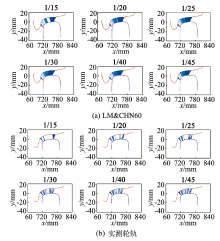
图5给出了轨底坡为1/15、1/20、1/25、1/30、1/40、1/45, 横移量为± 12 mm时LM& CHN60廓形和实测轮轨廓形右侧轮轨接触点位置图像.由图5(a)可知, 轨底坡在1/45~1/20范围内时, LM& CHN60廓形匹配轮轨接触点均匀分布在钢轨轨头工作面上, 当轨底坡增加至1/15时, 接触点逐渐分散, 接触区域内出现分区, 轮轨接触出现不连续.

图5 不同轨底坡条件下轮轨接触点位置Fig.5 Location of wheel-rail contact points under different rail cant

由图5(b)可知, 与LM& CHN60廓形匹配时相比, 在轨底坡为1/30~1/15时, 实测轮轨接触点不连续的情况始终存在, 接触点由接触区域中心向两侧分散, 出现较多分区.尤其是轨底坡在1/25~1/15范围内时, 接触点分布非常集中于某些区域, 这些区域偏向钢轨两侧, 间隔很宽, 跳变区域明显.轨底坡为1/45~1/40时, 轮轨接触点连续性较好.轮轨接触点的不连续说明轮轨匹配不良, 容易引起轮轨之间的冲击和接触振动.

2.2 滚动圆半径差、等效锥度及重力刚度

在轮轨接触几何参数中, 滚动圆半径差和等效锥度是反映轮轨匹配关系的重要指标.滚动圆半径差能够反映横移量变化时接触点的连续性, 等效锥度则能反映横移量变化时接触点沿车轮径向的变化量.滚动圆半径差和等效锥度越大, 轮对恢复对中能力越强, 曲线通过能力也越强, 但过大的滚动圆半径差和等效锥度会降低车辆运行的平稳性, 致使车辆蛇形失稳.重力刚度则能够进一步反映轮对横移量变化时, 左右车轮所受横向力合力对轮对恢复对中位置的作用.因此在分析轮轨接触点位置的基础上, 采用滚动圆半径差、等效锥度和重力刚度衡量轮轨接触特性.

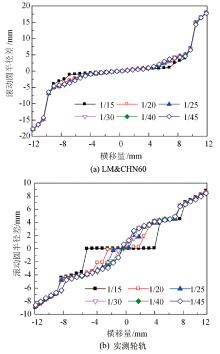
图6给出了轨底坡为1/15、1/20、1/25、1/30、1/40、1/45, 横移量在± 12 mm范围内变化时LM& CHN60廓形和实测轮轨廓形滚动圆半径差图像.由图6(a)可知, 轨底坡为1/45~1/20时, 横移量在9 mm以内时, LM& CHN60廓形滚动圆半径差变化平缓; 横移量超过9 mm时能够提供较大的滚动圆半径差, 保证曲线通过能力.轨底坡为1/15时, 横移量为4~9 mm时, 滚动圆半径差曲线出现明显曲率变化段.说明轨底坡为1/15时, CHN60& LM廓形匹配接触点产生不连续的情况, 接触点分布出现跳变区域.

图6 不同轨底坡条件下滚动圆半径差图像Fig.6 Images of rolling radius difference under different rail cant

由图6(b)可知, 轨底坡为1/25~1/15, 横移量在9 mm以内时, 滚动圆半径差曲线曲率趋近于0, 且分段明显; 横移量大于9 mm时, 实测轮轨滚动圆半径差相较于LM& CHN60廓形滚动圆半径差明显减小.结合图5可知, 实测廓形在轨底坡大于1/25时, 接触点严重分区, 接触不连续情况明显.在横移量较大时实测轮轨接触点没有分布在轮缘上, 而是位于轮缘根部, 导致滚动圆半径差较小.

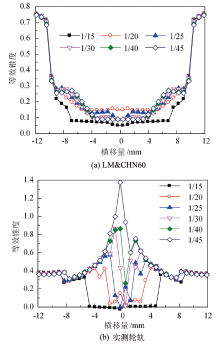
图7给出了轨底坡为1/15、1/20、1/25、1/30、1/40、1/45, 横移量在± 12 mm范围内变化时LM& CHN60廓形和实测轮轨廓形等效锥度图像.由图7(a)可知, 轨底坡为1/45~1/20时, LM& CHN60廓形等效锥度变化规律基本一致.横移量在4~9 mm范围内时, 等效锥度随横移量增大变化较快, 最大值没有超过0.4; 横移量超过9 mm后接触点位于轮缘位置, 等效锥度先急剧增加, 然后又趋近于平缓.

图7 不同轨底坡条件下等效锥度图像Fig.7 Images of equivalent conicity under different rail cant

由图7(b)可知, 与LM& CHN60廓形相比, 实测轮轨在小横移量(2 mm以内)时, 等效锥度在各轨底坡条件下均急剧增加.尤其是在轨底坡为1/45时, 横移量为0.36 mm时的等效锥度已经超过1, 导致列车运行时的横向稳定性受到影响.

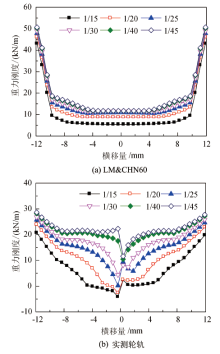
图8给出了轨底坡为1/15、1/20、1/25、1/30、1/40、1/45, 轴重为115.67 kN, 横移量在± 12 mm范围内变化时LM& CHN60廓形和实测轮轨廓形重力刚度图像.由图8(a)可知, 随轨底坡增加, LM& CHN60廓形的重力刚度逐渐减小, 但变化趋势基本相同.当横移量超过9 mm时, 重力刚度在各轨底坡条件下快速增加, 产生了更大的横向复原力, 更有利于轮对自动恢复对中位置.

图8 不同轨底坡条件下重力刚度图像Fig.8 Images of wheelset gravity stiffness under different rail cant

由图8(b)可知, 与LM& CHN60廓形相比, 实测轮轨的重力刚度变化范围明显小于LM& CHN60廓形, 且随着轨底坡减小, 重力刚度变化范围逐渐减小, 轮对自动恢复对中位置能力差.

3 轨底坡对车辆动力学性能的影响

分别建立直线段和曲线段, 分析不同轨底坡条件下地铁列车的行车性能.直线段列车运行速度为100 km/h.曲线段采用正交试验, 综合考虑各种线路参数对车辆动力学性能的影响情况, 曲线超高均为120 mm.规定行进方向左侧的车轮为外轮, 右侧的车轮为内轮.

3.1直线段车辆动力学性能分析

图9给出了直线上轨底坡为1/15、1/20、1/25、1/30、1/40、1/45时, 一位轮轨磨耗数、最大接触应力和疲劳因子图像, 由于直线上左右侧轮轨运行状态基本相同, 因此仅给出一侧对比图像.LM& CHN60廓形在各轨底坡条件下磨耗数均趋近于0, 故在图中没有给出.由图9(a)可知, 与LM& CHN60廓形相比, 实测轮轨一位轮轨磨耗数增加, 在轨底坡为1/20时最大, 但也没有超过0.05N, 因此在直线上车轮凹磨、钢轨波磨以及轨底坡变化对轮轨磨耗的影响不明显.由图9(b)可知, LM& CHN60廓形在轨底坡为1/20时, 直线上最大接触应力最小; 轨底坡为1/45~1/25时, 实测轮轨的最大接触应力小于LM& CHN60廓形.由图9(c)可知, 直线上各轨底坡条件下, LM& CHN60廓形和实测轮轨廓形疲劳因子均小于0, 特别是在轨底坡为1/25~1/20时, 滚动接触疲劳性能良好.

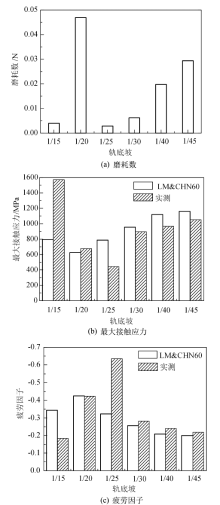图9 直线上不同轨底坡条件下轮轨接触特性Fig.9 Images of wheel-rail contact characteristics under different rail cant on straight line

图10给出了轨底坡为1/45时, 直线上不同速度条件下实测轮轨一位轮轴横向加速度时程图像.由图可知, 轨底坡为1/45, 运行速度为100 km/h时, 实测轮轨一位轮轴横向加速度幅值显著增加, 并且出现周期性振荡, 而速度减小至90 km/h以下时没有出现这种异常振荡现象.说明在轨底坡为1/45, 运行速度增加至100 km/h时, 列车会出现异常晃车, 列车运行稳定性差.

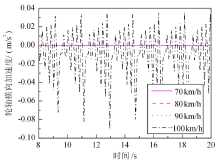图10 轨底坡为1/45时实测轮轨一位轮轴横向加速度时程Fig.10 Time history of lateral acceleration of 1st wheel axle under rail cant of 1/45

根据直线段车辆动力学性能分析可以看出, LM& CHN60廓形在轨底坡为1/20时, 轮轨间最大接触应力小, 不易产生滚动接触疲劳裂纹.直线段实测廓形容易产生异常晃车, 运行稳定性差.

3.2 曲线段车辆动力学性能分析

由于曲线地段曲线半径、车速、轨底坡等参数对车辆动力响应均有影响, 若单独分析, 不仅工作量大, 各因素之间的关系也无法体现.因此设计三因素三水平正交试验, 较为全面地涵盖不同影响因素组合情况[14].为使正交试验更具代表性, 选取各因素水平为:曲线半径300、400、650 m; 车速50、60、65 km/h; 轨底坡1/15、1/20、1/40, 具体如表1所示.

表1 正交设计 Tab.1 Orthogonal design

图11给出了曲线上不同因素水平下一位轮轨磨耗数、最大接触应力和疲劳因子图像.由图11(a)和图11 (b)可知, 曲线半径越小, LM& CHN60廓形和实测廓形内外轮磨耗数均越大.LM& CHN60廓形在各因素水平条件下外轮磨耗数均大于内轮磨耗数; 轨底坡为1/40时, LM& CHN60廓形在各曲线上内轮磨耗数均最小.由图11(c)和图11 (d)可知, 曲线上轨底坡变化对LM& CHN60廓形内外轮最大接触应力影响比较明显, 实测轮轨廓形外轨最大接触应力在各轨底坡条件下基本不变, 但在曲线半径为300 m时急剧增大.由图11(e)和图11 (f)可知, 各因素条件下LM& CHN60廓形内外轨疲劳因子均小于实测轮轨; 在轨底坡为1/40时, 各曲线上LM& CHN60廓形内轮疲劳因子最小, 不容易产生滚动接触疲劳裂纹; LM& CHN60廓形外轨和实测轮轨内外轮疲劳因子均大于0, 容易产生滚动接触疲劳裂纹.轨底坡变化对各曲线上实测轮轨疲劳因子影响不明显.

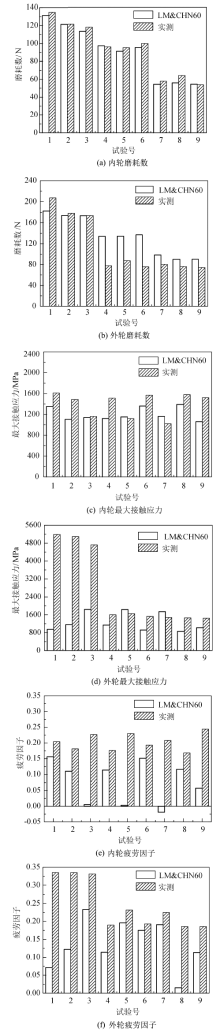图11 曲线上不同因素水平条件下行车性能图像Fig.11 Images of wheel-rail contact characteristics under different factors and levels on curve line

图12给出了缓和曲线与圆曲线过渡段不同因素水平条件下一位轮轴横向加速度时程图像.

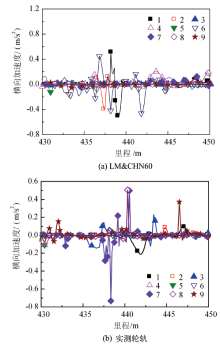图12 圆曲线与缓和曲线过渡段不同因素水平条件下一位轮轴横向加速度时程图像Fig.12 Time history of lateral acceleration of 1st wheel axle under different factors and levels on transition section between transition curve and circular curve

由图12可知, 轨底坡变化对LM& CHN60廓形的轮轴横向加速度影响明显, 轨底坡为1/40时LM& CHN60廓形的轮轴横向加速度波动较小.实测轮轨在各曲线上轮轴横向加速度波动明显, 晃车现象较为严重, 轨底坡变化对实测轮轨横向加速度影响不明显.

根据曲线段车辆动力学性能分析可以看出, LM& CHN60廓形在轨底坡为1/40时磨耗数较小, 最不易产生滚动接触疲劳裂纹.实测廓形由于车轮凹磨限制了轮轨间的相对运动, 轮对对中困难, 轮轨匹配不良, 容易出现异常晃车, 以及产生滚动接触疲劳裂纹.

4 结论

结合某地铁B型车实测型面, 通过采用轮轨接触空间迹线计算方法, 开展了不同轨底坡条件下轮轨接触几何参数分析, 并分析了直线段和曲线段轮轨几何关系对行车性能的影响, 研究得到:

1)LM& CHN60匹配条件下, 轨底坡在1/45~1/20范围内时轮轨接触点连续, 特别是直线段在轨底坡为1/20、曲线段在轨底坡为1/40时轮轨匹配性能良好.

2)地铁实际线路车轮踏面凹磨造成等效锥度过大, 轮轨接触点分布不连续, 列车运行稳定性差; 根据本文算例, 直线段轨底坡为1/45, 列车运行速度为100 km/h时异常晃车现象十分显著.

3)地铁实际线路车轮踏面凹磨限制了轮对横向运动, 重力刚度较小, 导致轮对对中困难, 轮轨廓形匹配不良, 易造成轮轨滚动接触疲劳.

综上所述, 轨底坡对轮轨接触特性影响显著, 但在实际中应综合考虑轨底坡和轮轨廓形对轮轨匹配的影响.对发生磨耗的轮轨廓形应根据不同磨耗情况分区段进行廓形优化设计工作, 根据优化廓形有针对性的进行修理性打磨, 以减少异常晃车和轮轨磨耗加剧的现象发生.

参考文献
[1] 李晓龙, 马卫华, 罗世辉. 踏面下凹磨耗对地铁车辆动力学性能的影响[J]. 内燃机车, 2013(1): 17-20.
LI Xiaolong, MA Weihua, LUO Shihui. Effect of tread concave wear on dynamic performance of metro vehicles[J]. Diesel Locomotives, 2013(1): 17-20. (in Chinese) [本文引用:1]
[2] 李克飞, 刘维宁, 张厚贵, 等. 地铁钢轨波浪形磨耗的研究分析[J]. 都市快轨交通, 2010, 23(2): 1-6.
LI Kefei, LIU Weining, ZHANG Hougui, et al. Study and analysis on rail corrugation on metro lines[J]. Urban Rapid Rail Transit, 2010, 23(2): 1-6. (in Chinese) [本文引用:1]
[3] 李艳, 张卫华, 池茂儒, 等. 车轮踏面外形及轮径差对车辆动力学性能的影响[J]. 铁道学报, 2010, 32(1): 104-108.
LI Yan, ZHANG Weihua, CHI Maoru, et al. Influence of wheel tread profile and rolling diameter difference on dynamic performance of vehicles[J]. Journal of the China Railway Society, 2010, 32(1): 104-108. (in Chinese) [本文引用:1]
[4] 黄照伟, 崔大宾, 杜星, 等. 车轮偏磨对高速列车直线运行性能的影响[J]. 铁道学报, 2013, 35(2): 14-20.
HUANG Zhaowei, CUI Dabin, DU Xing, et al. Influence of deviated wear of wheel on performance of high-speed train running on straight tracks[J]. Journal of the China Railway Society, 2013, 35(2): 14-20. (in Chinese) [本文引用:1]
[5] 都敏, 张军, 王春艳, 等. 城市轨道交通线路轨底坡对钢轨磨耗的影响[J]. 铁道机车与动车, 2014(6): 1-5.
DU Min, ZHANG Jun, WANG Chunyan, et al. Effect of rail cant on rail wear in urban rail transit[J]. Railway Locomotive and Motor Car, 2014(6): 1-5. (in Chinese) [本文引用:1]
[6] SADEGHI J, FATHALI M, BOLOUKIAN N. Development of a new track geometry assessment technique incorporating rail cant factor[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2009, 223(3): 255-263. [本文引用:1]
[7] WANG P, GAO L, HOU B W. Influence of rail cant on wheel-rail contact relationship and dynamic performance in curves for heavy haul railway[J]. Applied Mechanics and Materials, 2013, 365/366: 381-387. [本文引用:1]
[8] 邓建辉, 陈朝阳, 邓勇, 等. 轨底坡和轨头廓面对钢轨接触疲劳伤损的影响研究[J]. 铁道建筑, 2011(8): 109-111.
DENG Jianhui, CHEN Zhaoyang, DENG Yong, et al. Study on the effect of rail cant and rail profile on rail contact fatigue damage[J]. Railway Engineering, 2011(8): 109-111. (in Chinese) [本文引用:1]
[9] 周宇, 王少锋, 张杰, 等. 轨底坡对曲线线路钢轨疲劳裂纹萌生寿命的影响[J]. 中国铁道科学, 2015, 36(1): 25-32.
ZHOU Yu, WANG Shaofeng, ZHANG Jie, et al. Effect of rail cant on fatigue crack initiation life of curve rail[J]. China Railway Science, 2015, 36(1): 25-32. (in Chinese) [本文引用:1]
[10] 陶功权, 温泽峰, 陆文教, 等. 不同轨底坡下地铁车辆轮轨型面匹配的动力学分析[J]. 铁道学报, 2016, 38(5): 16-22.
TAO Gongquan, WEN Zefeng, LU Wenjiao, et al. Dynamic analysis of wheel and rail profile matching relationship for metro vehicle under different rail cant conditions[J]. Journal of the China Railway Society, 2016, 38(5): 16-22. (in Chinese) [本文引用:1]
[11] 唐辰, 陆正刚. 轮轨接触几何分析及其在Maple下的实现[J]. 中国铁道科学, 2011, 32(6): 16-21.
TANG Chen, LU Zhenggang. Analysis of wheel-rail contact geometry and its implementation in Maple[J]. China Railway Science, 2011, 32(6): 16-21. (in Chinese) [本文引用:1]
[12] EKBERG A, KABO E, ANDERSSON H. An engineering model for prediction of rolling contact fatigue of railway wheels[J]. Fatigue & Fracture of Engineering Materials and Structures, 2002, 25(10): 899-909. [本文引用:1]
[13] 韩鹏, 张卫华, 李艳, 等. 轮对磨耗与轮径差对高速列车动力学性能的影响[J]. 交通运输工程学报, 2013, 13(6): 47-53.
HAN Peng, ZHANG Weihua, LI Yan, et al. Influence of wheelset wear and wheel radius difference on dynamics performances of high-speed train[J]. Journal of Traffic and Transportation Engineering, 2013, 13(6): 47-53. (in Chinese) [本文引用:1]
[14] 熊超华, 雷晓燕. 正交试验下地铁诱发的环境振动影响分析[J]. 噪声与振动控制, 2015, 35(1): 169-175.
XIONG Chaohua, LEI Xiaoyan. Influencing factors analysis for environmental vibration induced by subway operations based on orthogonal experiments[J]. Noise and Vibration Control, 2015, 35(1): 169-175. (in Chinese) [本文引用:1]