第一作者:陈广华(1966—),女,天津人,高级工程师,硕士. 研究方向为机械电子工程. email:ghchen1@bjtu.edu.cn.
为了解决热重分析仪器反应迟钝、不能线性控温等问题,提出了一种模糊PID改进算法.首先设计对应的模糊PID控制器来进行温度的控制,其次借助于ANSYS软件建立炉温度场模型,分析得出炉温受加热功率、燃烧物放热等因素的影响.为了能更加精准地进行温度控制,对控制器进行了改进,加入了非线性校正参数αt和燃烧放热补偿参数uq经过Matlab/Simulink仿真实验并与传统的控制器进行对比分析,改进的模糊PID控制器调节时间缩短了19.8 s,超调量减少了0.92,能较为有效地解决热重分析设备反应迟钝、温度非线性等问题.
In order to solve the problems of slow response and non-linear temperature control of thermogravimetric analyzer, an improved fuzzy PID algorithm is proposed. Firstly, the corresponding fuzzy PID controller is designed to control the temperature. Secondly, the temperature field model of the furnace is established by means of ANSYS software. The analysis shows that the furnace temperature is affected by factors such as heating power and heat release of combustion products. In order to control temperature more accurately, the controller is improved by adding non-linear correction parameter αt Through the simulation experiment of Matlab/Simulink and comparing with the traditional controller, the adjusting time of the improved fuzzy PID controller is shortened by 19.8 s and the overshoot is reduced by 0.92, which can effectively solve the problems of slow response and temperature nonlinearity of thermogravimetric analysis equipment.
在整个热分析体系中, 热重分析仪器是进行物质研究非常重要的一个仪器, 它在药物、能源、化工及食品领域都扮演着很重要的角色[1].在材料研究方面, 该仪器相较于其他分析仪器具有功能齐全、体积小等优势, 而且便于进行温度控制.它的装备和材料工程装备有很多相似的地方, 其控温装置和参数测量装置也非常先进.
在对热重分析时, 其中很重要的一个环节是分析不同条件下生物质的相应反应机理, 然而分析是否准确、合理, 会受到多方面因素的影响, 主要包括炉内温度是否达到要求、温度场的实际分布状况、在进行反应时温度的变化情况等.要对加热炉的温控进行优化, 首先必须建立相应的炉温分布模型.建立较为准确的模型并对其进行有效控制存在很大困难, 这是由加热炉自身的一些特性所导致的, 例如大惯性、非线性、不确定性、时滞性等[2].为了预测加热炉的典型动态变化情况, 文献[3]采用三维段法建立了加热炉动态数学模型, 该模型以能量平衡定理及热传导等理论为基础.然而通过该模型预测温度时, 预测值与实际温度间存在着较大的误差, 滞后时间较长, 且控制策略非常复杂.而文献[4]采用了RBF神经网络预测模型进行了炉温控制的仿真, 通过该模型进行预测时, 预测值与实际值之间的误差达到10 ℃, 仍然无法满足现加热过程的相关要求.当前针对炉温度场模型的研究中还未有较全面的数学分析, 同时炉内温度分布影响因素方面的研究也非常少, 还未能建立较为完善的温度场模型.
相较于国内, 国外技术研究的起步较早, 材料方面的研究也更深入、更先进, 如美国、法国、瑞士、韩国等国家都已生产出热重分析仪.这些分析仪的性能较高, 价格不菲, 这些国家的厂商对技术进行了严格的控制与保密, 国内很难对其进行深入研究与改进.我国对温控系统的研究起步较晚, 各种常规的或是经过改进的PID占据了主导地位.文献[5]创建的电加热炉温控系统是以单神经元PID为基础的, 该系统受环境变化等因素的影响较小, 充分体现了PID控制算法的优点, 并能够有效地改进线性时变对象的动态品质.文献[6]基于混合型模糊PID控制建立了加热炉温控系统, 根据温度偏差值的大小来切换PID控制或者模糊控制.通过试验可知, 应用该类控制虽然比传统的PID控制能够有效提高温度的控制精度和响应速度, 减少能耗, 但仍不能满足更高的精度要求.在热重分析设备方面, 尽管国内展开了一定的研究并在实际中有相应的应用, 然而与国外相比, 我国在应用智能控制技术方面非常落后, 以ZRT-B型热重分析仪(由北京精仪高科研制)为例, 尽管其能够满足一定实际需求, 但是其自身还存在多方面的不足, 包括智能化程度相对较低、分辨率低及未能实现小型化等.
对材料研究的设备来讲, 保证机器在各种温度条件及内部环境下都可以高精度的工作是非常重要的.由于温度很容易受到燃烧产物、工作功率以及气流等非线性的影响[7], 不适合采用传统的控制算法, 主要原因是这种算法要借助于公式进行计算, 有较高的精度要求.如果被控对象及系统等都较为简单, 可以适用这类算法; 如果被控对象具有一定的时变性、滞后性且相对复杂, 这种温控系统就难以满足实际需要.相比之下, 模糊PID控制算法主要依赖于设备的实际工作经验, 可以降低未知因素对设备带来的影响.所以, 不管是从理论研究还是实际应用, 都应基于现有的温控技术而设计一款智能化程度更高、扩展性更强、小型化且造价低的热重分析设备.
本文作者分析了煤以及典型生物质燃料, 得出影响温度的主要因素, 并针对研究结果提出了模糊PID的改进算法, 其使用效果优于传统的PID算法, 使得热重分析仪器能够在各种工作条件下正常运行.此外, 研究结果为分析生物质燃烧特征提供了有效途径, 有助于实现对生物质资源的有效利用.
热重分析仪器在进行传热的过程中是对多个非线性产量进行整合的过程, 它需要更为精确的温度控制, 是工业生产中非常重要的一类仪器.在进行加热的过程中, 首先根据使用者的设置来确定升温速率(变温控制)以及温度(恒温控制).因为影响温度的因素过多, 所以变温控制依然存在很多问题, 而恒温控制运行起来问题较少.当系统接收到升温信号后, 为了保证温度在1~2 ℃的范围内波动, 所以对设备的稳定性要求非常高; 另外温度变化的区间为0~850 ℃, 温度的变化范围很大, 所以热重分析设备的滞后性以及非线性问题对其运行具有较大影响; 此外, 燃料的发热和其他很多因素都会影响设备正常运作.
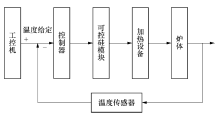
图1所示的是根据控温要求完成的加热炉控温系统.其输入信号为设备温度, 借助温度传感器得到电炉内的温度作为反馈信息; 利用温度控制算法, 控制器计算得到控制量, 最后输出在0~5 V的范围内的电压信号; 可控硅模块接收电压调节的信号, 改变加热功率, 从而调节炉内的温度.
首先, 结合模糊控制器与PID控制器二者的优点设计出模糊PID控制器.为了能更加精准地进行温度控制, 运用有限元分析[8, 9]方法建立模型, 研究得出影响炉温的关键因素后, 在模糊PID控制器的基础上进行算法改进.
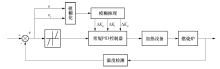
构成整个模糊PID控制器的结构组份主要有:传统PID控制器与模糊推理参数校正.图2是模糊PID控制器的结构示意图.
PID控制器经过参数调整后, PID控制器根据输入的内部参数对温度进行控制.“ 两入三出” 模式是模糊控制器主要的运行模式.根据系统内的温度变化和实际需要对温度控制区域进行调整后确定模糊语言变量的论域.当温度在0~850 ℃时, 整个温度升高的速率范围大致是0~0.5 ℃/s.因为在具体过程中温度变化缓慢但范围较大, 所以在系统误差小于± 15 ℃时采用模糊PID控制器进行温度控制, 大于这个误差值即可全功率进行加热.表1列出了模糊语言变量的论域.
| 表1 模糊语言变量的论域 Tab.1 Fuzzy linguistic variables |
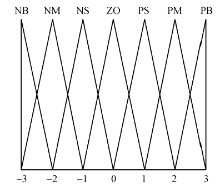
为了保证控制器的精确度并简化计算过程, 输出、输入变量的隶属度函数可遵循图3.
综合考虑系统内部的控制精度以及动态变化特性等因素, 可以根据
| 表2 Δ Kp模糊控制规则 Tab.2 Δ Kp fuzzy control rules |
| 表3 Δ Ki模糊控制规则表 Tab.3 Δ Ki fuzzy control rules |
| 表4 Δ Kd模糊控制规则 Tab.4 Δ Kd fuzzy control rules |
建立相应的温度场模型要对加热炉的温控算法进行优化, 对加热炉模型温度特性进行分析, 从而使后续的加热炉的温度控制改进算法有理可依.
2.2.1 加热炉模型温度特性分析
用ANSYS软件根据热重分析系统中预热炉以及燃烧炉的大小来构建三维立体模型, 使用SOLID90类型, 3D热实体单元[10].其中有加热装置、进气以及出气口等, 图4为加热炉的几何模型.设置初始环境的温度为25 ℃, 利用热生成率类型进行温度载荷的施加, 加热元件温度不得超过1 298 K.
搭建模型后, 采用有限元的分析方法, 通过建立模型来模拟加热炉实际工作情况, 对物料点温度、物料燃烧放热进行分析.
1)物料点温度的瞬态分析.
物料位置温度与炉内加热器的功率有着紧密联系, 随着功率不断增大, 温度也会随之升高, 表5是初始温度为50 ℃、250 ℃、450 ℃、650 ℃下不同加热功率的温度变化速率.
| 表5 不同功率下模型温度上升速率 Tab.5 Rate of rise in model temperature at different powers℃/min |
由表5可以看出, 当功率一定时, 高温时的温度上升速率减慢, 炉内系统与外界环境的热能交换加快.初始温度不断改变时, 热量交换效率也随之改变.要想达到更好的控温效果, 就必须根据加热的温度变化来改变加热器的功率.
2)物料燃烧放热分析.
物料燃烧过程中, 温度随系统内热量的增加而升高[11].随着温度的不断上升, 系统内温度在达到燃点后会开始放热, 进而改变炉内温度.这一燃点区间大概在380 ℃至470 ℃之间, 其中影响物料燃烧放热的主要有物料质量、物料材质以及混合比例3个关键因素.在相同功率下, 分别在450 ℃和400 ℃的初始温度条件下对质量不同的生物质进行加热, 得到的物料位置温度变化如图5所示.
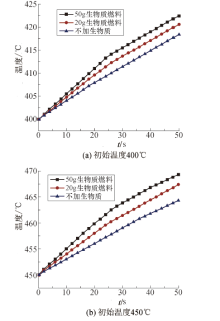 | 图5 不同初始温度时物料位置温度上升曲线Fig.5 Material position temperature rise curve under different initial temperature |
在生物质进入加热炉开始燃烧后, 释放热量, 导致温度突然升高, 其温度上升区间取决于所加入生物质的质量, 二者之间为正比关系.控温过程中必须要考虑到物料燃烧放热这一影响因素, 要及时进行温度补偿, 不然会影响到整个加热炉的工作.
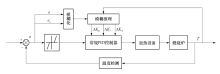
2.2.2 模糊PID控制器的改进算法
在分析物料加热功率、物料燃烧放热等影响因素后, 对现有模糊PID控制器的算法进行改进, 改进后的算法能适应不同环境变化下温度控制参数的计算[12].
1)非线性校正.
当炉内加热物质不同时, 其温度变化规律也会有所不同, 为了解决这一问题, 改进算法中将温度
为了进行非线性影响因素的修正, 需设置校正参数
| 表6 模糊控制规则 Tab.6 Rules of fuzzy control |
比例系数
模糊PID控制器输出增量为
加入了校正参数后的控制器可以适应外界与炉内进行热交换时的温度控制, 控制器的精确度大大提升.
2)燃烧放热因素预估.
燃烧放热对物料加热时的温度影响很大, 所以如何判断并校正物料放热对炉内温度的影响是改进算法需要解决的问题.为了解决这一问题, 引入了补偿参数
物料的质量一般在0~100 g之间, 通过模拟实验计算得到
其比例系数
为了简便
改进算法后的模糊PID控制器最终输出为
通过在可视化软件中对传统PID控制器、模糊PID控制器、改进后的模糊PID控制器三者进行对比分析后, 可以清晰地看出其中的的优劣.
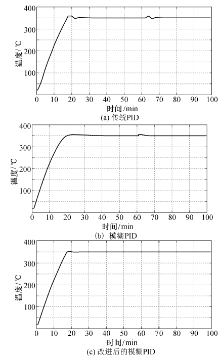
1)传统PID控制器仿真结果.
设采样时间
图7清晰地反映出传统的PID控制器反应较慢, 在温度突变时调节时间
2)模糊PID控制器仿真结果.
偏差e和偏差变化率$e_c$是为提升控制器准确度而引入的参数, 模糊PID控制器在给定输入
由图8可得, 调节时间虽然比传统PID控制器长,
3)改进的模糊PID控制器仿真结果.
在模糊PID控制器的基础上加入校正参数
由图9可得, 在给定值为350 ℃时, 改进后的控制器在温度突变时的响应时间
为了检验3种控制器在存在干扰条件时的工作能力, 在保证加热炉控制模型不变的情况下, 实验60 min时加入了值为15的阶跃干扰信号, 实验具体结果见图10.
在干扰条件加入后, 传统PID控制器的响应时间较长, 且伴随一定的振荡; 模糊PID控制器响应时间比传统PID控制器稍快, 无振荡, 逐渐平稳在温度设定值; 而改进后的模糊PID控制器反应迅速, 在3 min内就排除了干扰, 并且快速地稳定在了温度设定值.
为了避免热重分析炉温度受加热功率、燃烧物放热的影响, 提出了模糊PID控制器的改进算法, 加入了非线性校正参数
1)在给定温度时, 改进后的模糊PID控制器在温度突变时的响应时间
2)系统斜坡响应过程中, 改进后的模糊PID控制器响应在180 s后基本稳定, 稳态过程振荡小, 温度控制精度在± 2 ℃以内, 基本克服了加热功率、燃烧放热等扰动带来的影响.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|