基于卷积神经网络的机票低价预测

引用本文

林友芳, 蒋鹏, 郭晟楠, 武志昊. 基于卷积神经网络的机票低价预测[J]. 北京交通大学学报, 2019,43(5): 1-9.
LIN Youfang, JIANG Peng, GUO Shengnan, WU Zhihao. Air ticket low-price prediction based on convolution neural network[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2019,43(5): 1-9.
Doi:10.11860/j.issn.1673-0291.20180137 复制到剪切板

Permissions

北京交通大学学报编辑部所有

基于卷积神经网络的机票低价预测

林友芳^1,², 蒋鹏¹, 郭晟楠¹, 武志昊^1,²

1.北京交通大学计算机与信息技术学院,北京 100044

2.民航旅客服务智能化应用技术重点实验室,北京 101318

通信作者:武志昊(1984—),男,山西大同人,副教授,博士,博士生导师.email:zhwu@bjtu.edu.cn.

第一作者:林友芳(1971—),男,福建龙岩人,教授,博士,博士生导师.研究方向为网络科学与智能系统.email:yflin@bjtu.edu.cn.

收稿日期: 2018-09-25

基金: 中央高校基本科研业务费专项资金(2019JBM023); 国家自然科学基金(61603028)

摘要

准确的机票低价预测有助于民航需求与供给的灵活对接及民航资源的充分利用.机票价格波动性大、随机性强、易受到诸多因素的影响,使得机票价格预测成为了一个极具挑战的问题.充分考虑机票价格自身特点,设计了二维“机票价格时间片”结构,并基于时间片充分挖掘、利用机票价格数据的规律与关系,设计了以卷积神经网络为核心的两阶段机票价格预测模型,对未来机票最低价格进行预测.在某在线订票网站的真实价格数据集上进行了验证,并与4种流行的基准模型进行了对比.结果表明:本文的方法明显优于其他模型,MAE效果提升了13.67%,MAPE数值降低了1.52%.

关键词: 深度学习; 机票低价预测; 卷积神经网络; 价格序列

中图分类号:TP183 文献标志码:A 文章编号:1673-0291(2019)05-0001-09

Air ticket low-price prediction based on convolution neural network

LIN Youfang^1,², JIANG Peng¹, GUO Shengnan¹, WU Zhihao^1,²

1. School of Computer and Information Technology,Beijing Jiaotong University,Beijing 100044, China

2. CAAC Key Lab of Intelligent Passenger Service of Civil Aviation, Beijing 101318, China

Fund:Fundamental Research Funds for the Central Universities(2019JBM023); National Natural Science Foundation of China (61603028)

Abstract

Accurate low-price air ticket forecasting facilitates the flexible docking of civil aviation demand and supply.It also helps to achieve full utilization of civil aviation resources.Fluctuations of ticket price are large,random,and vulnerable to many factors,making ticket price forecasting a challenging issue.This paper fully considers the characteristics of the ticket price,and designs a two-dimensional “air ticket price time slice” structure.Based on the time slice,the law and relationship of ticket price data can be futher exploited.Besides,the core two-stage ticket price forecasting model is proposed to predict the lowest price of future tickets based on convolutional neural network.Experiments are conducted on the real price dataset of an online booking website and compared with four popular benchmark models.The results show that the proposed method is obviously better than other models.MAE and MAPE achieve improvements of 13.67% and 1.52% respectively.

Keyword: deep learning; low price forecast of airfare; convolution neural network; price sequence

文章图片

近年来, 随着我国民航业自主定价政策的逐步放开, 航空公司对其航班产品的定价越来越自由, 从而使得机票价格制定策略越来越灵活且多元化, 航空公司都会制定出复杂的定价策略以保证其收益最大化.在此背景下, 准确的机票每日最低价格预测(简称价格预测)能够给予普通乘客购买时机的建议从而帮助其买到相对较低价格的机票, 也能够帮助机票代理商适时调整票价以提高民航资源利用率.准确的机票价格预测能够使民航业各方参与者获得更多的反映市场动态的信息, 有助于民航业供应与需求的灵活对接, 从而使民航资源得以更高效、更充分的利用.

航空公司往往会根据航班实际上座情况及旅客需求热度动态调整机票价格, 而这些信息是外部无法获得的.能够获取到的影响因素信息十分有限, 而且机票价格自身波动性大、随机性强, 诸多因素使得机票价格预测成为了一个很具挑战性的问题.目前机票价格预测领域的研究主要分为针对机票价格升高或降低趋势的分类预测问题^[1]和针对具体机票价格数值的预测问题两个方面^{[2, 3, 4]}.前者只能预测价格变动的趋势, 无法准确地知道未来机票价格的数值, 而预测未来具体价格数值的研究方向能够通过预测具体的价格数值更为直观、详细地展现未来票价变化趋势, 更好地对机票价格变动情况进行分析.

针对机票价格数值的预测问题主要存在两大类方法.第一类是基于价格序列自身历史值的时间序列方法.文献[3]基于时间序列的方法设计了结合权重滑动平均和相似时间平均法的综合模型对机票价格数据进行预测, 均方根误差(RMSE)优于指数平滑等传统时间序列方法.文献[4]基于模糊理论构建了机票价格预测的模糊时间序列模型, 在预测准确度上有了一定提升.第二类是针对价格影响因素建立模型的回归方法, 文献[1]结合规则学习、强化学习和时间序列的方法提出了一种集成学习二元分类算法以判断机票价格的升降.文献[2]针对影响机票价格的因素设计了8维特征并利用多种机器学习算法对机票价格进行预测, 并对各算法的准确率和效率进行了对比.

与此同时, 各国学者进行了很多关于卷积神经网络(Convolution Neural Network, CNN)^{[5, 6, 7]}在各领域应用的研究.文献[8]基于CNN设计了两阶段图像补全网络, 针对不完整图片首先使用简单的网络填补出简略的结果, 再利用精细化网络填补出最终结果.文献[9, 10, 11, 12]利用Inception结构设计了GoogLeNet网络以及之后的各个改进版本, 采用多尺度卷积处理, 在增加网络深度和宽度的同时优化网络质量.文献[13]将时空数据与深度学习结合起来, 利用时空深度残差网络解决城市人口流动预测问题.卷积神经网络以其优秀的信息提取及特征表达的能力, 在各个领域都能有所应用.

为了找到适合机票价格预测问题的解决方案, 对数据特点进行了统计分析, 使用采集到的某订票网站的真实价格数据集, 通过数据分析发现机票价格数据存在着单条序列无明显周期性、临近起飞日期对应序列差异性大、连续多个航班序列以“ 星期” 为周期规律性强等特点.针对传统模型仅利用到单条价格序列信息, 无法很好地完成机票价格预测问题.本文作者提出了机票价格时间片的概念与构建方式, 使用连续多个航班最低价格序列构建二维的机票价格时间片以充分利用机票价格各个维度的特点, 基于该时间片以卷积神经网络为核心构建了两阶段机票价格预测模型, 并加入了影响机票价格的时间、城市、航空公司等多方面外部因素的影响, 充分挖掘和利用了机票价格相关的各方面信息, 使预测准确率较之传统方法取得了大幅提升.

1 问题定义

在民航领域, 航班号由航空公司、航线、起飞时间共同确定, 每一个航班号代表的是一个航班产品集, 每个航班号在各个起飞日期对应的某一产品则为具体“ 航班” .例如, “ 航班号” CA1831, 代表的是中国国际航空公司每天上午7:30出发的从北京到上海的所有航班的集合; 而2016年9月6日起飞的航班号为CA1831的航班产品则为某一具体“ 航班” .以下涉及的相关概念给出形式化定义并对所研究的问题进行形式化描述.

定义1 机票最低价格:由于航班产品的特殊性, 每个机票价格存在起飞日期和查询日期两个维度, 针对某航班号确定的对象, 设query_date(简称q)为查询日期, flight_date(简称 $f$ )为起飞日期, 在日期 $q$ 当天查询到的日期 $f$ 起飞的某具体航班的最低价格表示为 $P_{q, f} .$

定义2 机票最低价格序列:针对某个起飞日期确定的具体航班, 起飞前n天每天都会存在一个当天的最低价格, 从而组成一条该航班的最低价格序列.设f为该航班的起飞日期, 则起飞日期f所对应的从前n天到起飞前m天的最低价格序列为

$\begin{array}{l} L_{f}^{n, m} = {P_{f - n, f - m}, P_{f - (n - 1), f - m}, \dots, P_{f - (m + 1), f - m}, P_{f - m, f - m}} \end{array}$ (1)

定义3 起飞日期所属最低价格时间片:不同起飞日期的具体航班同属于一个航班号所确定的产品集, 每个航班对应一条定义2所确定的价格序列, 从这一系列价格序列中取连续k个起飞日期对应的k条价格序列, 每条序列长度为n, 构建成n× k矩阵的形式即可得到本文定义的机票价格时间片.则构建f所属时间片的形式化定义为

$\begin{array}{l} S^{f - (k - 1), f} = {L_{f - (k - 1)}^{n, 0}, L_{f - (k - 2)}^{n, 0}, \dots, L_{f - 1}^{n, 0}, L_{f}^{n, 0}} \end{array}$ (2)

如图1所示, 构造的 $n \times k$ 大小的矩阵, 即为后续模型中涉及的价格时间片, 其中每个网格代表相应位置的价格.

	Figure Option View Download New Window
	图1 机票价格时间片设计Fig.1 Design of ticket price time slice

问题定义:基于上述定义, 本文所研究的机票价格预测问题可描述为:针对某航班号确定的对象, 已知过去k天每天起飞的该航班产品各自起飞前n天的机票每日最低价格和未来k天每天起飞的该航班产品各自起飞前n天至当前日期已产生的价格, 预测未来k天每天还未产生的价格, 共计[k(k+1)]/2个值.用定义3中的时间片表示完全已知的已起飞k个起飞日期航班对应价格时间片为

$\begin{array}{l} S_{this}^{f - (k - 1), f} = {L_{f - (k - 1)}^{n, 0}, L_{f - (k - 2)}^{n, 0}, \dots, L_{f - 1}^{n, 0}, L_{f}^{n, 0}} \end{array}$ (3)

未来 $k$ 个起飞日期航班对应价格时间片的已知部分为

$S_{next_1}^{f + 1, f + k} = {L_{f + 1}^{n, 1}, L_{f + 2}^{n, 2}, \dots, L_{f + (k - 1)}^{n, k - 1}, L_{f + k}^{n, k}}$ (4)

需要预测的未知部分的值

$S_{next_2}^{f + 1, f + k} = {L_{f + 1}^{0, 0}, L_{f + 2}^{1, 0}, \dots, L_{f + (k - 1)}^{k - 2, 0}, L_{f + k}^{k - 1, 0}}$ (5)

由此, 在当前日期f构建如图2所示的两个k维时间片, 按定义3描述:时间片1即为日期f所属的时间片, 其中所有值都已知; 时间片2为日期f+k所属的时间片, 其中白色网格为已知部分, 黑色网格为未知部分, 即需要预测的目标.

	Figure Option View Download New Window
	图2 机票低价预测问题输入双时间片设计Fig.2 Design of double time slice for ticket price prediction problem

2 模型与算法

本节提出了以卷积神经网络为核心的两阶段机票价格预测模型见图3, 模型第1阶段用简单预测方法填补时间片未知部分, 从而构造完整时间片作为后续模型输入; 第2阶段利用多形状卷积神经网络对时间片进行特征提取, 并结合多维外部特征利用多层全连接网络对最终结果进行精细化预测.图3中第1阶段this时间片和next时间片即为问题定义中提到的时间片1和2; 第2阶段, Conv 1~6为不同形状的卷积层, Dense为全连接神经网络层, Output即为最终输出.

	Figure Option View Download New Window
	图3 两阶段模型整体架构Fig.3 Overall framework of the two stage model

2.1 机票价格时间片构造与简单预测

传统的针对机票价格预测问题的模型^[14], 都是以固定起飞日期的单条价格序列作为其核心研究对象.这类研究方式只考虑了某一起飞日期对应航班产品的特点, 极少地利用到与其临近的起飞日期以及周期性同类产品的价格信息.基于上述分析, 本文充分考虑航班产品存在起飞日期、查询日期两个序列维度的特点, 针对性地设计了机票价格时间片结构.

2.1.1 价格时间片构造

本文模型的输入为两个相邻的时间片, 由定义3, 第1个时间片为当前日期所属时间片, 第2个时间片是当前日期后第 $k$ 天所属的时间片.第1个时间片包含了近期k个已起飞所有航班的数据, 第2个时间片包含了要预测的k个起飞日期已知的价格数据以及要进行预测的未发生的价格数据.时间片的设计将机票价格数据组织成了类似图像的网格数据形式, 所以在处理第2个时间片空缺未知数据时, 借鉴了图像修复领域两阶段图像修复模型^[8]的思想.模型的第1阶段使用简单的预测方法对时间片的空缺值进行预测并填充, 第2阶段基于之前构造的两个时间片进行精确预测.

2.1.2 简单预测

本文的简单预测方法是三阶滑动平均法, 针对第2个时间片的每条序列, 利用其各自已有价格数据对未知项进行预测.滑动平均法是一种利用近期历史数据对未来进行预测的常用方法, 能够利用近期数据的特点并消除随机波动, 而且算法简单、计算量小, 很适合用以完成第1阶段简单预测的任务.

2.2 DC_Airfare网络与精确预测

基于第1阶段构建好的两个时间片输入, 模型的第2阶段以卷积神经网络为核心设计了精细化的预测模型, 模型整体架构如图4所示.

2.2.1 时间片特征提取

时间片的设计形式上类似于图像, 但与图像有着较大差别.时间片横向序列提供了航班自身随着起飞日期临近价格变动规律的信息, 纵向序列提供了相同查询起飞间隔的各航班价格的周期性规律信息.与图像局部特征更丰富的特点不同, 时间片在横纵两个方向上的特征更为明显且更为重要.并且时间片的数据点数远小于正常图像的数据点数.

基于上述时间片特点分析, 时间片特征提取网络的设计遵循了如下思想:使用多个不同形状的卷积神经网络提取时间片中行列两个方向维度的特征, 同时降低网络深度并适当利用dropout操作以减少网络参数.如图4所示, 针对每一个时间片输入, 首先使用BatchNormalization层^[15]做数据的标准化, 以加快训练速度, 提高模型精度, 然后分别使用卷积核形状为1× 3, 3× 1, 1× 5, 5× 1, 3× 3的5个卷积层(Conv2D)提取第1层特征, 接着做最大池化(MaxPooling)操作, 再分别做3× 3的卷积操作、接池化操作和dropout操作, 之后将结果“ 压平” 成 $n$ 维向量, 用一个全连接层调整结果向量的大小.每个时间片经过5个不同形状的特征提取网络的操作后, 都会得到5组不同维度的特征向量.本模型两个时间片作为输入, 则最终得到10组特征向量.

	Figure Option View Download New Window
	图4 DC_Airfare网络结构Fig.4 Network structure of DC_Airfare

2.2.2 外部特征引入

机票价格不仅自身存在规律, 同时还受到很多外部因素的影响, 如航空公司因素、航线因素、航班时间相关因素等多方面的有价值信息.所以, 本模型综合考虑了表1所列的外部因素特征信息.

表1 外部因素设计 Tab.1 External factor design

2.3 算法与优化

算法1概括描述了DC_Airfare模型的训练过程.第1~8行介绍了将原始数据构建成模型所需输入实例的过程, 10~14行介绍了模型反向传播和Adam优化器进行训练的过程, 其中损失函数为平均绝对误差MeanAbsoluteError.

算法1 DC_Airfare训练算法

Input: 历史价格数据: ${L_{f - (k - 1)}^{n, 0}, L_{f - (k - 2)}^{n, 1}, \dots, L_{f + (k - 1)}^{n, k - 1}, L_{f + k}^{n, k}}$

外部特征: $\{E_{0}, E_{1}, \dots, E_{n - 1}, E_{n}\}$

Output:训练完成的DC_Airfare模型

//构建训练实例

1 $D$ ← ∅;

2 for 出发日期 $f (1 \leq f$ ≤ End) do{

3 $S_{this}^{f - (k - 1), f} = \{L_{f - (k - 1)}^{n, 0}, L_{f - (k - 2)}^{n, 0}, \dots, L_{f - 1}^{n, 0}, L_{f}^{n, 0}\}$

4 $S_{next_1}^{f + 1, f + k} = \{L_{f + 1}^{n, 1}, L_{f + 2}^{n, 2}, \dots, L_{f + (k - 1)}^{n, k - 1}, L_{f + k}^{n, k}\}$

5 $Feature = \{E_{0}, E_{1}, \dots, E_{n - 1}, E_{n}\}$

6 $S_{next_2}^{f + 1, f + k} = \{L_{f + 1}^{0, 0}, L_{f + 2}^{1, 0}, \dots, L_{f + (k - 1)}^{k - 2, 0}, L_{f + k}^{k - 1, 0}\}$

7 构建训练实例 $(\{S_{this}, S_{next}, Feature\}, S_{pre}), 存入 D;}$

8 //模型训练

9 初始化模型参数θ ;

10 do{

11 从 $D$ 中随机选出一批训练实例 $D_{batch}$ ;

12 用 $D_{batch}$ 训练模型以最小化MeanAbsoluteError , 并更新 $θ;$

13 }until (满足所有终止条件)

3 实验结果与分析

在真实的价格数据集上进行了实验, 将本文提出的方法与其他4种基本的方法进行对比.

3.1 实验数据

本文使用的数据来自国内某订票网站爬取的真实数据集, 包含了涉及32条航线、11家航空公司的共计428个航班的数据, 每个航班记录了连续46个起飞日期(2016/10/09— 2016/11/23)涉及到的日最低价格数据, 其中每个起飞日期对应起飞前历史40 d查询价格值.

图5为航班号为CA1831的同一周(2016/10/31— 2016/11/06)内不同日期起飞的7个具体航班对应的7条价格序列曲线.可以看出针对某一航班号所确定的航班产品, 各个起飞日期对应的价格序列无明显周期性, 大部分航班前期较平稳甚至连续多点不变, 后续有整体升高趋势并且波动较大, 而且同一周内起飞的各航班产品的价格曲线模式存在较大差异.将同一航班号各个起飞日期对应的价格序列根据起飞日期顺序排列首尾相接, 得到图6.

	Figure Option View Download New Window
	图5 CA1831航班同周内各起飞日期对应价格数据曲线Fig.5 CA1831 flights correspond to price data curves for each departure date in the same week

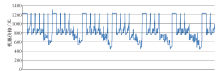	Figure Option View Download New Window
	图6 CA1831连续46 d起飞价格序列首尾相接示意图Fig.6 CA1831 multiple consecutive 46 d take-off dates for price sequence

可以看出, 相同航班号不同日期起飞的航班中, 以星期为整体进行观察发现各周期之间的价格模式很相似, 存在着很强的规律性.基于上述数据特点分析, 最终确定的机票价格时间片形状为40× 7(即取 $n = 40, k = 7)$ , 即每个时间片包含同一航班号连续7个起飞日期的价格序列, 每条序列包含起飞前40 d的价格信息.

3.2 对比方法及评价指标

3.2.1 对比方法

如前所述, 在机票价格预测领域主要有两种解决思路:1)基于自身价格序列的变动发展规律使用时间序列的方法去解决; 2)利用外部因素设计特征采用回归的方法解决.对数据进行分析之后, 发现机票价格数据存在着不适合采用时间序列方法解决的特点.首先, 针对某个航班的机票价格不同于其他商品可以无限延伸下去的价格序列, 某具体航班的价格序列会随着航班的起飞而终止; 其次, 机票价格序列呈现上文提到的特点:前期能够利用的数据变动较小, 甚至连续多个点无波动, 而临近起飞日期价格波动剧烈, 前后数据无明显周期性、规律性.由此, 时间序列预测方法难以很好地解决此问题.最终本文选择更适合解决此问题的回归模型作为对比方法.

本文采用4种回归方法作为对比模型.

1)贝叶斯岭回归(Bayesian Ridge, BR), 贝叶斯岭回归结合了贝叶斯回归和岭回归特点的回归方法, 主要解决在最大似然估计中很难决定模型的复杂程度的问题.

2)弹性网络回归(Elastic Net, EN):弹性网络是一种使用 L1, L2范数作为先验正则项训练的线性回归模型.这种组合允许学习到一个只有少量参数是非零稀疏的模型.

3)线性回归(Linear Regression, LR):线性回归是利用数理统计中的回归分析, 来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法, 运用十分广泛.

4)梯度提升回归(GBR):梯度提升回归是一种从其自身训练过程的错误中进行学习的技术.本质上就是集思广益, 集成一堆较差的学习算法进行学习.

针对上述回归方法, 利用已知数据及相关信息从航班的时间信息、地理信息、近期数据特点、周期性数据特点等多方面设计了如表2所示共计62维特征.

表2 回归模型特征 Tab.2 Characteristics of regression model

属性类别	详细描述	类型	维数
时间属性	查询日期星期属性	one-hot编码	7
	起飞日期星期属性	one-hot编码	7
	查询起飞间隔	one-hot编码	7
	起飞时间段	one-hot编码	4
	降落时间段	one-hot编码	4
	是否跨天	布尔值	1
地理属性	出发城市等级	布尔值	1
	到达城市等级	布尔值	1
	航线长度	Double	1
	航空公司标识	one-hot编码	11
统计信息	价格序列前 $k$ 个值的均值	Double	1
	价格序列前 $k$ 个值的方差	Double	1
	起飞日期之前7 d各自的均值	Double	7
	起飞日期之前7 d各自的方差	Double	7
	历史查询起飞间隔相同的7 d的均值	Double	1
	趋势性系数	Double	1

表2 回归模型特征 Tab.2 Characteristics of regression model

3.2.2 评价指标

本文使用平均绝对误差(MAE)和平均绝对百分比误差(MAPE)两种指标评价模型的预测性能.

MAE计算公式为

$M_{AE} = \frac{1}{n} \sum_{i = 1} | f_{i} - y_{i} |$ (6)

式中: $f_{i}$ 表示预测值, $y_{i}$ 表示真实值.

MAPE计算公式为

$M_{APE} = \frac{1}{n} \sum_{i = 1} \frac{|f_{i} - y_{i}|}{y_{i}} \times 100 %$ (7)

3.3 实验设置与结果分析

3.3.1 实验设置

本文在模型训练实验过程中的参数设置如下:优化函数optimizer为Adam优化函数, 损失函数loss为MeanAbsoluteError, 采用早停(EarlyStopping)策略进行训练, 训练停止限制patience设置为2, 训练最大轮数epoch为2 500.迭代2 500轮训练过程未自动停止, 模型损失loss的变化情况如图7所示.可以看出训练前期存在波动, 2 000轮之后损失趋于稳定, 所以最终设置训练轮数epoch为2 000.

	Figure Option View Download New Window
	图7 模型loss变化Fig.7 Change of model loss

3.3.2 实验结果分析

在真实的价格数据集上实验并与基本模型进行对比, 表3给出了本模型与4种对比模型进行总体预测实验时在测试集上MAE和MAPE的结果, 同时也给出了模型自身只利用时间片而未加入外部因素时的实验效果.从表3中可以看到, 所有对比模型中, ElasticNet的效果最差, GBR效果最好, 其他两种对比模型性能相当, 但是都有较大的误差.本文的模型不仅得到了最好的结果, 而且相对于次好的GBR模型, MAE降低了16.61, 有13.67%的性能提升, MAPE降低了1.52%.而本模型如果不加入外部因素、只利用时间片结构进行预测, 实验效果比完整模型稍差但优于对比模型, 可以看出外部因素对模型预测效果起到了提升作用.

表3 总体预测实验结果对比 Tab.3 Comparisons of overall prediction

图8给出了DC_Airfare模型与4种对比方法在未来一周内每天的MAE与MAPE的对比结果.可以看出随着预测天数的增加, 各个模型的MAE和MAPE指标都有所变差, 而DC_Airfare模型在各天的预测效果均优于其他模型.该实验结果表明, 本文提出的模型能够较好解决未来机票价格预测问题.

	Figure Option View Download New Window
	图8 5种模型逐天预测效果对比Fig.8 Comparisons of 5 models for predicting daily effects

4 结论

针对机票价格预测问题, 考虑到机票价格数据存在起飞日期和查询日期两个维度的特殊性, 创新性地设计了能够充分融合机票价格信息的时间片结构, 并针对此结构设计了基于卷积神经网络的两阶段预测模型.

1)在真实数据集上对提出的模型进行实验, 并且与4种流行的预测方法进行了对比, 取得了很好的预测效果.提出的模型通过为民航业各方参与者提供反映市场动态的信息, 能够为购票者和机票代理商提供准确有效的决策支持, 有助于民航业供应与需求的灵活对接, 从而使民航资源得以更高效、更充分的利用, 具有很高的实用价值.

2)提出的时间片构建及预测模型设计方法, 为有相同特点的航班需求、航班查询量等民航领域其他预测问题提供了新的思路.

本文的模型相比其他几种方法取得了较好的预测效果, 但是与真实值依然存在一定的差距.为此, 将进一步分析挖掘民航数据的特点, 改进模型, 以提升模型的预测能力.

参考文献

文献列表

[1]	ETZIONI O, TUCHINDA R, KNOBLOCK C A, et al. To buy or not to buy: mining airfare data to minimize ticket purchase price[C]//Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2003: 119-128. [本文引用:2]
[2]	TZIRIDIS K, KALAMPOKAS T, PAPAKOSTAS G A, et al. Airfare prices prediction using machine learning techniques[C]//Signal Processing Conference, 2017: 1036-1039. [本文引用:2]
[3]	ZHENG X, NIU K, MAA J, et al. A prediction algorithm for airfare based on time series[C]//Proceedings of the 7th International Conference on Computer Engineering and Networks, 2017: 1-7. [本文引用:2]
[4]	华逸群, 曹健. 机票价格预测的模糊时间序列方法[J]. 小型微型计算机系统, 2016, 37(11): 2547-2551. HUA Yiqun, CAO Jian. Airfare forecast based on fuzzy time series[J]. Journal of Chinese Computer Systems, 2016, 37(11): 2547-2551. (in Chinese) [本文引用:2]
[5]	林友芳, 尹康, 党毅, 等. 基于时空LSTM的OD客运需求预测[J]. 北京交通大学学报, 2019, 43(1): 114-121. LIN Youfang, YIN Kang, DANG Yi, et al. Spatio-temporal LSTM for OD passenger demand prediction[J]. Journal of Beijing Jiaotong University, 2019, 43(1): 114-121. (in Chinese) [本文引用:1]
[6]	LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324. [本文引用:1]
[7]	KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classification with deep convolutional neural networks[C]//Advances in Neural Information Processing Systems, 2012: 1097-1105. [本文引用:1]
[8]	YU J, LIN Z, YANG J, et al. Generative image inpainting with contextual attention[J]. arXiv Preprint, 2018. [本文引用:2]
[9]	SZEGEDY C, LIU W, JIA Y, et al. Going deeper with convolutions[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015: 1-9. [本文引用:1]
[10]	IOFFE S, SZEGEDY C. Batch normalization: Accelerating deep network training by reducing internal covariate shift[J]. arXiv preprint arXiv: 1502. 03167, 2015. [本文引用:1]
[11]	SZEGEDY C, VANHOUCKE V, IOFFE S, et al. Rethinking the inception architecture for computer vision[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016: 2818-2826. [本文引用:1]
[12]	SZEGEDY C, IOFFE S, VANHOUCKE V, et al. Inception-v4, inception-resnet and the impact of residual connections on learning[C]//Association for the Advance of Artificial Intelligence, 2017: 4278-4284. [本文引用:1]
[13]	ZHANG J, ZHENG Y, QI D. Deep spatio-temporal residual networks for citywide crowd flows prediction[C]//Association for the Advance of Artificial Intelligence, 2017: 1655-1661. [本文引用:1]
[14]	KINGMA D P, BA J. Adam: A method for stochastic optimization[J]. arXiv preprint arXiv: 1412. 6980, 2014. [本文引用:1]
[15]	IOFFE S, SZEGEDY C. Batch normalization: Accelerating deep network training by reducing internal covariate shift[J]. arXiv preprint arXiv: 1502. 03167, 2015. [本文引用:1]

2003

0.0

... 目前机票价格预测领域的研究主要分为针对机票价格升高或降低趋势的分类预测问题^[1]和针对具体机票价格数值的预测问题两个方面^[2,3,4] ...

... 第二类是针对价格影响因素建立模型的回归方法,文献[1]结合规则学习、强化学习和时间序列的方法提出了一种集成学习二元分类算法以判断机票价格的升降 ...

2017

0.0

... 目前机票价格预测领域的研究主要分为针对机票价格升高或降低趋势的分类预测问题^[1]和针对具体机票价格数值的预测问题两个方面^[2,3,4] ...

... 文献[2]针对影响机票价格的因素设计了8维特征并利用多种机器学习算法对机票价格进行预测,并对各算法的准确率和效率进行了对比 ...

2017

0.0

... 目前机票价格预测领域的研究主要分为针对机票价格升高或降低趋势的分类预测问题^[1]和针对具体机票价格数值的预测问题两个方面^[2,3,4] ...

... 文献[3]基于时间序列的方法设计了结合权重滑动平均和相似时间平均法的综合模型对机票价格数据进行预测,均方根误差(RMSE)优于指数平滑等传统时间序列方法 ...

2016

0.0

华逸群, 曹健. 机票价格预测的模糊时间序列方法[J]. 小型微型计算机系统, 2016, 37(11): 2547-2551.

HUA

Yiqun

, CAO

Jian

. Airfare forecast based on fuzzy time series[J]. Journal of Chinese Computer Systems, 2016, 37(11): 2547-2551. (in Chinese)

Airline ticket purchasing is convenient with the development of Internet,and airfare forecast can help passengers or travel agents explore the market and make sophisticated decisions.However,airline companies are using complicated strategies,Being effected by multiple dynamically factors,the real-time price of tickets changes rapidly and has the properties of tendency,randomness and large floating,so we can′t find out an accurate relationship between the history and the future.In this paper,we proposed an airfare forecast model based on fuzzy time series.We analyze the lowest price of 36 airlines from October 2014 to April 2015 and use MAPE as the indicator of prediction results.A comparison was made with three classical time series algorithms：AR,moving average and exponential smoothing,and prove that the model of fuzzy time series can increase the accuracy of the forecast,especially when the price changes significantly and the performance of each line are less floating.As a result,airfare forecast can provide passengers a pretty reliable decision support.

（Department of Computer Science an Engineering,Shanghai Jiaotong University,Shanghai 200240,China）

网络使得机票预订更加便捷,机票价格预测可以帮助旅客、代理商合理的选择购买时间、了解市场.然而各航空公司定价机制复杂,机票实时价格受多方面因素影响不断变化,具有趋势性、随机性和波动性的特点,历史价格与预测值间很难用精确的关系表示.文中将模糊时间序列引入机票价格预测问题中,利用36条航线的最低价格数据（201410—20154）进行预测,并用绝对平均误差对实验结果进行评估.将预测结果与传统的时间序列AR模型、移动平均和指数平滑比较,结果表明模糊时间序列模型可以提高预测的准确率,不同航线的预测误差结果浮动较小,且在价格波动较大时准确率有明显提升,并提供较可靠的购票决策支持.

... 目前机票价格预测领域的研究主要分为针对机票价格升高或降低趋势的分类预测问题^[1]和针对具体机票价格数值的预测问题两个方面^[2,3,4] ...

... 文献[4]基于模糊理论构建了机票价格预测的模糊时间序列模型,在预测准确度上有了一定提升 ...

2019

0.0

... 与此同时,各国学者进行了很多关于卷积神经网络(Convolution Neural Network,CNN)^[5,6,7]在各领域应用的研究 ...

1998

0.0

... 与此同时,各国学者进行了很多关于卷积神经网络(Convolution Neural Network,CNN)^[5,6,7]在各领域应用的研究 ...

2012

0.0

... 与此同时,各国学者进行了很多关于卷积神经网络(Convolution Neural Network,CNN)^[5,6,7]在各领域应用的研究 ...

2018

0.0

... 文献[8]基于CNN设计了两阶段图像补全网络,针对不完整图片首先使用简单的网络填补出简略的结果,再利用精细化网络填补出最终结果 ...

... 时间片的设计将机票价格数据组织成了类似图像的网格数据形式,所以在处理第2个时间片空缺未知数据时,借鉴了图像修复领域两阶段图像修复模型^[8]的思想 ...

2015

0.0

... 文献[9,10,11,12]利用Inception结构设计了GoogLeNet网络以及之后的各个改进版本,采用多尺度卷积处理,在增加网络深度和宽度的同时优化网络质量 ...

2015

0.0

... 文献[9,10,11,12]利用Inception结构设计了GoogLeNet网络以及之后的各个改进版本,采用多尺度卷积处理,在增加网络深度和宽度的同时优化网络质量 ...

2016

0.0

... 文献[9,10,11,12]利用Inception结构设计了GoogLeNet网络以及之后的各个改进版本,采用多尺度卷积处理,在增加网络深度和宽度的同时优化网络质量 ...

2017

0.0

... 文献[9,10,11,12]利用Inception结构设计了GoogLeNet网络以及之后的各个改进版本,采用多尺度卷积处理,在增加网络深度和宽度的同时优化网络质量 ...

2017

0.0

... 文献[13]将时空数据与深度学习结合起来,利用时空深度残差网络解决城市人口流动预测问题 ...

2014

0.0

... 1 机票价格时间片构造与简单预测传统的针对机票价格预测问题的模型^[14],都是以固定起飞日期的单条价格序列作为其核心研究对象 ...

2015

0.0

... 如图4所示,针对每一个时间片输入,首先使用BatchNormalization层^[15]做数据的标准化,以加快训练速度,提高模型精度,然后分别使用卷积核形状为1#cod#x000D7 ...