藏式古建结构动力响应计算中人群荷载参数敏感性分析

引用本文

杨娜, 戴璐. 藏式古建结构动力响应计算中人群荷载参数敏感性分析[J]. 北京交通大学学报, 2019,43(4): 71-79.
YANG Na, DAI Lu. Sensitivity analysis of crowd load parameters in Tibetan heritage structural dynamic response calculation[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2019,43(4): 71-79.
Doi:10.11860/j.issn.1673-0291.20180147 复制到剪切板

Permissions

北京交通大学学报编辑部所有

藏式古建结构动力响应计算中人群荷载参数敏感性分析

杨娜¹, 戴璐^1,²

1.北京交通大学土木建筑工程学院,北京 100044

2.北京林业大学材料科学与技术学院,北京 100083

第一作者:杨娜(1974—),女,辽宁大连人,教授,博士,博士生导师.研究方向为古建结构监测.email:nyang@bjtu.edu.cn.

收稿日期: 2018-10-11

基金: 国家自然科学基金(51778045,51878034); 中央高校基本科研业务费专项资金(BLX201719)

摘要

古建结构的游客荷载是结构分析中重要的荷载形式.人群荷载形式复杂且由多个参数控制,影响结构响应的人群荷载参数包括行人数量、行人质量、行人步频等.为确定上述参数对结构响应的影响程度,从概率分析的角度出发,结合人群荷载作用下结构加速度响应的频谱计算方法,探究一种结构响应对人群荷载参数敏感性的分析方法.首先将人群荷载参数看作随机变量,其次利用典型藏式古建木构的现场调研数据来获得人群参数的分布规律,最后采用所提出的敏感性分析方法来计算结构响应在人群荷载参数波动范围内敏感性系数的变化规律,结果表明:在各个参数发生相同程度的波动时,相比行人质量和行人数量,步频对结构响应的影响最为显著.

关键词: 人群荷载; 敏感性; 加速度; 步频; 质量; 行人数量

中图分类号:TU366.2 文献标志码:A 文章编号:1673-0291(2019)04-0071-09

Sensitivity analysis of crowd load parameters in Tibetan heritage structural dynamic response calculation

YANG Na¹, DAI Lu^1,²

1. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044,China

2. College of Materials Science and Technology, Beijing Forestry University, Beijing 100083,China

Fund:National Natural Science Foundation of China(51778045,51878034); Fundamental Research Funds for the Central Universities(BLX201719)

Abstract

Tourist load is an important load form in the structural dynamic analysis of heritage building, which is a complex load form influenced by multiple factors including the number of pedestrians, the average weight and the stride frequency. In order to figure out the influence of the parameters above on crowd load parameter, based on the statistical theory and the calculation method of structural acceleration spectral density function, this paper proposes asensitivity analysis strategy for the structural response to crowd load. The crowd load parameters are taken as random variables, the distribution and changing rules of the parameters are obtained from field investigation in the typical Tibetan heritage building. The varying trend of the sensitivity factor of the crowd load parameters can be obtained from the analysis, the results show that compared with the number of pedestrians and the average weight, stride frequency has the largest influence on the structure response when the fluctuation of these parameters is at the same level. A simply supported beam bridge is taken as an example to verify the feasibility of the proposed method by calculating the sensitivity factor of different stride frequencies.

Keyword: crowd load; sensitivity; acceleration; stride frequency; weight; number of pedestrians

文章图片

随着旅游业的发展, 古建筑中接纳越来越多的游客, 人群激励下结构响应控制变得尤为重要.人群荷载的各个参数不仅具有较强的不确定性, 而且对结构响应的影响程度不同, 因此分析人群荷载参数的敏感性对古建结构响应控制非常重要.

在人致荷载模拟中, 单人荷载通常采用傅里叶级数模型^[1], 而在考虑人群效应时, 通常采用 $\sqrt[]{N}$ 倍的单人荷载^[2]作为作用在结构上的人群荷载, 其中N为行人数量.简方梁等^[3]通过有限元模拟, 分析了不同人群荷载排列工况下结构响应的特征; 高延安等^[4]采用质量-弹簧模型, 对人群中人与人之间的相互作用进行了详细的分析.

此外, 许多学者已经对参数敏感性分析做过相关研究, 其中最常见的模型是多元线性回归模型, 而基于拉丁几何取样的多元回归方法、傅里叶敏感性检验法、利用非参数统计方法进行敏感性分析的方法、Morris法、方差分解法等, 都是目前常用的敏感性分析方法^{[5, 6, 7, 8, 9]}.近年来, 一些学者将人工神经网络技术应用到参数分析敏感性分析中, 以提高计算效率.目前基于神经网络技术的参数敏感性分析法中主要有Garson法、随机化检验法、PaD2法^{[10, 11, 12]}.然而, 由于操作困难, 这类方法仍停留在理论研究阶段, 难以解决工程实际问题.应用较为广泛的参数敏感性分析方法是基于概率理论开展的^[13], 它具有理论清晰、操作便捷等优点.目前, 对于敏感性指标尚无统一的标准, 常用的评价准则有基于可靠度一次二阶矩方法的无量纲敏感性指标^[14]、重要性敏感性指标、失效概率对随机变量均值敏感性指标、失效概率对方差敏感性指标^[15]等.

为研究结构响应对人群荷载参数的敏感性问题, 探究各个参数对响应的影响程度, 更好地对古建结构的振动进行控制.本文作者对藏式古建木结构的构造特征与动力特性进行分析, 基于参数敏感性的概率理论, 并结合人群作用下结构响应的谱分析法^[16], 提出一种结构响应对人群荷载参数敏感性的分析方法.将该方法应用到典型的藏式古建木结构中, 获得了人群荷载参数的敏感性系数在自身波动范围内的变化规律.研究表明, 相比行人质量和数量, 结构响应对行人的步频更为敏感, 在人群荷载参数发生相同程度的波动时, 结构加速响应受行人步频的影响最大.

1 藏式古建木结构

1.1 结构构造特征

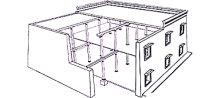
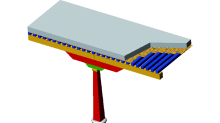
藏式木结构古建筑的结构体系与传统的汉式建筑的结构体系有着显著的不同.藏式建筑属密梁平顶式结构(见图1), 是传统木构架结合了西藏地区特色之后应用发展起来的, 具有自身的特点, 与传统木构体系的最大区别在于墙体和木构架共同承重, 外观则表现为厚墙、窄窗、平屋顶.藏式建筑中每个单体为一个独立的结构单元, 平面内部按井字形(或近似井字形)布置若干上下贯通的墙体.墙体内部则是木构架体系, 通常用梁柱组成纵向排架, 梁上铺密椽; 若需加大内部空间, 则设置数列纵排架.建筑各层的梁柱排架上下对齐, 一般不使用通柱.藏式古建筑楼面系统与木梁连接紧密, 楼面的做法为梁上密铺椽子, 椽上密铺直径6~8 cm的圆木、半圆木(曲面向下)或木板作承重层, 也称为占棍.占棍上铺一层直径小于10 cm的卵石或碎石.在卵石层上铺约10 cm厚的黏土垫层.待垫层稍干, 上铺一层厚约15 cm的阿嘎土作为面层, 楼面的构造如图2所示.厚重的墙体及楼盖系统使得藏式建筑有着较大的抗侧刚度和竖向刚度.

	Figure Option View Download New Window
	图1 密梁平顶式结构Fig.1 Typical Tibetan building structure

	Figure Option View Download New Window
	图2 藏式古建楼板构造Fig.2 Structure of Tibetan wooden structure

1.2 结构动力特性

人群荷载作用下的结构响应分析属于动力响应分析的范畴, 因此在明确结构的构造之后, 需要分析结构动力特性.

本文获取结构动力特性参数的方法为现场实测.由于测试目的是获得结构本身的参数, 因此激励形式选择不会额外增加结构质量的环境激励, 并且测试在夜间无游客时进行, 以保证结构中无其他外激励.为保证足够的数据量, 根据误差估计计算, 每种工况的测试时长为30 min, 采样频率为512 Hz.在测试中, 采集的数据为各个测点处的加速度响应, 传感器为电荷输入式加速度传感器(扬州科动KD1300), 可测试某个位置处单一方向的加速度响应, 每个传感器位置配套使用一个电荷放大器(扬州科动KD5002).为保证测试数据的可靠性, 将传感器吸附在较重的支座上.

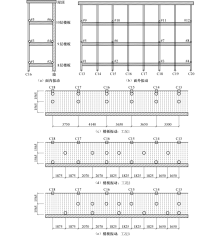
为获得结构木框架在面内、面外以及楼板的竖向振动特征, 共设计了5种测试工况.如图3所示.

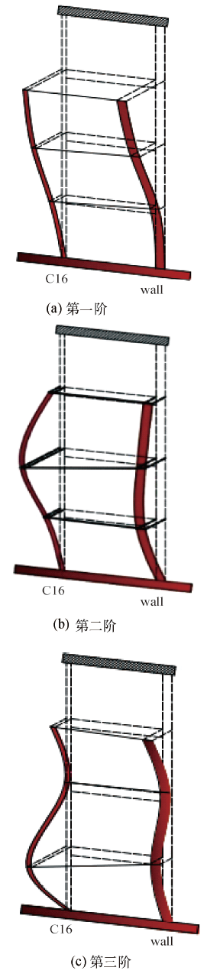
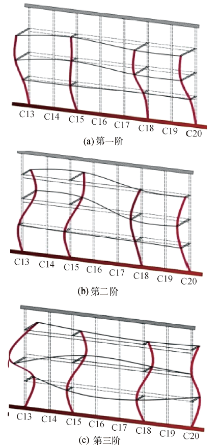
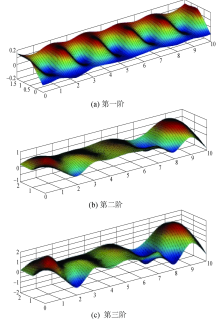
	Figure Option View Download New Window
	图3 结构动力特性测试测点布置(单位:mm)Fig.3 Sensor placements(unit:mm)

采集得到各个测点布置处的加速度位移响应后, 采用时域内的模态参数识别方法随机子空间法, 对结构面内、面外振动以及楼板竖向振动的动力特性进行了分析.计算获得了结构各个部分前三阶模态参数, 包括模态频率、振型和阻尼比, 具体计算结果如表1所示, 振型分布如图4~6所示.

表1 结构振动模态参数计算结果 Tab.1 Parameters in vibration modes of the structure

	Figure Option View Download New Window
	图4 框架面内振动振型Fig.4 In-plane vibration mode

	Figure Option View Download New Window
	图5 框架面外振动振型Fig.5 Out-of-plane vibration mode

	Figure Option View Download New Window
	图6 楼板竖向振动振型Fig. 6 Vertical vibration mode

通过分析, 获得了典型藏式古建回廊部分木构框架面内、面外振动的前三阶模态频率、阻尼比和振型.结果表明, 木构框架面外振动的自振频率较低, 说明此方向刚度较小.同时, 面外振动的一阶振型呈现弯曲型特征, 而面内振动一阶振型则呈现剪切型特征, 同样说明木构框架的面外刚度小、面内刚度大.

通过楼板振动测试, 获得了藏式古建楼板竖向振动的前三阶模态频率、振型和阻尼比.楼板一阶振型在各跨呈现出了规律的支座处不动、跨中下沉的特征; 在二阶和三阶振型中, 这一特征表现得更加明显.

2 参数敏感性分析

2.1 基于概率的参数敏感性分析方法

在对上述藏式古建木结构进行人群荷载参数敏感性分析时, 选用了基于概率的参数敏感性分析方法, 其具体理论如下:

假设随机变量Y是参数X=(x₁, x₂, …, x_n)的函数, Y=g(x₁, x₂, …, x_n), 则当参数X发生波动Δ =(D₁, D₂, …, D_n)时, 变量Y的波动可表示为

$Y^{'} = Y + Δ Y = g (X + Δ)$ (1)

在X=(x₁, x₂, …, x_n)处对式(1)进行泰勒展开, 有

$\begin{array}{l} g (x_{1} + D_{1}, x_{2} + D_{2}, ..., x_{n} + D_{n}) = \\ g (x_{1}, x_{2}, ..., x_{n}) + \overset{n}{\sum_{i = 1}} a_{i} D_{i} + \\ \overset{n}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} b_{ij} D_{i} D_{j} + R_{n} (X) \sum \\ \begin{array}{l} a_{i} = {\frac{d g}{d x_{i}}|}_{i = 1, 2, ..., n} \\ {b_{ij} = \frac{d^{2} g}{d x_{i} d x_{j}}|}_{i, j = 1, 2, ..., n} \end{array} \end{array}$ (2)

式中, R_n(X)∑ 为泰勒展开余项, 是可忽略的高阶小量.则Δ Y的数学期望可表示为

$\begin{array}{l} E (Δ Y) = \overset{n}{\sum_{i = 1}} E (a_{i}) E (D_{i}) + \\ \overset{n}{\sum_{j = 1}} E (b_{ji}) E (D_{j}^{2}) + \overset{n}{\sum_{i = 1}} \overset{n}{\sum_{j = 1, j \neq i}} E (b_{ij}) E (D_{i} D_{j}) \end{array}$ (3)

式中, 前两项可表示当x_i发生波动D_i时, Y随之波动的敏感程度.

当x_i和x_j分别发生波动D_i和D_j时, 对Y影响程度的比值(即Y对x_i和x_j敏感程度的比值)为

$R_{i / j} = \frac{E (a_{i}) E (D_{i}) + E (b_{ii}) E (D_{i}^{2})}{E (a_{j}) E (D_{j}) + E (b_{jj}) E (D_{j}^{2})}, i \neq j$ (4)

当自变量与因变量有明确的关系, 并且不考虑x_i与x_j的相关关系时, 式(4)可以用来计算因变量对自变量敏感程度的比值.当参数多于两个时, 可选取某一参数作为参考, 对敏感性比值进行归一化处理, 从而获得全部参数敏感程度比值.

2.2 结构加速的响应功率谱计算方法

在明确了参数敏感性分析方法后, 如果要根据概率的参数敏感性分析方法进行人群荷载参数分析, 必须要建立施加在结构上的人群荷载与结构响应之间的关系.在此, 选用频域内的人群荷载作用下结构加速度响应功率谱计算方法来建立荷载与响应之间的关系.

单个行人作用在结构上, 其动力荷载系数产生的自功率谱密度函数可表示为

$S_{L} (\frac{f}{\overset{̅}{f}}) = \frac{L^{2} (\frac{f}{\overset{̅}{f}})}{2 d \bar{f}}$ (5)

式中:L为行人行走状态下的动力荷载系数; f为行人步频; $\bar{f}$ 为行人步频的数学期望, $\bar{d f}$ = $\overset{̅}{f}$ /64.

质量为W、平均步频为 ${\bar{f}}_{i}$ 的单个行人i, 其荷载自功率谱密度函数可表示为

$S_{F} (f) = {[WL ({\bar{f}}_{i})]}^{2} S_{L} (\frac{f}{{\bar{f}}_{i}})$ (6)

对N个行人来说, 当行人的平均质量为 $\bar{W}$ 、步频范围为 ${\bar{f}}_{1}$ ~ ${\bar{f}}_{2}$ 时, 总的荷载自功率谱密度可表示为

$S_{P} (f) = N \int_{{\bar{f}}_{1}}^{{\bar{f}}_{2}} {[\bar{W} L (\bar{f})]}^{2} \cdot S_{L} (\frac{f}{\overset{̅}{f}}) \cdot φ (\bar{f}) d \bar{f}$ (7)

式中:S_P $(f)$ 为荷载自功率谱密度; φ $(\bar{f})$ 为行人步频分布的概率密度函数; L $(\bar{f})$ 为以 $\bar{f}$ 为变量的动力荷载系数函数.

由于步频为正态分布, 则 $\int_{{\bar{f}}_{1}}^{{\bar{f}}_{2}}$ S_L $(\frac{f}{\overset{̅}{f}}) \bar{d f}$ =0.5, 因此式(7)可写为

$S_{P} (f) = N {\bar{W}}^{2} φ (f) \cdot L^{2} (f) / 2$ (8)

由上述分析可知, 具有步频分布φ $(f)$ 、行人平均质量 $\bar{W}$ 、人数为N的人群荷载产生的功率谱密度函数可根据式(8)计算获得.

结构响应的功率谱密度函数可表示为

$S_{a} (f) = {|H (f_{n})|}^{2} S_{P} (f)$ (9)

式中:H(f_n)为结构的频响函数; f_n为结构随人群荷载作用的振动频率.

3 人群荷载参数分布

在参数敏感性分析中, 需要考虑参数的分布与波动规律, 对人群荷载来说, 主要考虑的参数包括行人数量、行人步频和行人质量.结合现有的研究基础和现场调研, 对这3个参数的分布形式进行分析.

由于本研究是针对藏式古建木结构开展的, 因此通过对第1节介绍的典型藏式古建木构中的游客行走特征进行现场调研, 对人群荷载的参数分布特征进行了统计分析.

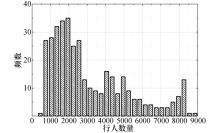
统计该藏式古建结构中一年内参观游客的数量, 可以获得行人数量的分布特征, 每天的游客数量分布形式如图7所示.

	Figure Option View Download New Window
	图7 行人数量分布Fig.7 Distribution of pedestrian number

把结构中的游客数量作为行人数量这一人群荷载参数, 并且把天作为基本统计单元.由计算可得, 行人数量的日均值 $\bar{N}$ =3 145, 方差S_N=2 118, 变异系数V_N=0.67.

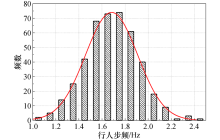
在游客行走特征测试中, 采取跟踪记录的方法, 测试者在游客不知情的情况下观察或跟踪游客行走, 记录其通过标定距离所用的时间(秒表记录)和所需步数, 统计400个样本的测试数据, 可获得游客通过标定距离的步频分布, 如图8所示.

	Figure Option View Download New Window
	图8 行人步频分布Fig.8 Distribution of stridefrequency

由图8可知, 行人步频呈现明显的正态分布.统计其特征参数, 可知行人步频服从均值为1.68 Hz、方差为0.442的正态分布, 即f~N(1.68, 0.44²).

行人体重分布来源于2014年国民体质监测公报^[17].由监测公报公布的数据可知, 中国20~59岁成年人体重分布服从均值为62.8 kg、方差为10.9的正态分布, 即W~N(62.8, 10.9).

4 荷载参数敏感性

将基于概率的参数敏感性分析方法结合人群荷载作用下结构加速度响应谱计算方法, 并采用游客行走参数分布特征, 探究一种针对藏式古建木结构的人群荷载参数敏感性分析方法.

4.1 分析方法

在分析中, 考虑3个人群荷载参数, 分别为x₁(行人数量N)、x₂( 行人体重W)、x₃(步频f).当3个变量分别发生百分比为k的波动时, 分析结构响应对不同参数的敏感性.在此需要说明的是, 人群荷载参数的波动量指的是不同变量数学期望的波动值, 方差并不发生变化.

人致荷载选用傅里叶级数模型, 各阶动力荷载系数为:D₁=0.37, D₂=0.10, D₃=0.12, D₄=0.04, D₅=0.08, 这里选用的动力荷载系数与步频无关, 有

$\{\begin{array}{l} Y = x_{1} {|H (f)|}^{2} {\bar{W}}^{2} φ (f) \cdot L^{2} (f) / 2 \\ Y = x_{2}^{2} {|H (f)|}^{2} Nφ (f) \cdot L^{2} (f) / 2 \\ Y = {|H (f_{n})|}^{2} {\bar{W}}^{2} Nφ (x_{3}) \cdot L^{2} (x_{3}) / 2 \end{array}$ (10)

式中:H(f)为结构的频响函数; $\bar{W}$ 为行人平均质量; N为行人数量; φ $(f)$ 为行人步频分布的概率密度函数; L为动力荷载系数函数.

将作用在结构上的人群荷载参数看作自变量, 结构响应看作因变量, 则当自变量发生波动k时, 根据式(2), 分别计算敏感性计算公式(4)中的系数a_i和b_ii, 即可获得响应对各个参数波动的敏感性比值.

在工程实践中, 由于常通过减少行人数量控制人致振动, 因此首先将行人质量与行人步频对结构响应的影响程度与行人数量对比, 有如下结果:

对行人数量和质量来说, 将计算系数代入式(4)中, 可获得结构响应对行人数量和质量的敏感性比值, 有

$R_{1 / 2} = \frac{k}{2 k + 2 k^{2} + \frac{2 S (W)}{{\bar{W}}^{2}}}$ (11)

式中:k表示参数波动百分比; $\bar{W}$ 表示行人质量均值; S(W)表示行人质量分布方差.

对行人数量和步频来说, 将各计算系数代入式(4)中, 可获得结构响应对行人数量和步频的敏感性比值, 有

$\begin{array}{l} R_{\frac{1}{3}} = \\ \frac{k}{2 k μ_{f} (f - μ_{f}) + (2 - \frac{2}{σ_{f}^{2}} {(f - μ_{f})}^{2}) ({(k μ_{f})}^{2} + S (f))} \end{array}$ (12)

式中:k表示参数波动百分比; μ _f表示行人步频均值; σ _f表示行人步频分布的标准差.

整理式(11)和式(12)可知, 当参数都发生百分比为k的波动时, 结构响应对上述3个参数的敏感性之比可表示为

$\begin{array}{l} R_{1 : 2 : 3} = k : (\begin{array}{l} 2 k + 2 k^{2} + \\ \frac{2 S (W)}{{\bar{W}}^{2}} \end{array}) : \\ (\begin{array}{l} 2 k μ_{f} (f - μ_{f}) + \\ [2 - \frac{2}{σ_{f}^{2}} {(f - μ_{f})}^{2}] [{(k μ_{f})}^{2} + S (f)] \end{array}) \end{array}$ (13)

4.2 分析结果

应用上述分析结果, 分别计算结构响应对行人数量、行人质量以及行人步频敏感程度的比值.

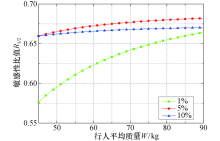
根据式(11), 可以获得当人群荷载参数发生不同程度波动(即波动量k取不同值)时, 结构响应对行人数量和行人平均质量敏感性程度的比值, 如图9所示.

	Figure Option View Download New Window
	图9 行人数量与质量对结构响应影响程度比值Fig.9 Ratio between the influence of pedestrian number and weight

在图9中, 横坐标表示行人平均质量, 纵坐标表示行人数量和质量对结构响应影响程度的比值, 可以看出:

1)从敏感性比值来看, 在发生不同程度的参数波动时, 结构响应对行人数量和质量的敏感性比值最大为0.68, 最小值为0.58.可见, 行人平均质量的波动对结构响应的影响较大, 约为行人数量发生同样百分比波动的1.5~2倍.

2)相比行人数量, 行人质量对结构响应的影响随平均质量的增加而减弱.也就是说, 当行人数量一定时, 结构响应对平均质量较小的行人群体的质量波动更为敏感.

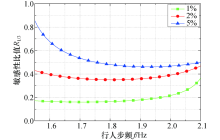
根据式(12), 可以获得当参数发生不同程度波动时, 结构响应对行人数量和步频敏感性程度的比值.当行人步频发生波动较大时, 其步频超出正常行走的步频范围, 不符合实际情况, 因此只计算步频波动较小时对结构响应的影响, 结果如图10所示.

	Figure Option View Download New Window
	图10 行人数量和步频对结构响应影响程度比值Fig.10 Ratio between the influence of pedestrian number and stride frequency

在图10中, 横坐标表示行人步频, 纵坐标表示行人数量和行人步频对结构响应影响程度的比值, 可以看出:

1)从敏感性比值来看, 在发生不同程度的参数波动时, 结构响应对行人数量和步频的敏感性比值最大为0.9, 最小值为0.18.可见, 行人平均步频的波动对结构响应的影响较大, 约为行人数量发生同样百分比波动的1.1~5倍.

2)相比行人数量的影响, 步频对结构响应的影响随着参数波动的增大而减弱.行人步频对结构响应影响范围很大, 同时也说明控制行人步频对结构响应的控制范围更大.

由以上分析可知, 结构响应对行人数量的波动最不敏感, 因此下面着重分析行人质量和步频对结构响应的影响.

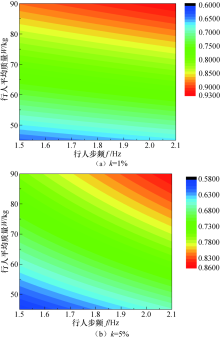
由式(13)可知, 行人质量和步频对结构响应敏感程度的比值与参数波动量以及参数的统计特征有关, 因此计算参数发生不同程度波动时结构的敏感程度比值, 如图11所示.

	Figure Option View Download New Window
	图11 结构响应对行人质量和步频的敏感性比值Fig.11 Ratio between the influence of pedestrian weight and stride frequency

图11表示对应不同行人平均质量以及步频取值的结构响应敏感性系数的分布.从敏感性比值上可以看出, 行人步频波动对结构响应的影响较大, 在步频与质量较小时, 步频对结构响应的影响显著高于质量的影响, 随着步频与质量的增大, 这两个参数对结构响应的影响程度逐渐接近.

5 结论

基于概率理论, 结合人群作用下结构响应的频谱分析法, 探究了典型藏式古建木结构振动对人群荷载参数(行人数量、行人质量、行人步频)的敏感性.采用现场调研, 获得了人群荷载参数的分布形式, 获得了各个参数变化对结构动力响应影响的变化规律, 主要结论归纳如下:

1)通过对典型藏式古建木结构进行概念分析、现场实测与游客行走特征调研, 获得了结构的前三阶模态频率与振型, 并且得到了行人步频的统计分布规律, 服从均值为1.68 Hz的正态分布.

2) 与行人数量和行人质量相比, 行人步频对结构响应的影响最为显著, 行人平均质量的变化对结构响应的影响是行人数量发生同样百分比变化时的1.5~2倍; 而在同样变化幅度下, 行人平均步频的波动对结构响应的影响可达行人数量的5倍.可见, 相比控制步频而言, 控制行人数量对减弱结构动力响应效果相对较弱, 可通过控制步速来有效减轻结构动力响应.

3)在低频行走、质量较小的行人群体中, 结构响应对步频的敏感程度更高, 也就是说, 步频微小的波动会产生较大的结构响应波动.

在工程上, 一般通过控制行人数量来实现人群作用下结构响应的控制.但本研究发现, 结构振动响应对步频更为敏感, 因此可以考虑通过控制行人步频来控制结构的响应.由于行走步频变化较大, 可控范围也相应较广, 因此通过控制行走步频来减轻结构的振动是一种可供借鉴的方法, 本研究为控制人致振动提供了新的依据.

参考文献

文献列表

[1]	BACHMANN H, PRETLOVE A J, RAINER H. Dynamic forces from rhythmical human body motions, practical guidelines[C]//Vibration problems in structures. Basel, 1995. [本文引用:1]
[2]	International Organization for Stand ardization. Bases for design of structures-serviceability of buildings and walkways against vibration: ISO 10137-2007[S]. Switzer Land , 2007. [本文引用:1]
[3]	简方梁, 吴定俊, 李奇. 上海虹桥车站人行走廊人致振动分析[J]. 振动与冲击, 2010, 29(8): 136-140. JIAN Fangliang, WU Dingjun, LI Qi. The human induced vibration analysis of corridor in Shanghai Hongqiao Station[J]. Journal of Vibration and Shock, 2010, 29(8): 136-140. (in Chinese) [本文引用:1]
[4]	高延安, 杨庆山. 行走人群-结构相互作用模型研究[J]. 振动与冲击, 2016, 35(23): 153-159. GAO Yang’an, YANG Qingshan. The analysis of Crowd-Structure interaction model[J]. Journal of Vibration and Shock, 2016, 35(23): 153-159. (in Chinese) [本文引用:1]
[5]	MCKAY M D, BECKMAN R J, CONOVER W J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code[J]. Technometrics, 1979, 21(2): 239-245. [本文引用:1]
[6]	CUKIER R I, FORTUIN C M, SHULER K E. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. I: Theory[J]. The Journal of Chemistry Physics, 1973, 59: 3873. [本文引用:1]
[7]	SALTELLI A, MARIVOET J. Non-parametric statistics in sensitivity analysis for model output: a comparison of selected techniques[J]. Reliability Engineering and System Safety, 1990, 28(2): 229-253. [本文引用:1]
[8]	MORRIS M D. Factorial sampling plans for preliminary computational experiments[J]. Technometrics, 1991, 33(2): 161-174. [本文引用:1]
[9]	SOBOL I M. Sensitivity estimates for nonlinear mathematical models[J]. Math Modeling & Computational Experiment , 1993, 1(4): 407-414. [本文引用:1]
[10]	GARSON G D. Interpreting neural-network connection weights[J]. AI Expert, 1991, 6(4): 47-51. [本文引用:1]
[11]	JULIAN D, OLDEN D A J. Illuminating the “black box”: a rand omization approach for understand ing variable contributions in artificial neural networks[J]. Ecological Modeling, 2002, 154(1/2): 135-150. [本文引用:1]
[12]	MURIEL G, IOANNIS D, SOVAN L. Two-way interaction of input variables in the sensitivity analysis of neural network models[J]. Ecological Modeling, 2006, 195(1/2): 43-50. [本文引用:1]
[13]	蔡毅, 邢岩, 胡丹. 敏感性分析综述[J]. 北京师范大学学报(自然科学版), 2008, 44(1): 9-15. CAI Yi, XING Yan, HU Dan. On sensitivity analysis[J]. Journal of Beijing Normal University(Natural Science), 2008, 44(1): 9-15. (in Chinese) [本文引用:1]
[14]	秦权, 林道锦, 梅刚. 结构可靠度随机有限元理论及工程应用[M]. 北京: 清华大学出版社, 2006: 76-78. QING Quan, LIN Daojin, MEI Gang. Structural reliability stochastic finite element theory and engineering application [M]. Beijing: Tsinghua University Press, 2006: 76-78. (in Chinese) [本文引用:1]
[15]	王春光, 石永久, 王元清, 等. 结构可靠度计算中的敏感性因素分析[J]. 清华大学学报(自然科学版), 2000, 40(6): 108-111. WANG Chunguang, SHI Yongjiu, WANG Yuanqing, et al. Sensitive factor analysis for structural reliability calculations[J]. Journal of Tsinghua University (Science & Technology), 2000, 40(6): 108-111. (in Chinese) [本文引用:1]
[16]	ZIVANOVIC S, PAVIC A, INGÓLFSSON E T. Modeling spatially unrestricted pedestrian traffic on footbridges[J]. Journal of Structural Engineering, 2010, 136(10): 1296-1308. [本文引用:1]
[17]	国家体育总局. 2014年国民体质监测公报[R]. 北京, 2014. General Administration of Sport of China, The national physique monitoring bulletin of 2014[R]. Beijing, 2014. (in Chinese) [本文引用:1]

1995

0.0

... 在人致荷载模拟中,单人荷载通常采用傅里叶级数模型^[1],而在考虑人群效应时,通常采用 N倍的单人荷载^[2]作为作用在结构上的人群荷载,其中N为行人数量 ...

2007

0.0

2010

0.0

简方梁, 吴定俊, 李奇. 上海虹桥车站人行走廊人致振动分析[J]. 振动与冲击, 2010, 29(8): 136-140.

JIAN

Fangliang

, WU

Dingjun

, LI

. The human induced vibration analysis of corridor in Shanghai Hongqiao Station[J]. Journal of Vibration and Shock, 2010, 29(8): 136-140. (in Chinese)

Based on the theories of mode synthesis and mode superposition, human-induced vibration of pedestrian suspension corridor in Shanghai Hongqiao railway station was analyzed using general finite element software combined with self-compiling program. Three different load models were developed to investigate the dynamical effects induced by people in the corridor. Model one is a single person load model given by BS5400, model two is regular crowd loads, and model three considers random crowd loads. The results show that the method given by BS5400 is suitable for estimation of structure response, when the step frequency of walking is far away from the fundamental frequency of the structure. Otherwise the regular crowd loads or the random crowd loads model should be adopted according to the probability of synchronization of crowds. Moreover, it indicates that among all the factors of human force affecting the acceleration response of the corridor, the step frequency is most significant, next comes the dynamic load factor (DLF) and the probability of synchronization of pedestrian , and final is the density of crowd. The comfort evaluation of the pedestrian corridor was conducted using ISO10137’s method, the results show that its vibration serviceability is not so good in"running case" and in “walking case” with step frequency close to the fundamental frequency of the structure.

(1.Department of Bridge Engineering, Tongji University, Shanghai, 200092, China)

采用模态综合与模态叠加理论、应用通用有限元软件与自编程序相结合的方法对上海虹桥站人行走廊的人致振动问题进行分析。考虑BS5400荷载、有序排列人群荷载和随机人群荷载三种荷载模式下的结构响应，指出在步频与结构频率相差较远时，可以采用BS5400荷载模式计算人致振动响应，而当人群荷载频率与结构频率相近时，可根据人群荷载同步调概率的高低选用有序人群荷载模型或随机人群荷载模型。并指出在人行荷载的各个参数中，步频对结构的加速度响应影响最大，其次是动载因子与人群荷载的同步调概率，最后才是人群荷载的集度；最后采用ISO10137标准对人行走廊的振动舒适性进行评价，结果显示接近结构基频的“步行”及“跑动”工况下，其振动舒适性较差。

... 简方梁等^[3]通过有限元模拟,分析了不同人群荷载排列工况下结构响应的特征 ...

2016

0.0

高延安, 杨庆山. 行走人群-结构相互作用模型研究[J]. 振动与冲击, 2016, 35(23): 153-159.

GAO

Yang’an

, YANG

Qingshan

. The analysis of Crowd-Structure interaction model[J]. Journal of Vibration and Shock, 2016, 35(23): 153-159. (in Chinese)

Each pedestrian is simulated as a lump mass and two spring-damper legs and walking crowd-structure interaction (CSI) model is established employing the Lagrange’s equations. First of all, the structural response and dynamic characteristics of crowd-structure system are studied. Second, the crowd number inducing structural response is analyzed. Finally, two different walking styles including queue and side by side inducing different structural response are researched. The simulation analysis shows that the change of structural response and crow-structure system’s dynamic characteristics are increased along with the increment of crowd number. However, the walking style of queue occupying a more uniform distribution crowd density can effectively reduce the response of structure. In order to avoid resonance or exceed fluctuation, the narrow cross section and longitudinal dredge facilities on the deck is recommended to applying the footbridge design.

Beijing’s Key Laboratory of Structural Wind Engineering and Urban Wind Environment, School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China

人群中每个行人简化为一个集中质量和两个弹簧阻尼器腿的模型，利用拉格拉日方程建立了多人行走状态下的人群-结构相互作用模型。首先利用该模型研究了人群引起结构的响应和人群-结构系统的模态特性改变，然后分析了结构响应和系统模态随着人群数量的变化而改变，最后比较了在队列和并排两种不同行走状态下人群结构系统的响应和模态特性的变化。数值分析表明结构的响应和模态特性随着人群数目增加而变化增大，然而行人在结构上分布较为均匀的纵向行走方式能够有效降低结构的响应，为减轻结构的剧烈波动，在人行桥设计时建议采用窄的截面宽度或者在桥面上设置纵向疏导设施以避免人流集中对结构的不利影响。

... 高延安等^[4]采用质量-弹簧模型,对人群中人与人之间的相互作用进行了详细的分析 ...

1979

0.0

... 此外,许多学者已经对参数敏感性分析做过相关研究,其中最常见的模型是多元线性回归模型,而基于拉丁几何取样的多元回归方法、傅里叶敏感性检验法、利用非参数统计方法进行敏感性分析的方法、Morris法、方差分解法等,都是目前常用的敏感性分析方法^[5,6,7,8,9] ...

1973

0.0

1990

0.0

1991

0.0

1993

0.0

1991

0.0

... 目前基于神经网络技术的参数敏感性分析法中主要有Garson法、随机化检验法、PaD2法^[10,11,12] ...

2002

0.0

... 目前基于神经网络技术的参数敏感性分析法中主要有Garson法、随机化检验法、PaD2法^[10,11,12] ...

2006

0.0

... 目前基于神经网络技术的参数敏感性分析法中主要有Garson法、随机化检验法、PaD2法^[10,11,12] ...

2008

0.0

... 应用较为广泛的参数敏感性分析方法是基于概率理论开展的^[13],它具有理论清晰、操作便捷等优点 ...

2006

0.0

... 目前,对于敏感性指标尚无统一的标准,常用的评价准则有基于可靠度一次二阶矩方法的无量纲敏感性指标^[14]、重要性敏感性指标、失效概率对随机变量均值敏感性指标、失效概率对方差敏感性指标^[15]等 ...

2000

0.0

2010

0.0

... 本文作者对藏式古建木结构的构造特征与动力特性进行分析,基于参数敏感性的概率理论,并结合人群作用下结构响应的谱分析法^[16],提出一种结构响应对人群荷载参数敏感性的分析方法 ...

2014

0.0

... 行人体重分布来源于2014年国民体质监测公报^[17] ...