引用本文
吴迪, 吴建建, 刘宝臣. 顶部交通荷载对加筋土挡墙工作性能的影响研究[J]. 北京交通大学学报, 2019,43(3): 57-65.
WU Di, WU Jianjian, LIU Baochen. Research on the influence of top traffic load on the working performance of reinforced retaining wall[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2019,43(3): 57-65.
Doi:10.11860/j.issn.1673-0291.20180173  
Permissions
Copyright©2019, 北京交通大学学报编辑部
北京交通大学学报编辑部 所有
顶部交通荷载对加筋土挡墙工作性能的影响研究
吴迪, 吴建建, 刘宝臣
桂林电子科技大学 建筑与交通工程学院,广西 桂林 541004
通信作者:刘宝臣(1968—),男,内蒙古赤峰人,教授,博士.email:bc0608@163.com.

第一作者:吴迪 (1982—),男,辽宁台安人,讲师,博士.研究方向为岩土工程方面的教学与科研.email:wudi@guet.edu.cn.

收稿日期: 2018-12-07
基金: 广西自然科学基金(2018JJA150076); 桂林电子科技大学研究生教育创新计划资助(2018YJCX91); 桂林电子科技大学研究生优秀学位论文培育项目(17YJPYSS37)
摘要

通过模型试验及相应数值模拟,针对路肩式加筋土挡墙上部交通荷载的作用位置与作用宽度对加筋土挡墙变形稳定性和潜在破裂面的影响进行研究,建立加筋土挡墙受顶部交通荷载作用的计算模型,通过改变计算模型中条形荷载的作用位置D及作用宽度B,探究挡墙变形、筋材应变和稳定性的变化规律.结果表明:当荷载作用中心位置不变时,随荷载作用宽度的增大,墙顶和面板最大变形量均随之减小;筋材最大应变位置由顶层下移至中间层;挡墙安全系数逐渐增大.当荷载作用宽度一定时,在荷载远离面板的过程中,墙顶和面板最大变形量均表现为先增加后减小;各层筋材最大应变位置也远离面板,数值则逐渐减小.挡墙潜在破裂面受荷载作用位置影响显著,破裂面位置整体向荷载方向偏移.

关键词: 交通荷载; 加筋土挡墙; 荷载作用位置; 荷载作用宽度; 工作性能
中图分类号:TU411 文献标志码:A 文章编号:1673-0291(2019)03-0057-09
Research on the influence of top traffic load on the working performance of reinforced retaining wall
WU Di, WU Jianjian, LIU Baochen
School of Architecture and Transportation Engineering, Guilin University of Electronic Technology,Guilin Guangxi 541004, China
Fund:Natural Science Foundation of Guangxi Municipal (2018JJA150076); Innovation Project of GUET Graduate Education(2018YJCX91); GUET Excellent Graduate Thesis Program(17YJPYSS37)
Abstract

Through the model test and the corresponding numerical simulation, the influence of the position and the action width of the top traffic load on the deformation stability and potential failure surface of the shoulder-type reinforced retaining wall is studied. And the calculation model of reinforced retaining wall under the influence of top traffic load is built, by changing the action position D and the action width B of the strip load in the calculation model, the variation law of the deformation of the retaining wall, the strain and stability of the reinforcement are studied. The results show that when the center position of the load remain constant, the maximum deformation of the wall top and the panel decreases with the increase of the load width; the maximum strain position of the reinforcement move from the top layer to the middle layer; the security level of the retaining wall gradually rises. When the load action width is constant, the maximum deformation of the wall top and the panel increases first and then decreases during the proc ess when the load move away from the panel; the maximum strain position of each layer of the reinforcement also move away from the panel, and the value gradually drops. The potential failure surface of the retaining wall is significantly affected by the position of the load, and the overall position of the failure surface shifts toward the load direction.

Keyword: traffic load; reinforced retaining wall; load position; load width; work performance

在山区中高等级公路建设中, 常常面临公路一侧需要开挖而另一侧需要高填方的情况, 为了节约成本, 缩短工期, 路肩式加筋土挡墙是优选方案[1].采用路肩式加筋土挡墙虽然可以较好地稳定路基, 有效收坡, 但墙顶位于路肩处, 路面交通荷载对加筋土挡墙的影响不容忽视[2, 3].然而交通荷载的作用位置、作用范围与行车道的规划有密切联系, 目前不同作用位置和范围的交通荷载对路肩式加筋土挡墙的安全稳定性及筋材应力应变关系的影响, 研究成果还较少.

针对荷载对加筋土挡墙工作特性的影响, 已有一些学者开展了研究.肖成志等[4, 5]和王贺等[6]对返包式加筋土挡墙受墙顶静、动荷载下的受力变形进行了试验研究; 刘明志等[7]和杨果林等[8]通过有限元分析对加筋挡墙中土压力和筋材应力情况进行了研究; 刘泽等[9, 10]进行的现场试验也表明车辆荷载的作用位置对加筋体内的动土压力大小及分布模式有很大影响.国外的学者[11, 12]在进行加筋土挡墙设计时也会充分考虑荷载对加筋挡墙的工作性能影响.

另外, 挡墙的稳定性是加筋土挡墙设计中的重要评价指标.徐超等[13]和朱海龙等[14]都通过模型试验等手段对加筋土挡墙的破坏模式、破裂面位置进行了试验研究; 高江平等[15]的研究表明加筋挡墙上部分的滑动破裂面过均布荷载中心; 叶观宝等[16]和张垭等[17]利用有限元分别就面板类型、面板倾角对加筋挡墙力学特性的影响展开研究; 林宇亮等[18]对柔性网面土工格栅加筋土挡墙的工程特性进行了探讨.国外学者Jozef[19]结合理论分析与数值模拟结果对加筋挡墙内部稳定性进行了研究.

加筋土挡墙的安全稳定性限制了上部荷载在挡墙上分布的范围, 而关于荷载作用位置及作用宽度变化对加筋土挡墙影响的研究目前还较少, 实际工程没有相应理论研究支撑.鉴于此, 本文作者结合室内模型试验, 利用有限元软件对不同作用位置及宽度的条形荷载作用在加筋土挡墙上进行数值分析, 探讨了墙上荷载对挡墙变形稳定性的影响.

1 工程失败案例

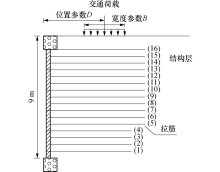
桂林市某高速公路路段路肩式加筋土挡墙全长78 m, 与左侧既有乡道高差约9 m, 填土为粉质黏土, 棕红色, 硬塑.挡墙加筋情况如图1所示, 面板采用149 cm× 49 cm× 20 cm槽型板.交通荷载的中心作用点与面板的距离定义为荷载的位置参数D, 荷载的分布范围定义为作用宽度参数B.受节假日出游和上下班交通流的影响, 该公路上交通荷载的D、B具有一定的指向性.由于设计之初未充分考虑墙顶上部交通荷载的影响, 加之后期外来因素导致公路货车超载频繁, 在公路通车运营5年后, 挡墙面板开始出现变形, 局部地区起鼓严重, 发生推移破坏, 路面出现纵向裂缝并下沉, 现场破坏情况见图2.可见墙顶上交通荷载的形式对路肩式加筋土挡墙的设计、运营具有显著的影响.

图1 加筋土挡墙示意图Fig.1 Diagrams of reinforced retaining wall

图2 现场破坏情况Fig.2 Site damage condition

2 室内模型试验

为了解加筋挡墙失效机理、探究交通荷载分布形式对路肩式加筋土挡墙影响, 进行了模型试验和相应数值模拟.考虑到试验条件限制, 试验模型简化设置3层加筋, 其余参考案例设置.根据模型试验建立并分析有限元模型, 验证试验及数值分析结果.

2.1 试验材料

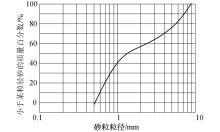
填料为石英砂, 不均匀系数 Cu为3.93, 曲率系数 Cc为0.47, 颗粒级配曲线见图3.试验时采用分层压实控制石英砂的密度约为2.3 g/cm3, 重度为26 kN/m3, 通过室内筋土界面直剪试验得到墙后被挡土体的有效内摩擦角 φ为36° , 黏聚力 с为1.0 kPa.加筋材料选用的是玻璃纤维土工格栅, 其物理力学参数见表1.

图3 石英砂颗粒级配曲线Fig.3 Grain size distribution of the quartz sand

表1 试验用格栅力学参数 Tab.1 Mechanical parameters of geometric
2.2 试验方案

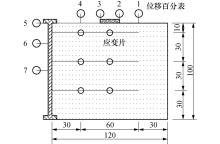
挡墙尺寸及试验监测仪器布置如图4所示.挡墙模型尺寸为120 cm× 60 cm× 100 cm(长× 宽× 高), 筋材分3层布置, 层间距为30 cm, 筋长 L均为90 cm.加载板刚性, 宽度为20 cm, 长度为58 cm, 并在模型箱内壁涂抹凡士林减小边界效应, 保证是平面应变问题.

图4 模型尺寸及监测仪器布置(单位: cm)Fig.4 Size of the model and layout of the measuring instruments (unit: cm)

挡墙填筑完成后静置2~3 d, 使其变形稳定.然后对其顶部逐级加载, 每级加载0.5 t, 历时60 min, 最高加载到3 t.挡墙顶面和侧壁的位移由百分表监测, 按照加载0、1、2、5、10、20、30、60 min时读数, 在整个加载过程中每一级加载重复一次.应变片和土压力盒数据由静态应变仪采集, 1 min采集一次.挡墙侧壁百分表布置见图5.

图5 挡墙侧壁百分表布置Fig.5 Retaining wall sidewall dialgauge layout

3 模型的建立与验证
3.1 有限元模型建立

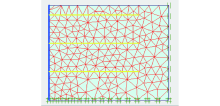
加筋土挡墙为平面应变问题, 可选用15节点平面应变模型; 挡墙填土选用排水的Mohr-Coulomb模型; 面板采用弹性梁单元; 筋材采用仅能拉伸的弹性单元; 筋-土界面摩擦系数选用0.7.边界条件为两侧水平约束, 底部水平竖向双约束, 有限元计算模型三角形网格划分情况见图6.筋材材料为线弹性, 轴向刚度取1.25 MN/m, 填土具体参数如表2, 面板材料参数详见表3.

图6 有限元网格图Fig.6 Finite element meshes

表2 土体材料参数 Tab.2 Material parameters of soil
表3 面板和筋材材料参数 Tab.3 Parameters of facing and reinforcement material
3.2 有限元模型验证

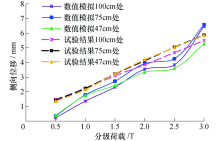
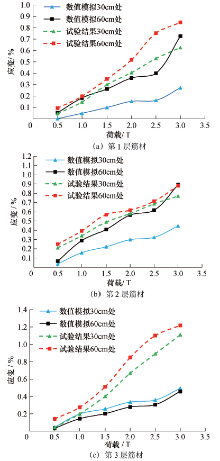
为验证所建有限元模型的可靠性, 将室内模型试验结果与有限元计算值进行对比, 图7和图8分别为挡墙面板位移和各层筋材应变的试验值与计算值对比曲线.从图中可知, 挡墙面板位移和各层筋材应变的有限元计算结果和试验值之间有较好的吻合, 挡墙面板水平位移结果均表现出“ 上部位移大、下部位移小” 的特点, 各层筋材应变随荷载的增大而增大.通过对比可知, 建立的挡墙数值模型能较好地反映加筋挡墙受墙顶条形荷载时的变形、受力规律, 为后续深入研究奠定基础.

图7 挡墙面板水平位移对比曲线Fig.7 Correlation curves of retaining wall panel horizontal displacement

图8 筋材应变对比曲线Fig.8 Correlation curves of tensile strain

4 结果分析

通过改变有限元模型中条形荷载的D、B, 分析加筋挡墙横向与竖向变形及筋材应力分布的变化.此处荷载作用宽度发生变化时, 荷载的大小不变, 随之变化的是挡墙顶部的压强.

4.1 对面板水平位移的影响

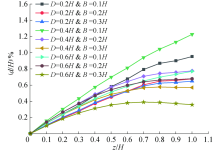
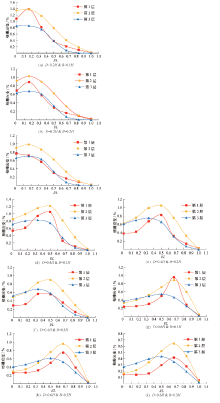
数值模型中挡墙高度为H, 选取面板上不同高度z处的水平位移值d, 得到挡墙受不同位置及宽度的条形荷载作用下面板水平位移沿墙高的分布情况, 如图9所示.从图9可知, 在土压力及条形荷载的共同作用下, 挡墙面板水平位移表现出墙高上部位移大、下部位移小的特点, 这点与文献[5]中的试验结果相印证.以D=0.4H且B=0.1H情况为例, 在墙高为1.0H、0.7H、0.4H、0.1H处, 面板最大水平位移值分别为1.23%、0.94%、0.57%、0.16%倍挡墙高度.

图9 挡墙水平位移沿墙高的分布Fig.9 Distribution of lateral deformations of retaining wall along wall height

当 D不变时, 面板最大水平位移值与 B成负相关, 这与单位条形荷载的大小有关.荷载靠近面板时, 最大水平位移出现的位置随 B的变化不明显, 均出现在面板最上部, 其水平位移值也明显大于其他位置.这与常规情况下的面板水平位移变化规律差异较大, 说明荷载作用位置显著影响了挡墙面板的水平变形.当荷载逐渐远离面板时, 面板最大水平位移出现位置随B的增大而向下移动, 表现出中间大两头小的“ 鼓肚” 形式, 与传统面板水平位移变化规律相同, 如D=0.6H的情况.当B一定时, 面板最大水平位移值随D的增大表现为先增加后减小.如当B=0.1H, D=0.2H、0.4H、0.6H的最大水平位移值依次为0.95%、1.23%、0.77%倍挡墙高度.

4.2 对墙顶竖向沉降的影响

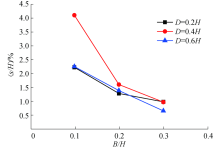
加筋挡墙在受到不同位置及宽度条形荷载时, 最大竖向沉降的发生位置均在荷载施加处, 最大竖向沉降对比曲线如图10所示, 由图可知, 当D不变时, 墙顶处最大沉降值s和挡墙高度的比值与B成负相关; B不变时, 墙顶最大沉降值随荷载合力作用点与面板间距离D的增加先增大后减小.从潜在破裂面的角度分析, D=0.4H时的计算破裂面与理论破裂面较接近, 破坏挡墙稳定性.

图10 最大竖向沉降对比曲线Fig.10 Correlation curves of maximum vertical settlement

4.3 对筋材应变的影响

对各组有限元模型测得的各层筋材应变数据进行统计分析, 结果见图11.模型的筋材布置情况从下至上共3层, 布置高度分别为0.3H、0.6H、0.9H, 每层筋材上等间距选取7个数据提取点, 记提取点与面板的距离为l, 筋长为L, 提取点在筋材上位置则用l/L表示.

图11 筋材应变沿长度方向变化Fig.11 Distribution of geogrids’ strains along length

由图知, 当B保持不变时, 各层筋材最大应变发生位置随D的增大而后移, 即远离面板位置; 最大应变的数值随之减小, 即荷载远离面板, 对挡墙有利, 这与工程经验相一致.特别当D=0.2H且B=0.1H, 即荷载作用离面板近且集中时, 这时顶层筋材应变最大达到了1.38%, 且明显大于底层筋材最大应变0.86%.当荷载作用位置逐渐远离面板, 各层筋材应变差异随之逐渐减小, 但仍保持顶层筋材应变最大.

当D保持不变时, 各层筋材最大应变发生位置随B的增大在水平方向上变化不大, 在竖直方向上由顶层下移至中间层, 且中间层应变与另外两层应变的差异逐渐增大, 表现为荷载逐渐向深部传递; 最大应变的数值随B的增大而减小, 即一定大小的荷载, 作用范围越广, 对挡墙越有利.特别当D=0.6H且B=0.3H, 即荷载作用远离面板且作用范围广时, 这时中间层筋材应变最大, 与其他层筋材应变差异较大, 但自身应变数值并不是很大, 为0.64%.

4.4 对挡墙整体稳定性的影响

利用强度参数折减算法求出各种荷载下挡墙的安全系数, 并进行对比分析, 如图12所示.从图12(a)曲线变化可知, 当荷载的作用位置一定时, 挡墙安全系数与荷载的作用宽度成正相关, 即荷载作用宽度越大, 挡墙稳定性越高, 如D=0.4H时, B=0.3H对应挡墙安全系数约为B=0.1H时的2.22倍; 由图12(b)可得, 当荷载作用宽度为定值时, 挡墙安全系数随荷载远离面板而越来越小.

图12 加筋土挡墙整体稳定性对比曲线Fig.12 Correlation curves of overall stability factor for reinforced retaining wall

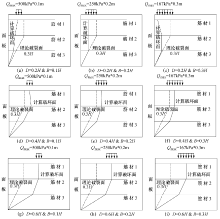
在图13中, 挡墙上部承受不同形式交通荷载Q, 假定各层筋材在最大应变处拉断, 做出各种荷载情况下挡墙的计算破坏面, 虚线表示“ 0.3H” 法理论破裂面, 实线表示计算破裂面位置.由图可知, 计算破坏面对荷载位置敏感, 对荷载作用宽度不敏感; 计算破坏面的形状与“ 0.3H” 法滑裂面和摩尔库伦破裂面形状均有一定差别, 可见荷载的作用位置及宽度对破坏面有显著影响, 表现为计算破坏面的位置整体向荷载合力作用点方向延伸.在荷载远离面板的过程中, 挡墙计算破坏面也随之远离面板, 这一变化造成了挡墙主动区筋材长度增加, 而在筋长总长保持不变的情况下, 锚固区筋长长度逐渐减小, 维持挡墙稳定的有效筋材长度的减小, 对挡墙稳定性造成影响, 即安全系数的降低.因此, 在路肩式加筋挡土墙的设计过程中, 应充分考虑上部荷载的作用位置, 否则将存在安全隐患.

图13 挡墙计算破坏面分布Fig.13 Distributions of failure surface calculation for retaining wall

5 结论

针对路肩式加筋挡墙工作性能受交通荷载影响的问题, 采用模型试验并结合有限元分析, 对路肩式加筋挡墙墙顶受不同位置和不同宽度交通荷载作用下的挡墙变形、筋材应变和稳定性进行研究.考虑对比的有效性, 分析基于总荷载大小不变条件下, 荷载作用位置和作用宽度变化对于路肩式加筋挡墙工作性能的影响.得到以下结论:

1)挡墙顶部沉降值、面板水平位移值均与B成负相关; 随D的增大先增加后减小, 当B=0.1H, D=0.2H、0.4H、0.6H时的最大水平位移值依次为0.95%、1.23%、0.77%倍挡墙高度.当D较小时, 面板最大水平位移的位置随B的变化不明显; D较大时, 面板最大水平位移的位置随B的增大呈下移趋势.

2)各层筋材最大应变发生位置随D的增大而远离面板; 最大应变数值随D的增大而减小.当荷载作用离面板近且集中时, 顶层筋材应变最大且明显大于底层筋材应变.

3)各层筋材最大应变发生位置随B的增大在水平方向上变化不大, 在竖直方向上由顶层下移至中间层, 表现为荷载逐渐向深部传递; 最大应变的数值随B的增大而减小.

4)挡墙在墙顶受条形荷载作用下的潜在破裂面形式受荷载作用位置的影响显著, 表现为潜在破裂面的出现位置整体向荷载作用位置移动.在潜在破裂面远离面板的过程中, 筋材有效锚固长度减小, 导致挡墙安全系数逐渐降低; 而当荷载的作用位置一定时, 挡墙安全系数与荷载的作用宽度成正相关.

参考文献
[1] 杨广庆, 徐超, 张孟喜. 土工合成材料加筋土结构应用技术指南[M]. 北京: 人民交通出版社, 2016.
YANG Guangqing, XU Chao, ZHANG Mengxi. Geosynthetics reinforced soil structure application guidance[M]. Beijing: China Communications Press, 2016. (in Chinese) [本文引用:1]
[2] 王怡, 罗丹霞, 杜雪芳, 等. 车辆荷载下土工格栅加筋挡土墙动力特性研究[J]. 西南科技大学学报, 2014, 29(2): 37-39.
WANG Yi, LUO Danxia, DU Xuefang, et al. Research on dynamic characteristics of geogrid reinforced retaining walls under vehicle load[J]. Journal of Southwest University of Science and Technology, 2014, 29(2): 37-39. (in Chinese) [本文引用:1]
[3] 魏平, 魏静, 肖宏, 等. 列车荷载下桩网路基加筋垫层土工格栅受力影响因素分析[J]. 北京交通大学学报, 2017, 41(3): 77-83.
WEI Ping, WEI Jing, XIAO Hong, et al. Study on stress influential factors of geogrids of geosynthetic reinforcement layer in pile net subgrade structure under train load[J]. Journal of Beijing Jiaotong University, 2017, 41(3) : 77-83. (in Chinese) [本文引用:1]
[4] 肖成志, 陈倩倩, 韩杰, 等. 顶部条形基础作用下加筋挡墙性能的试验研究[J]. 岩土力学, 2013, 34(6): 1586-1592.
XIAO Chengzhi, CHEN Qianqian, HAN Jie, et al. Experimental study of performance of geogrid-reinforced retaining wall subjected to load from strip foundation at top surface of wall[J]. Rock and Soil Mechanics, 2013, 34(6): 1586-1592. (in Chinese) [本文引用:1]
[5] 肖成志, 王嘉勇, 周霞. 受静载和循环荷载作用的基础下加筋挡墙工作性能分析[J]. 岩石力学与工程学报, 2017, 36(6): 1542-1550.
XIAO Chengzhi, WANG Jiayong, ZHOU Xia. Performance of geogrid-reinforced soil retaining walls subjected to static and cyclic footing loadings[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(6): 1542-1550. (in Chinese) [本文引用:2]
[6] 王贺, 杨广庆, 吴连海, 等. 墙顶荷载对加筋土挡墙工作特性影响的试验研究[J]. 岩石力学与工程学报, 2014, 32(12): 2573-2581.
WANG He, YANG Guangqing, WU Lianhai, et al. Experimental study of geogrids reinforced retaining wall under overhead loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 32(12): 2573-2581. (in Chinese) [本文引用:1]
[7] 刘明志, 杨广庆. 列车荷载对路堤式加筋土挡墙结构力学特性影响的数值模拟[J]. 长江科学院院报, 2014, 31(3): 96-100.
LIU Mingzhi, YANG Guangqing. Numerical simulation on the influence of train load on the structural behaviors of reinforced earth retaining wall embankment[J]. Journal of Yangtze River Scientific Research Institute, 2014, 31(3): 96-100. (in Chinese) [本文引用:1]
[8] 杨果林, 申权, 徐健楠. 高速公路绿色加筋格宾挡墙数值分析及现场试验[J]. 中国公路学报, 2015, 28(6): 18-23.
YANG Guolin, SHEN Quan, XU Jiannan. Site test and numerical analysis on reinforced earth retainingwall with green gabion on expressway[J]. China Journal of Highway and Transport, 2015, 28(6): 18-23. (in Chinese) [本文引用:1]
[9] 刘泽, 史克友, 黄天琪, 等. 车辆荷载作用下加筋土挡墙的静动响应现场试验[J]. 水文地质工程地质, 2017, 44(4): 91-97.
LIU Ze, SHI Keyou, HUANG Tianqi, et al. Field test of static and dynamic response of reinforced earth retaining wall under vehicle load[J]. Hydrogeology & Engineering Geology, 2017, 44(4): 91-97. (in Chinese) [本文引用:1]
[10] 刘泽, 蒋梅东, 黄天棋, 等. 车辆荷载在挡土墙上引起的附加土压力研究[J]. 公路交通科技, 2018, 35(7): 22-28.
LIU Ze, JIANG Meidong, HUANG Tianqi, et al. Study on additional earth pressure on retaining wall caused by vehicle load[J]. Journal of Highway and Transportation Research and Development, 2018, 35(7): 22-28. (in Chinese) [本文引用:1]
[11] GAUDIO D, MASINI L, RAMPELLO S. A performance-based approach to design reinforced-earth retaining walls[J]. Geotextiles and Geomembranes, 2018, 46(4): 470-485. [本文引用:1]
[12] YAZDANDOUST M. Investigation on the seismic performance of steel-strip reinforced-soil retaining walls using shaking table test[J]. Soil Dynamics and Earthquake Engineering, 2017, 97: 216-232. [本文引用:1]
[13] 徐超, 梁程, 罗玉珊. 有限填土加筋土挡墙的稳定性及破坏模式分析[J]. 水文地质工程地质, 2017, 44(1): 104-109.
XU Chao, LIANG Cheng, LUO Yushan. Stability and failure modes of geosynthetic reinforced soil wallwith limited retained backfill[J]. Hydrogeology &Engineering Geology, 2017, 44(1): 104-109. (in Chinese) [本文引用:1]
[14] 朱海龙, 刘一通, 邢义川, 等. 加筋土挡墙破坏形式的离心模型试验研究[J]. 长江科学院院报, 2014, 31(3): 58-64.
ZHU Hailong, LIU Yitong, XING Yichuan, et al. Experimental investigation on failure modes of reinforced-sand retaining wall[J]. Journal of Yangtze River Scientific Research Institute, 2014, 31(3): 58-64. (in Chinese) [本文引用:1]
[15] 高江平, 俞茂宏, 胡长顺, 等. 加筋土挡墙滑动破裂面的大型模型试验[J]. 长安大学学报(自然科学版), 2005, 25(6): 6-9.
GAO Jiangping, YU Maohong, HU Changshun, et al. Large model experiment on sliding rupture of reinforced earth retaining wall[J]. Journal of Chang’an University(Natural Science Edition), 2005, 25(6): 6-9. (in Chinese) [本文引用:1]
[16] 叶观宝, 张振, 邢皓枫, 等. 面板对路堤式加筋土挡墙力学特性的影响[J]. 岩土力学, 2012, 33(3): 881-886.
YE Guanbao, ZHANG Zhen, XING Haofeng, et al. Influence of facing on mechanical behavior of reinforcedretaining wall for embankment[J]. Rock and Soil Mechanics, 2012, 33(3): 881-886. (in Chinese) [本文引用:1]
[17] 张垭, 汪磊, 刘华北. 面板倾角对模块式面板加筋土挡墙筋材内力的影响[J]. 岩土工程学报, 2017, 39(9): 1680-1688.
ZHANG Ya, WANG Lei, LIU Huabei. Influence of facing batter angle on reinforcement load of reinforced soilretaining wall with modular block facing[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(9): 1680-1688. (in Chinese) [本文引用:1]
[18] 林宇亮, 杨果林, 许桂林. 柔性网面土工格栅加筋土挡墙工程特性[J]. 中南大学学报(自然科学版), 2013, 44(4): 1532-1538.
LIN Yuliang, YANG Guolin, XU Guilin. Engineering behaviors of geogrid reinforced earth retaining wall of flexible surface[J]. Journal of Central South University (Science and Technology), 2013, 44(4): 1532-1538. (in Chinese) [本文引用:1]
[19] JOZEF V. Internal stability analyses of geosynthetic reinforced retaining walls[J]. Procedia Engineering, 2014, 91: 346-351. [本文引用:1]