岩土材料非线性本构模型的开发与验证

引用本文

张良以, 陈铁林, 张顶立, 安非. 岩土材料非线性本构模型的开发与验证[J]. 北京交通大学学报, 2018,42(6): 9-14.
ZHANG Liangyi, CHEN Tielin, ZHANG Dingli, AN Fei. Development and verification of nonlinear constitutive model for geotechnical materials[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2018,42(6): 9-14.
Doi:10.11860/j.issn.1673-0291.2018.06.002 复制到剪切板

Permissions

岩土材料非线性本构模型的开发与验证

张良以¹, 陈铁林¹, 张顶立¹, 安非²

1.北京交通大学城市地下工程教育部重点实验室,北京 100044

2.北京电力工程有限公司,北京 100070

通讯作者:陈铁林(1970—),男,安徽天长人,教授,博士,博士生导师.email:tlchen1@bjtu.edu.cnn

第一作者:张良以(1990—),男,福建福鼎人,博士生.研究方向为岩土本构数值计算.email:zhangliangyi@bjtu.edu.cn.

收稿日期: 2018-04-19

基金: 国家重点研发计划(2017YFC0805400); 北京市自然科学基金(8161001)

摘要

在增量塑性理论框架下,开发一种适用于岩土材料的非线性数值本构模型,利用开发的模型模拟三轴压缩试验、单轴拉伸试验及三轴拉压组合试验,并与室内试验结果和常用理论模型计算结果进行对比分析.结果表明:本文模型能够更有效地反映岩土体材料压缩、拉伸、压缩到反向拉伸、应变软化及循环加卸载状态,并通过单参数调节实现曲线形式由线性到双曲线的转变,弥补了现有模型的不足.

关键词: 岩土力学; 本构模型; 非线性; 加卸载; 拉压组合; 应变软化

中图分类号:TU45 文献标志码:A 文章编号:1673-0291(2018)06-0009-06

Development and verification of nonlinear constitutive model for geotechnical materials

ZHANG Liangyi¹, CHEN Tielin¹, ZHANG Dingli¹, AN Fei²

1.Key Laboratory for Urban Underground Engineering, Ministry of Education, Beijing Jiaotong University,Beijing 100044, China

2.Beijing Electric Power Engineering Company Limited, Beijing 100070, China

Fund:National Key R&D Plan (2017YFC0805400); Beijing Municipal Natural Science Foundation(8161001)

Abstract

Based on the framework of incremental plasticity theory, a nonlinear numerical model is developed in this paper, which is used to simulate triaxial compression test, uniaxial tensile test and triaxial tensile and compression test, and the numerical results of these laboratory tests are compared with previous experimental results and calculations of existing numerical models. The results show that the model can reflect the conditions of geotechnical materials including stress-strain characteristics, the process from compression to reverse tension, strain softening and cyclic loading-unloading more effectively. It’s able to achieve the transformation from liner stress-strain curve to hyperbolic curve through the adjustment of single parameter, which makes up for the deficiency of the existing constitutive model.

Keyword: soil mechanics; constitutive models; nonlinear; loading and unloading; tension-compression combination; strain softening

文章图片

岩土体作为一种气液固三相混合材料, 其应力应变关系复杂而多变.为了反映岩土体应力应变的非线性特质, Duncan等^[1]提出了经典的双曲线型非线性弹性模型, 得到了广泛的应用.Schanz等^[2]在Duncan-Chang模型的基础上提出一种非线性硬化模型, 以弥补Duncan-Chang模型在反映土体剪胀

性等方面的不足.此外, 相关学者提出抛物线型^[3]、指数型^[4]、幂数型^[5]等非线性弹性模型, 以克服双曲线拟合的不足.上述模型均采用外凸型、单调递增且存在渐近线的单一函数形式, 然而单一固定函数形式难以描述复杂多变的土体本构关系, 因此相继有学者提出更加灵活多变的复合型函数关系^{[6, 7]}.

随着岩土体工程复杂性的增加, 仅仅考虑压缩状态下的应力应变非线性特质往往不够.在复杂的隧道、基坑等工程中, 时常存在卸载、再加载甚至反向拉伸的情况, 单纯以线弹性模型来分析岩土体时常存在较大的差异.故而针对复杂岩土体工程开发出简洁实用的本构模型具有重要的实践意义.

在运用各种非线性弹性模型时, 限制其曲线形式的往往是其渐近线, 为了更好地贴合峰值强度, 而导致整体曲线拟合效果变差.复合型函数虽然能有效适应各种多变的本构关系, 但其复杂性及相关参数的确定难度大大增加, 同时也难以适应峰后各式各样的应变软化曲线.上述不足, 可以通过引入经典的弹塑性理论来克服.

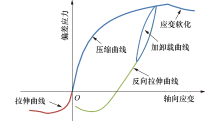
本文作者基于增量塑性理论框架, 引入双参数变切线模量概念, 编程开发一种改进的数值计算模型, 通过与室内试验结果和现有理论模型进行对比, 验证本文模型的正确性与适用性, 以期获得能够反映土体从压缩至拉伸全过程、循环加卸载及应变软化特性的数值计算模型, 非线性应力应变关系示意图如图1所示.

	Figure Option View Download New Window
	图1 非线性应力应变关系示意图Fig.1 Diagram of nonlinear stress-strain relation

1 理论描述

为了便于理解和程序化, 理论以模块化逻辑顺序进行描述, 采用土力学符号约定, 以压为正, 以拉为负, 其中主应力大小依次为σ ₁> σ ₂> σ ₃.

1.1 压缩/拉伸曲线

当前拉伸应力应变形态可归结为3类:应变软化型、应变硬化型和应变强化型^[8].试验结果^{[8, 9, 10]}表明拉伸曲线和常规三轴压缩曲线有着相似的形态, 均具有典型的非线性特性.

当土体处于压缩状态时, 主应力大小均为正值, 主应力最小值σ ₃≥ 0.根据Mohr-Coulomb准则, 屈服函数f_s可表示为

$f_{s} = σ_{1} - σ_{3} N_{φ} - 2 c \sqrt[]{N_{φ}} (1)$

式中:c为黏聚力; φ 为摩擦角; N_φ=(1+sin φ )/(1-sin φ ).

根据式(1)强度准则, 引入应力水平相关变切线模量理念, 可得压缩切线模量计算公式为

$E_{t} = {[1 - R_{c} \frac{(σ_{1} - σ_{3}) (1 - \sin φ)}{2 c \cos φ + 2 σ_{3} \sin φ}]}^{2} E_{i} (2)$

式中:R_c为形状系数, 决定破坏应力下双曲线的形式, 当R_c=0时, 模型将退化为线弹性; E_i为初始模量, 也是最大的切线模量.

当土体处于拉伸状态时, 其主应力最小值σ ₃< 0.引入Rankine准则, 屈服函数f_t表示为

$f_{t} = - σ_{t} - σ_{3} (3)$

式中:σ _t为抗拉强度, 其值为正.

计算中如果直接采用Mohr-Coulomb抗拉强度必然会高估土体的抗拉能力^[11], 秉着简单易用原则, 本文采用抗拉强度截断方式, 仅对抗拉强度进行上限限制

$σ_{t} \leq \frac{c}{\tan φ} (4)$

参照式(2), 可获得拉伸切线模量的表达式

$E_{t} = {(1 + R_{t} \frac{σ_{3}}{σ_{t}})}^{2} E_{it} (5)$

式中:E_it为拉伸初始模量; R_t为拉伸形状系数.为了简化, 当可选参数E_it和R_t空缺的时候, 默认令其与受压状态相同, 即为E_i和R_c.

1.2 加/卸载曲线

相关研究表明^{[10, 12, 13]}, 不论三轴拉伸试验还是单轴拉伸试验, 其卸载再加载曲线与三轴压缩时的形式一致, 均表现为滞回圈形式, 这也说明拉伸情况下的卸载再加载可以与压缩情况下采用相同的形式.因此, 考虑历史应力状态的影响, 由应力水平s区分加/卸载情况.

卸载情况下, 切线模量表达式为

$E_{t} = {[1 - R_{u} (s_{H} - s)]}^{2} E_{u} (6)$

式中:E_u为卸载初始模量; s_H为加载历史最大应力水平; R_u为形状系数, 用于控制加卸载曲线的形式.

在加载情况下, 切线模量的计算方法为

$E_{t} = {[1 - R_{r} (s - s_{L})]}^{2} E_{r} (7)$

式中:s_L为卸载历史最低应力水平, 并设定再加载初始模量E_r与形状系数R_r为可选参数, 默认情况下与卸载情况相同.从式(6)和式(7)可以发现, 当R_u=R_r=0时, 加/卸载切线模量退化为线性, 说明线性假设是本方法的一种特例.

1.3 应力应变关系

将式(2)、式(5)、式(6)和式(7)代入胡克增量定律即可获得应力增量Δ σ _ij与应变增量Δ ε _ij的关系

$Δ σ_{ij} = (K - \frac{2}{3} G) Δ ε_{kk} δ_{ij} + 2 GΔ ε_{ij} (8)$

式中:K为体积模量; 剪切模量G=3KE_t/(9K-E_t); 下标i, j, k=1, 2, 3.

由于切线泊松比的范围限制0< υ _t< 0.5, 故需要对体积模量K进行限制, 0.33E_t≤ K≤ 17E_t.

1.4 塑性修正

根据塑性力学理论, 引入非关联流动法则对达到剪切破坏的应力点进行修正, 并使用关联流动法则修正张拉破坏的应力点.

由Mohr-Coulomb屈服准则, 确定剪切塑性势函数g_s为

$g_{s} = σ_{1} - σ_{3} N_{ψ} (9)$

式中:ψ 为剪胀角; N_ψ=(1+sin ψ )/(1-sin ψ ).

当ψ =φ 时, g_s转变为关联流动法则.对于非关联流动法则, 一般情况下ψ < φ , 通常近似取ψ =0.剪胀角ψ 的引入可以一定程度上反映土体的剪胀性.

由Rankine准则, 张拉塑性势函数g_t为

$g_{t} = - σ_{3} (10)$

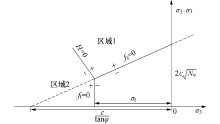
为了便于区分破坏类型, 定义函数H $(σ_{3}, σ_{1})$ =0, 表示f_s=0与f_t=0所围区域的外斜线, 其示意图如图2所示, 表达为

$H = σ_{3} + σ_{t} + A (σ_{1} - B) (11)$

式中:A= $\sqrt[]{1 + {N_{φ}}^{2}}$ +N_φ; B=-σ _tN_φ+2c $\sqrt[]{N_{φ}}$ .

	Figure Option View Download New Window
	图2 破坏分区示意图Fig.2 Diagram of damage division

当弹性试算应力点(σ ₃, σ ₁-σ ₃)位于区域1时, 即f_s> 0且H> 0, 说明发生剪切破坏, 由式(9)确定流动法则, 将应力修正回f_s=0的曲线上.当试算应力点位于区域2时, 即f_t> 0且H< 0, 此时发生张拉破坏, 应由式(10)确定流动法则, 将应力修正回f_t=0的曲线上.

1.5 应变软化

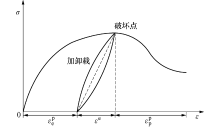
图3为应力应变关系示意图, 可知总应变可表示为ε =ε ^e+ ${ε^{p}}_{e}$ + ${ε^{p}}_{p}$ .其中ε ^e为弹性应变, ${ε^{p}}_{e}$ 与 ${ε^{p}}_{p}$ 之和为塑性应变. ${ε^{p}}_{e}$ 发生于破坏点之前, 可由非线性应力应变关系获得, 而 ${ε^{p}}_{p}$ 发生在破坏点之后, 依据相应流动法则确定.

	Figure Option View Download New Window
	图3 应力应变关系示意图Fig.3 Diagram of stress-strain relation

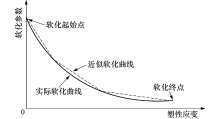
在数学上, 线性函数是最容易处理的, 通过线性插值, 使得计算复杂非线性函数的值更加简单、高效.对于前人提出的各式各样复杂的应变软化曲线^{[10, 14, 15]}, 可将其简化为多段直线的形式进行近似, 塑性应变与软化参数关系示意图如图4所示.

	Figure Option View Download New Window
	图4 塑性应变与软化参数关系示意图Fig.4 Relation of softening parameter and plastic strain

引入损伤变量来描述材料软化的思路^{[14, 15]}, 由于概念明确、使用简单, 并且适用于连续介质数值计算程序的使用.故将黏聚力c $(ε_{p}^{ps})$ 、内摩擦角φ $(ε_{p}^{ps})$ 、剪胀角ψ $(ε_{p}^{ps})$ 、抗拉强度σ _t $(ε_{p}^{pt})$ 定义为相关塑性应变的分段线性函数.其中, $ε_{p}^{ps}$ 表示塑性剪应变, $ε_{p}^{pt}$ 表示塑性拉应变.

以塑性偏应变增量第二不变量J₂'定义塑性剪应变增量Δ $ε_{p}^{ps}$

$Δ ε_{p}^{ps} = \sqrt[]{J_{2}'} = \sqrt[]{\frac{1}{2} Δ e_{ij} Δ e_{ij}} (12)$

式中:Δ e_ij为偏应变增量, i, j=1, 2, 3.

以最大塑性拉应变增量Δ $ε_{3}^{pt}$ 定义塑性拉应变增量Δ $ε_{p}^{pt}$

$Δ ε_{p}^{pt} = |Δ {ε^{p}}_{3}| (13)$

2 模型开发

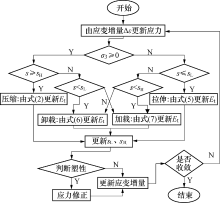
模型基于有限差分算法, 由给定时刻t的应力状态与时步Δ t总应变增量确定时刻t+Δ t的应力状态.基于模块化思路, 采用C++语言编写相应计算程序, 程序计算流程见图5.

	Figure Option View Download New Window
	图5 程序流程图Fig.5 Flow chart of program

3 模型验证

下述模型材料参数依照Duncan-Chang模型参数取法^{[1, 16]}选取, 其中形状系数可按照破坏比R_f取值或进行适当微调以调节曲线形式.而应变软化部分根据1.5节的定义, 依据室内试验结果选取关键节点进行拟合.

3.1 常规三轴压缩试验

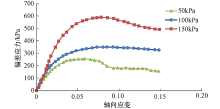
针对某工程土坝含细粒土砂试样进行固结围压为50 kPa、100 kPa、150 kPa的常规三轴固结排水试验, 试验结果^[17]如图6所示.可以发现, 当应力达到峰值后, 有明显的应变软化现象, 此时应当添加应变软化参数, 由于砂土黏聚力为0, 故仅需给出摩擦角φ 随等效塑性剪应变 $ε_{p}^{ps}$ 关系, 当 $ε_{p}^{ps}$ 为0、0.03、0.091、1时, φ 为41.5° 、41.24° 、38.41° 、38.41° .E_i取20.35 MPa, K取12.97 MPa, R_c取0.55, φ 取41.5° , c取0.

根据试验的流程, 数值模拟采用位移加载的方式.首先在选定围压下达到初始应力平衡, 保持围压不变, 固定底部, 顶部施加1.5× 10^-5m/时步的速度, 计算10 000时步, 记录相应的应力与应变.

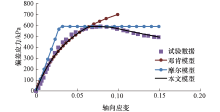
	Figure Option View Download New Window
	图6 常规三轴压缩试验结果图Fig.6 Results of triaxial compression test

为了进一步验证程序计算的正确性和适用性, 将本文模型与Duncan-Chang模型、Mohr-Coulomb模型进行对比.其中, Duncan-Chang模型(邓肯模型)参数取值为:k=147, n=0.8, k_b=117, m=0.23, R_f=0.55, φ =41.5° , c=0.Mohr-Coulomb模型(摩尔模型)选择初始模量E_i=20.35 MPa作为弹性模量, 其余所需参数与上文相同.选取围压150 kPa的试验数据进行对比, 数值计算结果与室内试验结果对比见图7.

	Figure Option View Download New Window
	图7 数值与试验的结果对比Fig.7 Comparison results of simulations and experiment

可以发现, 本文模型与试验数据在应力应变全过程贴合度均很高.而邓肯模型在破坏应力后与试验曲线存在较大误差, 这也说明邓肯模型较适合于荷载小于破坏应力条件下的情况, 而对于具有明显峰值特征的应力应变关系具有一定的局限性.对于峰前非线性应力应变段, 摩尔模型的拟合效果不佳, 存在较大偏差.

3.2 单轴拉伸试验

张丙印等^[13]研发了一种长方体试样的单轴拉伸试验, 由于具有统一的横截面, 其结果与单元测试应力应变状态相似, 非常适合于本构模型的建立以及数值程序的验证.故本文选用直拉试验结果数据来验证数值程序拉伸部分及循环加/卸载部分的正确性.该试验材料选择糯扎渡高塑性黏土, 通过位移控制式加载装置进行加载, 当偏应力达到峰值应力70%时, 通过施加反向位移以实现加/卸载的循环荷载效果.循环荷载下糯扎渡黏土拉应力应变曲线对比见图8.

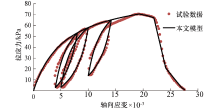	Figure Option View Download New Window
	图8 循环荷载下糯扎渡黏土拉应力应变曲线对比Fig.8 Comparison of tensile stress-stain curves under cycle loading for Nuozadu clay

由于是拉伸试验, 并不发生剪切破坏, 故黏聚力和摩擦角参数设置可以忽略.抗拉强度选择试验结果峰值70.45 kPa, 卸载再加载初始模量取6个卸载再加载初始切线模量的平均值, 单轴拉伸试验数值模型相关参数为E_i=158.82 MPa, K=52.3 MPa, E_u=300.07 MPa, R_t=0.77, R_u=0.82.当 $ε_{p}^{pt}$ 取0、1.5× 10^-4、2.8× 10^-4、6.5× 10^-4、10× 10^-4、11× 10^-4时, σ _t取70.45 kPa、69 kPa、67 kPa、21 kPa、3 kPa、0 kPa.

依照试验流程, 由于是无侧限单轴拉伸试验, 无需施加围压.固定底部, 在顶部施加正向与反向的速度来模拟试验中的加/卸载过程, 循环加/卸载过程详见表1, 其中正为拉, 负为压.

从图8可以发现, 本文模型从起始到软化与试验数据均具有较高的吻合度, 说明本文模型可以用于分析土体拉伸状态的问题.卸载和再加载曲线与试验数据吻合度基本一致, 说明本文提出的近似方法可行, 能够反映出土体循环加/卸载的特性.由于压缩情况与拉伸的一致, 在此不再验证压缩状态下的循环加/卸载的情况.

表1 循环加卸载流程 Tab.1 Step of cyclic loading-unloading

3.3 三轴压缩-拉伸组合试验

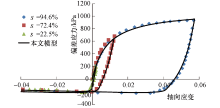
张琰等^[10]应用自制新型卧式三轴仪, 对糯扎渡心墙土料进行三轴压缩-拉伸试验.在室压为150 kPa时, 分别在压缩应力水平s为22.5%、72.4%和94.6%时开始反向加载, 直至试样破坏.

依照试验流程, 采用位移加载方式, 固定底部, 施加围压150 kPa达到初始应力平衡, 然后在顶部施加1.5× 10^-5m/时步的速度, 计算相应步数后, 施加反向速度, 模拟反向加载.三轴压缩-拉伸组合试验数值模型参数详见表2.由于拉伸软化部分并不是本小节的验证内容, 故忽略软化部分.

表2 三轴压缩-拉伸组合试验数值模型参数 Tab.2 Numerical model parameters of triaxial compression-tension test

各组试验结果与数值模拟结果如图9所示.可以发现, 本文模型可以较好地拟合三轴压缩-拉伸组合试验的结果.

	Figure Option View Download New Window
	图9 三轴压缩-拉伸组合试验结果对比Fig.9 Comparison of triaxial compression-tension tests

3.4 形状系数对应力应变曲线的影响

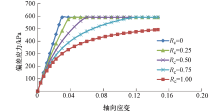
为了分析形状系数对应力应变曲线的影响, 采用单一变量法, 其他所需材料参数见表2, 不考虑应变软化, 形状系数R_c由0至1.0变化.图10给出了不同形状系数情况下的应力应变曲线, 可以发现, 当R_c=0时, 曲线形式与图7中Mohr-Coulomb曲线完全一致, 说明Mohr-Coulomb模型是本文模型的一种特殊形式.随着R_c的增加, 曲线形式从理想弹塑性逐渐向双曲线转变.相比于传统双曲线模型, 塑性理论的引入, 释放了破坏比对于求取峰值渐近线的约束, 使得在相同渐近值的前提下, 应力应变曲线呈现从曲线R_c=0到曲线R_c=1的多样性变化, 更加符合岩土材料性质复杂多样性的特点, 大大增加了数值程序的适用性.

	Figure Option View Download New Window
	图10 不同形状系数情况下应力应变曲线Fig.10 Stress-strain curves under different valus of shape factor

4 结论

基于有限差分算法, 编写开发了一种非线性本构模型.通过常规室内三轴试验、单轴循环拉伸试验及三轴压缩-拉伸组合试验, 验证了所开发模型的正确性与适用性.对比结果表明, 本文模型能够有效地反映土体压缩、拉伸状态下的非线性应力应变特性, 能够反映循环加/卸载状况下及压缩到反向拉伸情况下的非线性特性, 并且通过劣化强度参数有效地反映土体应变软化的特性.

本文模型建立在变切线模量与增量塑性理论基础之上, 材料参数个数少且均能从常规室内试验中获取, 保持了本构模型简单易用的特性.同时, 采用非关联流动法则及增量理论, 在一定程度上可以反映岩土体剪胀性及应力路径的影响.另外, 相较于常用的理论模型, 可通过改变形状系数实现曲线形式由线性到双曲线型的转变, 满足了岩土材料应力应变关系多样性的要求, 具有更广泛的适用性.

参考文献

文献列表

[1]	DUNCAN J M. Nonlinear analysis of stress and strain in soils[J]. Journal of the Soil Mechanics and Foundation Division, 1970, 96(5): 1629-1653. [本文引用:2]
[2]	SCHANZ T, VERMEER P A, BONNIER P G. The hardening soil model: formulation and verification[J]. Beyond 2000 in Computational Geotechnics, 1999: 281-296. [本文引用:1]
[3]	王伟, 卢廷浩, 周干武. 黏土非线性模型的改进切线模量[J]. 岩土工程学报, 2007, 29(3): 458-462. WANG Wei, LU Tinghao, ZHOU Ganwu. Improved tangent modulus of nonlinear soil model[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(3): 458-462. (in Chinese) [本文引用:1]
[4]	GITAU A N, GUMBE L O, BIAMAH E K. Influence of soil water on stress-strain behaviour of a compacting soil in semi-arid Kenya[J]. Soil & Tillage Research, 2006, 89(2): 144-154. [本文引用:1]
[5]	殷德顺, 王保田. 负乘幂本构模型的切线模量[J]. 岩土力学, 2009, 30(7): 2168-2172. YIN Deshun, WANG Baotian. Tangent modulus of negative-power constitutive model[J]. Rock and Soil Mechanics, 2009, 30(7): 2168-2173. (in Chinese) [本文引用:1]
[6]	王丽琴, 鹿忠刚, 邵生俊. 岩土体复合幂-指数非线性模型[J]. 岩石力学与工程学报, 2017, 36(5): 1269-1278. WANG Liqin, LU Zhonggang, SHAO Shengjun. A composite power exponential nonlinear model of rock and soil[J]. Chinese Journal of Geotechnical Engineering, 2017, 36(5): 1269-1278. (in Chinese) [本文引用:1]
[7]	王伟, 宋新江, 凌华, 等. 滨海相软土应力-应变曲线复合指数-双曲线模型[J]. 岩土工程学报, 2010, 32(9): 1455-1459. WANG Wei, SONG Xinjiang, LING Hua, et al. Composite exponential-hyperbolic model for stress-strain curve of seashore soft soil[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(9): 1455-1459. (in Chinese) [本文引用:1]
[8]	张云, 王惠敏, 鄢丽芬. 击实黏土单轴拉伸特性试验研究[J]. 岩土力学, 2013, 34(8): 2151-2157. ZHANG Yun, WANG Huimin, YAN Lifen. Test research on tensile properties of compacted clay[J]. Rock and Soil Mechanics, 2013, 34(8): 2151-2157. (in Chinese) [本文引用:2]
[9]	STIRLING R A, HUGHES P, DAVIE C T, et al. Tensile behaviour of unsaturated compacted clay soils-a direct assessment method[J]. Applied Clay Science, 2015, 112: 123-133. [本文引用:1]
[10]	张琰, 张丙印, 李广信, 等. 压实黏土拉压组合三轴试验和扩展邓肯张模型[J]. 岩土工程学报, 2010, 32(7): 999-1004. ZHANG Yan, ZHANG Bingyin, LI Guangxin, et al. Combined tension-compression triaxial tests and extended Duncan-Chang model of compacted clay[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(7): 999-1004. (in Chinese) [本文引用:4]
[11]	宋焱勋, 李荣建, 刘军定, 等. 结构性黄土的双曲线强度公式及其破坏应力修正[J]. 岩土力学, 2014, 35(6): 1534-1540. SONG Yanxun, LI Rongjian, LIU Junding, et al. A hyperbola strength formula of structural loess and its modifying algorithm under failure stress state[J]. Rock and Soil Mechanics, 2014, 35(6): 1534-1540. (in Chinese) [本文引用:1]
[12]	SUBRAMANIAM P, BANERJEE S. A correction to damping ratio for hyperbolicâhysteretic model for clayey soil[J]. International Journal of Geotechnical Engineering, 2013, 7(2): 124-129. [本文引用:1]
[13]	ZHANG B Y, LI Q M, YUAN H N, et al. Tensile fracture characteristics of compacted soils under uniaxial tension[J]. Journal of Materials in Civil Engineering, 2014, 27(10): 1-11. [本文引用:2]
[14]	沈珠江. 结构性粘土的弹塑性损伤模型[J]. 岩土工程学报, 1993, 15(3): 21-28. SHEN Zhujiang. Elasto-plastic damage constitutive model for structured clay[J]. Chinese Journal of Geotechnical Engineering, 1993, 15(3): 21-28. (in Chinese) [本文引用:2]
[15]	沈珠江. 结构性粘土的非线性损伤力学模型[J]. 水利水运工程学报, 1993(3): 247-255. SHEN Zhujiang. A nonlinear damage model for structured clay[J]. Hydro-Science and Engineering, 1993(3): 247-255. (in Chinese) [本文引用:2]
[16]	冯卫星, 常绍东, 胡万毅. 北京细砂土邓肯-张模型参数试验研究[J]. 岩石力学与工程学报, 1999, 18(3): 327-330. FENG Weixing, CHANG Shaodong, HU Wanyi. Experimental study on parameters of Duncan-Chang model for Beijing fine sand y soil[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(3): 327-330. (in Chinese) [本文引用:1]
[17]	唐洪祥, 张丽娟. 平面应变试验与常规三轴试验条件下含细粒土砂力学特性比较研究[J]. 水利与建筑工程学报, 2015, 13(5): 223-227. TANG Hongxiang, ZHANG Lijuan. Comparative studies on mechanical characteristics of fine-grained sand with plane strain test and triaxial test[J]. Journal of Water Resources and Architectural Engineering, 2015, 13(5): 223-227. (in Chinese) [本文引用:1]

1970

0.0

... 为了反映岩土体应力应变的非线性特质,Duncan等^[1]提出了经典的双曲线型非线性弹性模型,得到了广泛的应用 ...

... 3 模型验证下述模型材料参数依照Duncan-Chang模型参数取法^[1,16]选取,其中形状系数可按照破坏比R_f取值或进行适当微调以调节曲线形式 ...

1999

0.0

... Schanz等^[2]在Duncan-Chang模型的基础上提出一种非线性硬化模型,以弥补Duncan-Chang模型在反映土体剪胀 ...

2007

0.0

王伟, 卢廷浩, 周干武. 黏土非线性模型的改进切线模量[J]. 岩土工程学报, 2007, 29(3): 458-462.

WANG

Wei

, LU

Tinghao

, ZHOU

Ganwu

. Improved tangent modulus of nonlinear soil model[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(3): 458-462. (in Chinese)

Tangent modulus was essential to nonlinear soil model,and it was necessary to understand it properly during numerical simulation.First,a new concept namely half strength index was introduced to build the mathematic properties equations of stress-strain relationship,then the deficiency of hyperbolic expression of the relationship was indicated in terms of it.Second,according to laboratory test data,differential control equation of soil stress-strain relationship was presented and a new 3-parameter stress-strain expression was established.It was shown that the hyperbolic expression was the simplified type of the 3-parameter expression.Third,an improved tangent modulus of soil was obtained based on the new stress-strain expression,and methods to determine its parameters were discussed.Finally,simulation of triaxial test data using the improved tangent modulus was conducted.

1.Department of Civil Engineering Shaoxing College of Art and Science Shaoxing 312000 China 2.Research Institute of Geotechnical Engineering Hohai University Nanjing 210098 China 3.Department of Geotechnical Engineering Nanjing Hydraulic Research Institute Nanjing 210024 China

切线模量描述是土体非线性模型中的一个基本问题。首先,引入“半值强度指数”概念建立了土体应力应变曲线的数学特征方程,分析了双曲线应力应变模型的数学缺陷。接着,根据试验数据分析提出了土体应力应变曲线的控制微分方程,建立了土体应力应变曲线的3参数新模型,新模型克服了双曲线模型的缺陷;证明了双曲线模型是该新模型的特例。最后,在3参数新模型的基础上,改进了土体的切线模量表达,给出了参数确定方法,并对三轴试验结果进行了模拟。

... 此外,相关学者提出抛物线型^[3]、指数型^[4]、幂数型^[5]等非线性弹性模型,以克服双曲线拟合的不足 ...

2006

0.0

... 此外,相关学者提出抛物线型^[3]、指数型^[4]、幂数型^[5]等非线性弹性模型,以克服双曲线拟合的不足 ...

2009

0.0

... 此外,相关学者提出抛物线型^[3]、指数型^[4]、幂数型^[5]等非线性弹性模型,以克服双曲线拟合的不足 ...

2017

0.0

... 上述模型均采用外凸型、单调递增且存在渐近线的单一函数形式,然而单一固定函数形式难以描述复杂多变的土体本构关系,因此相继有学者提出更加灵活多变的复合型函数关系^[6,7] ...

2010

0.0

2013

0.0

... 1 压缩/拉伸曲线当前拉伸应力应变形态可归结为3类:应变软化型、应变硬化型和应变强化型^[8] ...

... 试验结果^[8,9,10]表明拉伸曲线和常规三轴压缩曲线有着相似的形态,均具有典型的非线性特性 ...

2015

0.0

... 试验结果^[8,9,10]表明拉伸曲线和常规三轴压缩曲线有着相似的形态,均具有典型的非线性特性 ...

2010

0.0

... 试验结果^[8,9,10]表明拉伸曲线和常规三轴压缩曲线有着相似的形态,均具有典型的非线性特性 ...

... 2 加/卸载曲线相关研究表明^{[10, 12,13]},不论三轴拉伸试验还是单轴拉伸试验,其卸载再加载曲线与三轴压缩时的形式一致,均表现为滞回圈形式,这也说明拉伸情况下的卸载再加载可以与压缩情况下采用相同的形式 ...

... 对于前人提出的各式各样复杂的应变软化曲线^{[10, 14,15]},可将其简化为多段直线的形式进行近似,塑性应变与软化参数关系示意图如图4所示 ...

... 3 三轴压缩-拉伸组合试验张琰等^[10]应用自制新型卧式三轴仪,对糯扎渡心墙土料进行三轴压缩-拉伸试验 ...

2014

0.0

... 计算中如果直接采用Mohr-Coulomb抗拉强度必然会高估土体的抗拉能力^[11],秉着简单易用原则,本文采用抗拉强度截断方式,仅对抗拉强度进行上限限制 ...

2013

0.0

2014

0.0

... 2 单轴拉伸试验张丙印等^[13]研发了一种长方体试样的单轴拉伸试验,由于具有统一的横截面,其结果与单元测试应力应变状态相似,非常适合于本构模型的建立以及数值程序的验证 ...

1993

0.0

沈珠江. 结构性粘土的弹塑性损伤模型[J]. 岩土工程学报, 1993, 15(3): 21-28.

SHEN

Zhujiang

. Elasto-plastic damage constitutive model for structured clay[J]. Chinese Journal of Geotechnical Engineering, 1993, 15(3): 21-28. (in Chinese)

A constitutive model based on the concepts of damage mechanics has been developed for cemented clays. This model can simulate the process of progressive failure of clays due to the breakage of inter-particle bonding. Accordingly, an elasto-plastic damage matrix has been deduced and a finite element program CONDAM has been compiled based on Biot’s consolidation theory. This model contains 9 parameters which can be easily determined by conventional both confined and unconfined compression test. As an illustration, the test results of Zhanjiang clay and the computed responses of a 10m thick clay foundation under strip surface loading are presented.

Nanjing Hydraulic Research Institute

本文从损伤力学观点出发,建议了一个可以考虑粘土结构破损过程的损伤力学模型,推导了弹塑性损伤矩阵,并制定了相应的计算方法和编制了比奥固结理论的有限元计算程序。模型的计算参数共有9个,可以方便地通过原状土的有侧限和无侧限压缩试验测定。文中从湛江粘土的试验资料出发整理了计算参数,并就10m厚粘土地基上承受均布条形荷载的算例进行了计算,结果定性地与国内外原观资料一致。

... 对于前人提出的各式各样复杂的应变软化曲线^{[10, 14,15]},可将其简化为多段直线的形式进行近似,塑性应变与软化参数关系示意图如图4所示 ...

... 引入损伤变量来描述材料软化的思路^[14,15],由于概念明确、使用简单,并且适用于连续介质数值计算程序的使用 ...

0.0

... 对于前人提出的各式各样复杂的应变软化曲线^{[10, 14,15]},可将其简化为多段直线的形式进行近似,塑性应变与软化参数关系示意图如图4所示 ...

... 引入损伤变量来描述材料软化的思路^[14,15],由于概念明确、使用简单,并且适用于连续介质数值计算程序的使用 ...

1999

0.0

冯卫星, 常绍东, 胡万毅. 北京细砂土邓肯-张模型参数试验研究[J]. 岩石力学与工程学报, 1999, 18(3): 327-330.

FENG

Weixing

, CHANG

Shaodong

, HU

Wanyi

. Experimental study on parameters of Duncan-Chang model for Beijing fine sand y soil[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(3): 327-330. (in Chinese)

... 3 模型验证下述模型材料参数依照Duncan-Chang模型参数取法^[1,16]选取,其中形状系数可按照破坏比R_f取值或进行适当微调以调节曲线形式 ...

2015

0.0

... 1 常规三轴压缩试验针对某工程土坝含细粒土砂试样进行固结围压为50 kPa、100 kPa、150 kPa的常规三轴固结排水试验,试验结果^[17]如图6所示 ...