室内大规模天线系统无线信道空间相关性分析

引用本文

李金兴, 赵友平. 室内大规模天线系统无线信道空间相关性分析[J]. 北京交通大学学报, 2018,42(5): 10-19.
LI Jinxing, ZHAO Youping. Channel spatial correlation analysis for indoor large-scale antenna systems[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2018,42(5): 10-19.
Doi:10.11860/j.issn.1673-0291.2018.05.002 复制到剪切板

Permissions

北京交通大学学报编辑部所有

室内大规模天线系统无线信道空间相关性分析

李金兴, 赵友平

北京交通大学电子信息工程学院,北京 100044

第一作者:李金兴(1988—),男,山东泰安人,博士.研究方向为无线信道测量与建模.email:jinxingli@bjtu.edu.cn.

收稿日期: 2017-05-12

基金: 国家自然科学基金重点项目(61132003); 国家“863”计划项目(2014AA01A706); 教育部重点实验室开放基金(CRKL150203); 北京市自然科学基金(4172046)

摘要

无线信道空间相关性直接影响大规模天线系统的实际性能.基于大型报告厅内的无线信道测量数据,分析了基站天线阵列中不同阵元之间及不同用户之间的无线信道空间相关性.首先对阵元相关系数随阵元间隔的变化进行拟合建模分析,然后研究多用户信道相关性的影响因素.提出了一种负指数衰减余弦模型对其拟合建模.研究结果表明:在水平面内,阵元相关系数随阵元间隔增加近似为负指数衰减波动较小;在垂直面内,阵元相关系数随阵元间隔增加而呈现振荡衰减,基站天线数量增加对多用户信道相关性有明显改善,基站天线数量超过30以后,改善幅度变小但是仍有较明显提升.此外,不同用户之间的大尺度衰落会降低多用户信道正交性,且水平面内用户间大尺度衰落比垂直面内严重. 但是基站阵列中不同阵元间的大尺度衰落对多用户信道正交性的影响十分微弱.

关键词: 无线信道测量; 大规模天线系统; 阵元相关性; 用户相关性

中图分类号:TN929.5 文献标志码:A 文章编号:1673-0291(2018)05-0010-10

Channel spatial correlation analysis for indoor large-scale antenna systems

LI Jinxing, ZHAO Youping

School of Electronic and Information Engineering, Beijing Jiaotong University, Beijing 100044,China

Fund:National Natural Science Foundation of China(61132003); National High-Tech R&D Program of China (863 Program)(2014AA01A706); Ministry of Education Key Laboratory Open Fund(CRKL150203); Beijing Municipal Natural Science Foundation(4172046)

Abstract

The performance of large-scale antenna systems is affected by channel spatial correlation. Based on field channel measurement in an auditorium, this paper analyzes the channel correlation between different antenna elements in the array as well as different users. Antenna correlation coefficients with the antenna spacing are fitted with different models, and the factors that have impact on user channel correlation are also investigated.The results show that the antenna correlation coefficients in the array decays exponentially with antenna spacing in the horizontal plane. However, the antenna correlation tends to be a damped cosine wave in the vertical plane. In this paper, a model of negative exponential attenuation cosine is proposed to fit its modeling.Increasing the number of antenna introduces significant decrease in user channel correlation, especially when the number of antennais less than 30. The large-scale fading between different users degrades the channel orthogonality, and the fading is more severe in horizontal plane. Besides, the impact of large-scale fading over the array on user orthogonality is limited.

Keyword: channel measurement; large-scale antenna systems; antenna correlation; user correlation

文章图片

大规模天线系统(Massive, MIMO或Large-Scale Antenna Systems)是第5代移动通信系统的关键技术之一^[1].它在基站侧使用数十甚至上百根天线在相同频段上同时为多个用户服务, 具有高频谱效率和高能量效率等突出优势.在理想传输条件下, 当基站阵列中的阵元天线远大于用户数量时, 不同用户子信道之间趋于正交, 可以最大限度地提高系统容量^{[2, 3]}.然而, 实际无线传播场景与理想传输条件存在差距, 大规模天线阵列中不同阵元之间及距离较近的用户之间均存在一定的空间相关性, 而且实际系统中基站天线数量也不能无限制增大, 这些都会制约大规模天线系统的性能.

为研究大规模天线系统在实际无线场景中的信道特性和系统性能, 目前针对大规模天线系统的无线信道实地测量已经较为广泛展开.测量场景涵盖城区室外、室内到室外及体育场等多种环境^{[4, 5]}, 测量频段也覆盖了0~6 GHz的低频段和6 GHz以上的高频段(如毫米波频段)^[6].在室外场景的测量中.文献[7]发现紧致型天线阵列(如圆柱阵)由于阵元间隔较小, 导致阵元相关性较高, 信道容量降低.另外, 针对不同阵元相关性的理论模型.文献[8]比较了均匀面阵和均匀线阵的信道容量, 发现阵元相关模型的衰减速度与单调性对信道容量影响显著.

大规模天线系统的高速率优势尤其适合大型室内场馆如报告厅、商场和体育馆等拥有密集用户分布的场景.为此, 本文作者基于大型报告厅场景的实测数据, 详细分析不同空间维度和不同用户分布条件下的基站阵列阵元相关性, 对其进行拟合建模.同时, 针对多用户场景, 重点分析多用户信道的正交性, 并且针对大规模天线阵列的特点, 研究多用户之间的大尺度衰落及阵列尺寸上的大尺度衰落对用户信道正交性的影响.

1 无线信道空间相关性

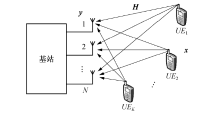
在多用户MIMO(MU-MIMO)系统上行链路中(图1), 假设基站采用大规模天线阵列, 阵元数量为N; 用户端均为单天线, 数量为K; 发送信号为频域多载波信号, 子载波数量为L.在每个子载波上通过信道测量获得相应的信道复增益, 记为H_n_,_k_,_l. 对应于用户k, 它到基站阵列的信道增益向量为H_k_,_l∈ C^N^{× 1}.在所有L个子载波上, 第k个用户到基站阵列中第n个阵元的信道增益向量为H_n_,_k∈ C^L^{× 1}, 对应的信道时域冲击响应可通过离散傅里叶逆变换(Inverse Discrete Fourier Transform, IDFT)得到:h_n_,_k=IDFT{H_n_,_k}.在第l个子载波上, K个用户对基站阵列N个天线阵元的信道传输矩阵为H_l=[H_1,_l, H_2,_l, …, H_K_,_l]∈ C^N^×^K.下面基于以上信道参数给出不同的信道空间相关性表征方法.图1中UE表示用户终端设备, x与y分别表示用户发射信号矢量与基站接收信号矢量, H是信道矩阵.

	Figure Option View Download New Window
	图1 MU-MIMO上行链路Fig.1 Uplink in MU-MIMO

1.1 信道相关系数

针对第k个用户对基站阵列中不同阵元在多个子载波上的信道增益向量, 定义基站阵列中各个阵元之间的信道包络相关系数为^[9]

$\begin{array}{l} {\overset{︿}{ρ}}_{(m, n), k}^{e} = \\ \frac{\sum_{l} (|H_{m, k, l}| - |{\overset{̅}{H}}_{m, k}|) (|H_{n, k, l}| - |{\overset{̅}{H}}_{n, k}|)}{\sqrt[]{\sum_{l} {||H_{m, k, l}| - |{\overset{̅}{H}}_{m, k}||}^{2} \sum_{l} {||H_{n, k, l}| - |{\overset{̅}{H}}_{n, k}||}^{2}}} (1) \end{array}$

式中, $\overset{̅}{H}$ 表示对向量H取平均值.与之对应, 可以定义信道功率相关系数为

$\begin{array}{l} {\overset{︿}{ρ}}_{(m, n), k}^{p} = \\ \frac{\sum_{l} ({|H_{m, k, l}|}^{2} - {|{\overset{̅}{H}}_{m, k}|}^{2}) ({|H_{n, k, l}|}^{2} - {|{\overset{̅}{H}}_{n, k}|}^{2})}{\sqrt[]{\sum_{l} {|{|H_{m, k, l}|}^{2} - {|{\overset{̅}{H}}_{m, k}|}^{2}|}^{2} \sum_{l} {|{|H_{n, k, l}|}^{2} - {|{\overset{̅}{H}}_{n, k}|}^{2}|}^{2}}} (2) \end{array}$

根据文献[10]中的理论分析, 假设阵列中两个阵元上的接收信号包络服从瑞利分布, 它由一个联合高斯分布过程产生, 则信道包络相关系数和功率相关系数均可由此联合高斯分布的协方差导出, 并且最终可证明二者近似相等. 文献[9]利用室外场景的MIMO测量数据, 在视通(Line of Sight, LOS)和非视通(None Line of Sight, NLOS)两种条件下对文献[10]中的结论进行了验证, 结果表明两者确实近似相等.

为了分析实测结果中包络相关系数和功率相关系数的近似程度, 下面定义一个参数来统计两者之间的偏差为

$r^{e, p} = (\sum_{i} | {\overset{︿}{ρ}}_{i}^{e} - {\overset{︿}{ρ}}_{i}^{p} |) / (\sum_{i} |{\overset{︿}{ρ}}_{i}^{e}|) (3)$

式中, 统计量中分子为包络相关系数和功率相关系数的偏差绝对值之和, 分母为包络相关系数绝对值之和. 由于相关系数绝对值可能接近零, 采用求和的方式可以避免异常数据.

此外, 根据每个子载波上某个用户对阵列中所有阵元的信道增益向量, 定义不同用户信道之间的相关系数为

$\begin{array}{l} {\overset{︿}{ρ}}_{k_{1}, k_{2}}^{e} = \\ \frac{\sum_{n} (|H_{n, k_{1}, l}| - |{\overset{̅}{H}}_{k_{1}, l}|) (|H_{n, k_{2}, l}| - |{\overset{̅}{H}}_{k_{2}, l}|)}{\sqrt[]{\sum_{n} {||H_{n, k_{1}, l}| - |{\overset{̅}{H}}_{k_{1}, l}||}^{2} \sum_{n} {||H_{n, k_{2}, l}| - |{\overset{̅}{H}}_{k_{2}, l}||}^{2}}} (4) \end{array}$

各个子载波上的计算结果可以取平均值, 来反映两个用户之间的平均信道相关水平.

1.2 多用户信道正交性

多用户信道发射端协方差矩阵定义为

$R_{tx} = H_{l}^{H} H_{l} (5)$

它体现不同用户信道之间的相关性, 如果不同用户之间的信道正交, 则协方差矩阵的各个特征值均趋于相同.令其特征值向量为λ =[λ ₁, λ ₂, …, λ _s]^T, 且λ ₁≥ λ ₂…≥ λ _s> 0, 则可定义条件数为^[11]

$Con d_{N, K} = λ_{1} / λ_{s} (6)$

条件数为1时, 各个用户信道正交; 条件数为无穷大时, 多用户信道几乎退化为单用户信道.为便于分析, 一般可取条件数的倒数, 其范围为(0, 1), 数值越小, 表明多用户信道的正交性越差.

根据矩阵理论, 矩阵的迹等于特征值之和, 也等于主对角线元素之和, 即

$Tr (H_{l}^{H} H_{l}) = \overset{K}{\sum_{k = 1}} λ_{k} = \overset{N}{\sum_{n = 1}} \overset{K}{\sum_{k = 1}} {|H_{n, k}|}^{2} (7)$

在大规模天线系统中, 基站天线数量远大于用户数量, 即N≫K, 而非零特征值的数量满足S≤ K, 因此MU-MIMO系统实际是把全部信道能量分配到了S个有效的用户子信道上. 每个用户子信道实际上是信道矩阵中多个元素的能量之和, 而信道矩阵条件数就是衡量不同空间用户子信道的相对质量. 因此它对信道小尺度衰落的敏感程度要弱于前面介绍的信道相关系数.

在分析多用户信道正交性或者多用户信道容量时, 需要对MU-MIMO信道矩阵进行归一化(normalization), 使得信道矩阵中各元素的平均功率为单位1, 以便不同条件下的计算结果具有可比性.考虑到大规模天线阵列的特点, 根据不同的研究重点, 可以有不同的归一化方法.对多载波多用户信道测量结果, 分3种信道归一化方法.

1)norm1是不考虑阵列上不同天线之间的接收信号功率变化, 它对任意第k个用户到第n个基站天线的信道增益归一化, 使其满足

$\overset{L}{\sum_{l = 1}} {|H_{n, k, l}^{norm 1}|}^{2} = L (8)$

则归一化过程为

$H_{n, k, l}^{norm 1} = \sqrt[]{\frac{L}{\overset{L}{\sum_{l = 1}} | H_{n, k, l} |^{2}}} H_{n, k, l}^{mea} (9)$

2)norm2是保留某个用户对基站阵列中不同天线阵元上的功率变化, 但是消除不同用户之间的大尺度衰落, 具体过程为^[7]

$H_{k, l}^{norm 2} = \sqrt[]{\frac{N \cdot L}{\overset{L}{\sum_{l = 1}} ‖ H_{k, l}^{mea} ‖^{2}}} H_{k, l}^{mea} (10)$

式中, ||· ||表示向量的2范数.

3)norm3是不仅保留基站阵列上接收信号的功率变化, 而且保留不同用户之间的大尺度衰落, 具体过程为

$H_{l}^{norm 3} = \sqrt[]{\frac{K \cdot N \cdot L}{\overset{L}{\sum_{l = 1}} ‖ H_{l}^{mca} ‖_{F}^{2}}} H_{l}^{mea} (11)$

式中, ||· ||_F表示矩阵的2范数.

2 测量场景与设备

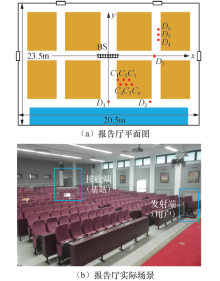
室内大规模天线系统无线信道实际测量中, 接收天线阵列位于报告厅中央, 发射机为单天线, 按位置分为两组, 一组在相邻两排座位集中分布(C₁~C₆), 另一组分散在室内(D₁~D₆), 各有6个位置, 如图2(a)所示.报告厅地面与天花板之间最大高度为5 m, 地面有两级斜坡, 斜率近似相同, 总高度为0.82 m.报告厅内分布着成排的桌椅, 共420座, 如图2(b)所示.每排座椅之间距离为1.2 m, 每排之内相邻两个座位间距为0.53 m.主席台(图2(a)底部)高度0.8 m, 宽度为5.1 m.

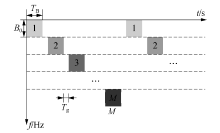
	Figure Option View Download New Window
	图2 室内大规模天线信道测量场景Fig.2 Indoor large-scale antenna channel measurement scenario

大规模天线无线信道测量系统采用多载波宽带测量信号.在一个测量周期内连续探测10个相邻子频段, 每个子频段带宽为20 MHz, 包含64个子载波, 因此总测量带宽为200 MHz.探测信号的时频分布如图3所示.每个子频段带宽为B₀, 占用时长为T_B, T_g为子频段切换的保护时间, 因此总测量带宽为MB₀, 一个测量周期为M(T_B+T_g).关于测量系统的详细原理参见文献[12].

	Figure Option View Download New Window
	图3 探测信号时频分布示意图Fig.3 Sounding signal in time and frequency domains

测量中具体参数配置在表1中.由于5 GHz频段发射功率较低, 在接收端额外增加了一个低噪声放大器, 增益为29 dB.

表1 大规模天线信道测量系统配置参数 Tab.1 Parameter configurations for large-scale antenna channel measurement system

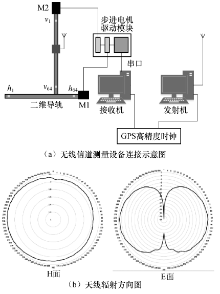
信道测量系统采用大规模虚拟天线阵列, 各模块连接如图4(a)所示.发射机与接收机使用同轴电缆连接外部高精度GPS时钟源, 实现收发时钟同步, GPS时钟源天线置于房顶开阔处以便接收卫星信号.接收机连接虚拟二维天线阵列, 天线阵列由两条步进电机控制的导轨组成. 接收机通过串口控制步进电机运动, 从而实现接收天线位置移动.水平维度内测量64点(h₁-h₆₄), 此时天线在垂直维度的最高点v₁处; 水平维度测量完成后(到达h₆₄), 天线从v₁向下移动到v₃₂, 测量垂直维度内32个天线位置.基站天线高度最高为2.6 m, 用户天线高度为1.2 m.天线辐射方向图如图4(b)所示.

	Figure Option View Download New Window
	图4 基于虚拟大规模天线阵列的信道探测系统Fig.4 Channel sounder system based virtual large-scale antenna array

3 阵元天线信道相关性

3.1 包络相关系数与功率相关系数

基站天线阵列中不同阵元之间的信道包络和功率相关系数可根据式(1)与式(2)计算, 直接得到阵列中某个天线与其他天线的信道相关性.用户C₁和D₁位置在水平面与垂直面的信道包络相关系数显示在图5中. 由于相关系数计算公式中两个向量的先后顺序不影响计算结果, 因此图5中的阵元信道相关系数沿对角线左右对称, 对角线元素为每个阵元的信道自相关, 数值为1.

1)从图5中可以看到, 水平面内的阵元信道相关系数变化随机性很大, 无明显周期性, 但是垂直面内阵元信道相关系数呈现出比较明显的周期变化.在垂直面内, C₁位置的阵元相关系数周期性十分明显, 各个阵元与其他阵元的相关系数随阵元间隔的变化非常一致, 而D₁位置处各阵元间信道相关系数的变化一致性不如C₁位置显著.

2)为了比较信道包络和功率相关系数的差异, 对每个用户位置对应的阵元相关系数取平均值, 以便直接比较. 考虑到数据量和参考区间长度的影响, 水平面和垂直面内分别只分析最大天线间隔为32d₀和16d₀的阵元相关系数, C₁和D₁位置的结果如图6所示.

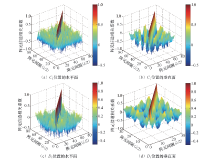	Figure Option View Download New Window
	图5 不同用户位置与空间维度内阵元信道相关系数Fig.5 Antenna correlation for different user locations and spatial dimensions

	Figure Option View Download New Window
	图6 阵元天线信道包络和功率相关系数对比Fig.6 Comparison between the antenna channel envelope and power-correlation

从图6中可以看到, 阵元包络和功率相关系数均非常接近, 这与第1节介绍的已有理论分析和实测结果均吻合.

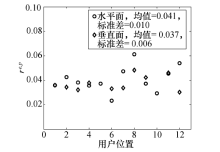
根据式(3), 可以统计各个用户位置对应的信道包络和功率相关系数偏差, 如图7所示. 两种信道相关系数的偏差r^e^,^p在水平面和垂直面内无明显区别, 均值约为0.04, 标准差约为0.01. 这进一步说明二者在数值上近似相等.

	Figure Option View Download New Window
	图7 不同用户位置下阵元天线信道包络和功率相关系数对比Fig.7 Comparison between channel envelope and power correlation under different user position

3.2 射线跟踪仿真

从图5与图6的实测结果可以看到, 水平面和垂直面内阵元信道相关系数随阵元间隔的变化规律显著不同. 为了进一步分析造成此现象的原因, 采用射线跟踪的方法分析空间中多径分量在不同维度的分布情况.仿真中采用发射射线法, 利用相距一定间隔的若干条射线对空间进行扫描, 当射线到达接收点时, 利用接收球判断射线能否被接收端接收.仿真的具体过程可参见文献[13]. 仿真场景按照图2中的实际场景设置, 只是未考虑桌椅等尺寸较小的反射体.表2中列出了仿真系统中的关键参数.仿真中设置最大反射次数为5次, 即如果某条射线经过5次反射后仍未被接收端接收到, 则将其丢弃不再跟踪.假设所有反射体的相对介电常数和电导率相同, 不同空间角度的发射和接收射线对应的天线增益根据图4中天线的辐射方向图决定.

表2 射线跟踪仿真参数设置 Tab.2 System parameters in ray tracing simulation

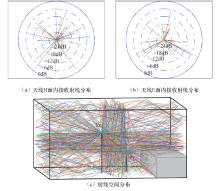
选取报告厅场景中用户C₃位置, 射线跟踪仿真与实测结果对比如图8所示, 图8(a)和图8(b)中分别为以接收天线的H面和E面为参考平面观察到的射线空间分布情况, 而图8(c)中展示了三维空间内的所有射线.

	Figure Option View Download New Window
	图8 用户C₁位置射线跟踪仿真结果示例Fig.8 Ray tracing simulation results for user C₁

从图8中可以看到, 水平面内多径分布较为均匀, 但是垂直面内多径分布集中在特定方向上, 并不均匀.垂直面内多径分布主要受到两个因素影响:一是天线辐射方向性, 二是房间尺寸与收发天线相对高度等环境因素.在垂直面内俯仰角较大的多径分量对应的天线增益比主瓣的增益会降低10 dB以上, 在接收端变得十分微弱.同时, 由于报告厅的长和宽远大于其高度, 并且收发天线存在高度差, 在垂直面内多径信号的到达方向会受到限制.这两个主要因素导致垂直维度内对接收天线可见的多径分量分布不均匀.因此, 天线阵列在垂直维度内扩展时, 相邻阵元之间信道变化减弱, 阵元相关性较高.这是造成水平面和垂直面内信道相关性差异的主要原因.

3.3 阵元信道相关系数拟合分析

为分析不同空间维度内阵元信道相关系数随阵元间隔的平均变化情况, 下面将不同用户位置以C₁~C₆和D₁~D₆进行分组, 在不同空间维度内进行拟合分析.

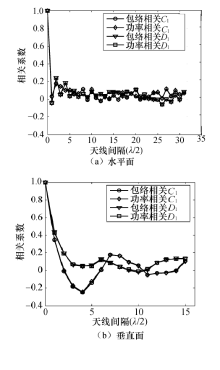
在水平面内, 不同用户位置对应的阵元信道相关系数平均水平差别较小, 均随阵元间隔增加呈现快速下降趋势.因此水平面内可用负指数衰减模型拟合, 所得拟合曲线和参数见图9所示.两种用户分布下的阵元相关系数对应的拟合负指数衰减模型参数较为接近, 稍大于d₀ (λ /2).

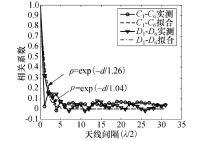	Figure Option View Download New Window
	图9 水平面内不同用户分布条件下阵元信道相关系数拟合Fig.9 Average antenna correlation coefficients fitting among different user distribution in horizontal plane

在垂直面内, 不同用户位置对应的信道相关系数随阵元间隔的变化均呈现比较明显的周期性, 这在图5和图6中十分显著. 因此在拟合建模时不再区分集中或分散用户, 而是针对每个用户位置分别进行分析.

通过分析垂直面内每个用户位置的阵元相关系数随阵元间隔的变化规律, 可以发现其波动性明显而且周期较长, 这与文献[8]中介绍的多种阵元相关模型的变化规律均有区别. 与Jakes模型相比, 实测相关系数曲线波动幅度较小; 而与sinc函数相比, 实测相关系数曲线下降速度更快. 因此两个模型均不能很好地对实测结果进行拟合. 经过多种函数拟合分析, 可以发现以下负指数衰减余弦函数可以较好地反映垂直面内实测相关系数曲线的特点

$R (d) = a^{d} \cos (b \cdot d) (12)$

式中:a和b为模型参数, 且a< 1; d为阵元间隔(单位d₀ = λ /2), 均为正实数.

此函数中前面的负指数衰减项决定相关系数随阵元距离的衰减速度, 后面的余弦项反映相关系数的变化周期. 当b→ 0时, 此模型退化为负指数函数.实际上, sinc函数与此模型较为相似. 它的分子项为正弦函数, 具有周期变化性质, 而分母为阵元间隔d的幂函数, 引入了相关系数随阵元间隔的衰减.但是, 幂函数的衰减速度小于负指数函数, 因此sinc函数的衰减速度小于式(12)中的模型.

使用此函数对实测相关系数曲线进行拟合, 得到模型参数.报告厅内选取距离较大的C₁与D₆位置, 拟合结果如图10所示. 可以看到C₁处的模型拟合效果较好, D₆处的模型在起始阶段比实际结果偏高, 之后两者逐渐一致.

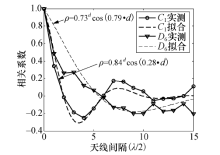	Figure Option View Download New Window
	图10 垂直面内特定用户位置阵元信道相关系数拟合Fig.10 Antenna correlation coefficients fitting for fixed user positions in vertical plane

为了更好地分析垂直面内阵元相关系数的特点, 在表3中列出了各个用户位置的建模结果对应的模型参数(C₅与D₄数据不完整, 未处理). 从表3中可以看到, 密集分布且离基站距离较近的用户, 对应的相关模型中a与b均较高且比较稳定, 说明相关系数随阵元间隔增加的下降速度较慢且变化周期较短. 分散用户的模型参数变化较大, 相关系数变化周期较长. 这主要是因为收发距离越大时, 垂直面内阵元相关系数受到天线辐射方向性的影响越小, 波动变化越不显著. 对所有用户位置的模型参数取平均值, 可知垂直面内阵元相关系数随阵元间隔的平均变化周期为5.7λ . 当阵元相关系数下降到0.5时, 对应的平均天线阵元间隔为0.6λ .

表3 垂直面内各用户位置对应的衰减余弦阵元相关模型参数 Tab.3 Parameters in the damped cosine correlation model for all users positions in vertical plane

4 用户信道相关性

多用户系统的信道容量与多用户之间的相关性(或正交性)密切相关.用户信道相关系数只能表征两个用户之间的信道相关性, 而多用户信道矩阵条件数则可同时反映多个用户子信道的正交性, 因此更适合多用户场景.从信道相关系数式(4)可以看到, 分母中有两个向量的方差, 其作用是对两个向量均做了归一化, 因此1.2节的不同信道归一化方法对信道相关系数影响不大, 在下面的分析中不做讨论.但是多用户信道矩阵条件数直接由信道矩阵得到, 不同的信道归一化方法会对结果产生较大影响.下面分别进行分析.

4.1 用户信道相关系数

分析实测室内场景中不同用户之间的信道相关系数.针对用户对基站阵列中各个阵元天线的信道增益向量H_k_,_l∈ $C^{N_{r} \times 1}$ (N_r为选定的基站天线数量), 由式(4)计算任意两个用户的信道相关系数, 并将所有子载波上的计算结果取平均.基站阵列中阵元数量从8开始, 每次增加4根天线, 直到该空间维度内最大天线数量(水平面内64, 垂直面内32).

为显示不同空间分布用户之间的信道相关性, 图11中给出了用户位置C₂与C₃和C₂与D₁之间在水平面和垂直面内的信道相关系数.C₂与C₃之间距离为0.53 m, 而C₂与D₁之间距离为4.59 m, 这两组结果可以表明不同用户距离对信道相关性的影响.

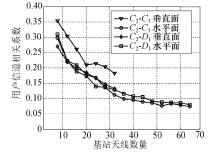	Figure Option View Download New Window
	图11 不同基站天线数量条件下的用户信道相关系数的绝对值Fig.11 User correlations (absolute value) under different BS antenna numbers

从图11中可以得到以下两个规律:

1)垂直面内的信道相关系数整体高于水平面内, 密集分布用户尤为明显, 分散用户间不显著; 不同用户之间在垂直面内的信道相关系数差异较大.

2)水平面内用户信道相关系数与用户距离关系较小; 基站阵列中阵元数量超过30之后, 用户信道相关系数随天线数量增加而下降缓慢, 此时再增加天线对降低用户信道相关系数作用不大.

第1个现象的主要原因在于, 在垂直面内, 当两个用户与基站距离较近时, 垂直极化天线增益的方向性影响较大, 使得部分散射分量的衰减较大. 此时信道中有效反射分量较少, 它们对于距离较近的用户变化较小, 因此两个用户的信道相关性较高. 当用户离基站距离较远(如D₁)时, 天线增益的方向性影响减弱, 可接收到更多散射多径分量, 因此用户信道相关性下降.

4.2 多用户信道条件数

多用户信道的相关性涉及在空间内分布的多个不同用户, 且信道条件数的计算采用多用户信道矩阵, 受到不同用户大尺度衰落的影响会比较大.同时, 大规模天线系统中阵列尺寸上也存在不同阵元间的大尺度衰落. 它们的影响可以通过第1.2节所述的不同信道归一化方法进行分析.

4.2.1 大尺度衰落的影响

利用水平面内基站阵列为64天线时的实测信道数据, 分别选取所有的任意3个和6个用户组合, 在每个子载波上, 获得多用户信道矩阵H_l∈ C^{64× (3, 6)}. 然后计算条件数, 并对所有子载波上的结果取平均, 得到各个用户组合的信道条件数, 其倒数的累积分布曲线如图12所示.

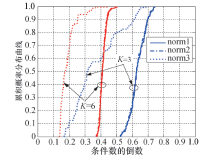	Figure Option View Download New Window
	图12 不同信道归一化方法的多用户信道条件数累积分布曲线Fig.12 Cumulative distribution curves for multi-user channel condition number under different channel normalizations

可以看到, 在不同的用户数量下, 第1种和第2种信道归一化方法(即norm1与norm2)获得的结果几乎相同, 这说明阵列尺寸上的大尺度衰落对多用户信道正交性的影响有限, 尤其是在阵列规模较大的情况下. 但是第3种信道归一化方法获得的结果偏小很多, 表明此时多用户信道正交性较差. 主要原因在于第3种信道归一化方法(即norm3)保留了不同用户之间的大尺度衰落. 这样距离近的用户到基站的信号明显强于距离远的用户, 各用户子信道差别较大, 导致R_tx的最大特征值与最小特征值相差较大.另外两种信道归一化方法消除了不同用户之间的大尺度衰落, 故不存在此问题. 图12中K=3和K=6分别对应3用户组和6用户组.

4.2.2 不同阵列天线数量和空间维度的影响

根据大规模天线系统渐近理论, 当基站天线数量趋于无穷时, 多用户之间的信道逐渐正交, 系统容量可随着用户数量增加而线性增加.实际无线环境中多用户信道之间存在一定相关性, 尤其是在室内场景用户距离较近的情况, 这会限制系统容量.多用户信道的正交性与用户数量、基站天线数量直接相关.图13显示两个空间维度内3种信道归一化条件下的结果. 可观察到以下规律:1)随着基站天线数量增加, 多用户信道正交性不断提高.基站天线数量超过30后, 条件数倒数增加幅度变缓, 但仍继续增加(尤其是norm1与norm2).2)norm1与norm2对应的信道正交性在不同空间维度内几乎相同, 而norm3对应的信道正交性在垂直面内高于水平面内.

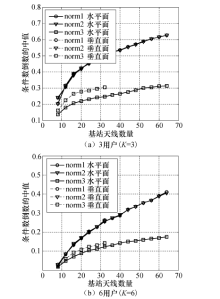	Figure Option View Download New Window
	图13 不同信道条件下多用户信道条件数倒数的中值变化Fig.13 Median change of the reciprocal number of multi-user channel conditions under different channel conditions

第1点说明基站天线数量的增加会持续改善多用户的信道正交性, 在实际无线环境中不断接近理想传输条件. 第2点规律较为特殊, 说明信道中存在的用户间大尺度衰落在不同空间维度内有较大差别. 为了对用户间大尺度衰落对信道正交性的影响做定量分析, 对应于图13中的结果, 表4中列出norm2与norm3对应的信道条件数倒数的比值, 即(Cond^norm2)^-1/(Cond^norm3)^-1. 从表4中可得出结论:

1)水平面内(Cond^norm2)^-1/(Cond^norm3)^-1整体大于垂直面内. 这说明水平面内多用户信道之间的大尺度衰落比垂直面内更严重, 将其影响消除后可取得更多的增益.

2)在两个空间维度内, 多数情况下(Cond^norm2)^-1/(Cond^norm3)^-1均会随着基站天线数量增加而增大; 但是水平面内3用户时, 基站天线从32增加到64, 比值反而略有下降. 这说明基站天线数量与用户数量比值N/K超过一定门限之后, 再增加基站天线数量对多用户信道正交性提高的作用十分有限.

3)垂直面内, 6用户时(Cond^norm2)^-1/ (Cond^norm3)^-1更大, 而水平面内6用户对应的(Cond^norm2)^-1/(Cond^norm3)^-1随着基站天线数量增加逐渐反超3用户对应的比值. 首先, 垂直面内信道变化更小而一致性较强, 因此用户数量越大, 用户间相对的信道大尺度衰落越严重, 将其消除后对用户正交性的效果越明显. 其次, 水平面内信道衰落更严重, 只有基站天线数量足够多时用户间大尺度衰落的影响才能充分显现.

表4 不同信道条件对(Cond^norm2)^-¹/(Cond^norm3)^-¹的影响 Tab.4 Impact of different channel conditions on (Cond^norm2)^-1/(Cond^norm3)^-1

5 结论

本文通过大规模天线无线信道实际测量, 对室内场景的无线信道空间相关性及其影响因素进行了分析讨论, 得出以下结论.

1)水平面内阵元信道相关系数随阵元距离增加而近似呈负指数衰减, 在阵元间隔为0.5~0.75λ 内即会衰减到1/e以下. 但是垂直面内阵元相关系数随阵元间隔呈现振荡衰减, 可用负指数衰减余弦函数进行拟合, 平均变化周期为5.7λ ; 当阵元相关系数下降到0.5时, 对应的平均天线阵元间隔为0.6λ .

2)不同用户间的大尺度衰落对多用户信道正交性有显著负面影响, 而且水平面内用户间大尺度衰落比垂直面内严重.因此实际系统中需要进行用户功率控制已达到较为理想的整体性能.另外, 大规模天线阵列中不同阵元之间的小尺度衰落对多用户信道矩阵条件数的影响较小.

3)基站天线数量增加对多用户信道正交性及两用户信道相关性均有明显改善; 基站天线数量超过30以后, 改善幅度变小, 但是仍有较明显提升.

4)影响不同空间维度内信道空间相关性的主要因素是天线辐射方向性和无线场景配置. 全向天线在垂直面内增益的方向性使得俯仰角较大的多径分量衰减较大; 同时报告厅的长与宽远大于其高度且收发天线存在高度差, 可接收到的多径分量在垂直面分布并不均匀. 这两个因素导致垂直面内信道变化较为缓慢, 阵元相关性较高, 但多用户之间的相对大尺度衰落较小.

参考文献

文献列表

[1]	LARSSON E G, EDFORS O, TUFVESSON F, et al. Massive MIMO for next generation wireless systems[J]. IEEE Communication Magazine, 2014, 52(2): 186-195. [本文引用:1]
[2]	RUSEK F, PERSSON D, LAU B K, et al. Scaling up MIMO: opportunities and challenges with very large arrays[J]. IEEE Signal Processing Magazine, 2013, 30(1): 40-60. [本文引用:1]
[3]	刘留, 陶成, 卢艳萍, 等. 大规模多天线无线信道及容量特性研究[J]. 北京交通大学学报, 2015, 39(2): 69-79. LIU Liu, TAO Cheng, LU Yanping, et al. Research on the propagation condition and channel capacity for massive MIMO[J]. Journal of Beijing Jiaotong University, 2015, 39(2): 69-79. (in Chinese) [本文引用:1]
[4]	PAYAMI S, TUFVESSON F. Channel measurements and analysis for very large array systems at 2. 6 GHz[C]// IEEE 6th European Conference on Antennas and Propagation, 2012: 433-437. [本文引用:1]
[5]	LIU L, TAO C, MATOLAK D W, et al. Stationarity investigation of a LOS massive MIMO channel in stadium scenarios[C]// IEEE 82nd Vehicular Technology Conference, 2015: 1-5. [本文引用:1]
[6]	RAPPAPORT T S, SUN S, MAYZUS R, et al. Millimeter wave mobile communications for 5G cellular: it will work[J]. IEEE Access, 2013, 1: 335-349. [本文引用:1]
[7]	GAO X, EDFORS O, RUSEK F, et al. Massive MIMO performance evaluation based on measured propagation data[J]. IEEE Transactions on Wireless Communications, 2015, 14(7): 3899-3910. [本文引用:2]
[8]	ALNAJJAR K A, SMITH P J, WHITING P, et al. Size and array shape for massive MIMO[J]. IEEE Wireless Communication Letters, 2015, 4(6): 653-656. [本文引用:2]
[9]	JIANG L, JUNGNICKEL V, JAECKEL S, et al. Correlation analysis of multiple-input multiple-output channels with cross-polarized antennas[C]// 14th Asia-Pacific Conference on Communications, 2008: 1-5. [本文引用:2]
[10]	LAMAIRE R O, ZORZI M. Effect of correlation in diversity systems with Rayleigh fading, shadowing, and power capture[J]. IEEE Journal on Selected Areas in Communications, 1996, 14(3): 449-460. [本文引用:2]
[11]	HOYDIS J, HOEK C, WILD T, et al. Channel measurements for large antenna arrays[C]// IEEE 9th International Symposiumon Wireless Communication Systems, 2012: 811-815. [本文引用:1]
[12]	LI J, ZHAO Y, TAO C, et al. System design and calibration for wideband channel sounding with multiple frequency band s[J]. IEEE Access, 2017, 5(1): 781-793. [本文引用:1]
[13]	赵友平, 张静, 李金兴, 等. 基于改进射线跟踪法的隧道环境无线信道仿真[J]. 北京交通大学学报, 2014, 38(5): 12-18. ZHAO Youping, ZHANG Jing, LI Jinxing, et al. Simulation of radio channel in tunnels based on the enhanced ray-tracing algorithm[J]. Journal of Beijing Jiaotong University, 2014, 38(5): 12-18. (in Chinese) [本文引用:1]

2014

0.0

... 大规模天线系统(Massive,MIMO或Large-Scale Antenna Systems)是第5代移动通信系统的关键技术之一^[1] ...

2013

0.0

... 在理想传输条件下,当基站阵列中的阵元天线远大于用户数量时,不同用户子信道之间趋于正交,可以最大限度地提高系统容量^[2,3] ...

2015

0.0

... 在理想传输条件下,当基站阵列中的阵元天线远大于用户数量时,不同用户子信道之间趋于正交,可以最大限度地提高系统容量^[2,3] ...

2012

0.0

... 测量场景涵盖城区室外、室内到室外及体育场等多种环境^[4,5],测量频段也覆盖了0~6 GHz的低频段和6 GHz以上的高频段(如毫米波频段)^[6] ...

2015

0.0

... 测量场景涵盖城区室外、室内到室外及体育场等多种环境^[4,5],测量频段也覆盖了0~6 GHz的低频段和6 GHz以上的高频段(如毫米波频段)^[6] ...

2013

0.0

... 测量场景涵盖城区室外、室内到室外及体育场等多种环境^[4,5],测量频段也覆盖了0~6 GHz的低频段和6 GHz以上的高频段(如毫米波频段)^[6] ...

2015

0.0

... 文献[7]发现紧致型天线阵列(如圆柱阵)由于阵元间隔较小,导致阵元相关性较高,信道容量降低 ...

... 2)norm2是保留某个用户对基站阵列中不同天线阵元上的功率变化,但是消除不同用户之间的大尺度衰落,具体过程为^[7] ...

2015

0.0

... 文献[8]比较了均匀面阵和均匀线阵的信道容量,发现阵元相关模型的衰减速度与单调性对信道容量影响显著 ...

... 通过分析垂直面内每个用户位置的阵元相关系数随阵元间隔的变化规律,可以发现其波动性明显而且周期较长,这与文献[8]中介绍的多种阵元相关模型的变化规律均有区别 ...

2008

0.0

... 1 信道相关系数针对第k个用户对基站阵列中不同阵元在多个子载波上的信道增益向量,定义基站阵列中各个阵元之间的信道包络相关系数为^[9] ...

... 文献[9]利用室外场景的MIMO测量数据,在视通(Line of Sight, LOS)和非视通(None Line of Sight, NLOS)两种条件下对文献[10]中的结论进行了验证,结果表明两者确实近似相等 ...

1996

0.0

... 根据文献[10]中的理论分析,假设阵列中两个阵元上的接收信号包络服从瑞利分布,它由一个联合高斯分布过程产生,则信道包络相关系数和功率相关系数均可由此联合高斯分布的协方差导出,并且最终可证明二者近似相等 ...

2012

0.0

... 0,则可定义条件数为^[11] ...

2017

0.0

... 关于测量系统的详细原理参见文献[12] ...

2014

0.0

... 仿真的具体过程可参见文献[13] ...