引用本文
罗艺, 钱大琳. 基于权重调整的公交网络效率研究[J]. 北京交通大学学报, 2018,42(1): 81-86.
LUO Yi, QIAN Dalin. Research of weight adjustment on the efficiency of transit networks[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2018,42(1): 81-86.
Doi:10.11860/j.issn.1673-0291.2018.01.012  
Permissions
Copyright©2018, 北京交通大学学报编辑部
北京交通大学学报编辑部 所有
基于权重调整的公交网络效率研究
罗艺, 钱大琳
北京交通大学 城市交通复杂系统理论与技术教育部重点实验室, 北京 100044

第一作者:罗艺(1983—),男,贵州贵阳人,博士生.研究方向为城市交通工程.email:lyiheart@bjtu.edu.cn.

收稿日期: 2017-04-22
基金: 北京市哲学社会科学规划重大项目(11ZDA03)
摘要

公交网络效率的高低关系着城市客运工作能否通畅有序运行.任意站点间的客运效率与整个公交网络的客运效率是局部与整体的关系,如何以最合理的局部效率改善达到提升整个公交网络效率的目的,是当前一项重要的研究课题.公交站点网络是无标度网络,网络边上的权重可表征站点之间的通行时间,调整边权重成为改善公交网络效率的途径之一.本文从宏观网络的角度,基于权重维度,研究权重在无标度网络中的不同分布对网络效率的影响.通过对权重在无标疫网络中作用的验证,为公交网络的优化提供新的指导方法.

关键词: 交通运输工程; 影响分析; 权重分布; 公交专用道; 复杂网络
中图分类号:U491.1 文献标志码:A 文章编号:1673-0291(2018)01-0081-06
Research of weight adjustment on the efficiency of transit networks
LUO Yi, QIAN Dalin
MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology, Beijing Jiaotong University, Beijing 100044, China
Fund:Foundation item:Major Projects in Beijing Philosophical and Social Science Program (11ZDA03)
Abstract

Efficiency of transit networks is often critical to the operations of urban transportation. Transport efficiency between any bus stations and that in the transit network are both on the relation between the part and the whole. How to improve the efficiency of the whole transit network by adjusting local efficiency is a very important research project. Bus station network is scale-free network. Link weight is the travel time between any stations. Therefore, the adjustment of weight becomes one of the methods to improve the efficiency of public transport network. From the perspective of network, the effects of weight distribution on the scale-free networks efficiency are investigated. The results demonstrate that exponential distribution of link weight shows significant improvement to the efficiency of transit networks in both global and local. This paper could provide a new guidance for the optimization of public transport network, through the role of weights in scale-free network is verified.

Keyword: traffic engineering; influence analysis; weight distribution; bus lanes; complex networks

城市公交网络效率是城市中绝大部分出行者, 尤其是通勤出行者的保障.近年来, 全国各大城市机动车保有量急剧上升, 不仅使得城市道路交通越发拥挤, 也严重影响了地面公共交通的通畅运行.因而各大城市采取了诸如开设公交专用道、对社会车辆限流、限号等措施, 以确保公交优先的发展策略.公交网络是由站点和站点之间的联系所组成, 所有站点间的客运效率共同构成了整个公交网络的效率, 提升公交网络效率是交通管理部门的重要目标之一.但对于整个网络来说, 以提高所有站点间的客运效率达到提高整个公交网络的效率是不现实也不妥当的.一方面需要投入巨大的资源, 另一方面会使得社会车辆的出行空间越发拥挤, 引发更为严重的道路拥堵.因此, 需要从网络的角度, 着眼于局部与整体的关系, 研究如何有针对性地改善相关站点间的客运效率以达到最大化整个公交网络效率的目的.

目前针对改善公交网络效率的研究文献已有不少[1, 2], 但一般是分析网络效率的影响因素和优化措施, 较少从网络角度揭示公交网络效率的整体与局部关系.研究证明, 公交站点网络具备复杂网络的结构特性, 是典型的无标度网络[3, 4].复杂网络是许多复杂系统相互作用结构的抽象, 可以仅由点和边构成的二元网络对其进行抽象.以节点表示元素, 连线表示节点间的关系, 连线上的权重表示元素之间的关系程度.故而我们也可以通过二元的点线关系获得公交网络的拓扑结构[4] (如节点表示站点, 节点间连线表示线路).一般来说, 进行公交网络站点间效率的调整, 并不会改变公交网络静态结构[5], 仅改变站点之间公交车辆的运行速度、发车频率等.近年来, 针对公交加权复杂网络的相关研究也很丰富, 2016年, 文献[6]基于Space L方法对北京市的公交加权网络的复杂特性进行实证分析, 从复杂网络的角度提出一种双层演化模型以模拟公交线路的发展; 2017年, 又进一步基于Space R方法就北京市的公交加权流量网络(Flow-weighted Transit Route Network, TRN)进行实证分析, 发现2011年和2015年北京市的TRN均具有无标度网络特性[7].

本文作者从宏观网络的角度, 基于公交站点网络及网络效率计算模型, 研究公交网络中权重的不同分布对公交效率的影响.以期通过本研究, 提升对专用道与公交网络效率关系的认识, 并对今后网络优化提供一定的参考.

1 公交网络拓扑及效率
1.1 公交网络拓扑

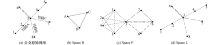
根据已有的研究可知, 获取网络拓扑结构可采用Space P、L、R三种方法[8].其中, Space P方法获取的网络结构称为公交换乘网络, 其将公交站点视为节点, 若站点之间有直达的公交车次, 则节点之间有连边; Space L方法获取到的是公交站点网络, 其同样将公交站点视为节点, 若两个站点地理位置相邻且有同一个车次通过, 则节点之间有连边; Space R方法则是用节点表示公交线路, 线路间有公共停靠站则有连边, 称为公交线路网络.三种方法各有特点, 公交站点网络既保留了原网络的拓扑性质, 同时又较好地体现了网络中站点之间的空间逻辑关系; 公交换乘网络能够更好地表示及研究公交网络中乘客的换乘状况; 公交线路网络则更多用于线路研究.图1分别给出了3种方法的相关示意图, 其中数字表示站点编号, 字母表示线路名称.

图1 公交网络拓扑结构Fig.1 Three topologies of transit network

本文的研究主要针对直观的公交网络拓扑, 研究站点之间的出行状况, 并不涉及公交换乘及线路关系, 因而采用Space L方法获取网络拓扑结构比较合适, 并用连边上的权重表示任意站点的出行时间.

1.2 公交网络效率

网络效率是用于衡量网络传输信息能力的指标.一般来说, 网络中两个点之间距离越近, 信息在这两点间传输就越容易.于是 i、 j两点间的效率 eij可以等于这两点间距离 dij的倒数, 即 eij=1/dij.若这两点之间不连通, 则可认为两点间距离为无穷大, 其效率为0.将网络中所有节点对的效率取平均即得到网络的全局效率如下

E=1NN-1∑i, j∈V, i≠jeij=1NN-1∑i, j∈V, i≠j1dij(1)

式(1)即是文献[9]提出的网络效率的定义, 此模型是针对相异权和无权网络提出的.在公交网络效率的计算中, 本文用任意两个站点 i、 j之间的通行时间 Tij替代式(1)中的 dij, 得到公交网络效率为

Et=1NN-1∑i, j∈V, i≠jeij=1NN-1∑i, j∈V, i≠j1Tij(2)

式中 N表示公交站点数量.

同样地, 可以计算出公交网络局部效率如下

Eloc=1N∑i∈GEGi(3)

式中: Gi是节点 i的近邻, 即是同节点 i直接相连的节点集合; EGi是节点 i近邻的网络效率, 用式(1)即可计算.

2 权重分布对公交网络效率的影响

开设公交专用道, 通常情况下, 在一定时期内并不会引起相关站点间客运总量发生较大变化, 最明显的改变是缩短了相关站点之间公交车辆的出行时间.因此, 根据第1节所述, 可认为该过程改变了公交网络中相关节点间连线的权重.研究表明:权重的分布会影响网络的结构和动力学行为, 如权重的重新分布可以改变网络的最短距离、聚类系数, 还能够影响网络的同步能力及社团结构的划分等[10, 11].因此, 利用权重这个维度及其在网络中的不同分布, 便可分析相关站点间客运效率改变后, 对公交网络效率产生的不同影响.

对网络权重进行调整的方式为:1)保持每一份权值不变, 即权重的分布形式固定, 改变权重和边的对应关系; 2)保持权重的总量或均值不变, 改变权重的分布形式.显然, 根据公交网络的特性, 本研究采用后者.

2.1 网络拓扑结构与效率

文献[12]在对波兰22个城市公交网络的研究, 文献[3, 4]对北京、廊坊、济宁、大连等城市的调研中均证明了公交站点网络具有幂律特性, 是典型的无标度网络.这些城市规模不同, 其中的公交站点数量从152个到2 811个不等, 且幂指数范围基本保持在(2, 3)之间.如图2中, 本文首先假定节点间权重为常数, 构建了50个节点数 N=1000且幂指数各不同的无标度网络, 以研究幂指数与网络效率的关系.

图2 幂指数变化下的效率Fig.2 Efficiency with the change of power law

由图2可见, 随着幂指数的不断变化, 网络的全局效率与局部效率变化很不明显, 进一步计算得幂指数与全局效率、局部效率的相关系数分别为-0.03和0.09, 可见幂指数的大小与网络效率没有明显关系.同样, 图3中, 令节点间权重和幂指数为常数, 研究节点数与网络效率的关系.

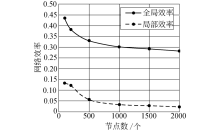图3 权重和幂指数不变下网络效率与其规模的关系Fig.3 Efficiency with the change of network size when weight and power exponent are constant

由图3可见, 随着节点数量的不断增加, 网络的全局与局部效率均逐步降低且下降速率逐渐趋缓.这说明规模较大的城市, 完成输送任务所需的耗费必定大于小规模城市.计算得节点数目与全局、局部效率的相关系数分别为-0.878和-0.851, 可见节点数量的多少与网络效率有很明显的负相关.

通过如上的研究可见, 网络效率与幂指数没有相关关系, 但会随着网络规模的扩大而逐渐降低.表明一个城市的地面公交网络规模必须要有所控制, 站点的增加、覆盖范围的扩大不仅需求更多的资源, 还可能导致公交网络的运输效率下降.于是优化公交网络及大力发展轨道交通, 便成为城市规模发展到一定程度后的主要工作方向.

2.2 不同权重分布对网络效率的影响

为考察权重的不同分布对公交网络效率的影响, 本文基于BA无标度网络的拓扑结构, 研究不同分布的权重对网络效率的影响.其中, 假定公交网络中任意站点间的客运量为固定常数, 于是站点间出行时间的改变即导致权重变化.权重随机分布的过程如下[11]:

1)假设初始每条边有相同的权重, 如 ω=6.令 ω> 1不但方便后续抽取权重, 也免于权重归一化后成为无权网络.

2)初始化 Δω的值, 将每条边的权重 ω均分为 ω/Δω份.

3)将所有的边按照概率 P随机抽取每份权重, 然后把抽取出来的所有权重再等概率地随机赋回到每条边上.

在整个过程中, 要求每条边必须至少拥有一个单位的权重, 以确保网络本身的拓扑结构不被改变, 若该边仅剩下一单位权重, 便不再抽取权重.另外还需保证网络的总权重不变, 一方面便于做前后比较, 另一方面也保证了网络效率的提高并不是以提高成本为代价.本文在节点数 N=1000, 幂指数 γ≈2.5的无标度网络中, 以概率 P从0.1到0.9将权重在网络中进行随机化分布模拟, 结果如图4所示.在计算机数值模拟中, 本文给出的结果是50次随机实验的平均, 以减小随机因素导致的涨落.如此便得到了权重在网络中的随机分布形式.

图4 随机化权重前后网络效率变化曲线Fig.4 Change of efficiency with randomization of weight

由图4明显可见, 权重随机化后, 无标度网络的全局、局部效率都得到一定提升.随着随机化概率的单调递增, 全局、局部效率并非单调变化, 如本文的实验网络在随机化概率为0.6左右两者可得到最大值.这是由于无标度网络本身就具有严重的异质性, 其各节点之间的连接状况(度数)具有严重的不均匀分布性, 整个网络中仅有少数节点是hub节点, 拥有较大的度数, 其余绝大部分节点度较小.hub节点连边的特性是边介数很大, 所以, 针对hub节点连边的权重改变, 相比于其他非hub节点连边权重的改变来说, 显然前者对网络效率的改变会更大.但是要注意, hub节点在网络中仅占少数, 因此权重随机化若要得到最优的网络效率, 必须要结合无标度网络特性.

通过上述内容也了解到, 权重在无标度网络上的异质性可以导致网络效率的提升, 因此权重异质性可以作为提升公交网络效率的一个参考方向, 也从此角度上证明了如公交专用道施划等工作对整个网络效率的贡献.

由上述研究结果可知, 权重在网络中的异质性对网络效率的提升有一定影响.就如同专用道在公交网络中的施划使得公交网络权重呈现出异质性.现实中, 交管部门会根据不同出行状况在相应站点之间施划公交专用道, 这些专用道在公交网络中的分布并不一定是随机分布, 因此我们有必要研究其他权重分布形式对网络效率的影响.

方法同上, 只是以不同的概率将每份权重放回到网络各边上, 以形成不同的权重分布.整个过程中仍然必须保证不同形式的分布权重的总和是相等的.本文在节点数为500、1 000、1 500、2 000, 幂指数 γ≈2.5的无标度网络中, 分别基于指数分布、泊松分布和均匀分布进行研究, 得到的结果如图5所示.

图5 不同权重分布的网络效率图Fig.5 Efficiency of network with different weights distribution

由图5可见, 随着网络规模的增大, 网络效率仍然逐渐下降.3种分布中, 指数分布对网络的影响最大, 得到的网络效率最高.

综合上述不同分布对网络效率的影响研究得知, 相对于权重平均后的公交网络来说, 仅调整权重分布就可使网络效率得到提高.可见相比较于改变公交网络拓扑结构而言, 调整权重成为一种提高网络效率的更为切实可行的办法, 也突显了公交专用道施划的必要性与可行性.此外, 也证明了不同的权重分布对于网络效率的改变是不一样的, 而公交网络的效用理应放到网络的范畴中进行研究分析, 也为今后公交网络规划研究提供了一个思路.

3 应用

基于上述研究结论, 本文作者通过相关城市的公交信息网站获取到了北京市的516条公交线路、成都市的220条公交线路及青岛市的129条公交线路等数据.利用Pajek绘制出的北京市公交站点网络拓扑结构示意图如图6所示.

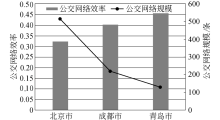
图6 公交站点网络示意图Fig.6 Topological diagram of public transportation station network

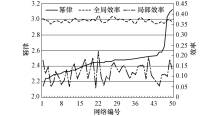
如图6可见, 该网络具有较为明显的模块性, 其中小部分节点集聚程度高, 大部分集聚程度低, 具有无标度网络性质[12].利用百度地图获取上述3座城市中两两站点间的实际道路长度, 并设公交车辆自由行驶速度 v=45 km/h[14], 计算出任意站点间的公交运行时间 T.根据式(2)计算出3座城市的公交网络全局效率, 如图7所示.

图7 三座城市的公交网络效率Fig.7 Transit efficiency of three cities

如图7可见, 公交网络规模越大, 站点数量越多, 站点间的出行时间越长, 则整个公交网络效率降低.分别基于随机分布、指数分布、泊松分布和均匀分布调整3座城市公交网络连边上的公交车辆运行时间 T.其中, 随机化概率 P取0.6, 得到网络效率的改善程度如图8所示.

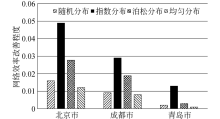图8 不同权重分布对三座城市的公交网络效率改善程度Fig.8 Improvement of transit efficiency in three cities with different weights distribution

图8中进一步验证了随机分布对网络效率的改善程度最为显著.此外, 权重异质化对北京市公交网络效率的改善程度最大, 青岛市最小.分析可知是由于城市规模越小, 任意站点间公交出行时间越短, 权重异质化后使得彼此差异并不大.且城市规模越小, 网络直径越小, 同样的时长范围内, 能够完成的客运工作量就越多.

4 结论

1)基于城市公交站点网络的无标度网络特性, 给出了公交网络客运效率的定义.基于权重维度, 以改变权重分布形式的方式, 考察无标度网络中权重的不同分布对网络的全局、局部效率所产生的影响.不改变网络结构及权重总值, 通过权重的异质性也能够实现网络效率的提升.

2)研究发现, 公交网络的全局、局部效率与幂指数的大小并没有关联, 但随着网络规模的扩大而逐渐降低.本文结果对于深入理解施划公交专用道等措施对公交网络结构与功能的影响提供了基础, 也证明了当前控制城市规模, 大力发展轨道交通的必要性.

The authors have declared that no competing interests exist.

参考文献
[1] 刘海伟. 城市公交加权网络模型及其应用研究[D]. 重庆: 重庆大学, 2015.
LIU Haiwei. Research on the model of weighted public transport network and its applications [D]. Chongqing: Chongqing University, 2015. (in Chinese) [本文引用:1]
[2] 田庆飞. 基于复杂网络理论的城市公交网络生成与优化研究[D]. 长春: 吉林大学, 2013.
TIAN Qingfei. Study on urban transit network generation and optimization based on complex network theory [D]. Changchun: Jilin University, 2013. (in Chinese) [本文引用:1]
[3] 高自友, 吴建军, 毛保华, 等. 交通运输网络复杂性及其相关问题的研究[J]. 交通运输系统工程与信息, 2005, 5(2): 79-84.
GAO Ziyou, WU Jianjun, MAO Baohua, et al. Study on the complexity of traffic networks and related problems[J]. Journal of Transportation Systems Engineering and Information Technology, 2005, 5(2): 79-84. (in Chinese) [本文引用:2]
[4] HUAPU L U, YE S. Complexity of public transport networks[J]. Tsinghua Science & Technology, 2007, 12(2): 204-213. [本文引用:3]
[5] 要甲. 基于多式交通均衡的公交专用道设置分析与优化[D]. 长沙: 中南大学, 2014.
YAO Jia. Bus exclusive lane setting analysis and optimization based on multi-modal transportation equilibrium [D]. Changsha: Central South University, 2014. (in Chinese) [本文引用:1]
[6] HUANG A, XIONG J, SHEN J, et al. Evolution of weighted complex bus transit networks with flow[J]. International Journal of Modern Physics C, 2016, 27(6): 1650064. [本文引用:1]
[7] HUANG A, ZANG G, HE Z, et al. Comparative empirical analysis of flow-weighted transit route networks in R-space and evolution modeling[J]. International Journal of Modern Physics B, 2017, 31(12): 1750087. [本文引用:1]
[8] 何大韧, 刘宗华, 汪秉宏. 复杂系统与复杂网络[M]. 北京: 高等教育出版社, 2010.
HE Daren, LIU Zonghua, WANG Binghong. Complex system and complex network [M]. Beijing: High Education Press, 2010. (in Chinese) [本文引用:1]
[9] LATORA V, MARCHIORI M. Economic small-world behavior in weighted networks[J]. Physics of Condensed Matter, 2002, 32(2): 249-263. [本文引用:1]
[10] 李岩, 吕翎, 栾玲. 环形加权网络的时空混沌延迟同步[J]. 物理学报, 2009, 58(7): 4463-4468.
LI Yan, LYU Ling, LUAN Ling. Lag synchronization of spatiotemporal chaos in a weighted network with ring connection[J]. Acta Physica Sinica, 2009, 58(7): 4463-4468. (in Chinese) [本文引用:1]
[11] LI D Q, LI M H, WU J S, et al. Enhancing synchronizability by weight rand omization on regular networks[J]. The European Physical Journal B, 2007, 57(4): 423-428. [本文引用:2]
[12] SIENKIEWICZ J, HOLYST J A. Statistical analysis of 22 public transport networks in Poland [J]. Physical Review E, 2005, 72(4): 046127. [本文引用:2]
[13] 罗艺, 钱大琳. 公交—地铁复合网络构建及网络特性分析[J]. 交通运输系统工程与信息, 2015, 15(5): 39-44.
LUO Yi, QIAN Dalin. Construction of subway and bus transport networks and analysis of the network topology characteristics[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(5): 39-44. (in Chinese) [本文引用:1]
[14] 左忠义, 杨广川, 邵春福. 基于公交优先的小汽车出行向公交转移模型研究[J]. 交通运输系统工程与信息, 2012, 12(1): 124-130.
ZUO Zhonyi, YANG Guangchuan, SHAO Chunfu. Modeling modal shift of car travelers to buses based on public transport priority[J]. Journal of Transportation Systems Engineering and Information Technology, 2012, 12(1): 124-130. (in Chinese) [本文引用:1]