引用本文
宋志坤, 岳仁法, 胡晓依, 李响. 车轮多边形对车辆振动及轮轨力的影响[J]. 北京交通大学学报, 2017,41(6): 88-93.
SONG Zhikun, YUE Renfa, HU Xiaoyi, LI Xiang. Influence of wheel polygon on vehicle vibration and wheel/rail force[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2017,41(6): 88-93.
Doi:10.11860/j.issn.1673-0291.2017.06.014  
Permissions
Copyright©2017, 北京交通大学学报编辑部
北京交通大学学报编辑部 所有
车轮多边形对车辆振动及轮轨力的影响
宋志坤1, 岳仁法1, 胡晓依2, 李响1
1.北京交通大学 机械与电子控制工程学院,北京 100044
2.中国铁道科学研究院 铁道科学技术研究发展中心,北京 100081

第一作者:宋志坤(1972—),男,安徽东至人,副教授,博士.研究方向为车辆动力学及结构疲劳强度.email:zhksong@bjtu.edu.cn.

收稿日期: 2017-01-17
基金: 中国铁路总公司科技研究开发计划重点课题(2017G011-C)
摘要

针对国内车轮多边形现象日益突出,应用ANSYS和SIMPACK软件建立考虑轮对柔性的车辆刚柔耦合系统动力学模型,研究车轮多边形对车辆振动及轮轨力的影响并提出不同阶次的车轮多边形限值.研究表明:轮轨垂向力波动随车轮多边形幅值的增大而增大,但不随多边形阶次的增加而线性增大;轮对弯曲振动频率会与轮对的侧滚与转臂的点头频率相耦合,如果由车轮多边形产生的振动频率在该频率范围内,将会产生共振;根据轮轨力上限值170 kN提出300 km/h速度下1~20阶车轮多边形波深限值,特别是11阶车轮多边形的波深不宜超过0.07 mm.

关键词: 动力学; 多边形; 柔性轮对; 车辆振动; 轮轨力
中图分类号:U260.11 文献标志码:A 文章编号:1673-0291(2017)06-0088-06
Influence of wheel polygon on vehicle vibration and wheel/rail force
SONG Zhikun1, YUE Renfa1, HU Xiaoyi2, LI Xiang1
1. School of Mechanical, Electronic and Control Engineering, Beijing Jiaotong University, Beijing 100044,China
2.Railway Science & Technology & Development Center, China Academy of Railway Sciences, Beijing 100081, China;
Fund:Science and Technology Research and Development Program of China Railway Corporation(2017G011-C)
Abstract

For the polygonal wheel phenomenon becoming increasingly prominent, a rigid-flexible coupling vehicle system dynamics model is established in ANSYS and SIMPACK considering the flexible wheelset. The influence of polygonal wheels on the vehicle vibration and the wheel rail contact force is studied. The results show that the fluctuation of the wheel/rail vertical force increases with the increase of the polygon wave depth, but does not increase with the increase of the polygon. The bending vibration frequency of the wheel pair can be coupled with the nod frequency of the wheel set and the rotating arm. If the vibration frequency generated by the polygon of the wheel is in the range of the frequency, the resonance will occur. According to the wheel/rail force upper limit value 170 kN, the 1~20 polygon wave depth limit value at the speed of 300 km/h is proposed, especially the wave depth of the 11 wheel polygon is smaller than 0.07 mm.

Keyword: dynamic; polygon; flexible wheel; vehicle vibration; wheel/rail force

车轮多边形属于车轮周向不均匀磨耗的一种形式, 也常称为车轮波磨或车轮周期性非圆化, 普遍存在于地铁车辆、普通铁路及高速列车运营中.车轮多边形会使车辆轨道系统之间的振动加剧, 对轨道和车辆部件产生严重损伤并增大轮轨冲击和滚动噪声, 尤其是在高速列车运行中, 车轮多边形对车辆安全运营构成了潜在威胁[1, 2].

针对车轮多边形现象, 国内外专家学者对其进行了大量的研究.文献[3]建立了ICE-1型车的车辆/轨道动力学模型, 研究了车轮多边形的发展规律及其对垂向轮轨接触力和线路响应的影响.文献[4]指出, 由于轮轴弯曲振动导致的轮轨间横向滑移增大了车轮踏面的不均匀磨耗, 从而导致了车轮多边形现象.文献[5]建立了柔性轮对的动力学模型并研究了车轮多边形对轮轴动应力的影响.文献[6]基于有限元的方法对车轮多边形磨耗机理进行了研究.文献[7]对高速车轮椭圆化下的车辆系统行为进行了研究.文献[8, 9]研究了多刚体动力学系统中, 车轮多边形对车辆动力学性能的影响.近几年来, 车轮多边形现象在我国出现得越来越频繁, 成为轮轨关系恶化的一大因素, 尤其是高阶车轮多边形在高速下引起的高频振动对轴箱、构架等车辆部件的破坏尤为严重, 故车轮多边形产生机理和控制措施的研究显得尤为重要.

本文作者以国内某型高速动车组为研究对象, 将其轮对考虑为柔性体, 并建立了车辆系统刚柔耦合动力学模型.分析了19阶车轮多边形在不同速度下及车轮多边形的不同波深、阶次对车辆振动及轮轨力的影响, 并提出了车轮多边形的波深磨耗限值.

1 车轮多边形数据分析

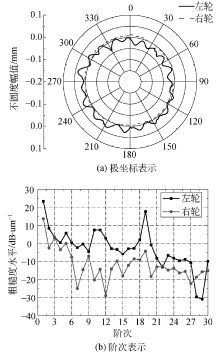
对车轮多边形磨耗情况进行了跟踪测试, 3车4轴位镟修后运行13.2万km时的测试结果如图1所示.

图1 车轮多边形测量结果Fig.1 Testing results of wheel polygon

由图1可得, 右轮磨耗正常, 左轮出现了明显的多边形现象.将车轮周向不圆顺数据进行傅里叶变换得到车轮多边形阶次分布, 右轮没有出现某阶次主导的多边形现象, 而左轮出现了以19阶次为主导的车轮多边形, 第10、11阶多边形也较为明显.

2 刚柔耦合动力学模型建立
2.1 柔性轮对模型建立

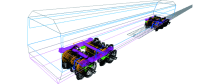
有限元模型及主节点选取如图2所示.轮对的主要模态信息如表1所示.

图2 柔性轮对Fig.2 Flexible wheelset

表1 车轮模态分析结果 Tab.1 Modal analysis results of wheelset

通过有限元分析软件ANSYS, 采用子结构的方法[10]建立轮对的柔性体模型, 并通过SIMPACK的接口模块FEMBS导入SIMPACK.将车轮踏面作为一个无质量的刚体并固定到车轮上.模型中忽略轮对的过盈配合, 即将轮对考虑成一个整体, 轮轴中部为空心结构, 在轴心及轴线两端距轴心1 m的地方建立质量很小的mass 21单元与周围节点进行刚性耦合.包括mass 21单元节点在内整个轮对模型共选取了225个主节点, 675个主自由度.

2.2 整车刚柔耦合动力学模型建立

首先建立车辆多刚体动力学模型, 然后把柔性轮对导入SIMPACK中替换原来的刚性轮对, 最终得到整车刚柔耦合动力学模型, 如图3所示.模型由1个车体、2个转向架、4个轮对和8个轴箱组成.其中, 车体、转向架和轮对均设置横向、垂向、纵向、点头、摇头、侧滚6个自由度, 轴箱设置1个转动自由度, 整车共有50个自由度.模型中各部件的质量、转动惯量参数, 一、二系悬挂参数及其他结构参数均根据该型车的实际参数进行设置.

图3 车辆动力学模型Fig.3 Vehicle system dynamic model

3 车辆动力学模型验证
3.1 车轴挠度

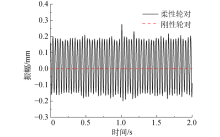
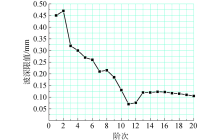
在车辆实际运行中, 轮对要承受轴箱及以上部件的重量, 这必然会导致车轴有少量的弯曲变形, 车轴中心不再处于理想位置.图4为车辆以京沪实测线路谱为轨道不平顺, 在300 km/h速度下行驶时车轴的挠度变化曲线.在考虑轮对柔性后, 随着车轮的滚动, 车轴中心位置在正负值之间变化, 而刚性轮对的车轴就不存在挠度变化的情况, 因此考虑轮对柔性后能更好地反映车轮的实际运动特征.

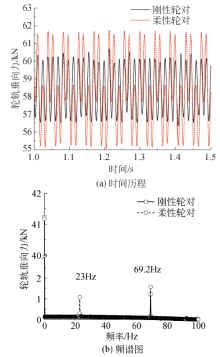
图4 轮对挠度时间历程曲线Fig.4 Time history curves of wheel deflection

3.2 轮轨垂向力

假设车辆在理想的平直轨道上以240 km/h行驶, 设置幅值为0.1 mm的三阶车轮多边形, 将刚性轮对与柔性轮对轮轨垂向力的计算结果进行对比分析, 如图5所示.

为方便观察, 图5(a)取1~1.5 s时的轮轨垂向力进行分析, 由图5(a)可以看出:考虑轮对柔性后轮轨垂向力的最大值由60.7 kN变为61.8 kN.由图5(b)可以看出:考虑轮对柔性的轮轨垂向力在23 Hz出现一个峰值, 该频率由轮对挠度变化引起, 69.2 Hz处柔性轮对的轮轨垂向力幅值比刚性轮对大, 这是由于该频率下引起轮对的一阶弯曲共振导致.由此可见, 考虑轮对柔性的轮轨垂向力计算结果与刚性轮对下差异明显.

图5 轮轨垂向力时、频曲线Fig.5 Time domain and frequency domain curves of wheel rail vertical force

4 仿真计算
4.1 多边形下的车辆振动及轮轨力

将车轮设置为幅值0.1 mm的19阶多边形, 分析车辆在50~350 km/h速度范围内轮对、转向架和车体的垂向加速度和轮轨力的变化情况, 结果如图6~图9所示.

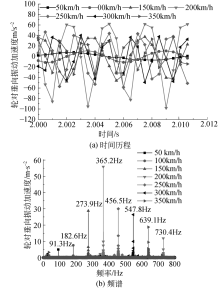图6 轮对垂向加速度时、频曲线Fig.6 Time domain and frequency domain curves of vertical vibration acceleration of wheelset

图7 构架垂向加速度时、频曲线Fig.7 Time domain and frequency domain curves of vertical acceleration of bogie

图8 车体垂向加速度时、频曲线Fig.8 Time domain and frequency domain curves of vertical acceleration of vehicle

图9 轮轨垂向力随速度变化曲线Fig.9 Wheel rail vertical force

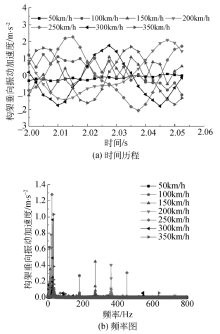
图6为第1轮对的垂向加速度达到稳定后的时间历程及频谱图, 为便于观察, 取2~2.012 s进行画图, 由图6(a)可知:当车辆在150 km/h以上的速度行驶时, 轮对垂向加速度波动明显增大, 尤其在时速200 km/h下轮对垂向加速度振动幅值可达107 m· s-2; 由图6(b)可以看出车辆行驶中由车轮多边形引起的中、高频率的垂向振动加速度峰值最高可达55 m· s-2.

图7为前转向架垂向加速度时间历程及频谱图, 为便于观察, 图7(a)取2~2.06 s进行分析, 可知:相对于轮对构架各速度等级下的垂向振动加速度幅值明显减小; 图7(a)可以看出:中、高频率的垂向振动加速度峰值明显减小, 最高为2.35 m· s-2.由此可见, 转臂跟一系悬挂对车轮多边形引起的振动有一定衰减作用.

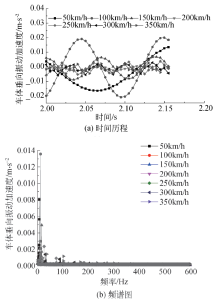
图8为车体垂向加速度时间历程及频谱图, 为便于观察, 图8(a)取2~2.2 s进行分析, 由图可知:50 km/h和100 km/h的垂向振动加速度幅值高于其他速度等级.由图8(b)可以看出:由车轮多边形导致的中、高振动频率的加速度峰值进一步被衰减, 而由轮对挠度变化引起的车体垂向低频振动仍然存在.

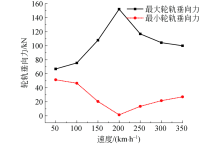
图9为轮轨垂向力最大值与最小值随速度的变化曲线.由图9可以看出:轮轨垂向力波动不完全随车辆运行速度的提高而增大.在200 km/h速度等级下的轮轨垂向力最大值达到了152.2 kN, 最小值1.4 kN, 轮轨垂向力波动最剧烈.

由不同速度等级下车辆各部件垂向振动加速度及轮轨垂向力的对比可以看出:在200 km/h的速度等级下轮对、构架垂向加速度和轮轨垂向力幅值均比其他速度等级高.这是因为在该速度等级下, 由19阶车轮多边形产生的轮轨冲击频率(365 Hz)与轮对的四阶弯曲模态频率(345 Hz)、轴箱点头运动和轮对侧滚运动的频率(312 Hz)相近, 从而使系统出现了共振现象.

4.2 车轮多边形幅值对轮轨垂向力的影响

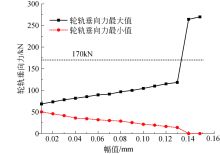
轮轨垂向力随波深变化曲线如图10所示.

图10 轮轨垂向力随波深变化曲线Fig.10 Curves of wheel rail vertical force under different polygon amplitudes

图10中假设车辆以300 km/h的速度在理想平直轨道上行驶, 设置车轮多边形阶次为19阶, 多边形的幅值从0.01 mm到0.15 mm逐渐增大, 通过计算得到轮轨垂向力与幅值变化的关系曲线.可以看出:轮轨垂向力最大值随着幅值的增大而增大, 轮轨垂向力最小值则随之增大而减小.当幅值超过0.14 mm后轮轨垂向力迅速增大到264.2 kN, 并会出现跳轨现象.

4.3 车轮多边形阶次对轮轨力的影响

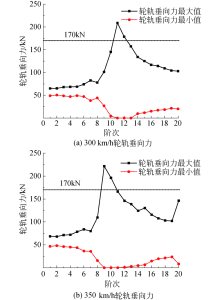
在300 km/h和350 km/h速度等级下, 设置车轮多变形的幅值为0.1 mm, 1~20阶车轮多边形下的轮轨垂向力最大值和最小值的变化情况见图11.

图11 轮轨垂向力随阶次变化曲线Fig.11 Curves of wheel rail vertical force under different polygon orders

由图11可以看出对于300 km/h时速, 轮轨垂向力最大值随着多边形阶次先增大后减小, 而对于350 km/h时速, 轮轨垂向力最大值随着多边形阶次先增大后减小, 但20阶多边形对应的轮轨垂向力波动增大.这是因为车辆系统在312 Hz附近存在较明显的轴箱点头运动和轮对侧滚运动模态.当车轮多边形产生的轮轨冲击频率与该振动频率接近时, 容易发生耦合, 引起系统共振, 使轮轨垂向力波动加剧.对于300 km/h时速, 当车轮多边形阶次由1阶增大到11阶时(11阶多边形产生的轮轨冲击频率为317 Hz), 与该振动频率越来越接近, 当多边形阶次由11阶增大到20阶时与该振动频率逐渐远离, 从而使得轮轨力波动出现先增大后减小的趋势, 并在11阶次下轮轨垂向力波动最大, 最大值达到208.5 kN.同理, 时速350 km/h在9阶车轮多边形下(产生的轮轨冲击频率为303 Hz与312 Hz最为接近)轮轨垂向力波动最大, 最大值达到221.5 kN.对于时速350 km/h, 20阶多边形产生的冲击振动频率, 与轮对的高阶弯曲模态及转臂点头运动频率(714 Hz)相靠近, 从而使轮轨垂向力波动增大.

4.4 波深限值

根据《高速试验列车动力学强度及动力学性能规范》(95J01-L)中动力学标准规定:轮轨垂向力限值不大于170 kN.计算速度300 km/h下1~20阶多边形幅值安全限值, 结果如图12所示, 由图可知:车轮阶次不同, 所对应的波深安全限值也不同, 阶次越高车轮多边形安全限值越低.在该速度的某些阶次下容易引发车辆部件共振从而使幅值限值进一步降低.

图12 300 km/h下车轮多边形波深安全限值Fig.12 Safety limit of wheel polygon amplitude under 300 km/h

5 结论

1)车轮多边形产生的频率较高的轮轨冲击造成较大轮对和构架垂向振动加速度, 车体垂向振动加速度较小; 轮对四阶弯曲频率与轮对的侧滚、转臂的点头频率相近, 容易产生共振.

2)300 km/h速度等级下, 19阶车轮多边形引起的轮轨垂向力波动随多边形幅值的增大而增大, 随多边形阶次的增大先增大后减小; 时速350 km/h轮轨垂向力波动随车轮多边形阶次的增加而呈现出先增大后减小再增大的趋势.

3)根据轮轨垂向力170 kN的上限值, 确定300 km/h速度下1~20阶车轮多边形波深限值, 特别是11阶多边形, 波深不宜超过0.07 mm, 可为列车车轮镟修提供参考.

The authors have declared that no competing interests exist.

参考文献
[1] BARKE D W, CHIU W K. A review of the effects of out-of-round wheels on track and vehicle components[C]//Proceedings of the Institution of Mechanical Engi-neers Part F Journal of Rail & Rapid Transit, 2005: 151-175. [本文引用:1]
[2] LIU X, ZHAI W. Analysis of vertical dynamic wheel/rail interaction caused by polygonal wheels on high-speed trains[J]. Wear, 2014, 314(1/2): 282-290. [本文引用:1]
[3] MORYS B. Enlargement of out-of-round wheel profiles on high speed trains[J]. J Sound Vib, 1999, 227(5): 965-978. [本文引用:1]
[4] JIN X, WU L, FANG J, et al. An investigation into the mechanism of the polygonal wear of metrotrain wheels and its effect on the dynamic behaviour of a wheel/rail system[J]. Vehicle Syst Dyn, 2013, 50(12): 1817-1834. [本文引用:1]
[5] WU X, CHI M, WU P. Influence of polygonal wear of railway wheels on the wheel set axle stress[J]. Vehicle Syst Dyn, 2015, 53(11): 1535-1554. [本文引用:1]
[6] 陈光雄, 金学松, 邬平波, 等. 车轮多边形磨耗的有限元研究[J]. 铁道学报, 2011: 33(1): 14-18.
CHEN Guangxiong, JIN Xuesong, WU Pingbo, et al. Finite element study on the generation mechanism of polygonal wear of railway wheels[J]. Journal of the China Railway Society, 2011, 33(1): 14-18. (in Chinese) [本文引用:1]
[7] 张雪珊, 肖新标, 金学松. 高速车轮椭圆化对车辆系统行为的影响[J]. 机械工程学报, 2010, 46(16): 67-73.
ZHANG Xueshan, XIAO Xinbiao, JIN Xuesong. Effect of ovalization of high speed railway wheels on vehicle dynamic performance[J]. Journal of Mechanical Engineering, 2010, 46(16): 67-73. (in Chinese) [本文引用:1]
[8] 吴磊, 钟硕乔, 金学松, 等. 车轮多边形化对车辆运行安全性能的影响[J]. 交通运输工程学报, 2011, 11(3): 47-49.
WU Lei, ZHONG Shuoqiao, JIN Xuesong, et al. Influence of polygonal wheel on running safety of vehicle[J]. Journal of Traffic and Transportation Engineering, 2011, 11(3): 47-49. (in Chinese) [本文引用:1]
[9] 陈伟, 戴焕云, 罗仁. 高速列车车轮高阶多边形对车辆动力学性能的影响[J]. 铁道车辆, 2014, 52(12): 4-8.
CHEN Wei, DAI Huanyun, LUO Ren. Influence of high-level polygonal wheel on dynamic performance of high-speed train[J]. Rolling Stock, 2014, 52(12): 4-8. (in Chinese) [本文引用:1]
[10] 包学海, 池茂儒, 卢耀辉, 等. 基于子结构法的车辆系统刚柔混合动力学建模方法研究[J]. 铁道机车车辆, 2009, 29(3): 8-13.
BAO Xuehai, CHI Maoru, LU Yaohui, et a1. Research on vehicle system dynamics model of rigid-flexible mixture based on substructure method[J]. Railway Locomotive & Car, 2009, 29(3): 8-13. (in Chinese) [本文引用:1]