第一作者:王文静(1976—),女,山东陵县人,教授,博士,博士生导师.研究方向为结构强度与疲劳可靠性. email:wjwang@bjtu.edu.cn.
针对传统名义应力整体法在焊接板结构疲劳分析应用中的实际困难,介绍和分析了应用于海洋结构工程领域的基于表面外推的热点应力法.通过对焊接样件在不同应力水平下的疲劳试验,获取了焊接样件在97.7%可靠度下的疲劳寿命.采用热点应力法计算样件焊趾处热点应力值,提出考虑主板厚度效应的修正S-N曲线,并预测了样件的疲劳寿命.结果表明:板厚修正后的热点应力S-N曲线应用于薄板焊接结构疲劳寿命评估具有更高的精度和可靠性.以轨道车辆用焊接天线梁为例,采用该方法分析了焊缝处的热点应力,其最大应力发生位置与线路运用中出现裂纹位置相吻合,其计算寿命为7.1×105次,与实际运营结果基本一致.为平板焊接接头的抗疲劳设计提供参考.
In view of the practical difficulies facing the traditional nominal stress approach applied in fatigue analysis of weld plate structure, the hot spot stress method based on the surface extrapolation is introduced comprehensively. It has been developed in marine structural engineering well. The specimens are loaded under different stress levels and the fatigue life with 97.7% reliability is obtained. The hot spot stress of the specimen weld toe is calculated by the spot stress method and the fatigue life is given by FAT90 modified S-N curve considering the plate thickness effect. The results show good accuracy and better reliability in the assessment of weld structure fatigue life. Taking the railway antenna beam as example, the hot spot stress method is used to get the maximum stress point, which is consistent with the fatigue crack position in service. The fatigue life prediction of the antenna is 7.1×105 and it coincides with the actual operation life basically. The analysis method can be applied on the anti-fatigue design of weld joints of plate structure.
长期以来, 在不同工业领域中钢结构焊接接头及部件细节的疲劳设计和强度评定主要采用基于材料力学的应力分析和以大量疲劳试验数据为基础的S-N曲线相结合的名义应力法[1, 2, 3], 但由于实际焊接结构几何形状和受力状态的复杂性, 很难从有限元分析中获得实际的名义应力[4].为了弥补名义应力法的不足, 一种主要针对结构焊趾处疲劳的局部分析方法— — 热点应力法于20世纪90年代初开始应用于平板焊接结构的疲劳性能分析中[5], 如海上浮式生产储存装置等.国内学者对热点应力法在焊接结构中的应用也开展了深入的研究.文献[4]中应用热点应力法对焊接货车转向架关键点进行疲劳强度分析, 探讨了热点应力的求解过程及应用条件.文献[5, 6, 7]对热点应力的概念及外推方法进行了详细阐述, 并研究了热点应力法在平板结构焊接接头中的应用.文献[8]比较了大量疲劳试验结果, 分析表明:FAT 90作为热点应力S-N曲线时需根据主板厚度进行必要修正.
本文作者通过疲劳试验分析研究了薄板焊接接头的疲劳性能, 并与有限元分析结果进行对比分析来获取板厚修正系数, 提出了修正热点应力S-N曲线.应用修正后的热点应力S-N曲线评估了焊接天线梁疲劳寿命.
紧靠焊趾缺口或焊缝端部缺口前沿的局部最大结构应力称为热点应力, 焊接结构的热点应力一般发生在焊趾处, 是疲劳裂纹的起始部位.焊接接头的热点应力可通过有限元和线性外推相结合的方式获得, 也可通过构件焊趾处的名义应力与相应的结构应力集中系数获得[5].对于受力较为复杂的结构, 后一种方法很难实现对天线梁焊趾处热点应力的求解, 因此, 本文作者采用热点应力的线性外推法.
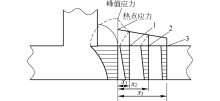
焊接板结构中, 热点应力是用距离焊趾“ 足够距离” 处两点或三点的表面结构应力外推得到, 所谓的“ 足够距离” 是指在这一距离处缺口效应不再发生影响, 结构应力基本成线性分布.其计算原理如图1所示.
利用图1中外推点的结构应力进行线性或二次插值计算来确定焊趾处的热点应力.表面线性及二次外推法的计算公式分别为
式中:σ hs为外推得到的焊趾处热点应力值; x1、x2、x3分别为外推点1、2、3与焊趾热点之间的距离; σ 1、σ 2、σ 3分别为外推点1、2、3处的结构应力值.
各国船级社推荐应用在距离焊趾0.5δ 和1.5δ (δ 为主板厚度)处测量应力值进行两点线性外推, 同时, 文献[9]对不同外推法进行了对比分析, 分析结果表明:应用外推点为0.5δ /1.5δ 推出的热点应力值具有较小的离散性.因此本文采用该外推法求解热点应力, 其公式为
式中:σ 0.5δ 和σ 1.5δ 分别表示距焊趾0.5δ 和1.5δ 处的应力值.
焊接天线梁在实际运营过程中, 其结构中的平均应力对材料的疲劳性能具有一定影响, 因此需要将实际的工作循环应力水平等寿命地转换为对称循环下的应力水平, 其等寿命转换公式为
式中:σ a为材料实际的应力幅值; σ m为材料实际的平均应力; σ -1为转换的等效应力; σ u为材料的抗拉强度.
焊接天线梁受各向加速度的作用, 局部焊缝焊趾处于复合应力状态.为得出沿焊缝垂直方向的结构应力, 需要将复合应力转化为一种单向的等效应力.根据文献[10]可知, 3个方向应力状态下的角焊缝焊趾处等效应力的计算公式为
式中:σ ceq为与焊缝垂直的单向等效应力; σ c为与焊缝垂直的应力分量; σ p为与焊缝平行的应力分量; τ p为焊缝所承受的剪应力.
对于焊接板结构的热点应力S-N曲线尚未有统一的数据, 各国船级社(如挪威船级社DET NORSKE VERITAS, DNV)组成的联合工业项目对热点应力S-N曲线的确定进行了大量试验, 经过综合分析及对比研究认为, 当采用20节点体单元建立有限元模型和距离热点0.5δ 和1.5δ 为参考点进行线性外推得到的热点应力时, 可应用FAT90作为一条通用的热点应力S-N曲线[11].FAT90所对应的S-N曲线具有97.7%的存活率, 该曲线考虑了焊接改进工艺、残余应力释放等因素的影响, 一般称为标准设计S-N曲线, 其相关参数为当N0≤ 107次循环时, m1=3, lg
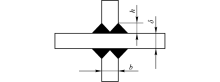
应力集中、板厚效应、残余应力及载荷比等因素影响焊接接头的疲劳行为[12], 在热点应力的求解时, 主板厚度效应尤为明显.对于角接接头的焊缝形式, 国际焊接学会规定:当焊接件主板厚度大于参考厚度时需要进行板厚修正, 其参考厚度一般为16 mm; 当主板厚度小于参考厚度时, 板厚效应不予考虑.在实际的工程分析中, 主板厚度较薄对焊接结构的疲劳强度也具有一定的影响, 为考察该类型板厚对其疲劳强度的影响, 从文献[13]中选取两组对比数据, 试件类型如图2所示.两组接头的载荷比R≈ 0, 焊趾角近似取为45° , 疲劳强度取循环寿命5× 106次的中值应力范围, 表1列出了相关参数及试验结果, 其中b和h分别为腹板厚度和焊趾高度.
| 表1 不同主板厚度的疲劳强度比较 Tab.1 Fatigue strength comparison of different motherboard thickness |
由表1可知, 焊接构件的主板厚度均小于标准中规定的参考厚度, 焊接件疲劳强度随着主板厚度的增加而明显减小, 因此当焊接构件的主板厚度小于参考厚度时, 需对基本S-N曲线进行板厚修正.依据国际焊接学会(IIW)中的建议[14], 厚度效应可通过式(6)对基本S-N曲线进行修正.
式中:Δ σ 为应力范围; N为应力范围Δ σ 作用下的循环次数; q为板厚修正系数; m为材料S-N曲线指数; tm为参考厚度.
考虑板厚效应时, FAT90S-N曲线作为热点应力S-N曲线的公式为
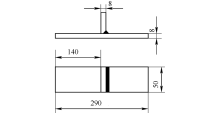
选用角接接头进行全焊透试件疲劳试验, 试件主板厚度为8 mm, 疲劳试件示意图如图3所示.试验在MTS810材料疲劳试验机上进行, 应力比R=-1, 加载频率为15 Hz.
应用成组法对焊接试件的疲劳性能进行测定, 应力水平σ max分别为130 MPa、140 MPa, 试件数为12, 其疲劳试验结果如表2所示.表2中平均值
式中:ε 为误差限度, 一般情况下取ε =5%; tr为概率密度函数; up为与可靠度相关的标准正态偏量;
| 表2 角接接头的疲劳试验结果 Tab.2 Fatigue test results of T-butt joint |
在试验结果中, 疲劳寿命数据具有一定的离散性, 分析其可能原因:试件材质本身的不均匀性, 试件加工质量及尺寸的差异及试验载荷存在一定的误差等因素.
在本试验研究中, 试验测试结果满足可靠度p=97.7%、置信度r=95%的安全疲劳寿命的要求, 则可依据式(11)计算可靠度p=97.7%的安全疲劳寿命, 计算结果见表3.
| 表3 角接接头的疲劳寿命 Tab.3 Fatigue life of T-butt joint 万次 |
疲劳试验采用名义应力法对角接接头进行疲劳寿命的评估, 需依据焊接接头对应的热点疲劳应力集中系数进行修正, 其公式为
式中:khs是热点疲劳应力集中系数; σ 是焊接试件所受的名义应力值.
根据文献[7]对焊接接头热点应力集中系数的有限元分析, 取khs=1.17.应用热点应力法对试件进行疲劳寿命计算并与试验法进行了对比分析, 其结果见表3.
由表3可以看出, 当主板厚度小于参考厚度且不考虑板厚效应(q=0)时, 计算结果偏于保守; 随着q值的增加, 计算值不断接近试验结果, q值过大(q=0.2)则使计算值偏于危险, 因此, 选取合理的板厚修正系数对焊接结构的寿命评估具有重要的影响.在本试验研究中, 取q=0.1时, 热点应力法计算出的疲劳寿命与试验获取试件的疲劳寿命具有很好的一致性, 从而验证了板厚效应修正后的热点应力S-N曲线用于焊接构件疲劳寿命评估时具有较高的精度和可靠性.
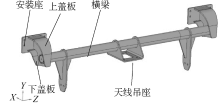
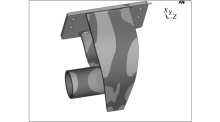
车辆天线梁安装在头车转向架上, 天线梁通过安装座螺栓与转向架构架侧梁端部连接, 横梁中部支座用于承载车载信号系统的天线装置, 其结构模型如图4所示.
该天线梁采用焊接结构, 其材料选用Q345E钢, 该材料基本力学性能如下:抗拉强度δ b为470~630 MPa; 屈服强度δ s为345 MPa; 弹性模量E为206 GPa; 泊松比μ 为0.3.
综合考虑整个天线梁的计算精度及两点线性外推确定焊趾处热点应力的要求, 选用20节点体单元Solid 186进行网格划分, 对关键焊缝进行模拟, 最终得到的有限元模型节点数为102 270, 单元数为68 629.另外, 考虑到天线装置对吊梁的作用力, 采用质心单元Mass21与梁单元Beam188进行模拟.焊接天线梁的有限元模型如图5所示.
1)静载荷.
静载荷是指车辆在停止状态下天线梁所承受的载荷, 主要由天线梁本身的质量、天线的质量等所产生的载荷组成.
2)动载荷.
动载荷是指车辆在运行状态下天线梁所承受的载荷.考虑到线路条件和车辆运行过程中的实际振动载荷, 取天线梁及其装置的垂向、纵向和横向加速度分别为10g, 7g和5g(g为重力加速度).
对模型施加3个方向的整体加速度, 在质心处施加由车载天线装置振动引起的外力, 在安装座处施加全约束.
1)平均应力.
由静载荷产生的应力为平均应力, 当结构受到脉动载荷作用时, 平均应力为静载荷应力与脉动载荷应力的1/2之和.
2)动应力幅值.
由动载荷产生应力为动应力幅值, 计算方法是各种动载荷计算应力的平方根.当受到脉动载荷作用时, 动应力幅值为动载荷应力与脉动载荷应力平方和的平方根[16], 其计算公式如下
式中:σ a为动应力幅值; σ 1, σ 2, …, σ n为各动载荷的计算应力.
图6给出了有限元分析局部应力云图, 整个焊接天线梁的疲劳薄弱部位为安装座座板与下盖板连接焊缝焊趾区, 这与天线梁线路运用中出现裂纹位置相吻合.
在复合应力状态下, 将有限元模型计算出的外推点的各向应力转化为垂直于焊缝方向的单向等效应力.表4和表5分别列出了0.5δ 和1.5δ 外推点在各个方向的动应力幅值和平均应力及通过式(5)计算出的单向等效应力.将表4、表5中的相关数据代入式(3)可得到安装座座板与下盖板连接焊缝焊趾处的等效热点应力值为120.5 MPa.将等效热点应力值代入式(7), 可得到焊接天线梁的疲劳寿命为7.1× 105次.对于无限寿命设计来讲, 焊接构件需满足疲劳寿命N=2× 106次, 即该天线梁的疲劳寿命不能满足使用要求, 需进行结构优化.
| 表4 外推点在各方向的应力幅值及等效应力 Tab.4 Stress amplitude and equivalent stress of extrapolation points MPa |
| 表5 外推点在各方向的平均应力值及等效应力 Tab.5 Mean stress and equivalent stress of extrapolation points MPa |
可见, 热点应力法结合有限元分析技术对焊缝焊趾处的疲劳分析具有很强的适应性, 板厚修正后的S-N曲线对焊接结构的疲劳寿命评估具有较高的可靠度和准确度.但热点应力法也具有局限性, 对于起始于焊根、内部焊接缺陷等部位的疲劳开裂情况有待进一步研究.
1)热点应力法应用于焊接结构的疲劳分析时, 需考虑结构件的主板厚度效应, 试验分析表明:修正后的FAT90作为一条热点应力S-N曲线在焊接构件疲劳寿命评估时具有较高的精度和可靠性.
2)运用ANSYS程序对运营状态下的车辆天线梁进行了有限元分析, 结果表明: 其最大应力发生在安装座座板与下盖板连接焊缝焊趾区, 这与天线梁线路运用中出现裂纹位置相吻合.
3)以热点应力作为控制参量, 应用修正热点应力S-N曲线对焊接天线梁进行了疲劳寿命计算, 其疲劳寿命为7.1× 105次, 不能满足使用要求, 需进行结构优化设计.
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|