基于时空特征的城市轨道交通客流量预测方法

引用本文

袁坚, 王鹏, 王钺, 杨欣. 基于时空特征的城市轨道交通客流量预测方法[J]. 北京交通大学学报, 2017,41(6): 42-48.
YUAN Jian, WANG Peng, WANG Yue, YANG Xin. A passenger volume prediction method based on temporal and spatial characteristics for urban rail transit[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2017,41(6): 42-48.
Doi:10.11860/j.issn.1673-0291.2017.06.007 复制到剪切板

Permissions

北京交通大学学报编辑部所有

基于时空特征的城市轨道交通客流量预测方法

袁坚¹, 王鹏¹, 王钺¹, 杨欣²

1.清华大学电子工程系,北京 100084

2.北京交通大学轨道交通控制与安全国家重点实验室,北京 100044

第一作者:袁坚(1965—),男,江苏东台人,教授,博士. 研究方向为信息与网络安全、网络移动性、动力学复杂性和认知网络等.email:jyuan@tsinghua.edu.cn.

收稿日期: 2017-03-30

基金: 国家自然科学基金(71701013,61673237,71621001, 71525002)

摘要

随着城市轨道交通网络运营里程的不断增长及网络承载客流量的不断提高,特定站点客流量极易发生急剧变化,这种变化引起整个网络客流量的不均匀分布,从而增加运营调度的难度和运营事故的发生概率.本文以城市轨道交通实际运营中采集的大量客流数据为基础,从时间和空间两个维度分析城市轨道交通客流分布的特点,并进一步提出基于贝叶斯网络的客流量预测方法,实现对特定站点的客流量预测.本实验完全基于实际数据,结果表明:预测客流量平均绝对百分比误差基本在0.1以下,预测准确程度较高.

关键词: 城市轨道交通; 客流预测; 贝叶斯网络; 时空特征

中图分类号:U293.6 文献标志码:A 文章编号:1673-0291(2017)06-0042-07

A passenger volume prediction method based on temporal and spatial characteristics for urban rail transit

YUAN Jian¹, WANG Peng¹, WANG Yue¹, YANG Xin²

1.Department of Electronic Engineering Tsinghua University, Beijing 100084,China

2.State Key Lab of Rail Traffic Control & Safety, Beijing Jiaotong University, Beijing 100044,China;

Fund:National Natural Science Foundation of China(71701013,61673237,71621001, 71525002)

Abstract

With the expanding of urban rail transit network revenue length and the increasing of its passenger volume, the passenger volume for some subway stations is susceptible to rapid changes, which can easily incur uneven distribution of the entire network traffic. It could therefore increase the difficulty of rail transit operations and probability of operational incidents. On the basis of passenger volume data collected from practical operation, this paper analyzes the temporal and spatial characteristics of the passenger volume. It also proposes a passenger volume prediction method using the Bayesian network to predict the passenger volume of certain subway stations. Based on practical data, these numerical experiments demonstrate that the proposed method can achieve an mean absolute percentage error below 0.1 when predicting, proving the model is highly accurate.

Keyword: urban rail transit; passenger volume prediction; Bayesian network; temporal and spatial characteristics

文章图片

城市轨道交通是城市公共交通系统的重要组成部分, 是城市交通的主动脉.随着城市轨道交通网络日趋复杂和日均客流量屡创新高, 轨道交通网络单点客流量极易突变, 单条线路甚至路网的短时瘫痪可能性大大提高, 进而增加轨道交通路网运营的各类潜在风险^[1].充分利用城市轨道交通实际运营数据, 掌握特定站点客流量分布的时空规律^{[2, 3, 4, 5]}, 能够降低预测客流量的平均绝对百分比误差, 从而提高客流量预测准确程度, 对疏导客流和合理配置运营资源具有重要意义.

目前, 城市轨道交通客流量的规律分析和预测方法已经成为近年来的研究热点.文献[6]通过出行总量预测、小区OD出行预测、进出站流量预测和交通网流量分配4个阶段分析, 建立了客流预测分析模型.文献[7]建立了面向“ 区域+市区” 的多层次多模式客流预测方法, 提出了权重分配法、类重力模型法和目的地选择模型法.文献[8]利用实际客流数据, 针对北京城市轨道交通的特有特征深入分析研究了BP神经网络用于客流预测的实用性和合理性.文献[9]通过聚类分析, 建立了基于改进BP神经网络的轨道交通短时客流预测模型.上述研究着重从单个因素建模预测轨道交通客流量, 然而从实际轨道交通运营数据来看, 轨道交通客流量往往受多个因素同时影响^{[10, 11]}.

本文作者以城市轨道交通自动售检票系统采集的实际客流数据为基础, 将城市轨道交通中的车站分普通站和换乘站, 分析客流分布的时间和空间特征; 借助贝叶斯网络(Bayesian Networks, BN)方法, 按工作日和非工作日分类, 对影响客流量的历史信息、邻站信息等因素进行贝叶斯网络建模, 实现特定车站、特定时间轨道交通车站进和出站客流量预测.

1 客流数据

1.1 数据来源

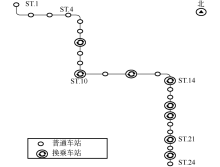
客流数据来源于北京轨道交通某线路自动售检票系统采集的实际客流信息, 包含24个车站、24个月(2013-07-01— 2015-06-30)进站和出站客流量.系统每隔30 min采集数据样本, 即每当整点和半点时刻完成一次数据的收集、汇总和存储.该线路每天地铁运营约19.5 h(运营时间为4:40-23:38), 合计每天采样39段.该线路共有普通车站(非换乘车站)16座、换乘车站8座, 按由北至南顺序对车站简化命名为ST.1至ST.24, 线路具体情况如图1所示.

	Figure Option View Download New Window
	图1 北京轨道交通某线路车站类型示意图Fig.1 Schematic diagram of a typical station in Beijing rail transit

收集本线路24个车站的进站、出站客流量生成两组数据, 每组数据的时间跨度均为730 d, 形成矩阵为730× 39行、24列的轨道交通客流矩阵C.

1.2 客流时间分布

1.2.1 时间分布基本特征

在获得的轨道交通客流数据矩阵中, ST.4相邻车站无换乘情况, 附近无交通枢纽或商业中心等明显引起客流剧增的情况, 为典型的普通车站; 车站ST.21与另一条地铁、火车站换乘, 为交通枢纽换乘车站, 故选取此两站作为典型车站.下文中均以此两站为例, 随机选取一周时间(2015-06-22— 2015-06-28)说明轨道交通客流时间特征(见图1).

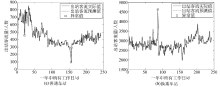
1)从时间维度上看, 工作日轨道交通客流早晚高峰特征明显.从图2可以看出, 在工作日早7:00-9:00、晚5:00-7:00出现客流高峰, 普通车站和换乘车站早、晚高峰客流量峰值远远大于平峰时段平均客流量, 换乘车站在周一早高峰、周五晚高峰出现明显大客流现象.

	Figure Option View Download New Window
	图2 普通车站和换乘车站一周客流情况Fig.2 Weekly passenger flow situation of ordinary & transfer station

2)工作日和非工作日的客流趋势差异显著.以普通车站ST.4为例, 非工作日客流总量比工作日客流总量有所降低, 减少约29.2%; 而换乘车站ST.21非工作日客流总量较工作日客流总量有所增加, 增加约26.7%.非工作日则无明显客流早晚高峰现象, 但出行时间相对集中, 一般在10:00-14:00期间达到客流峰值.工作日和非工作日的高峰客流变化表明不同时间段人们出行规律不同.

1.2.2 相邻时间段客流特征

1)客流在时间尺度上具有稳定性, 同一时段历史客流数值相近.以一年(2014-07— 2015-06)所有工作日的8:30-9:00为例计算客流稳定程度, 并以标准差系数来反映变动程度, 标准差系数越小说明客流变化程度越小, 见表1.

表1 普通车站和换乘车站客流时间尺度特征 Tab.1 Time scale characteristics of passenger flow at ordinary & transfer station

车站编号	进站客流			出站客流
车站编号	$\overset{̅}{x}$ /人数	σ	V	$\overset{̅}{x}$ /人数	σ	V
普通车站ST.4	593	98.6	0.166	452	134.5	0.297
换乘车站ST.21	2 352	301.9	0.128	2 847	308.6	0.108

表1 普通车站和换乘车站客流时间尺度特征 Tab.1 Time scale characteristics of passenger flow at ordinary & transfer station

标准差系数V计算方法:V=σ / $\overset{̅}{x}$ × 100%, 其中 $\overset{̅}{x}$ 表示此段时间内客流平均值; σ 表示此段时间内客流标准差.

上述数据的标准差系数说明工作日同一时段客流量波动不大, 因此, 客流的历史数值相关性可以作为客流预测的因素之一.

2)相邻时段客流量具有相关性, 分别以普通车站(ST.4)和换乘车站(ST.21)为例, 对比一年所有工作日中8:00-8:30、8:30-9:00、9:00-9:30共3个时间段的进、出站客流量相邻时段差值的累计分布函数(Cumulative Distribution Function, CDF)曲线, 如图3所示, 结果表明:同一站点相邻时间段进站、出站客流量变化趋势基本相近, 在客流时间特征上具有相关性, 仅在客流量级上有所差异; 在后续预测中, 本实验对客流量进行量化分级.由于客流变化趋势具有相关性, 量化后各级之间变化也具有相关性, 故相邻时间段客流量相关性是客流预测的一项重要因素.

	Figure Option View Download New Window
	图3 进出站客流相邻时段客流差值CDF曲线Fig.3 CDF curve of inbound & outbound passenger flow between adjacent time interval

1.3 客流空间分布

1.3.1 空间分布基本特征

由于线路各车站周边用地类型不同, 如交通枢纽、商业区、景区和高校等, 轨道交通客流在空间分布上存在显著的不均衡性, 普通车站和换乘车站客流量有巨大差异性.根据获得的轨道交通客流数据矩阵, 以典型的轨道交通地铁车站(普通车站、换乘车站)的特定时间(2015-06-22— 2015-06-28)为例, 分析轨道交通客流空间特征如图2所示.

从图2中可以看出, 换乘车站ST.21平均进、出站客流量约是普通车站ST.4的4倍; 从客流变化趋势上看, 普通车站和换乘车站的趋势相近, 两车站均出现早晚高峰客流剧增现象.

1.3.2 相邻车站客流特征

相邻车站空间距离相近, 故其客流量存在相关性.分别以普通车站(ST.4)和换乘车站(ST.21)为例, 对比一年(2014-07— 2015-06)所有工作日的8:30-9:00时段进、出站客流量相邻车站差值的CDF曲线.如图4所示, 可以发现相邻车站客流量的变化趋势相近.因此, 客流量在空间特征上具有的相关性, 仅在客流量级上有所差异, 故相邻车站的客流量空间相关性也可以作为客流预测的因素之一.

	Figure Option View Download New Window
	图4 进出站客流相邻车站客流差值CDF曲线Fig.4 CDF curves of inbound & outbound passenger flow difference between adjacent stations

2 贝叶斯网络预测模型

2.1 贝叶斯网络预测模型建立

预测模型根据轨道交通中地铁客流时空特征, 将客流量分成不同等级, 采用贝叶斯网络(Bayesian Networks, BN)方法, 综合考虑客流量时间相关性、客流量空间相关性、客流量历史数据相关性等因素, 通过实际数据实现特定站点的进、出站的客流预测.

根据贝叶斯网络理论, 建立客流预测模型^{[12, 13]}, 如图5所示.

	Figure Option View Download New Window
	图5 基于贝叶斯网络的客流预测模型Fig.5 Passenger flow forecast model based on Bayesian network

1)从客流矩阵C中提取相关的客流时间数据Q¹、客流空间数据Q²和客流历史数据Q³.以Q(t, s)表示站点s在第t个时间点客流量, Q(t-T, s)表示本站点在第t个时间点历史同时段客流量, T表示每天时段总数.结合1.2节、1.3节中结论, 带预测客流量状态Q(t, s)(简化为Q^P)受时间数据Q(t-1, s)(简化为Q^T)、客流空间数据Q(t-1, s-1)(简化为Q^S)和历史客流数据Q(t-1, s)(简化为Q^H)的综合影响.

2)选取待预测客流量Q^P, 参考交通状态推算模型^[12], 并结合实际轨道交通客流特征与城市道路交通规划设计规范, 对相关客流数据Q^T、Q^S、Q^H进行量化分级, 分为n级, 每一级记为i(i=1, …, n), 计算各组数据每个客流等级概率P $({Q^{T}}_{i})$ 、P $({Q^{S}}_{i})$ 、P $({Q^{H}}_{i})$ .

3)依据每个客流等级概率P $({Q^{T}}_{i})$ 、P $({Q^{S}}_{i})$ 、P $({Q^{H}}_{i})$ 推算待预测各客流等级的概率P( ${Q^{P}}_{i}$ ), 贝叶斯网络公式为

$\begin{array}{l} P ({Q^{P}}_{i} |{Q^{T}}_{i} ⋂ {Q^{S}}_{i} ⋂ {Q^{H}}_{i}) = \\ \frac{P ({Q^{T}}_{i} |{Q^{P}}_{i}) P ({Q^{S}}_{i} |{Q^{P}}_{i}) P ({Q^{H}}_{i} |{Q^{P}}_{i})}{\overset{n}{\sum_{j = 1}} P ({Q^{T}}_{j} ⋂ {Q^{S}}_{j} ⋂ {Q^{H}}_{j}) P ({Q^{P}}_{j})} (1) \end{array}$

假设时间数据 ${Q^{T}}_{i}$ 、空间数据 ${Q^{S}}_{i}$ 和客流历史数据 ${Q^{H}}_{i}$ 相互独立, 有

$\begin{array}{l} P ({Q^{P}}_{i} |{Q^{T}}_{i} ⋂ {Q^{S}}_{i} ⋂ {Q^{H}}_{i}) = \\ P ({Q^{H}}_{i} |{Q^{P}}_{i}) P ({Q^{S}}_{i} |{Q^{P}}_{i}) P ({Q^{H}}_{i} |{Q^{P}}_{i}) (2) \end{array}$

将式(2)代入式(1)中, 式(1)可简化为

$\begin{array}{l} P ({Q^{P}}_{i} |{Q^{T}}_{i} ⋂ {Q^{S}}_{i} ⋂ {Q^{H}}_{i}) = \\ \frac{P ({Q^{T}}_{i} |{Q^{P}}_{i}) P ({Q^{S}}_{i} |{Q^{P}}_{i}) P ({Q^{H}}_{i} |{Q^{P}}_{i})}{\overset{n}{\sum_{j = 1}} P ({Q^{T}}_{j} |{Q^{P}}_{j}) P ({Q^{S}}_{j} |{Q^{P}}_{j}) P ({Q^{H}}_{j} |{Q^{P}}_{j}) P ({Q^{P}}_{j})} (3) \end{array}$

4)分别计算P( ${Q^{T}}_{i} |{Q^{P}}_{i}$ )、P( ${Q^{S}}_{i} |{Q^{P}}_{i}$ )、P( ${Q^{H}}_{i} |{Q^{P}}_{i}$ ), 并结合各客流等级对应的客流均值, 完成轨道交通客流量Q^P的预测.

2.2 贝叶斯网络预测模型求解

采样时间序列数据、空间数据和历史时段客流数据, 基于贝叶斯网络客流量预测模型, 总结先验知识, 实现对特定车站s、特定时段t客流量状态的预测, 最终得到客流量预测值.

1)根据2.1节模型, 选择预测时间段、空间、训练序列长度.①时间段选择:选取典型预测时段为工作日的早高峰时段(选取时段为8:30-9:00).②空间选择:典型车站选择普通车站ST.4和换乘车站ST.21.③训练序列长度L选择:训练序列长度可变, 通过数据训练得出, L取22 d时预测效果最优.最后, 通过一定时间段验证模型预测效果, 验证时间段设置为244 d.

2)通过已采集的客流量数据C, 根据步骤1)中的设置, 生成可用进、出站客流量矩阵C₁、C₂.

3)对客流量矩阵C₁、C₂进行量化分级, 分为n级, 每一级记为i(i=1, …, n), 计算客流量化等级基础值Q_step, 公式为

$Q_{step} = (Q_{\max} - Q_{\min}) / n (4)$

经验证将客流状态划分平均为6个等级最为合理, 即n=6.

4)计算各进、出站客流等级i的客流均值Q_{i_}_ong和对应的概率分布P( ${Q^{P}}_{i}$ ).

5)计算客流量等级i时间数据 ${Q^{T}}_{i}$ 概率分布P( ${Q^{T}}_{i}$ ); 客流量等级i空间数据 ${Q^{S}}_{i}$ 概率分布P( ${Q^{S}}_{i}$ ); 客流量等级i历史时刻数据 ${Q^{H}}_{i}$ 概率分布P( ${Q^{H}}_{i}$ ).

6)根据式(3)和步骤4)、5)得出的数据P( ${Q^{P}}_{i}$ )、P( ${Q^{T}}_{i}$ )、P( ${Q^{S}}_{i}$ )、P( ${Q^{H}}_{i}$ ), 计算预测各客流量等级P( ${Q^{P}}_{i} |{Q^{T}}_{i} ⋂ {Q^{S}}_{i}$ ∩ ${Q^{H}}_{i}$ ).

7)结合步骤4)Q_{i_}_ong和步骤6)P( ${Q^{P}}_{i} |{Q^{T}}_{i} ⋂ {Q^{S}}_{i}$ ∩ ${Q^{H}}_{i}$ ), 计算预测客流值Q_prediction, 公式为

$Q_{prediction} = \overset{n}{\sum_{i = 1}} Q_{i_ong} \times P ({Q^{P}}_{i} |{Q^{T}}_{i} ⋂ {Q^{S}}_{i} ⋂ {Q^{H}}_{i}) (5)$

3 贝叶斯网络预测分析

3.1 进站客流量预测结果分析

1)选取客流数据中一年时间工作日早高峰时段(8:30-9:00), 对普通车站ST.4和换乘车站ST.21进站客流量贝叶斯网络预测, 结果如图7所示, 表明进站客流预测值与实际值符合程度较高.

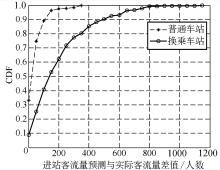	Figure Option View Download New Window
	图7 进站客流预测值与实际值的差值CDF曲线Fig.7 CDF curves of the difference between predicted value and the actual value of inbound passenger flow

客流量预测方法有一定的异常检测能力, 本预测算法通过大量数据, 综合历史数据相关性、相邻时间段和相邻车站相关性进行预测.如果实际客流量数据明显与预测客流量数据存在较大差异(排除已知的客流异动状态), 这种较大差异性可作为异常检测的判断依据.如图6所示, 普通车站客流量曲线中有7个异常点, 换乘车站客流量曲线有4个异常点.

	Figure Option View Download New Window
	图6 普通车站和换乘车站进站客流预测情况Fig.6 Inbound passenger flow forecast of ordinary & transfer station

2)以进站客流量预测值与实际值之差做CDF曲线, 如图7所示, 普通车站预测值与实际值相对误差的绝对值小于100(此段客流均值为593)的点占比在90% 以上, 换乘车站预测值与实际值相对误差的绝对值小于500(此段客流均值为2 352)的点占比在90% 以上.

平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)是一种统计学上对预测精度的度量方法.定义Δ _MAPE= $\frac{100}{n} \overset{n}{\sum_{i = 1}} |\frac{A_{i} - F_{i}}{A_{i}}|$ , 其中:A_i为实际值; F_i为预测值; n为总预测个数.计算预测进站客流平均绝对百分比误差, 可得普通车站Δ _MAPE=0.097 0, 换乘车站Δ _MAPE=0.083 1, 说明模型预测性能良好.

3.2 出站客流量预测结果分析

1)选取客流数据中一年时间工作日早高峰时段(8:30-9:00), 对普通车站ST.4和换乘车站ST.21出站客流量进行贝叶斯网络预测, 结果如图8所示.

	Figure Option View Download New Window
	图8 普通车站和换乘车站出站客流预测情况Fig.8 Outbound passenger flow forecast of ordinary & transfer station

客流量预测值与实际值符合程度较高.同进站客流预测情况类似, 出站客流预测方法也具有一定的异常检测能力, 如图8所示, 普通车站客流量曲线中有5个异常点, 换乘车站客流量曲线有3个异常点.

2)以出站客流量预测值与实际值之差做CDF曲线, 如图9所示.

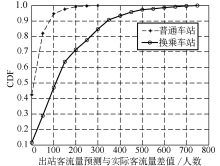	Figure Option View Download New Window
	图9 出站客流预测值与实际值的差值CDF曲线Fig.9 CDF curves of the difference between predicted value and the actual value of outbound passenger flow

普通车站预测值与实际值相对误差的绝对值小于90(此段客流均值是452)的点占比在90% 以上, 换乘车站预测值与实际值相对误差的绝对值小于350(此段客流均值是2 847)的点占比在90% 以上.计算预测出站客流平均绝对百分比误差, 普通车站Δ _MAPE=0.103 4, 换乘车站Δ _MAPE=0.060 0, 说明模型预测性能良好.

4 结论

本文作者对城市轨道交通进、出站客流量的预测方法进行了研究, 阐述了客流量时、空特点并进行深入分析, 借助贝叶斯网络方法, 结合客流分布的相邻时间、相邻空间、历史时段数据等相关性特征, 建立贝叶斯网络客流量预测模型, 并通过大量实际数据分析, 对特定车站、特定时间客流量进行预测; 结果显示客流Δ _MAPE大多小于0.1, 可以满足轨道交通运营和调度要求, 同时本模型具有的异常检测能力, 进一步加强了本模型的实用性.

本文的贝叶斯网络客流预测模型可以实现后台快速实时计算, 为城市轨道交通人流密度预警、客流引导和运营调度提供重要数据依据.

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	北京交通发展研究中心. 2015年交通运行报告[R]. 北京: 北京交通发展研究中心, 2015. Beijing Traffic Development Research Center. 2015 traffic report[R]. Beijing: Beijing Traffic Development Research Center, 2015. (in Chinese) [本文引用:1]
[2]	四兵锋, 何九冉, 任华玲, 等. 基于时序特征的城市轨道交通客流预测[J]. 北京交通大学学报, 2014, 38(3): 1-6. SI Bingfeng, HE Jiuran, REN Hualing, et al. Urban railway traffic passenger flow forecast based on the timing characteristics[J]. Journal of Beijing Jiaotong University, 2014, 38(3): 1-6. (in Chinese) [本文引用:1]
[3]	王静, 刘剑锋, 马毅林, 等. 北京市轨道交通车站客流时空分布特征[J]. 城市交通, 2013, 11(6): 18-27. WANG Jing, LIU Jianfeng, MA Yilin, et al. Temporal and spatial passenger flow distribution characteristics at rail transit stations in Beijing[J]. Urban Transport of China, 2013, 11(6): 18-27. (in Chinese) [本文引用:1]
[4]	张成. 城市轨道交通客流特征分析[D]. 成都: 西南交通大学, 2006. ZHANG Cheng. Analysis on the characteristics of urban rail transit passenger flow[D]. Chengdu: Southwest Jiaotong University, 2006. (in Chinese) [本文引用:1]
[5]	段卫静, 陈艳艳, 赖见辉. 北京地铁4号线客流特征分析[J]. 都市快轨交通, 2013, 26(4): 43-46. DUAN Weijing, CHEN Yanyan, LAI Jianhui. Passenger flow characteristics in Beijing subway line 4[J]. Urban Rapid Rail Transit, 2013, 26(4): 43-46. (in Chinese) . [本文引用:1]
[6]	康海燕. 北京轨道交通客流预测模型的研究[J]. 铁道运输与经济, 2002, 24(12): 21-23. KANG Haiyan. Studying the passenger volume forecast for Beijing urban track traffic[J]. Railway Transport and Economy, 2002, 24(12): 21-23. (in Chinese) [本文引用:1]
[7]	王玉萍. 城市轨道交通客流预测与分析方法[D]. 西安: 长安大学, 2011. WANG Yuping. Study on urban rail transit passenger forecast and analysis[D]. Xi'an: Chang'an University, 2011. (in Chinese) [本文引用:1]
[8]	王丽娜. 基于历史客流数据的城市轨道交通网络客流量预测及调度研究[D]. 北京: 北京交通大学, 2011. WANG Lina. Traffic forecasting and scheduling of the urban passenger rail network based on historical data[D]. Beijing: Beijing Jiaotong University, 2011. (in Chinese) [本文引用:1]
[9]	董升伟. 基于改进BP神经网络的轨道交通短时客流预测方法研究[D]. 北京: 北京交通大学, 2013. DONG Shengwei. The research of short-time passenger flow forecasting based on improved BP neural network in urban rail transit[D]. Beijing: Beijing Jiaotong University, 2013. (in Chinese) [本文引用:1]
[10]	陈伯阳, 蒋明清, 四兵锋, 等. 基于乘客个体属性的地铁客流分配算法及实证研究[J]. 北京交通大学学报, 2015, 39(6): 39-47. CHEN Boyang, JIANG Mingqing, SI Bingfeng, et al. Individual attributes based assignment model and empirical research for urban subway network[J]. Journal of Beijing Jiaotong University, 2015, 39(6): 39-47. (in Chinese) [本文引用:1]
[11]	蔡昌俊, 姚恩建, 王梅英, 等. 基于乘积ARIMA模型的城市轨道交通进出站客流量预测[J]. 北京交通大学学报, 2014, 38(2): 135-140. CAI Changjun, YAO Enjian, WANG Meiying, et al. Prediction of urban railway stations entrance and exit passenger flow based on multiply ARIMA model[J]. Journal of Beijing Jiaotong University, 2014, 38(2): 135-140. (in Chinese) [本文引用:1]
[12]	陆化普, 孙智源, 屈闻聪. 基于动态阈值的交通流故障数据实时识别方法[J]. 土木工程学报, 2015, 48(11): 126-132. LU Huapu, SUN Zhiyuan, QU Wencong. Real-time identification of traffic erroneous data based on dynamic threshold[J]. China Civil Engineering Journal, 2015, 48(11): 126-132. (in Chinese) [本文引用:2]
[13]	徐薇, 黄厚宽, 秦勇. 基于时空数据挖掘的铁路客流预测方法[J]. 北京交通大学学报, 2004, 28(5): 16-19. XU Wei, HUAN Houkuan, QIN Yong. Study of railway passenger flow forecasting method based on spatio-temporal data mining[J]. Journal of Beijing Jiaotong University, 2004, 28(5): 16-19. (in Chinese) [本文引用:1]

2015

0.0

... 随着城市轨道交通网络日趋复杂和日均客流量屡创新高,轨道交通网络单点客流量极易突变,单条线路甚至路网的短时瘫痪可能性大大提高,进而增加轨道交通路网运营的各类潜在风险^[1] ...

2014

0.0

... 充分利用城市轨道交通实际运营数据,掌握特定站点客流量分布的时空规律^[2,3,4,5],能够降低预测客流量的平均绝对百分比误差,从而提高客流量预测准确程度,对疏导客流和合理配置运营资源具有重要意义 ...

2013

0.0

2006

0.0

2013

0.0

2002

0.0

... 文献[6]通过出行总量预测、小区OD出行预测、进出站流量预测和交通网流量分配4个阶段分析,建立了客流预测分析模型 ...

2011

0.0

... 文献[7]建立了面向#cod#x0201c ...

2011

0.0

... 文献[8]利用实际客流数据,针对北京城市轨道交通的特有特征深入分析研究了BP神经网络用于客流预测的实用性和合理性 ...

2013

0.0

... 文献[9]通过聚类分析,建立了基于改进BP神经网络的轨道交通短时客流预测模型 ...

2015

0.0

... 上述研究着重从单个因素建模预测轨道交通客流量,然而从实际轨道交通运营数据来看,轨道交通客流量往往受多个因素同时影响^[10,11] ...

2014

0.0

... 上述研究着重从单个因素建模预测轨道交通客流量,然而从实际轨道交通运营数据来看,轨道交通客流量往往受多个因素同时影响^[10,11] ...

2015

0.0

... 根据贝叶斯网络理论,建立客流预测模型^[12,13],如图5所示 ...

... 2)选取待预测客流量Q^P,参考交通状态推算模型^[12],并结合实际轨道交通客流特征与城市道路交通规划设计规范,对相关客流数据Q^T、Q^S、Q^H进行量化分级,分为n级,每一级记为i(i=1,…,n),计算各组数据每个客流等级概率PQTi、PQSi、PQHi ...

2004

0.0

... 根据贝叶斯网络理论,建立客流预测模型^[12,13],如图5所示 ...