引用本文
周航, 韩权. 具有去除椒盐噪声能力的改进双边滤波算法[J]. 北京交通大学学报, 2017,41(5): 43-51.
ZHOU Hang, HAN Quan. An improved bilateral filtering algorithm having the ability to remove salt-and-pepper noise[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2017,41(5): 43-51.
Doi:10.11860/j.issn.1673-0291.2017.05.007  
Permissions
Copyright©2017, 北京交通大学学报编辑部
北京交通大学学报编辑部 所有
具有去除椒盐噪声能力的改进双边滤波算法
周航, 韩权
北京交通大学 电子信息工程学院,北京 100044

第一作者:周航(1974—),男,四川成都人,副教授.研究方向为计算机视觉和信号处理.email:hangzhou@bjtu.edu.cn

收稿日期: 2017-03-06
基金: 国家自然科学基金项目(61573057)
摘要

针对双边滤波器不能有效去除椒盐噪声这一特点,本文提出了一种自适应大小的模板替换算法,通过先替换双边滤波模板区域像素值,再对替换后的模板区域做双边滤波,使其在具有双边滤波保边并去除低频噪声能力的基础上兼具去除椒盐噪声的能力.实验结果证明:本文提出的算法在双边滤波的基础上可以有效去除图像中的椒盐噪声,与几种经典去除椒盐噪声的算法相比,在噪声密度10%~90%的情况下,峰值信噪比(PSNR)平均值提升5.8%以上,结构相似性(SSIM)平均值提升2.75%以上.

关键词: 图像处理; 双边滤波; 模板替换; 椒盐噪声
中图分类号:TP391
An improved bilateral filtering algorithm having the ability to remove salt-and-pepper noise
ZHOU Hang, HAN Quan
School of Electronic and Information Engineering, Beijing Jiaotong University, Beijing 100044,China
Fund:Foundation item:National Natural Science Foundation of China (61573057)
Abstract

In allusion to the feature of bilateral filter having not the ability to remove salt-and-pepper noise, this paper proposes a adaptive template replacement algorithm, which firstly replaces the pixel value of bilateral filtering template areas and then bilateral filtering can be made for the replaced template areas to have the ability to remove the salt-and-pepper noise when equipped with the capacity of removing low-frequency noise while remaining edge with bilateral filtering. The experimental results show that improved bilateral filtering algorithm can remove salt-and-pepper noise well, and compared with several classical algorithms having the ability to remove salt-and-pepper noise, the average value of PSNR calculated by the proposed algorithm has been improved more than 5.8% and the average value of SSIM has been enhanced more than 2.75% under the condition of 10%~90% of noise density.

Keyword: image processing; bilateral filtering; template replacement; salt-and-pepper noise

在图像的采集、传输和处理过程中, 图像受环境、器材及处理方法的影响, 不可避免的会产生不同程度的噪声, 其中高斯噪声和椒盐噪声是较为常见的图像噪声污染源.受噪声影响, 往往会给后续的图像处理(如识别和分割等)带来较大的影响, 因此有效去除图像中的各种噪声显得尤为必要.

针对高斯噪声, 高斯滤波是一种简单可行的噪声处理方法, 但高斯滤波在去除高斯噪声的同时会使图像丢失边缘等细节信息, 从而使图像变得模糊, 降低图像的整体质量.文献[1]提出了著名的双边滤波(Bilateral filter)算法, 在高斯滤波器的基础上考虑像素间灰度值的差别, 在去噪的同时可以保持图像边缘的清晰.但由于双边滤波采用高斯核作为算法基础来对带有噪声的图像进行处理, 因此并不具备去除椒盐噪声的能力.

针对椒盐噪声, 标准中值滤波(SMF)算法[2]是一种简单有效的噪声处理方法, 但当椒盐噪声密度较高时, 中值滤波的滤波效果很差, 且中值滤波模板区域越大, 图像边缘会变得越模糊.针对中值滤波的这些缺点, 近年来有研究人员提出新的算法来获得更好地去噪效果, 其中较为经典的算法有:文献[3]提出的自适应中值加权滤波(Adaptive Center Weighted Median Filter, ACWMF)算法.文献[4]提出的递进开关中值滤波(Progressive Switching Median Filter, PSMF)算法.文献[5]提出的基于决策(Decision-Based Algorithm, DBA)算法.文献[6]提出的模糊自适应中值(Noise Adaptive Fuzzy Switching Median Filter, NAFSMF)算法.文献[7, 8]提出的改进的基于决策的不对称裁剪的中值滤波(Modified Decision-Based Unsymmetrical Trimmed Median Filter, MDBUTMF)算法.文献[9]提出的弹性中值滤波1(Elastic Median Filter1 , EMF1)算法, 弹性中值滤波2(Elastic Median Filter 2, EMF2)算法.

但以上改进算法均在高密度椒盐噪声下性能快速下降, 为此本文作者提出了一种先替换双边滤波器模板区域像素值, 再用替换后的模板区域进行双边滤波的方法来改进双边滤波算法, 从而在双边滤波基础上对高密度椒盐噪声进行有效滤波.用DBA、NAFSMF、MDBUTMF、EMF1、EMF2算法与本文改进算法的椒盐噪声去除能力进行了对比, 采用了峰值信噪比(PSNR)和结构相似性(SSIM)作为图像质量客观评价标准.实验结果证明本文提出的算法在椒盐噪声的去除能力上优于5种算法.

1 NAFSMF和MDBUTMF算法分析
1.1 NAFSMF算法

NAFSMF算法在椒盐噪声点将当前像素值和所在邻域的中值进行加权平均后再进行赋值, 其邻域所用模板大小不固定, 弥补了中值滤波算法限定模板大小的不足.算法设定两个阈值 T1和T2, T1=10, T2=30, 以3× 3作为最小模板大小设置自适应模板检测模板中心点附近像素点的灰度值, 直到检测到非椒盐噪声点为止, 此时的模板大小记为w× w, w的最大值为7.

设模板中心点像素灰度值为 P(i, j), 记 M(i, j)=median(Pi-w, j-w, Pi, j-w, Pi+w, j-w, Pi-w, j), 记 D(i, j)为该点附近3× 3的模板区域内其他像素灰度值与 P(i, j)差值的最大值.根据 D(i, j)的大小做如下判断, 记 F(i, j)为

Fi, j=0, Di, j< T11, Di, j> T2(Di, j-T1)/(T2-T1), 其他情况(1)

将模板中心像素点的灰度值 P(i, j)替换为 1-F(i, j)×P(i, j)+F(i, j)×M(i, j).

NAFSMF算法极大地改善了FSMF算法的性能[10], 在处理高密度椒盐噪声图像时性能优良, 处理中低密度椒盐噪声图像时性能相对较差.实验表明, 当椒盐噪声密度高于80%时NAFSMF算法性能快速下降但滤波效果仍然显著.

1.2 MDBUTMF算法

针对高密度椒盐噪声污染的图像, MDBUTMF在基于决策的非对称裁剪中值滤波器(DBUTMF)[11]的基础上增加了噪声检测机制.MDBUTMF算法固定使用3× 3的模板窗口.

如果模板中心像素点是椒盐噪声点, 则对该点进行滤波.对椒盐噪声点进行滤波时, 如果模板内所有点均为椒盐噪声点, 则使用模板中所有点灰度值的均值来替换 P(i, j); 如果模板中有非椒盐噪声点存在, 则移除椒盐噪声点后用剩余像素点灰度值的中值替换 P(i, j).由于该算法采用固定大小模板滤波, 利用均值代替中心像素, 因此算法鲁棒性较低, 对部分图像滤波无效.

MDBUTMF算法在处理低密度椒盐噪声图像时性能优良, 在处理中高密度椒盐噪声时性能快速下降.其主要原因在于当图像中椒盐噪声密度较高时, 3× 3的模板区域内所有点均为椒盐噪声点的概率变大, 其灰度值的均值与中心点的真实灰度值相差较大, 因此算法性能快速下降.

2 改进算法及自适应模板替换
2.1 双边滤波的算法改进

双边滤波是一种以高斯核(Gaussian Kernel)为基础的非线性的滤波方法, 可以同时考虑像素的空间距离和像素间灰度值的差别, 从而达到保边去噪的目的.其基本公式为

BF[I]p=1Wp∑q∈SGσs(‖p-q‖)Gσr(‖Ip-Iq‖)Iq(2)Wp=∑q∈SGσs(‖p-q‖)Gσr(‖Ip-Iq‖)(3)

式中: p、q分别为像素点的空间位置; Ip、 Iq为像素的灰度值; S是以 p为中点的模板区域; Gσs和 Gσr分别代表空间距离和灰度值的高斯核函数; BF[I]p为替换后的模板中心点像素灰度值; Wp为权值系数.

可以看出在双边滤波中采用高斯核直接对原始图像的像素空间距离和像素间灰度值进行处理, 当模板区域中心点为椒盐噪声点时, Wp为零, 因此双边滤波不具有去除椒盐噪声的能力.

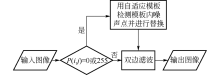
在此基础上, 本文作者提出了先用自适应大小的模板替换方法来替换模板区域内椒盐噪声像素点, 再用高斯核对替换后的模板区域内像素空间距离和像素间灰度值进行处理的方法来改进双边滤波算法.改进后的算法流程如图1所示, 改进后的算法公式为

BF[I]p=1W∧p∑q∈S∧Gσr(‖I∧mp-I∧q‖)I∧q(4)W∧p=∑q∈S∧Gσr(‖I∧mp-I∧q‖)(5)

式中: S∧为替换后的模板区域; I∧mp、 I∧q均为新模板中与 Ip、 Iq相对应像素的灰度值.

改进后的算法对模板中心 p点的灰度值进行了替换, 因此可以有效避免高斯权值过小的问题.

图1 改进后的算法流程图Fig.1 Flow chart of improved algorithm

2.2 自适应大小的模板替换

由于改进算法需要对模板区域像素进行替换如图2所示, 在进行模板替换时, 模板大小的选取将直接影响改进算法对椒盐噪声的滤波效果.如果选取的模板过小, 则在高密度椒盐噪声下, 模板区域内很有可能没有有效像素, 替换后的像素值依然为无效像素, 且当椒盐噪声密度大于70%时这一现象尤为明显, 因此在高密度椒盐噪声的情况下去噪效果很差.如果选取的模板过大, 则在低密度椒盐噪声下滤波时, 距离中心像素点较远的像素值, 会直接影响替换像素的灰度值大小, 即距离中心像素点越远, 则该点像素值与中心像素点的真实灰度值差异可能会越大, 因此选取的模板过大时对低密度椒盐噪声的图片滤波效果较差.

图2 高密度椒盐噪声的Lena图进行模板替换操作Fig.2 Template replacement operated by Lena image with high-density salt-and-pepper noise

采用自适应大小的模板替换方法则可以有效避免这一问题, 以固定模板大小3× 3为例, 对椒盐噪声密度分别为70%、80%、90%的Lena图进行模板替换操作, 效果如图2所示, 可以看到采用自适应模板大小的模板替换方案明显更好, 且椒盐噪声密度越大差异越明显.

以固定模板大小7× 7为例, 对椒盐噪声密度分别为10%、20%、30%的Lena图进行模板替换操作, 效果如图3所示, 可以看到采用自适应模板大小的模板替换方案明显更好, 且椒盐噪声密度越小差异越明显.

图3 低密度椒盐噪声的Lena图进行模板替换操作Fig.3 Template replacement operated by Lena image with low-density salt-and-pepper noise

本文采用自适应大小的模板替换算法, 该算法包括以下3个过程.

1)检测模板中心点是否为椒盐噪声点, 如果是则进行模板替换; 如果不是, 则不改变该点的灰度值.设待处理像素点的灰度值为 P(i, j), 判定公式为

P(i, j)=是, P(i, j)=0或255否, 其他情况(6)

2)自适应调整模板大小.检测模板内是否有非椒盐噪声点, 如果有, 模板大小设定为3× 3; 如果没有, 则扩大模板大小继续检测, 模板最大值设定为7× 7.

3)对模板区域进行裁剪, 删除模板内的噪声点.对剩余像素分类后替换中心像素灰度值.

2.3 模板中心点的替换规则

以3× 3的模板大小为例对中心点的替换规则, 共分为以下两种情况.

1)模板区域内灰度值小于76(0.3倍255)或大于178(0.7倍255)的像素点在所有有效像素点中个数最多.灰度值小于76的像素点最多时, 对灰度值小于76的像素点集合取中值, 用此中值来替换模板中心点的灰度值, 替换方式如图4所示, 图中 C1、 C2、 C3分别表示模板区域内灰度值小于76、灰度值大于178、灰度值介于76至178的像素点个数; 当模板区域内灰度值大于178的像素点在所有有效像素点中个数最多时替换方式与之类似, 对灰度值大于178的像素点集合取中值, 用此中值来替换模板中心点的灰度值.

图4 灰度值小于76的像素点居多时3× 3的模板中心点替换规则Fig.4 Focus replacement operation of 3× 3 template when the majority grey value of pixels is less than 76

2)模板区域内灰度值介于76~178之间的像素点在所有有效像素点中个数最多, 或灰度值小于76、大于178、介于76~178之间的3组像素点集合内某两组的像素点个数相等且大于另一组.此时直接取灰度值介于76~178之间的像素点集合的中值, 用此中值来替换模板中心点的灰度值.

此外, 如果模板大小扩大到7× 7时区域内所有像素点仍均为椒盐噪声点, 则采用模板中心点前一点的替换值来替换模板中心点, 替换方法如图5所示, 其中NA表示不适用.

图5 模板区域没有有效像素点时7× 7的模板中心点替换规则Fig.5 Focus replacement operation of 7× 7 template without valid pixels of the region

按以上步骤遍历图像中所有椒盐噪声点后, 再用双边滤波器的模板从图像右上角遍历图像中所有像素点, 此时双边滤波器选中的模板区域即为模板替换后新的模板区域.

3 实验结果及算法分析

实验在Matlab R2015b平台下完成, 选用的所有图片大小均为512× 512, tiff格式, 对8张不同的图片分别添加了10%~90%的椒盐噪声并进行滤波.

3.1 改进算法实验结果分析

传统的双边滤波由于采用高斯核为基础, 由式(2)不难看出双边滤波算法既类似于传统的高斯滤波采用局部加权平均的思想, 又考虑像素点的空间邻近度关系和像素灰度值的相似性, 通过两者的结合, 能很好地达到保持图像边缘又有效平滑高斯噪声的目的[12].但当模板区域 S的中心点 p为椒盐噪声点时, S内其他点的灰度值 Iq与 p点灰度值 Ip差异很大, 从而导致高斯核 Gσr(‖Ip-Iq‖)极小并趋于0, 因此传统的双边滤波算法不具备去除椒盐噪声的能力.而改进算法可以有效避免高斯核趋于0的情况, 因此在理论上改进算法应在具有传统双边滤波算法保边和去除高斯噪声能力的同时, 可以对椒盐噪声进行有效滤波.

为了验证这一性能, 在图6中给出了3种算法去噪后的图像对比, 对Lena图添加了均值为0, 方差为0.05的高斯噪声, 用改进算法对加噪后的图像进行滤波, 并与双边滤波和高斯滤波进行对比, 表1中给出了3种算法对受不同方差大小高斯噪声污染的Lena图去噪后PSNR和SSIM的大小.3种算法模板大小均为7× 7的矩阵, 双边滤波的空间参数和颜色参数分别为10、0.2, 改进算法的颜色参数为0.2.

图6 3种算法去噪后的图像对比Fig.6 Image comparison of three kinds of denoising algorithm

表1 3种算法去噪后的PSNR和SSIM对比 Tab.1 Comparison between PSNR and SSIM under different for three kinds of denoising algorithms

由图6可以看出相比于高斯滤波, 双边滤波和本文改进算法均有较好的保边能力, 且保边效果一致.由表1可以看出改进算法相较于双边滤波去除高斯噪声的能力几乎相同, 因此认为改进算法保留了双边滤波保边和去除高斯噪声的能力.

为了验证改进算法在双边滤波保边和去除高斯噪声的能力之外还具有去除椒盐噪声的能力, 对Lena添加均值为0, 方差为0.05的高斯噪声, 噪声密度20%的椒盐噪声, 用改进算法和双边滤波分别对加噪后的图像进行滤波并进行对比.滤波结果如图7所示.

图7 含有高斯噪声和椒盐噪声的图像处理效果对比Fig.7 Comparison between the image processing effect with Gaussian noise and the one with salt-and-pepper noise

由图7显然可以看出双边滤波对同时含有高斯噪声和椒盐噪声的图像滤波效果很差, 而本文改进算法的滤波效果明显好于双边滤波.因此认为改进算法保留了双边滤波保边和去除高斯噪声能力的同时具有去除椒盐噪声的能力.

3.2 改进算法与经典算法对比

为了验证改进算法对椒盐噪声的去噪能力, 实验选用8张大小为512× 512的常用图像处理图片, 见图8和图9.对其添加10%~90%密度的椒盐噪声, 并用本文改进算法和DBA、NAFSMF、MDBUTMF、EMF1、EMF2算法对其进行滤波, 给出了滤波后的PSNR和SSIM.图8和9分别给出了几种算法在噪声密度为30%、50%、70%的情况下对Lena图和Peppers图的处理效果, 并给出了相应的结构相似性局部值的分布图.

图8 不同噪声密度下几种算法对Lena图的处理结果Fig.8 Processing results of different algorithms for Lena image under different noise density

图9 不同噪声密度下几种算法对Peppers图的处理结果Fig.9 Processing results of different algorithms for Peppers image under different noise density

1)由图8和9可以看出几种算法在滤波的同时均不会对图像边缘造成过度模糊, 即拥有较好的保边性能.在结构相似性局部值的分布图中, 像素点的颜色越深代表滤波后的图像在这一点的灰度值与原图像差别越大, 因此可以看出在30%、50%、70%的3种噪声密度下改进算法的滤波效果均好于DBA、MDBUTMF、EMF1、EMF2算法, 且噪声密度越高, 该算法的优势越明显, 相比于NAFSMF算法, 改进算法性能好于NAFSMF算法, 但随着噪声密度的提高, 两种算法间的差距逐渐变小.

2)在图10、11中分别给出了不同噪声密度下几种算法的PSNR和SSIM的计算值的折线图, 与其他5种算法相比, 本文提出的改进算法滤波效果更好, 且PSNR平均值提升5.8%以上, SSIM平均值提升2.75%以上.因为使用了自适应模板大小, 本文的改进算法在高椒盐噪声密度下的滤波效果较好.图12、13给出了当椒盐噪声密度为95%时这几种算法的处理结果, 在图12、13中前2张图片分别为Lena和Peppers图原图和加噪后的图像, 后6张依次为DBA、NAFSMF、MDBUTMF、EMF1、EMF2、改进算法的处理结果.

图10 Lena图对应的SSIM和PSNR数据的折线图Fig.10 Line chart of SSIM and PSNR for Lena image under different noise density

图11 Peppers图对应的SSIM和PSNR数据的折线图Fig.11 Line chart of SSIM and PSNR for Peppers image under different noise density

图12 几种算法对椒盐噪声密度为95%的Lena图处理效果对比Fig.12 Processing results of different algorithm for Lena image under 95% of noise density

图13 几种算法对椒盐噪声密度为95%的Peppers图处理效果对比Fig.13 Processing results of different algorithm for Peppers image under 95% of noise density

综合以上的PSNR和SSIM数据, 可以看出在不同椒盐噪声密度下本文提出的改进算法滤波效果均远好于DBA、EMF1、EMF2算法.与MDBUTMF算法相比, 改进算法在低椒盐噪声密度时滤波效果与其相近, 在中高椒盐噪声密度时MDBUTMF算法性能急剧下降, 改进算法滤波效果远好于MDBUTMF算法.与NAFSMF算法相比, 改进算法在中低椒盐噪声密度时滤波效果远好于NAFSMF算法, 在高椒盐噪声密度时NAFSMF算法性能下降较慢, 但改进算法滤波效果仍好于NAFSMF算法.因此认为本文提出的改进算法综合性能好于以上5种算法, 这一结果与主观视觉感受相吻合.

4 结论

1)传统的双边滤波具有良好的保边和去除高斯噪声的能力, 但并不具有去除椒盐噪声的能力.因此本文作者提出了一种先对模板区域像素灰度值进行替换, 再进行双边滤波的方法来改进传统双边滤波算法, 使其具有良好的去除椒盐噪声的能力, 拓宽了双边滤波的应用范围.

2)在Matlab平台下的实验中, 验证了本文作者提出的改进算法的滤波性能, 实验共对8张图像处理领域常用的图片进行了滤波处理.实验结果表明, 在噪声密度10%~90%的情况下与经典算法DBA、NAFSMF、MDBUTMF、EMF1、EMF2相比, 本文提出的改进算法滤波效果更好, PSNR平均值提升5.8%以上, SSIM平均值提升2.75%以上, 且对受到高密度椒盐噪声污染的图像具有更好的滤波效果.

The authors have declared that no competing interests exist.

参考文献
[1] TOMASI C, MANDUCHI R. Bilateral filtering for gray and color images[C]//International Conference on Computer Vision, 1998: 839. [本文引用:1]
[2] PITAS I, VENETSANOPOULOS A N. Order statistics in digital image processing[J]. Proceedings of the IEEE, 1992, 80(12): 1893-1921. [本文引用:1]
[3] KO S J, LEE Y H. Center weighted median filters and their applications to image enhancement[J]. IEEE Transactions on Circuits and Systems, 1991, 38(9): 984-993. [本文引用:1]
[4] WANG Z, ZHANG D. Progressive switching median filter for the removal of impulse noise from highly corrupted images[J]. IEEE Transactions on Circuits & Systems II Analog & Digital Signal Processing, 1999, 46(1): 78-80. [本文引用:1]
[5] SRINIVASAN K S, EBENEZER D. A new fast and efficient decision-based algorithm for removal of high-density impulse noises[J]. IEEE Signal Processing Letters, 2007, 14(3): 189-192. [本文引用:1]
[6] TOH K K V, ISA N A M. Noise adaptive fuzzy switching median filter for salt-and -pepper noise reduction[J]. IEEE Signal Processing Letters, 2010, 17(3): 281-284. [本文引用:1]
[7] ESAKKIRAJAN S, VEERAKUMAR T, SUBRAMANYAM A N, et al. Removal of high density salt and pepper noise through modified decision based unsymmetric trimmed median filter[J]. IEEE Signal Processing Letters, 2011, 18(5): 287-290. [本文引用:1]
[8] JOURABLOO A, FEGHAHATI A H, JAMZAD M. New algorithms for recovering highly corrupted images with impulse noise[J]. Scientia Iranica, 2012, 19(6): 1738-1745. [本文引用:1]
[9] ERKAN U, KILICMANB A. Two new methods for removing salt-and -pepper noise from digital images[J]. ScienceAsia, 2016, 42(1): 28-32. [本文引用:1]
[10] 曾宪佑, 黄佐华. 一种新型的自适应模糊中值滤波算法[J]. 计算机工程与应用, 2014, 50(17): 134-136.
ZENG Xianyou, HUANG Zuohua. New adaptive fuzzy median filtering algorithm[J]. Computer Engineering and Applications, 2014, 50(17): 134-136. (in Chinese) [本文引用:1]
[11] SRINIVASAN K S, EBENEZER D. A new fast and efficient decision-based algorithm for removal of high-density impulse noises[J]. IEEE Signal Processing Letters, 2007, 14(3): 189-192. [本文引用:1]
[12] 张海荣. 双边滤波去噪方法及其应用研究[D]. 合肥: 合肥工业大学, 2014.
ZHANG Hairong. Research on bilateral filtering denoising methods and their applications[D]. Hefei: Hefei University of Technology, 2014. (in Chinese) [本文引用:1]