投射式电容屏触控轨迹Z字形噪声快速滤波算法

引用本文

李居朋, 张祖成, 杨佳烁, 樊磊. 投射式电容屏触控轨迹Z字形噪声快速滤波算法[J]. 北京交通大学学报, 2017,41(5): 37-42.
LI Jupeng, ZHANG Zucheng, YANG Jiashuo, FAN Lei. Fast filtering algorithm for zigzag noise of touch tracking of capacitive touch panels[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2017,41(5): 37-42.
Doi:10.11860/j.issn.1673-0291.2017.05.006 复制到剪切板

Permissions

北京交通大学学报编辑部所有

投射式电容屏触控轨迹Z字形噪声快速滤波算法

李居朋¹, 张祖成¹, 杨佳烁¹, 樊磊²

1.北京交通大学电子信息工程学院,北京 100044

2.北京集创北方科技股份有限公司,北京 100088

第一作者:李居朋(1981—),男,江苏沛县人,副教授,博士. 研究方向为信号与信息处理和图像处理.email:lijupeng@bjtu.edu.cn

收稿日期: 2017-03-23

基金: 国家自然科学基金项目(81671034); 北京市科技计划项目(D151100000415002)

摘要

投射式电容触摸屏(Capacitive Touch Panels,CTP)已成为智能终端人机交互界面的主流. 针对屏体电极排布空隙造成的触控轨迹Z字形干扰问题,提出了一种基于IMAF模型的触控轨迹快速平滑滤波算法. 通过触摸屏原始触控轨迹Z字形噪声特征与成因分析,以此建立适用于触控轨迹Z字形脉冲性干扰的非线性滤波模型,经时域串行轨迹数据的先入先出快速迭代处理,实现电容屏触控轨迹的平滑处理. 实验测试结果证明:该算法兼具线性和统计滤波模型的滤波处理能力,相比传统触控轨迹滤波算法,可有效实现触控轨迹Z字形噪声的平滑处理.

关键词: 信号处理; 电容触摸屏; Z字形噪声; IMAF模型; 轨迹平滑

中图分类号:TN911.7

Fast filtering algorithm for zigzag noise of touch tracking of capacitive touch panels

LI Jupeng¹, ZHANG Zucheng¹, YANG Jiashuo¹, FAN Lei²

1.School of Electronic and Information Engineering, Beijing Jiaotong University, Beijing 100044,China

2. Chipone Technology (Beijing) Co., Ltd., Beijing 100088, China

Fund:National Natural Science Foundation of China(81671034); Beijing Science and Technology Plan Project(D151100000415002)

Abstract

Capacitive Touch Panels(CTP) have become the mainstream of human-computer interaction interface in intelligent terminal. Generally, zigzag noise of touch tracking caused by voidage distribution of screen eletrode makes impact on the accuracy of predictions of touch positions. A fast smooth processing algorithm for capacitive touch panels based on IMAF filter model has been proposed in this paper. Non-linear filter model applicable to zigzag pulse interference of touch tracking has been established on the basis of characteristic and genetic analysis of zigzag noise of original touch tracking in touch panels. Temporal serial trajectory data is processed by a first-in first-out fast iterative method so as to achieve the smooth processing of touch tracking of capacitive touch panels. Experimental results have indicated that this proposed algorithm has the capacity of linear and statistical filter processing. Compared with traditional filtering algorithm of touch tracking, this proposed algorithm can achieve effective smooth processing for zigzag noise of touch tracking.

Keyword: signal processing; capacitive touch panel; zigzag noise; IMAF model; smooth trajectory

文章图片

随着iPhone等智能终端电子产品的强势推出, 所采用的投射式电容触摸屏也成为了终端产品首选人机交互界面. 严格地讲, 电容触摸屏技术还并不是一个完全成熟的技术. 基于互电容感应原理的多点触摸, 驱动电极与感应电极的交叉点处产生的寄生电容值非常低, 通常处于0.2~4 pF级别, 而手指触摸产生的互电容变化量更加微弱, 同时面临着周围诸多噪声源的干扰, 在此情况下准确快速定位触控轨迹是摆在触控设计者面前的一大难题^[1]. 如LCD噪声、外界电磁波噪声、USB充电器噪声、静电释放(Electro-Static Discharge, ESD)噪声等都是触控设计中不可回避的干扰源.如何使触摸屏系统对各种噪声源的噪声, 有很好的免疫能力以获得足够高的信噪比是电容触摸屏的设计挑战^[2]. 尽管文献[3, 4, 5, 6]从触控芯片硬件设计角度提出了多种特殊结构的电路, 如基于微分检测方法的触摸控制电路、滤波电路及匹配补偿电路等用于降低触控电容检测误差、提高电压检测动态范围, 但是利用硬件抑制噪声要比软件算法困难得多, 因此滑动平均滤波(Moving Average Filter, MAF)算法常被用来降低测量噪声误差和定位触摸位置失真^[7], 但仅适用于等幅的随机波动噪声抑制场合, 还有一类是由于触控屏体电极结构设计带来的脉冲性干扰噪声, 表现为高频非线性震荡特性, 即投射式电容屏触控轨迹Z字形噪声类型, 为了获得可接受的噪声滤波性能, 研究者通过增加MAF采样点用于抑制该种类型的噪声^[7], 势必导致触控轨迹的偏移、位置报点的延迟及算法实现成本的增加.

本文作者针对MAF算法在处理触控轨迹Z字形噪声中存在的局限问题, 提出了一种改进的滑动平均滤波(Improved Moving Average Filter, IMAF)算法用于电容屏触控轨迹Z字形的快速滤波处理, 根据触控轨迹平均平滑度定义分析算法参数设置与滤波性能的关系, 以此给出适用于实际电容触控系统的触控轨迹平滑算法.

1 触控轨迹Z字形噪声特征分析

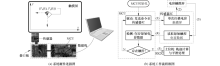
触控数据采集系统由电容式触摸屏、触控传感器IC、微控制器单元MCU和数据接口板组成, 如图1(a)所示, 触摸屏包含 $m \times n$ 菱形分布ITO电极, 用于检测电容触摸屏的电容并产生原始数据. 触控传感器IC接收扫描命令完成CTP的单次扫描, 数据经过A/D转换器产生原始的触控电容数据, MCU实现是否存在触摸的判断, 若存在触摸则将计算获得的触控位置坐标数据经串口发往上位机, 实际工作流程如图1(b)所示.

	Figure Option View Download New Window
	图1 触控信号采集系统Fig.1 Touch signal acquisition system

触控传感器IC单次扫描触摸屏获得的数据反映了当前状态下面板所有交叉节点处的电容, 假设电容触摸屏由m个驱动电极和n个感应电极组成, 从而形成k时刻m× n的交叉互电容矩形阵列为

$C (k) = {[\begin{array}{l} C_{11} & \dots & C_{1 n} \\ ︙ & ⋱ & ︙ \\ C_{m 1} & \dots & C_{mn} \end{array}]}_{m \times n} (1)$

寻找采样k时刻电容数据帧中的最大值, 坐标位于点P_max (k)=(P_maxx(k), P_maxy (k)), 当该最大值大于设置的阈值T时可判定真实触控的开始(阈值T一般依据触摸信号采集的硬件系统而定), 此时触控点可由原始电容数据帧中以P_max (k)坐标为中心的邻域Ω 内的电容值加权计算得到, 坐标记为P(k)=(P_x (k), P_y (k))为

$\{\begin{array}{l} P_{x} (k) = \frac{\sum_{x \in Ω} \sum_{y \in Ω} C_{xy} \cdot {(P}_{\max, x} (k) + x)}{\sum_{x \in Ω} \sum_{y \in Ω} C_{xy}} \\ P_{y} (k) = \frac{\sum_{x \in Ω} \sum_{y \in Ω} C_{xy} \cdot {(P}_{\max, y} (k) + y)}{\sum_{x \in Ω} \sum_{y \in Ω} C_{xy}} \end{array} (2)$

式中: $x 、 y$ 为触摸屏上的坐标(坐标系如图1(a)中标注); $C_{xy}$ 表示对应点上的电容值.将一次完整的手指触控过程记录获得的坐标点按照采样时刻k串行排列, 即组成电容屏触控轨迹信号P(k), k=1, …, N, 给出了触控过程在显示坐标系下的轨迹曲线如图2所示, 可以看出触控轨迹的脉冲尖峰以40像素为间隔近似均匀分布于 $x$ 轴坐标420~740之间.

	Figure Option View Download New Window
	图2 含有Z字形噪声的触控轨迹曲线Fig.2 Touch track curve including zigzag noise

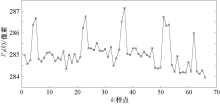
触控轨迹Z字形噪声的成因分析:触控信号的检测易受到来自不同方面的不同噪声源的干扰, 一般的触控抖动、充电器与液晶显示器(TFT-LCD)是最为常见和影响最为明显的噪声来源, 噪声通过复杂的耦合途径干扰生成触控轨迹曲线上的等幅微小波动的噪声, 从而影响电容屏触控轨迹的定位精度. 图2显示了典型的触控Z字形轨迹曲线, 轨迹Z字形冲激突起近似均匀地分布于整条轨迹当中, 这部分折线出现位置正与 $x$ 轴上的驱动电极排布相对应. 因此可以分析出触控轨迹Z字形噪声形成的原因:当手指连续划线处于两电极块连接处时, 由于电极块排布空隙(GAP)造成了不连续的金属层, 相当于电容两极板对应面积的减小, 使得寄生电容值的突变, 从而造成了电容变化的不连续, 反映在触控轨迹中出现了Z字形噪声.

2 Z字形噪声快速滤波算法

2.1 滑动平均滤波算法MAF

滑动平均滤波又称递推平均滤波, 对于数据P(k)是将待处理数据中长度为M的队列放入同一缓冲区内, 求其平均值作为当前时刻的滤波值, 该种滤波算法最主要的特点在于实现的简捷性, 尤其可采用先入先出的递推形式计算, 在触控轨迹噪声滤波中获得了广泛应用. MAF模型是一种有限长脉冲响应(Finite Impulse Response, FIR)滤波器, 滤波模型^[8]为

$\overset{\land}{P} (k) = \frac{1}{M} \overset{M - 1}{\sum_{i = 0}} P (k - i) (3)$

显然MAF滤波器是一种线性滤波器, 从而决定了MAF无法适用于存在脉冲性干扰的滤波应用场合, 不易消除由于脉冲干扰所引起的采样值偏差^[9]. 而从触控轨迹(图2)可以看出电容触控屏中的Z字形噪声正是由于轨迹中的脉冲性波动形成, 如何设计一种适用于处理触控轨迹Z字形噪声的滤波算法, 本文提出了一种改进的滑动平均滤波模型, 实现触控轨迹中的非线性滤波处理.

已知动态测试数据P(k)是由确定性成分P₀ (k)和随机性成分n(k)叠加而成, P₀ (k)为所需的测量结果或有效信号, n(k)为随机起伏的测试误差或噪声, 从而相应将动态测试数据写成为

$P (k) = P_{0} (k) + n (k) (4)$

由分析可知传统MAF算法无法应对脉冲性干扰, 那么一般的滑动平均模型是沿全长为N的数据P(k)逐个滑动读取M个相邻数据作加权平均计算为

$\overset{\land}{P} (k) = \overset{M - 1}{\sum_{i = 0}} w (i) P (k - i) (5)$

式中, w(i)为模型加权系数, 且满足以下条件为

$\overset{M - 1}{\sum_{i = 0}} w (i) = 1 (6)$

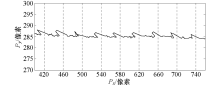
加权系数取值的不同就形成了多种性能各异的滑动平均算法. 当w(i)=1/M时, 一般的滑动平均模型简化为式(3)的等权滑动平均算法.分离出图2中触控轨迹的y方向上的分量P_y (k), 等间隔画出分量P_{_}y (k)~k曲线如图3所示.

	Figure Option View Download New Window
	图3 触控轨迹分量P_y(k)~k的曲线Fig.3 Curve diagram of touch track component P_y(k)~k

可以看出触控轨迹中的Z字形噪声在P_y(k)~k的曲线图的体现, 在P_y (k)~k的曲线中存在着近似均匀分布的非线性的脉冲噪声, 同时该曲线中脉冲干扰中间部分为较小幅度的随机性噪声, 从而看出单纯使用等权滑动平均法可以很好地处理较小幅度的随机性噪声, 而无法抑制较大幅度变换的脉冲性噪声, 即触控轨迹Z字形干扰噪声.

2.2 IMAF模型的触控Z字形噪声滤波算法

非线性滤波模型中最为典型的是中值滤波模型, 具有良好的边缘保持特性和抑制脉冲噪声的能力^[10]. 动态测试数据P(k), k=1, 2, …, N, 类似于滑动平均滤波处理过程, 逐个滑动读取M个相邻数据, 特别的, 这里M值一般为奇数, M=2d+1, 则在第i时刻, 窗口内经从小到大顺序排列的数据队列表示为W_d (i)={P(i-d), …, P(i), …, P(i+d)}, 选取中位值作为滤波后的数据 $\overset{\land}{P} (i) = Med {{W}_{d} (i)},$ 采用先进先出原则实现所有数据的噪声抑制. 通过选择适当的窗口宽度, 中值滤波能够有效地降低信号中的脉冲噪声, 但对于具有随机性波动噪声的处理能力较MAF模型弱.

为了使得等权滑动平均模型具有处理脉冲性噪声的非线性滤波能力, 基于中值滤波模型的数据统计思想, 提出了基于IMAF模型的触控轨迹Z字形噪声的快速滤波算法, 从一般形式的滑动平均滤波模型式(5)演变而来, 设计如下的滑动平均滤波模型的加权参数为

$w (i) = \{\begin{array}{l} 0, i = \arg (L_{m} W_{d} (i)) \\ 0, i = \arg (R_{m} W_{d} (i)) \\ 1 / (M - 2 m), i = 其他 \end{array} (7)$

式中: L_m, R_m 表示左右各取m个点子序列.

该模型参数结合了等权滤波模型和中值统计模型两个方面的设计:1)对于第 $i$ 时刻经从小到大顺序排列的数据队列W_d (i)中最大值、最小值所对应的加权系数w(i)=0, 这样IMAF模型则具有了数据统计滤波模型中的处理脉冲性噪声的能力; 2)对于第i时刻经从小到大顺序排列的数据队列W_d (i)中极值之外所对应的加权系数w(i)=1/(M-2m), 也就是求其等权加权均值, 使得IMAF模型具备处理随机波形噪声的能力.

3 IMAF算法性能的测试与分析

算法性能测试实验选用一块7寸由20× 12菱形分布ITO电极组成的电容式触摸屏, 采集获取多组触控原始数据, 以CSV文件格式存储用于后续的数据处理. 为衡量本文提出基于IMAF模型的触控轨迹Z字形噪声平滑滤波算法, 这里同时选取MAF、中值滤波方法进行效果、速度的对比分析. 实验环境参数为:Intel(R) Xeon(R) CPU E5-2630v3 @2.40 GHz, 32 GB RAM, 64位Windows7, MATLAB 2014.

3.1 Z字形噪声平滑滤波的定性分析

截取图3触控轨迹中3段含有Z字形的数据片段, 分别进行3种不同的平滑滤波算法处理, 图4给出了对应的轨迹平滑处理结果对比. 从图4中可以看出IMAF滤波结果在Z字形噪声附近处理的结果, 对比MAF结果更为平滑, 也就进一步验证了算法设计中利用数据统计功能的非线性模型在处理Z字形脉冲性噪声干扰性能设计的有效性; 同时IMAF滤波结果在Z字形噪声之外的数据区域, 对比中值滤波处理轨迹曲线, 使得滤波处理后的曲线在取得较好的平滑度的情况下, 滤波结果曲线位于原始数据曲线之间的范围, 这也验证了IMAF滤波模型同时具有了MAF平滑处理较小幅度的随机性噪声的能力.

	Figure Option View Download New Window
	图4 触控轨迹Z字形噪声滤波结果对比Fig.4 Comparison of filtering results for zigzag noise of touch tracking between different algorithms

3.2 Z字形噪声平滑滤波的定量分析

为了从定量上衡量不同算法在触控轨迹平滑方面的性能, 这里通过定义触控轨迹上的 $k$ 时刻轨迹平滑度(Tracking Smoothness)评价参数实现, 以 $y$ 方向给出定义

$\begin{array}{l} D_{y} (k) = |P_{y} (k) - P_{y} (k - 1)| (8) \\ A_{y} (k) = |D_{y} (k) - D_{y} (k - 1)| (9) \end{array}$

同理可以得到x方向上的评价参数D_x (k)和A_x (k), 则触控轨迹k时刻的单点平滑度定义为

$S (k) = A_{x} (k) + A_{y} (k) (10)$

衡量整个触控数据P(k), k=1, …, N的轨迹平滑度, 可由单点平滑度参数S(k)计算触控轨迹的平均平滑度为

$S_{avg} (k) = \frac{1}{N - 2} \overset{N}{\sum_{k = 3}} S (k) (11)$

图4直观的给出了3种不同滤波算法对原始触控轨迹的平滑滤波结果, 直观上看出:1)MAF算法较好地平滑了轨迹中的随机波动噪声而无法很好处理Z字形尖峰; 2)中值滤波方法在抑制Z字形噪声的同时造成了轨迹曲线的显著偏移; 3)本文滤波算法综合了以上两种方法的优点, 很好地拟合了整条轨迹曲线. 从实际采集的电容屏触控数据中随机选取8条 $(T_{1} ~ T_{8})$ 触控轨迹曲线, 经3种方法处理的定量性能分析, 包括轨迹平滑度参数和计算时间的对比如表1所示.

表1 轨迹平滑度与时间对比(轨迹平滑度/时间:ms) Tab.1 Comparison of tracking smoothness and computing time (Tracking smoothness/Computing time: ms)

由触控轨迹平均平滑度参数的定义可知, 轨迹的 $S_{avg}$ 参数值越小, 则表示该触控轨迹越平滑, 而对于同一条触控轨迹数据, 不同算法间的 $S_{avg}$ 参数值越小, 说明该触控轨迹噪声抑制效果越好. 表1给出3种轨迹平滑滤波处理后的轨迹 $S_{avg}$ 参数值和计算时间对比, 可以看出:1)本文IMAF算法取得的轨迹平均平滑度参数最小, 相对于MAF算法处理结果有较大的提高, 而中值滤波算法获得的平均平滑度参数是3种方法中效果最差; 2)本文IMAF算法由于采用了先入先出的迭代数据处理模式, 相比于MAF算法减少了部分求和运算, 而中值滤波为了取得可接受的平滑度则选择了更大的数据窗口, 所消耗的计算时间最长. 为了进一步比较3种处理算法的性能, 将30条原始触控轨迹平滑处理后的参数求其平均值见表2.

表2 不同轨迹噪声抑制算法性能参数对比 Tab.2 Comparison of performance parameters between different algorithms ms

轨迹平滑算法	$S_{avg}$ 平均值	$S_{avg}$ 均方差	计算时间平均值
MAF滤波算法	0.224 0	0.024 8	95.52
中值滤波算法	0.587 2	0.123 3	110.96
IMAF滤波算法	0.135 5	0.020 4	83.90

表2 不同轨迹噪声抑制算法性能参数对比 Tab.2 Comparison of performance parameters between different algorithms ms

本文用于触控Z字形噪声的非线性滤波模型获得了更好的轨迹平滑度, 消耗计算时间较基于MAF模型的滤波算法有效减少了12%, 从而进一步验证了本文IMAF算法的有效性和稳定性.

4 结论

投射式电容屏触控轨迹中Z字形噪声是影响触控质量的最大因素, 通过适合的处理方式获得较为平滑的触控轨迹, 是获得良好触控体验的基础.

1)本文作者在分析轨迹噪声特征的基础上, 提出了能够适用于Z字形脉冲干扰噪声的IMAF算法, 实验定性与定量的结果分析表明:本文算法与MAF、中值滤波算法相比, 本文IMAF算法可以获得最好的轨迹平滑度.

2)本文IMAF算法在有效减少计算时间的情况下, 获得了更好触控轨迹Z字形噪声抑制效果, 适用于投射式电容触摸屏系统的应用.

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	张晋芳, 陈后金, 曲孔宁. 自互一体式电容触摸屏检测电路设计[J]. 北京交通大学学报, 2016, 40(2): 36-40. ZHANG Jinfang, CHEN Houjin, QU Kongning. A self-cap and mutual-cap detection circuit for capacitive touch panel[J]. Journal of Beijing Jiaotong University, 2016, 40(2): 36-40. (in Chinese) [本文引用:1]
[2]	詹思维, 魏廷存, 李博, 等. 投射式电容触摸屏控制芯片设计[J]. 微电子学, 2013, 43(3): 364-368. ZHAN Siwei, WEI Tingcun, LI Bo, et al. Design of a sensor controller IC for projected capacitive touch panel[J]. Microelectronics, 2013, 43(3): 364-368. (in Chinese) [本文引用:1]
[3]	HEO S, MA H, SONG J, et al. 72 dB SNR, 240 Hz frame rate readout IC with differential continuous-mode parallel architecture for larger touch-screen panel applications[J]. IEEE Transactions on Circuits and Systems I, 2016, 63(7): 960-971. [本文引用:1]
[4]	RAGHEB A N, MOHAMED M G A, KIM H W. Differentiator based sensing circuit for efficient noise suppression of projected mutual-capacitance touch screens[C]// International Conference on Electronics, Information, and Communications, 2016: 1-5. [本文引用:1]
[5]	LEE J S, YEO D H, KWON H J, et al. An ICD-VCOM-noise resilient mutual-capacitive touch-sensor IC chip with a low-voltage driving signal[J]. IEEE Sensors Journal, 2015, 15(8): 4595-4602. [本文引用:1]
[6]	YEO D H, KIM S H, NOH H K, et al. A SNR-enhanced mutual-capacitive touch-sensor ROIC using an averaging with three specific TX frequencies, a noise memory, and a compact delay compensation circuit[J]. IEEE Sensors Journal, 2016, 16(18): 6931-6938. [本文引用:1]
[7]	GAO S, MCLEAN D, LAI J, et al. Reduction of noise spikes in touch screen systems by low pass spatial filtering[J]. Journal of Display Technology, 2016, 12(9): 957-963. [本文引用:2]
[8]	裴益轩, 郭民. 滑动平均法的基本原理及应用[J]. 火炮发射与控制学报, 2001(1): 21-23. PEI Yixuan, GUO Min. The fundamental principle and application of sliding average method[J]. Gun Launch & Control Journal, 2001 (1): 21-23. (in Chinese) [本文引用:1]
[9]	杨慧, 许福栗. 基于权重转移的加权滑动平均模型改进[J]. 计算机工程与应用, 2014, 50(14): 156-159. YANG Hui, XU Fuli. Improvement of weighted moving average model based on transferring weights[J]. Computer Engineering and Applications, 2014, 50(14): 156-159. (in Chinese) [本文引用:1]
[10]	BHADOURIA V S, GHOSHAL D, SIDDIQI A H. A new approach for high density saturated impulse noise removal using decision-based coupled window median filter[J]. Signal, Image and Video Processing, 2014, 8(1): 71-84. [本文引用:1]

2016

0.0

... 2~4 pF级别,而手指触摸产生的互电容变化量更加微弱,同时面临着周围诸多噪声源的干扰,在此情况下准确快速定位触控轨迹是摆在触控设计者面前的一大难题^[1] ...

2013

0.0

... 如何使触摸屏系统对各种噪声源的噪声,有很好的免疫能力以获得足够高的信噪比是电容触摸屏的设计挑战^[2] ...

2016

0.0

... 尽管文献[3,4,5,6]从触控芯片硬件设计角度提出了多种特殊结构的电路,如基于微分检测方法的触摸控制电路、滤波电路及匹配补偿电路等用于降低触控电容检测误差、提高电压检测动态范围,但是利用硬件抑制噪声要比软件算法困难得多,因此滑动平均滤波(Moving Average Filter,MAF)算法常被用来降低测量噪声误差和定位触摸位置失真^[7],但仅适用于等幅的随机波动噪声抑制场合,还有一类是由于触控屏体电极结构设计带来的脉冲性干扰噪声,表现为高频非线性震荡特性,即投射式电容屏触控轨迹Z字形噪声类型,为了获得可接受的噪声滤波性能,研究者通过增加MAF采样点用于抑制该种类型的噪声^[7],势必导致触控轨迹的偏移、位置报点的延迟及算法实现成本的增加 ...

2016

0.0

2015

0.0

2016

0.0

2016

0.0

2001

0.0

... MAF模型是一种有限长脉冲响应(Finite Impulse Response,FIR)滤波器,滤波模型^[8]为 ...

2014

0.0

... 显然MAF滤波器是一种线性滤波器,从而决定了MAF无法适用于存在脉冲性干扰的滤波应用场合,不易消除由于脉冲干扰所引起的采样值偏差^[9] ...

2014

0.0

... 2 IMAF模型的触控Z字形噪声滤波算法非线性滤波模型中最为典型的是中值滤波模型,具有良好的边缘保持特性和抑制脉冲噪声的能力^[10] ...