引用本文
蔡永林, 马烨萌. 基于冗余自由度的数控加工轨迹运动分解[J]. 北京交通大学学报, 2017,41(4): 111-114.
CAI Yonglin, MA Yemeng. Motion decomposition for NC machining path based on redundant degree of freedom[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2017,41(4): 111-114.
Doi:10.11860/j.issn.1673-0291.2017.04.016  
Permissions
Copyright©2017, 北京交通大学学报编辑部
北京交通大学学报编辑部 所有
基于冗余自由度的数控加工轨迹运动分解
蔡永林, 马烨萌
北京交通大学 机械与电子控制工程学院,北京 100044

第一作者:蔡永林(1968—),男,陕西岐山人,教授,博士,博士生导师. 研究方向为复杂曲面数控加工技术.email:ylcai@bjtu.edu.cn

收稿日期: 2016-05-06
基金: 国家自然科学基金(51375040)
摘要

为降低曲面数控加工中机床运动轴的冲击,提出了采用具有冗余自由度的数控机床实现复杂曲面高速进给加工的思路,通过增加数控机床冗余自由度运动轴,以分解冲击较大机床轴的运动.本文对冗余自由度下机床各轴之间的运动分解原理进行分析,给出了冗余自由度下合成加工轨迹的计算和误差确定方法,并以计算实例验证了所提出思路和方法的有效性.

关键词: 曲面数控加工; 冗余自由度; 运动分解; 高速进给
中图分类号:TG659
Motion decomposition for NC machining path based on redundant degree of freedom
CAI Yonglin, MA Yemeng
School of Mechanical, Electronic and Control Engineering, Beijing Jiaotong University, Beijing 100044,China
Fund:Foundation item:National Natural Science Foundation of China (51375040)
Abstract

In order to reduce the shock of machine motion axis in surface numerical control(NC) machining,the method of using machine tool with redundant degree of freedom(DOF) in high speedfeed complex surface machining is proposed in this paper.The motion axis of redundant degree of freedom in numerical control is added to decompose the movement of machine tool axis with greater impact. In this paper, the decomposition principle of the movement of machine tool axis under redundant DOF is analyzed so as to provide the method of synthesized machining path calculation and error determination under the condition of redundant degree of freedom. Finally,the result of calculation example has verified the effectiveness of the idea and method proposed in this paper.

Keyword: surface NC machining; redundant degree of freedom; motion decomposition; high speed feed

复杂曲面在航空航天、能源动力、汽车、模具等行业得到了广泛应用, 由于形状复杂, 目前这些曲面零件主要在多轴数控机床上加工.在多轴的高速数控加工中, 由于曲面曲率的变化, 机床各运动轴的速度和加速度加大, 机床运动部件的惯性变大, 导致机床的运动部件产生较大的冲击和振动, 影响加工表面质量, 同时也限制了进给速度的进一步提高.

为了提高加工中机床运动的平稳性, 众多学者在刀轴矢量的控制与优化上进行了大量的研究.章永年等[1]综合考虑刀轴矢量光顺性、机床运动平稳性及切削条件稳定等因素, 根据刀轴矢量在不同坐标系下的度量指标, 提出了最优刀轴矢量规划算法.陈金成等[2]研究了机床沿曲线高速加工时的运动学特性和动力学特性, 确定了最大安全进给速度和加速度.HO等[3]首先确定典型位置符合机床运动学特性的刀轴矢量, 然后采用插值得到中间位置刀轴矢量并进行碰撞检查, 得到均匀的刀轴矢量.HU等[4]研究了降低五轴数控加工中旋转轴最大角加速度的刀具轨迹生成方法, 通过在刀轴可行域中反复迭代求取优化刀轴矢量的前倾角和侧偏角, 以达到降低最大角速度的目的.罗明等[5]对前者做了改进, 将刀轴矢量的变化和走刀步长结合起来, 使优化后的刀轴矢量不发生碰撞且变化均匀.HO等[6]和P.BROOMHEAD等[7]分别采用框架思想规划刀轴矢量, 根据若干个初始无干涉刀轴矢量, 利用样条插值方法生成其他光顺、无干涉刀轴矢量.JUN等[8]提出了在每个接触点搜索合适的刀轴方向, 使残留高度最小来解决干涉、刀轴矢量变化大的问题.毕庆贞等[9]针对球头铣刀的曲面五轴加工, 在进给和相邻行两个方向上提出了对刀轴矢量进行整体光顺的模型与算法.张立强等[10]提出了五轴侧铣球头铣刀的运动学模型, 采用多约束适应控制策略优化刀轴运动.Wang等[11]在角速度限制条件下, 通过计算每一个接触点处的刀轴可达范围和无干涉范围之间的交集来确定五轴加工中的刀轴矢量, 为五轴加工中刀轴矢量的优化问题提供了一个较为系统的解决方案.

上述研究对刀位轨迹的光顺性做了优化, 提高了机床运动的平稳性.但如果进一步提高进给速度, 现有的轨迹规划方法存在一定的局限性.为了提高进给速度, 避免高速进给情况下机床的冲击, 最大限度地发挥多轴数控机床的高效、精密优势, 需要寻找更适合高速进给加工的刀位轨迹规划方法.事实上, 在曲面的高速进给数控加工中, 机床各轴的运动并不均衡.通常是某一个运动轴存在振动冲击, 而其他轴并不存在冲击.如果设法将存在冲击轴的进给运动量降低, 在其他切削条件许可的情况下, 整体进给速度有望不降低或进一步提高.基于这一思考, 本文作者提出将运动量过大的轴的运动分解到两个或两个以上的运动轴来完成加工, 即采用具有冗余自由度的机床加工.

1 冗余自由度轴概念的提出

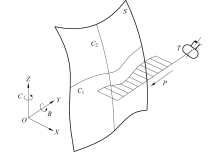
如图1所示, 定义被加工曲面为S, 数控加工机床三个平移轴分别为X、Y和Z轴, 两个回转轴为B轴和C轴, P为刀具T的初始直线加工轨迹, C1和C2 为接触点轨迹.为了实现曲面上某一轨迹(例如C1)的加工, X、Y轴联动可以实现, 但如果Y轴超过了机床本身允许的速度和加速度, 引起了较大的冲击, 则可以考虑增加回转轴C分解Y轴的运动.这种情形中, C轴与X、Y轴之间出现了冗余自由度, C轴即称为冗余自由度轴.同时要考虑到C轴的运动与X、Y轴的运动是关联的, 即刀具为了到达某加工轨迹上给定点, C轴的回转角度与X、Y轴的平移量要满足一定关系.类似地, B轴与X、Z轴之间也存在冗余.

图1 冗余自由度下曲面加工示例Fig.1 Surface machining example under the redundant DOF

我们认为一般可采用具有冗余自由度的机床实现高速进给加工, 将冲击轴的运动量分解到其他轴上, 以减轻冲击.如理论上三坐标机床加工的零件能采用四坐标、五坐标加工, 四坐标机床加工的零件能采用五坐标机床加工.这表面上看似提高了加工成本, 但却能有效降低机床运动轴的冲击, 提高机床运动轴的速度, 实现高速、高效加工.

一般情况下, 任意空间曲面的加工可以视为机床不同坐标平面加工轨迹的合成.对于每个坐标平面内的加工轨迹, 利用机床的2个进给轴联动即可完成, 如2个平移轴联动, 或者1个平移轴和1个回转轴联动.对于确定的机床坐标平面内加工轨迹, 机床2个轴上的运动分量是唯一确定的.

如果在机床坐标平面内再增加1个轴, 则出现了冗余轴.这种情况下, 对于确定的机床坐标平面内加工轨迹, 机床3个轴上的运动分量则不是唯一的, 各轴的运动是关联的, 称这3个轴互为关联轴.任意一轴相对于关联轴内另外2个运动轴来说就是冗余自由度轴.冗余自由度轴可以是关联轴中的平移轴, 也可以是回转轴.由于每个坐标平面内关联轴的运动分量不唯一, 形成了对冗余自由度下机床各轴运动调整的理论依据.

2 冗余自由度下机床运动分解原理

关联轴中各轴的运动是互相影响和制约的, 为了保证机床在高速进给加工时无冲击, 机床各运动轴均必须具有良好的运动规律.

冗余自由度的增加, 会影响其他各轴的运动特性, 因此需要对冗余自由度下机床各轴运动分解原理进行分析.

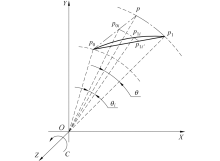
以O-XY平面内某段加工轨迹为例, 机床运动分解原理如图2所示, 某相邻两刀位点为p0(p0x, p0y, p0z)、p1 (p1x, p1y, p1z), 按传统刀位规划思路, 由刀具直接沿X、Y轴联动形成的p0 p1 直线运动实现.如果此时X轴的进给运动超过了机床的允许范围, 引起较大的冲击.

图2 O-XY平面内机床运动分解原理Fig.2 Motion decomposition principle on O-XY coordinate plane

按照本文提出的思路, 增加回转轴C, 来分担X轴的运动.实际加工轨迹为由沿p0p的直线运动(X、Y轴联动)与沿弧pp1的旋转运动(C轴回转, 回转角度为θ )合成, 其中p点坐标为(px, py, pz).此时X、Y、C三轴合成的实际加工轨迹为p0 p1 弧线段.对比无冗余自由度时, X、Y两平移轴合成的加工轨迹p0 p1 直线段, 两不同加工轨迹存在一定偏差.在无冗余轴的情况下, 机床X、Y轴的运动量dx、dy分别为

dx1=p1x-p0x, dy1=p1y-p0y(1)

而在有冗余轴C轴的情况下, 机床X、Y轴的运动量dx、dy分别为

dx2=px-p0x, dy2=py-p0y(2)

从式(1)和式(2)知, dx1< dx2, dy1> dy2.即由于冗余轴C轴的加入, 机床X、Y轴的运动量发生了变化.

在冗余自由度下, pp1弧线段的端点p1, 可视为在时间t内, p0点先由X、Y轴联动运动到p点, 再由C轴回转角度θ 到达p1点, 角度θ 为Op与Op1的夹角.而实际上, 在时间t内X轴、Y轴和C轴是同时运动的, 因此实际加工轨迹为p0p1弧线段.类似地, 对于p0p1弧线段上每一点p1i点, 可视为在时刻ti, X和Y轴联动到达p0i点, 然后C轴旋转θ i到达p1i点, 其中θ i为Op0i与Op1i的夹角.则在时刻ti有

p0i=p0+p-p0·ti/t　(0< ti< t)(3)

三轴实际合成点p1i(p1ix, p1iy)是将点p0i(p0ix, p0iy)绕z轴旋转-θ i倒角得到的, 点p1i坐标值的计算公式有

p1ixp1iy1=p0ixp0iy1×cosθi-sinθi0sinθicosθi0001(4)

式中: θi=θ·ti/t.

而在ti时刻, 无冗余自由度时, X和Y轴联动到达p1i'点, 该点位于p0p1直线上, 其坐标为

p1i'=p0+p1-p0·ti/t(5)

即分别在有无冗余自由度加工时, 在同一时刻, 两不同加工轨迹间存在一定的偏差.

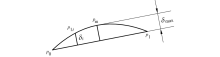
加工轨迹误差如图3所示, 设曲线上点p1i到线段p0p1的距离为δ i, 则δ i即为ti时刻点p1i的轨迹偏差.由于在实际加工中, 线段p0p1的距离并不长, 从工程计算角度考虑, 可取曲线段p0p1的中点pm到线段p0p1的距离作为最大偏差δ max.

图3 加工轨迹误差Fig.3 Machining path error

以上对O-XY平面内X、Y、C这一组关联轴间的运动分解原理进行了分析, 其他坐标平面内各关联轴间运动分解原理与此类似.

3 计算实例

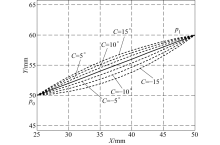
设某段数控加工轨迹为起点p0(25, 50), 终点p1(50, 60), 根据式(4), 利用Matlab软件编写程序分别计算了在有、无冗余轴情况下的加工轨迹情况, 计算结果如图4和表1所示.其中, 图4为增加冗余轴前后的合成轨迹对比, 表1为增加冗余轴前后机床各轴的运动量.在无冗余轴的情况下(也可视为C轴转角为0), X、Y轴联动, 其合成轨迹为直线段p0p1, 如图4中的实线所示.在增加C轴作为冗余轴的情况下, 合成轨迹如图4中的虚线所示.图中分别绘制出了当C轴转角θ =15° 、θ =10° 、θ =5° 、θ =-5° 、θ =-10° 以及θ =-15° 时的合成轨迹, 其中C轴逆时针旋转时θ 的转角为正, 否则为负.

图4 冗余自由度下合成轨迹Fig.4 Synthesis path under the redundant DOF

表1 冗余自由度下各轴的运动量 Tab.1 Motion measurement of each axis under the redundant DOF

从图4和表1可以看出, 相对于无冗余轴的情况, 增加冗余轴C轴后, X轴和Y轴的运动量均有变化, XY合成运动量也发生了变化, 相应的合成轨迹与直线段的最大误差也不同.给定合适的C轴转角, 可以获取预期的X或Y轴的运动量.例如, 在实际加工中, 如果X轴的惯量较大, 运动冲击较大, 则可以取较大的C轴转角, 例如5° 、10° 或者15° , 以减小X轴的运动量, 使X轴的运动趋于平稳.虽然Y轴的运动量增大, 但X、Y平移轴的合成运动量在减小.类似地, 可以对Y轴的运动进行分解.

本文所提出的算法已经用于我们与福州某企业共同研发的某复杂曲面五坐标数控加工专机编程中.在传统的三轴数控加工中, 机床运动轴有X、Z和C轴, 其中X轴质量130 kg, 加工中运动量大, 决定着机床整体的最大进给速度.进给速度以C轴旋转运动表示, 最高可达28 800° /min.由于加工工艺的升级需求, 在研发的五轴数控机床中, 机床运动轴有X、Y、Z、B和C轴, 其中X轴质量增加到250 kg, 但由于增加了Y轴冗余自由度, 分解了X轴的运动, 最大进给速度仍然可以达到28 800° /min, 没有因为X轴的质量增加降低进给速度, 且此时机床运动冲击在可承受范围内.

4 结论

本文针对高速进给数控加工中, 运动轴可能存在的冲击问题进行了研究, 得出了以下结论.

1)对于确定的加工轨迹, 增加机床冗余自由度轴, 机床各轴的运动分量不再唯一, 对机床冲击较大轴的运动进行调整, 可减小运动冲击.

2)在冗余自由度下, 给出了机床运动轴的运动分解原理、加工合成轨迹算法, 以及增加冗余轴引起的加工轨迹误差计算方法.

理论分析和算例结果表明, 冗余自由度轴的增加对机床运动轴的运动量有分解作用, 能够有效减小机床运动冲击, 这为数控加工中进给速度的提高提供了可能性.

The authors have declared that no competing interests exist.

参考文献
[1] 章永年, 赵东标, 陆永华, 等. 平底刀最优刀轴矢量规划算法[J]. 机械工程学报, 2012, 48(5): 180-186.
ZHANG Yongnian, ZHAO Dongbiao, LU Yonghua, et al. Optimal tool orientation for five-axis flat-end cutter machining[J]. Journal of Mechanical Engineering, 2012, 48(5): 180-186. (in Chinese) [本文引用:1]
[2] 陈金成, 徐志明, 钟廷修, 等. 机床沿曲线高速加工时的运动学与动力学特性分析[J]. 机械工程学报, 2002, 38(1): 31-34.
CHEN Jincheng, XU Zhiming, ZHONG Tingxiu, et al. Kinematics and dynamics analysis of machine tool along the curves of high-speed machining[J]. Journal of Mechanical Engineering, 2002, 38(1): 31-34. (in Chinese) [本文引用:1]
[3] HO M C, HWANG Y R. A new decision algorithm of maximum allowable step length for 5-axis table-tilting type machining[J]. Journal of the Chinese Institute of Engineers, 2002, 25(2): 233-242. [本文引用:1]
[4] HU Pengcheng, TANG Kai. Improving the dynamics of five-axis machining through optimization of work-piece setup and tool orientations[J]. Computer-Aided Design, 2011, 43(12): 1693-1706. [本文引用:1]
[5] 罗明, 吴宝海, 李山, 等. 自由曲面五轴加工刀轴矢量的运动学优化方法[J]. 机械工程学报, 2009, 45(9): 158-163.
LUO Ming, WU Baohai, LI Shan, et al. Five-axis tool orientation optimization based on kinematical method[J]. Journal of Mechanical Engineering, 2009, 45(9): 158-163. (in Chinese) [本文引用:1]
[6] HO M C, HWANG Y R, HU C H. Five-axis tool orientation smoothing using quaternion interpolation algorithm[J]. International Journal of Machine Tools and Manufacture, 2003, 43(12): 1259-1267. [本文引用:1]
[7] BROOMHEAD P, EDKINS M. Generating NC data at the machine tool for the manufacture of free-form surfaces[J]. International Journal of Production Research, 1985: 24(1): 1-14. [本文引用:1]
[8] JUN C S, CHA K, LEE Y S. Optimizing tool orientations for 5-axis machining by configuration- space search method[J]. Computer-Aided Design, 2003, 35(6): 549-566. [本文引用:1]
[9] 毕庆贞, 王宇晗, 朱利民, 等. 刀触点网格上整体光顺五轴数控加工刀轴方向的模型与算法[J]. 中国科学, 2010, 40(10): 1159-1168.
BI Qingzhen, WANG Yuhan, ZHU Limin, et al. The model and algorithm of overall fairing five-axis NC machining tool axis direction on the cutter contact grid[J]. Science China Press, 2010, 40(10): 1159-1168. (in Chinese) [本文引用:1]
[10] 张立强, 王克用, 王宇晗. 复杂曲面五轴侧铣加工的运动学优化方法[J]. 中国机械工程, 2011, 22(21): 2589-2593.
ZHANG Liqiang, WANG Keyong, WANG Yuhan. Kinematical optimum method for five-axis flank milling complex surfaces[J]. China Mechanical Engineering, 2011, 22(21): 2589-2593. (in Chinese) [本文引用:1]
[11] WANG N, TANG K. Automatic generation of gouge-free and angular-velocity-compliant five axis tool path[J]. Computer-Aided Design, 2007, 39(10): 841-852. [本文引用:1]