引用本文
沈宇鹏, 张尧禹, 柴树山, 魏庆朝, 陈敦昌, 倪永军. 公路路桥过渡段搭板设计参数优化[J]. 北京交通大学学报, 2017,41(3): 55-60.
SHEN Yupeng, ZHANG Yaoyu, CHAI Shushan, WEI Qingchao, CHEN Dunchang, NI Yongjun. Optimization for design parameters of highway bridge approach slab[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2017,41(3): 55-60.
Doi:10.11860/j.issn.1673-0291.2017.03.009  
Permissions
版权所有 © 2017 《北京交通大学学报》编辑部
公路路桥过渡段搭板设计参数优化
沈宇鹏1, 张尧禹2, 柴树山1, 魏庆朝1, 陈敦昌1, 倪永军1
1.北京交通大学 土木建筑工程学院,北京 100044
2.中交公路规划设计院有限公司,北京 100088

第一作者:沈宇鹏(1977—),男,浙江嵊州人,副教授,博士.研究方向为路基工程.email: ypshen@bjtu.edu.cn.

收稿日期: 2016-11-21
基金: 交通运输部交通运输建设科技项目(2013318J06200); 中央高校基本科研业务费专项资金(2015JBM064); 教育部留学回国人员科研启动基金(第49批)
摘要

以车轮动荷载系数、桥面与引道路面容许台阶高度作为控制指标,建立七自由度车辆模型和过渡段三维动力学模型,分析桥头搭板的不同参数组合下车辆和过渡段的动力特性,提出搭板的优化设计参数,包括搭板厚度、弹性模量、长度和埋深.结果表明,考虑错台时,板厚不小于30 cm,弹性模量不小于2.8×104 MPa,长度为8.3 m能够满足桥头轻微跳车的要求和B级路面的后轮动荷载系数标准;弹性模量为2.8×104 MPa,长度为8.3 m的条件下,板厚不小于45 cm时能够满足A级路面的后轮最大动荷载系数标准;不考虑错台时,板厚为30 cm,弹性模量为2.8×104 MPa,长度不小于8.3 m时能够满足B级路面的前、后轮动荷载系数标准;搭板的埋深对路基累积沉降的影响不显著.建议搭板材质选取C25,长度、厚度分别不小于8.3 m和30 cm,埋深不大于0.1 m,以满足车轮动荷载系数和桥头轻微跳车的要求.

关键词: 公路工程; 桥头搭板; 评价指标; 参数优化; 动载系数; 容许台阶高度
中图分类号:U416.02 文献标志码:A 文章编号:1673-0291(2017)03-0055-06
Optimization for design parameters of highway bridge approach slab
SHEN Yupeng1, ZHANG Yaoyu2, CHAI Shushan1, WEI Qingchao1, CHEN Dunchang1, NI Yongjun1
1.School of Civil Engineering,Beijing Jiaotong University,Beijing 100044,China
2.CCCC Highway Consultants Co., Ltd., Beijing 100088,China
Fund:Construction Science and Technology Project of Ministry of Transport(2013318J06200); Fundamental Research Funds for the Central Universities(2015JBM06); Scientific Research Foundation for the Returned Overseas Chinese Scholars of Ministry of Education of China(No.49)
Abstract

Two parameters are applied as control indicators,including the dynamic wheel load factor and the allowable step height between the bridge and the bridge approach. Besides, the vehicle model with seven degrees of freedom and the three-dimensional dynamic model of transition section are established to analyze the dynamic characteristics of vehicle and approach under different combinations of slab parameters. And the optimum design parameters of bridge approach slab are proposed, including thickness, elastic moduli, length and buried depth of the slab. The results show that when the faulting of slab ends is considered, if the thickness of the slab is no less than 30 cm, the elastic moduli is over 2.8×104MPa, and the length is 8.3 m, the slab can meet the requirements of a slight bump and reach the dynamic rear wheel load factor standard of the B class road. While the elastic moduli is 2.8×104MPa, the length is 8.3 m, and the thickness is no less than 45cm, the slab can meet the dynamic rear wheel load factor standard of the A class road. When overlooking the faulting, if the thickness of the slab is 30cm, the elastic moduli is 2.8×104MPa, and the length is no less than 8.3 m, the slab can meet the dynamic wheel load factor standard of the B class road. However, the buried depth of slab has little effect on the cumulative settlement of subgrade. In order to meet the dynamic wheel load factor standard and the requirements of a slight bump, we advise to choose C25 as the material of bridge approach slab and make sure that the thickness is over 0.3m, the length is no less than 8.3m, and the buried depth is no more than 0.1m.

Keyword: highway engineering; bridge approach slab; evaluation index; parameters optimization; dynamic load factor; allowable step height

路桥过渡段桥头跳车现象已经成为公路最常见的质量缺陷之一, 不但严重影响行车安全性和舒适性, 还影响公路的养护维修、使用寿命等[1].利用搭板来缓和过渡是预防和减轻桥头跳车的主要措施之一, 因此搭板受力特性的分析和设计参数的选取成为研究的关键[2].目前, 设计规范中没有专门针对搭板设计参数的条目[3], 所以各家设计院提出各自的设计参数.

国内外学者开展了搭板受力及设计参数的研究.陈鹏等[4]在考虑了搭板的几何尺寸、材料和枕梁等因素的基础上, 分析了轴载受力特征; 刘润星等[5]通过对桥头搭板的尺寸参数、埋置角度及配筋设计的研究, 给出了搭板设计参数相关参考值; Long等[6, 7, 8]进行了理论研究和实验测试, 得到了不同的行车速度下搭板的差异沉降与舒适性的对应关系.

但在目前的研究中, 关于车辆重复荷载作用下不同搭板参数对车辆、桥头搭板、路基的受力特性及累积沉降的影响仍不是很明确.另外, 许多公路部门对桥头搭板设计参数的取值还局限在定值上, 而不会根据工程条件的改变对设计参数进行动态调整, 对于许多工况也没有统一的标准和相应的规范细则.

本文作者分析了公路不同桥头搭板参数对车辆经过过渡段时车轮动荷载系数和路基累积沉降的影响, 优化了搭板的厚度、弹性模量和长度, 为公路路桥过渡段搭板参数的选取提供依据.

1 桥头搭板设计评价指标及控制标准

在过渡段, 常用的车辆行驶平顺性指标包括车轮动荷载系数和桥面与引道路面容许台阶高度[9, 10, 11, 12].

1)车轮动荷载系数:动荷载评价指标是确定车辆动荷载的量化准则, 是理论分析和试验分析的前提, 动荷载系数越大证明车辆在道路上行驶时振动越剧烈, 行车越危险.

2)桥面与引道路面容许台阶高度:当发生局部沉陷或横坡变化时, 桥面与引道路面间发生垂直错台, 台阶高度决定行车舒适性和安全性, 台阶越高, 行车越不舒适, 甚至导致车轮跳离地面引起行车事故.

在公路标准载荷下, 一般A级路面动载系数为1.12~1.19, B级路面动载系数为1.23~1.38, C级路面动载系数为1.48~1.76, D级路面动载系数为2.00~2.52[10].本文作者参考文献[6, 13]的研究成果, 将错台高度25 mm作为容许台阶高度, 认为差异沉降小于25 mm时则满足桥头轻微跳车的要求.

2 计算模型
2.1 模型建立

以双轴重载车辆为研究对象, 考虑车体的沉浮、点头和侧倾运动, 以及4个车轮的垂向振动, 建立七自由度车辆模型[14], 如图1所示.

图1 七自由度整车模型Fig.1 A full vehicle model with seven degrees of freedom

图1中, xw1、xw2、xw3、xw4分别为4个车轮的竖向位移; xb为车体竖向位移; θ 为车体的俯仰角; φ 为车体的侧倾角; 以上7个变量代表车辆模型的7个自由度.xB1、xB2、xB3、xB4分别为4个车轮处的路面沉降; xb1、xb2、xb3、xb4为车轮传递给车辆悬架的竖向位移.

选取重载车辆计算速度为72 km/h, 以解放CA1253P7K1L11T1型6× 4载货汽车为例[14], 七自由度整车模型的其余参数如表1所示.

表1 车辆模型参数 Tab.1 Parameters of the vehicle model

由道路的实际运营状况可知, 车辆对其所在车道产生的影响远大于相邻车道.对道路的实际调查发现, 道路的破坏主要发生在重载方向, 因此, 采用重载方向的一幅路面来计算.桥梁为3× 13 m简支梁桥, 搭板顶面与路面面层底面高程相同, 箱梁模型如图2所示, 桥台、路基模型如图3所示.

图2 过渡段箱梁网格模型Fig.2 Grid model of box girder in the transition section

图3 过渡段桥台模型Fig.3 Model of bridge abutment in the transition section

对于模型的边界条件, 土基底部完全固定, 其余各结构层x、z方向固定, 深度y方向不固定.对于桥梁结构, 箱梁下部的桥墩结构用竖向弹簧来代替, 各结构层材料均匀, 层与层之间连续.

2.2 模型验证

车辆后轴重为100 kN, 当车辆分别以5 km/h和70 km/h驶过过渡段时, 将计算得出的面层底部的纵向应变同文献[15]中的实测数据进行对比, 结果如图4所示.

图4 不同速度时面层底部动力响应的测试数据与计算数据对比Fig.4 Comparison chart of the subgrade bottom dynamic response under different speeds between field measured data and simulation result

由图4可以看出, 计算数据和实测数据比较吻合, 都表现为前后轮分别经过该路段时产生两个极值, 验证了本文建立的模型是正确的.

过渡段桥台模型各结构层物理力学参数如表2所示, 其中搭板长度中有0.3 m支撑在桥台上.

表2 过渡段桥台模型的各结构层物理力学参数 Tab.2 Physical and mechanical parameters of bridge abutment model in the transition section
3 桥头搭板设计参数优化

采用控制变量的方法研究搭板参数对车辆行驶平顺性的影响, 当研究单一变量时, 其他塔板参数及荷载条件取为定值:搭板厚度30 cm, 弹性模量2.8× 104MPa, 长度8.3 m, 埋深10 cm, 荷载作用次数400万次.其中, 研究搭板厚度和搭板弹性模量的影响时, 考虑了错台的影响; 研究搭板长度和搭板埋深的影响时, 由于无法确定错台位置或错台有无对结果影响可忽略, 因此不考虑错台的影响.

3.1 搭板厚度

采用Li等[16]提出的修正Power模型计算车辆循环荷载下路基累积塑性应变

εp=a(σd/σs)mNb(1)

式中:ε p为累积塑性应变; σ d为车辆荷载引起的动偏应力, kPa; σ s为土体的静破坏偏应力, kPa; N为累计荷载作用次数; a、m和b为材料参数, 本文a取0.6, m取2.2, b取0.13.

计算各结构层的累积塑形应变后, 利用分层总和法计算总累积塑性变形

D=∑i=1nεp, ihi(2)

式中:ε p, i为第i层的累积塑形应变; hi为第i层厚度; n为总的分层数.

搭板厚度分别取25、30、35、45 cm时, 计算得到板厚与路基累积沉降关系曲线, 见图5.

图5 板厚与路基累积沉降关系Fig.5 Correlation between slab thickness and accumulative settlement of subgrade

当板厚为30 cm时, 能够满足桥头错台高度小于25 mm的要求, 随着搭板厚度的继续增加, 路基的累积沉降减小, 但减小的幅度减弱.不同板厚下前、后轮动荷载时程曲线如图6~图7所示.为了更加清晰地展现不同板厚下动荷载系数变化较大处的取值, 时程曲线从车辆前轴距离搭板末端6 m处开始绘制.

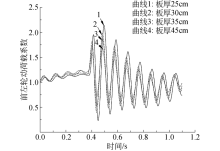图6 不同搭板厚度下前轮动荷载时程曲线Fig.6 Time-history curves of the front wheel dynamic load under different slab thicknesses

图7 不同搭板厚度下后轮动荷载时程曲线Fig.7 Time-history curves of the rear wheel dynamic load under different slab thicknesses

当板厚为30 cm时, 后轮最大动荷载系数为1.37, 已经能够满足B级路面的标准; 当板厚为45 cm时, 后轮最大动荷载系数为1.17, 可以满足A级路面的标准; 但是由于前轮胎的接触刚度比较小, 前轮的最大动荷载系数无法满足A、B级路面的标准.

3.2 搭板弹性模量

搭板弹性模量分别取2.2× 104 MPa、2.8× 104 MPa、3.0× 104 MPa、3.8× 104 MPa时, 计算得到搭板弹性模量与路基累积沉降关系, 见图8.其中, C25混凝土的弹性模量为2.8× 104 MPa, C30混凝土的弹性模量为3.0× 104 MPa, C80混凝土的弹性模量为3.8× 104 MPa.

图8 搭板弹性模量与路基累计沉降关系Fig.8 Correlation between slab elastic moduli and accumulative settlement of subgrade

当搭板弹性模量为2.8× 104 MPa时, 路基的累计沉降小于25 mm, 小于容许台阶高度, 满足桥头轻微跳车的要求.车辆前、后轮的动荷载系数时程曲线如图9~图10所示.为了更加清晰地展现不同弹性模量下动荷载系数变化较大处的取值, 时程曲线从车辆前轴距离搭板末端6 m处开始绘制.

图9 不同弹模下前轮动荷载系数时程曲线Fig.9 Time-history curves of the front wheel dynamic load under different slab elastic moduli

图10 不同弹模下后轮动荷载系数时程曲线Fig.10 Time-history curves of the rear wheel dynamic load under different slab elastic moduli

当搭板弹性模量为2.8× 104 MPa时, 后轮最大动荷载系数已经能够满足B级路面动荷载系数为1.23~1.38的标准; 但是前轮最大动荷载系数仍处于较大值.

3.3 搭板长度

搭板长度分别取6.3、8.3、10.3 m时, 计算得到不同搭板长度下车轮的前、后轮动荷载系数时程曲线, 见图11~图12.

图11 不同板长下车辆前轮动荷载系数时程曲线Fig.11 Time-history curves of the front wheel dynamic coefficient under different slab lengths

图12 不同板长下车辆后轮动荷载系数时程曲线Fig.12 Time-history curves of the real wheel dynamic coefficient under different slab lengths

由图11~图12可见, 当搭板长度为8.3 m时, 车辆前轮的最大动荷载系数为1.37, 满足B级路面动荷载系数的标准; 当搭板长度为6.3 m时, 车辆前轮的最大动荷载系数为1.46, 不满足B级路面动荷载系数的标准; 但是搭板长度的变化对前轮最小动荷载系数及后轮最大、最小动荷载系数的影响不显著.因此, 建议桥头搭板长度不小于8.3 m.

3.4 搭板埋深

搭板埋深分别取5、10、15、20 m时, 计算得到不同荷载作用次数下搭板埋深与路基累积沉降关系, 见图13.图13中路基的累积沉降随荷载作用次数的增大而增大; 在相同荷载作用次数下, 路基的累积沉降随搭板埋深而变化的幅度并不明显, 但从工程技术难度方面考虑, 推荐埋深不大于0.1 m.

图13 搭板埋深与路基累积沉降关系Fig.13 Correlation between slab buried depth and accumulative settlement of subgrade

4 结论

1)当搭板弹性模量为2.8× 104 MPa, 长度为8.3 m, 埋深为10 cm时, 从容许台阶高度方面考虑, 板厚不小于30 cm时能够满足桥头轻微跳车要求; 从后轮最大动荷载系数方面考虑, 板厚不小于45 cm时够满足A级路面标准.

2)当搭板厚度为30 cm, 长度为8.3 m, 埋深为10 cm时, 从容许台阶高度方面考虑, 搭板弹性模量不小于2.8× 104 MPa时能够满足桥头轻微跳车要求; 从后轮最大动荷载系数方面考虑, 搭板弹模不小于2.80× 104 MPa时能够满足B级路面的标准.

3)当搭板厚度为30 cm, 弹性模量为2.8× 104 MPa, 埋深为10 cm时, 从前、后轮动荷载系数方面考虑, 搭板长度不小于8.3 m时能够满足B级路面的标准.

4)当搭板厚度为30 cm, 弹性模量为2.8× 104 MPa, 长度为8.3 m时, 搭板的埋深对路基累积沉降的影响不是很明显, 且都能满足桥头轻微跳车和前、后轮动荷载系数的要求.

综上所述, 在工程实际中设计搭板的参数时, 应尽量结合道路建设的实际情况、施工的需要及工程造价等条件来综合取值.

The authors have declared that no competing interests exist.

参考文献
[1] 彭银辉. 公路桥头跳车病害处治技术研究[D]. 哈尔滨: 东北林业大学, 2010.
PENG Yinhui. Treatment technology research of vehicle dumping at bridgehead[D]. Harbin: Northeast Forestry University, 2010. (in Chinese) [本文引用:1]
[2] 乔华. 桥头搭板设计方法及技术参数的研究[D]. 西安: 长安大学, 2011.
QIAO Hua. Researches into the design approach and technical parameters of approach-slabs[D]. Xi’an: Chang’an University, 2011. (in Chinese) [本文引用:1]
[3] 公路路基设计规范: JTG D30—2004[S]. 北京: 人民交通出版社, 2004.
Code for design of highway subgrades: JTG D30—2004[S]. Beijing: China Communications Press, 2004. (in Chinese) [本文引用:1]
[4] 陈鹏, 郑传超. 路桥过渡段搭板受力分析[J]. 西安公路交通大学学报, 1998, 18(3): 244-251.
CHEN Peng, ZHENG Chuanchao. Structural analysis on the approach slabs between pavements and abutment[J]. Journal of Xi’an Highway University, 1998, 18(3): 244-251. (in Chinese) [本文引用:1]
[5] 刘润星, 王海亮. 桥头搭板设计方法与技术参数研究[J]. 内蒙古公路与运输, 2009(2): 15-17.
LIU Runxing, WANG Hailiang. Research on the design methods and technical parameters of bridge approach slabs[J]. Highways &Transportation in Inner Mongolia, 2009(2): 15-17. (in Chinese) [本文引用:1]
[6] LONG J, OLSON S, STARK T, et al. Differential movement at embankment-bridge structure interface in Illinois[J]. Transportation Research Record, 1998(1633): 53-60. [本文引用:2]
[7] THIELE D J, TADROS M K, BENAK J V. State of the art for control of bridge approach settlement[J]. Bridge Evaluation Repair and Rehabilitation, 1990, 187: 57-70. [本文引用:1]
[8] 冯忠居, 方贻立, 龚坚城, 等. 高等级公路桥头跳车的危害及其机理的分析[J]. 西安公路交通大学学报, 1999, 19(4): 33-35.
FENG Zhongju, FANG Yili, GONG Jiancheng, et al. Analysis of the harmful effect of vehicle bump at bridge-head of the highway and its mechanism[J]. Journal of Xi’an Highway University, 1999, 19(4): 33-35. (in Chinese) [本文引用:1]
[9] 王智德. 搭板设计参数优化解决桥头跳车的研究及应用[D]. 武汉: 武汉理工大学, 2011.
WANG Zhide. Research and application of slab’s design parameter optimization to solve bump at bridge head[D]. Wuhan : Wuhan University of Technology, 2011. (in Chinese) [本文引用:1]
[10] 董忠红, 吕彭民. 高等级路面上的车辆动载荷[J]. 长安大学学报(自然科学版), 2010, 30(1): 95-99.
DONG Zhonghong, LYU Pengmin. Dynamic load of vehicle on high-class pavement[J]. Journal of Chang’an University (Natural Science Edition), 2010, 30(1): 95-99. (in Chinese) [本文引用:2]
[11] 李献民, 王永和, 倪宏革, 等. 动力分散型机车在路涵过渡段的动应力-应变研究[J]. 岩土力学, 2004, 25(7): 1167-1170.
LI Xianmin, WANG Yonghe, NI Hongge, et al. Study on dynamic stress-strain in roadbed-culvert transition section for DIDLG[J]. Rock and Soil Mechanics, 2004, 25(7): 1167-1170. (in Chinese) [本文引用:1]
[12] 张洪亮, 胡长顺, 吕文江. 路桥过渡段容许差异沉降计算模型[J]. 交通运输工程学报, 2005, 5(1): 19-23.
ZHANG Hongliang, HU Changshun, LYU Wenjiang. Theoretical models of determining tolerable differential settlement at end of bridge[J]. Journal of Traffic and Transportation Engineering, 2005, 5(1): 19-23. (in Chinese) [本文引用:1]
[13] STARK T D, OLSON S M, LONG J H. Differential movement at the embankment/structure interface-mitigation and rehabilitation[R]. Springfield: Illinois, 1995. [本文引用:1]
[14] SHI X M, CAI C S. Simulation of dynamic effects of vehicles on pavement using a 3D interaction model[J]. Journal of Transportation Engineering, 2009, 135(10): 736-744. [本文引用:2]
[15] 董忠红, 吕彭民. 车辆-沥青路面系统力学分析[M]. 北京: 人民交通出版社, 2010: 129-130.
DONG Zhonghong, LYU Pengmin. Mechanical analysis of vehicle-asphalt pavement system[M]. Beijing: China Communications Press, 2010: 129-130. (in Chinese) [本文引用:1]
[16] LI D Q, SELIG E T. Cumulative plastic deformation for fine-grained subgrade soils[J]. Journal of Geotechnical Engineering, 1996, 122(12): 1006-1013. [本文引用:1]