疲劳裂纹扩展门槛值测试技术

引用本文

刘青峰, 张治国, 邹骅, 李晓阳. 疲劳裂纹扩展门槛值测试技术[J]. 北京交通大学学报, 2017,41(3): 109-113.
LIU Qingfeng, ZHANG Zhiguo, ZOU Hua, LI Xiaoyang. Measuring and testing techniques of fatigue crack growth threshold[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2017,41(3): 109-113.
Doi:10.11860/j.issn.1673-0291.2017.03.017 复制到剪切板

Permissions

疲劳裂纹扩展门槛值测试技术

刘青峰¹, 张治国², 邹骅³, 李晓阳⁴

1. 92117部队,北京 100072

2.中国铁道科学研究院标准计量研究所,北京 100081

3.北京交通大学机械与电子控制工程学院,北京 100044

4.北京工业大学机械工程与应用电子技术学院,北京 100022

第一作者:刘青峰(1972—),男,山东莱阳人,高级工程师,博士.研究方向为车辆结构疲劳可靠性.email:liuqingfeng72@163.com.

收稿日期: 2015-03-23

摘要

针对裂纹扩展门槛值测量技术中存在的不足,应用数字化测量技术采集试样测点位移与试验载荷,采用柔度法计算裂纹长度,由测点位移波形的峰值记录循环次数,多线程软件设计实现试验控制和数据采集、监视与处理一体化,从而保证测试结果的准确性.根据不同载荷比下40CrNiMo钢疲劳裂纹扩展门槛值成组试验的结果,验证了上述测试技术的可靠性与可行性.

关键词: 裂纹测试技术; 柔度法; 应力强度因子; 疲劳裂纹扩展门槛值

中图分类号:U270.12 文献标志码:A 文章编号:1673-0291(2017)03-0109-05

Measuring and testing techniques of fatigue crack growth threshold

LIU Qingfeng¹, ZHANG Zhiguo², ZOU Hua³, LI Xiaoyang⁴

1. 92117 Troops, Beijing 100072,China

2. Standards & Metrology Research Institute, China Academy of Railway Sciences, Beijing 100081,China;

3. School of Mechanical, Electronic and Control Engineering, Beijing Jiaotong University, Beijing 100044,China

4. College of Mechanical Engineering and Applied Electronics Technology,Beijing University of Technology, Beijing 100022,China

Abstract

In view of insufficiency in crack growth threshold measurement technology, the survey-point displacement of specimen and test-load are collected through digital measurement technology, and the crack size is calculated through the compliance method, the cycle index is recorded according to the wave crest of survey-point displacement. Besides, the integrated objective of test control, data collection, monitoring and processing are implemented by the multi-thread software. The results of the fatigue crack growth thresholds of steel 40CrNiMo, which are obtained from group test method under different load-ratio, prove the reliability and feasibility of measuring and testing techniques.

Keyword: crack testing technology; compliance method; stress intensity factor; fatigue crack growth threshold

文章图片

服役工程结构的疲劳破坏通常是由于疲劳裂纹扩展造成的, 疲劳裂纹扩展是疲劳设计的重要研究内容, 材料疲劳裂纹扩展门槛值对于结构疲劳设计尤为重要^[1].为准确获得材料的疲劳裂纹扩展门槛值, 需要在试验中实时采集和同步显示裂纹长度、循环次数和试验载荷^[2], 从而导致试验数据采集量大,

传统的测试技术不能满足试验要求.目前裂纹长度测试方法有很多种, 如目测法、柔度法^[3]、电位法^[4]、图像法^[5]等, 其中目测法劳动强度大、精度差, 特别是当测量点较少时, 试验结果会受到影响; 电位法不需要观察裂纹, 测量工作量小, 但电位差测试仪器精度要求高, 影响因素较多, 获得的数据结果有时不太稳定; 图像法是较新的裂纹长度测试技术, 基于CCD图像处理获得裂纹长度, 对于裂纹尖端的锐化与钝化的循环、裂纹扩展的连续与微跳的增长, 图像法具有一定的优势, 但该方法对测试仪器要求较高; 柔度法容易实现数据的连续采集与实时同步, 具有较高的测量精度, 且操作简便, 应用广泛^{[6, 7, 8]}.为此, 本文基于柔度法进行裂纹长度的测试和计算中, 采用多线程的软件结构, 将测试任务分成几个并行运行、完成不同功能的线程, 实现试验控制和数据采集、监视与处理一体化.

1 理论背景

1.1 裂纹扩展理论

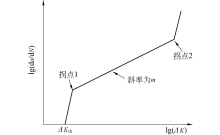
裂纹扩展是裂纹由初始尺寸扩展到临界尺寸的过程.裂纹扩展速率 $d a / d N$ 和应力强度因子范围 $ΔK$ 的关系采用Paris公式可写为^[10]

$d a / d N = C {(ΔK)}^{m} (1)$

式中: $C$ 、 $m$ 为与材料和试验条件有关的参数; $a$ 为裂纹长度, mm; $N$ 为载荷循环次数, cycle.

理论上 $ΔK$ 与 $d a / d N$ 的关系采用双对数曲线表示, 如图1所示.当裂纹尖端的应力强度因子范围 $ΔK$ 小于裂纹扩展门槛值 $Δ K_{th}$ (一般取 $d a / d N$ =10^-7mm/cycle对应的 $ΔK$ 值)时, 裂纹不发生扩展; 当 $ΔK$ 超过 $Δ K_{th}$ 后, 裂纹开始扩展, 随着裂纹长度的增加, 裂纹进入稳定扩展区, 即拐点1和拐点2对应的区间; 当裂纹长度扩展超过拐点2后, 裂纹快速扩展至断裂.

	Figure Option View Download New Window
	图1 lg(da/dN)-lg△ K曲线Fig.1 Curve of $\lg (d a / d N) - \lg △ K$

1.2 柔度法原理

柔度用来表征构件抵抗变形的能力, 当构件中裂纹萌生或扩展, 构件柔度也会随着其抵抗变形的能力而相应变化.在其它条件不变时, 柔度的变化可用来监测裂纹的变化.高同步性与线性度的载荷、位移信号和高速数据采集与处理组件是柔度法准确测试裂纹长度的保证.

CT试样柔度与裂纹长度的关系用柔度(EV_XB)/P和归一化裂纹长度a/W表达为^[9]

$a / W = (C_{0} + C_{1} U_{X} + C_{2} U_{X}^{2} + \dots + C_{5} U_{X}^{5}) (2)$

式中: C₀ 、C₁ 、…、C₅ 为柔度系数; W为加载线到试样远端的距离; U_X为柔度表达式, 即

$U_{X} = [(E V_{X} {B / P)}^{1 / 2} {+ 1]}^{- 1} (3)$

式中: B为试样厚度; E为弹性模量; V_X 为试样测点X的位移; P为静载荷.

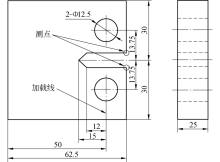
图2为试样位移测点位置示意图, 试样测点位置对应的柔度系数值 $C_{0} ~ C_{5}$ 分别为:1.001、-4.669 5、18.46、-236.82、1 214.9与-2 143.6^[9].

	Figure Option View Download New Window
	图2 CT试样位移测点位置(单位:mm)Fig.2 Measuring point position of CT specimen(unit:mm)

2 系统设计

2.1 硬件设计

测点位移采集硬件系统由引伸计、桥源、放大器、A/D板、抑零漂电路和计算机组成^[11].选用INSTRON高频引伸计, 见图3, 其能在不大于500 Hz的试验频域下正常工作, 裂纹长度测量精度达到0.5 μ m.A/D板的采集速度和精度决定了系统的采样速度和精度, 系统所用A/D板的分辨率为1/4 096, 采集频率大于2 kHz.在高频疲劳试验机载荷标定系统的基础上, 通过I/O板直接采集记录载荷值.

	Figure Option View Download New Window
	图3 INSTRON高频引伸计Fig.3 INSTRON high frequency extensometer

2.2 软件设计

Windows操作系统可同时运行多个进程(程序实例), 每个进程可同时运行多个线程(子任务), 所有线程可访问进程的全部资源和变量, 易实现线程间的通信, 即一个线程生成的数据可立即提供给其他线程.多线程程序可以同时完成不同的工作, 使得结构既可提高CPU的利用率和程序的响应、运行速度, 又可减少系统的等待时间和资源浪费, 这样程序采样的速度快、可靠性高.

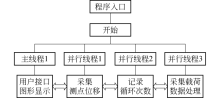
软件系统采用VC++编程, 系统多线程程序结构见图4.主线程用于用户接口, 作用是响应用户事件, 并显示图形与数据; 线程1用于采集测点位移, 线程2用于记录循环次数, 由于数据量大、频率高, 所以设定线程1和线程2拥有较高的优先级; 线程3用于采集载荷和数据处理, 鉴于频繁存盘消耗大量系统资源, 会使采集测点位移和循环次数滞后, 因此程序设计时, 先把数据存储到缓存, 停止采集时再存盘, 即进行数据的分步存盘.

	Figure Option View Download New Window
	图4 多线程程序结构Fig.4 Multithread program structure

3 数据测试与处理

3.1 数据测试

3.1.1 裂纹扩展长度

通过INSTRON高频引伸计测试试样测点位移, 然后通过柔度法计算裂纹长度.

1)测点位移数据格式.

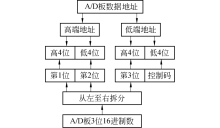
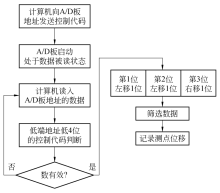
A/D板的地址、数据及数据存放的格式见图5, 将3位16进制数从左至右拆分并移位:第1位、第2位分别右移1位, 存放到高端地址的高4位和低4位; 第3位左移1位存放到低端地址的高4位, 低4位存放数据有效性控制码.

	Figure Option View Download New Window
	图5 地址和数据格式Fig.5 Address and data format

2)测点位移的采集协议.

计算机与A/D板的通信流程见图6.A/D板收到控制码, 进行模数转换, 处于数据被读状态, 计算机读入A/D板地址里的数据, 存放在低端地址低4位的控制码用于数据的有效性校验, 数据无效, 计算机重新读; 数据有效, 进行数据还原, 存放在高端地址高4位和低4位的数(第1位、第2位)左移1位, 存放在低端地址高4位数(第3位)右移1位, 记录下测点位移信息.

	Figure Option View Download New Window
	图6 通信协议Fig.6 Communications protocol

3)采样频率分析.

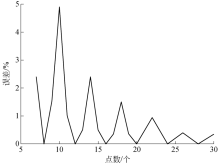
对于通常70~170 Hz的高频试验, 在每个循环中, 系统可采集至少11个点信息, 采样间隔相等, 但采集点数是变化的.通过等幅正弦波采样将每个循环采集的极值来替代其真实的极值造成的误差, 其与采集点数的关系曲线见图7, 假设循环只采集了10个点, 误差小于5%.每个循环采集的点数不小于11个, 误差在2%左右, 如果频率在100 Hz左右, 每个循环可采集20个点, 误差仅在1%左右, 测点位移的测试具有较高的精度, 通过测点位移均值计算的裂纹扩展长度同样具有较高的精度.

	Figure Option View Download New Window
	图7 采集点数与误差曲线Fig.7 Curve between acquisition point number and the error

3.1.2 循环计数

试样承受等幅正弦波循环载荷, 其测点同步产生循环位移.由采集测点位移线程记录的全部位移信息, 通过记录循环次数线程统计位移波形的峰值, 由峰值法记录循环次数^[12].测点位移的高精度测试有效保证了循环计数的高精度.

3.1.3 试验载荷

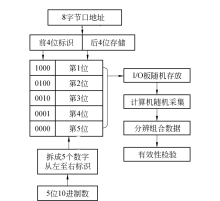
	Figure Option View Download New Window
	图8 载荷采集协议Fig.8 Loading acquisition protocols

100 kN的试验系统的载荷采集协议见图8, 精度是0.01 kN, 将5位10进制数, 从左至右拆分并给5位数标识1000、0100、0010、0001和0000, 等于给这5位数分别多加了128、64、32、16和0, 标识与相应的载荷数值分别存放在I/O板口地址的前4位和后4位, I/O板随机存放一组标识和数, 计算机采集并分辨这5位数, 有效性校验后, 组合方法为:(第1位-128)× 100+(第2位-64)× 10+(第3位-32)× 1+(第4位-16)/10+(第5位-0)/100.

有效采集的载荷不能超出系统的量程100 kN.第1位只能等于0或1, 否则无效.第1位等于0, 数据有效.第1位等于1且其余位等于0, 数据有效; 第1位数等于1且其余位不都等于0, 数据无效.试验载荷的约定采集协议, 优化了采样的有效性.

3.2 数据处理

数据处理是通过软件的数据处理模块实现的, 处理流程如下:

1)设定j个循环算一次测点位移, j为奇数, 取值可从1到几百, 共进行了k次测试, 第i次测试的测点位移均值为V_i, 根据式(2)计算裂纹长度, 得到第i次测试的裂纹长度a_i 和循环次数N_i.第i次测试的测点位移均值V_i为

$V_{i} = \frac{\overset{j}{\sum_{i = 1}} (V_{i \max} + V_{i \min})_{i}}{2 j} (4)$

式中: $V_{i \max}$ 、 $V_{i \min}$ 分别为第i个循环中位移的最大值和最小值.

2)用递增多项式局部拟合求导, 确定裂纹扩展速率和裂纹长度拟合值^[9].取 $(a_{i}, N_{i})$ 数据点前面和后面各 $n$ 个点, 共2n+1个连续点, n值可取2、3、4.采用二次多项式拟合求导:

${\dot{a}}_{i} = b_{0} + b_{1} (\frac{N_{i} - f_{1}}{f_{2}}) + b_{2} {(\frac{N_{i} - f_{1}}{f_{2}})}^{2} (5)$

$\begin{matrix} \{\begin{array}{l} - 1 \leq \frac{N_{i} - f_{1}}{f_{2}} \leq 1 \\ f_{1} = \frac{1}{2} (N_{i - n} + N_{i + n}) \\ f_{2} = \frac{1}{2} (N_{i + n} - N_{i - n}) \\ a_{i - n} \leq a \leq a_{i + n} \end{array} (6) \end{matrix}$

式中:系数 $b_{0}$ 、 $b_{1}$ 、 $b_{2}$ 是按最小二乘法确定的拟合参数; ${\dot{a}}_{i}$ 是对应于循环次数 $N_{i}$ 的拟合裂纹长度; 参数 $f_{1}$ 、 $f_{2}$ 用于变换输入数据.

在 $N_{i}$ 处的裂纹扩展速率 ${(d a / d N)}_{{\dot{a}}_{i}}$ 由式(5)求导获得:

${(\frac{d a}{d N})}_{{\dot{a}}_{i}} = \frac{b_{1}}{f_{2}} + \frac{2 b_{2} (N_{i} - f_{1})}{f_{2}} (7)$

3)CT试样 $ΔK$ 的计算表达式为^[9]

$\begin{array}{l} ΔK = \frac{ΔP}{B \sqrt[]{W}} \times \frac{(2 + α)}{{(1 - α)}^{3 / 2}} \times (0.886 + 4.64 α - \\ 13.32 α^{2} + 14.72 α^{3} - 5.6 α^{4}) (8) \end{array}$

式中: $α$ 为归一化裂纹长度, $α = a / W$ ; $ΔP$ 为载荷变程, 为动载荷 $P_{d}$ 的2倍, 即 $ΔP = 2 P_{d}$ .

将 ${(d a / d N)}_{i}$ 对应的动载荷 ${(P_{d})}_{i}$ 代入式(8), 从而得到第 $i$ 次循环中的裂纹应力强度因子 $Δ K_{i}$ .

4)由 $({(d a / d N)}_{i}, Δ K_{i})$ 数据的关系曲线, 确定近门槛扩展区的拐点, 采用最小二乘法分别拟合稳定扩展与近门槛扩展区数据, 获得Paris公式参数 $C$ 、 $m$ 和裂纹扩展门槛值 $Δ K_{th}$ .

4 试验设计与结果分析

采用抚顺钢厂冶炼的40 CrNiMo钢的30个CT试样, 进行载荷比为0.1、0.3和0.5的3组试验, 每组10个试样, 测得的结果如表1所示.

表1 试验结果 Tab.1 Test results

载荷比	$Δ K_{th}$ 均值	$Δ K_{th}$ 均方差	$m$ 均值	$m$ 均方差	$C$ 均值	$C$ 均方差
0.1	6.64	0.36	3.82	0.25	3.20× 10^-15	2.58× 10^-15
0.3	5.66	0.30	3.78	0.20	3.66× 10^-15	2.12× 10^-15
0.5	3.86	0.33	3.73	0.22	1.43× 10^-14	1.33× 10^-14

表1 试验结果 Tab.1 Test results

从试验结果看, 40 CrNiMo钢裂纹扩展门槛值 $Δ K_{th}$ 随试验载荷比的增大而减小, 对应每组中的10个试件算得裂纹扩展门槛值 $Δ K_{th}$ 平均值的均方差分别为0.36、0.30和0.33, 均方差的数值较小, 能反映材料40 CrNiMo钢的疲劳裂纹扩展门槛值 $Δ K_{th}$ .

在不同的载荷比下, 40 CrNiMo钢疲劳裂纹稳定扩展阶参数 $m$ 的平均值相当接近, 分别为3.82、3.78和3.73, 符合 $m$ 不随构件的形状和载荷性质而改变, 多数金属材料的 $m$ 值在2~4的范围内的规律.对应每组中的10个试件算得参数 $m$ 平均值的均方差分别为0.25、0.20和0.22, 均方差较小, 说明试验系统具有较高的稳定性.

在不同的载荷比下, 40 CrNiMo钢疲劳裂纹稳定扩展阶段参数 $C$ 的平均值分别为3.20e-15、3.66e-15和1.43e-14, 对应每组中的10个试件算得参数 $C$ 的平均值的均方差分别为2.58e-15、2.12e-15和1.33e-14, 参数C的计算结果分散性相对较大, 也符合参数C与材料的力学性能、试验条件等有关的情况.

5 结论

1)基于100 kN高频疲劳试验机组建了一套测定疲劳裂纹扩展速率及其门槛值的自动化测试系统, 实现了试验控制和数据采集、监视与处理一体化, 由成组试验验证了测试系统具有较高的精度和稳定性, 为疲劳试验系统的发展完善提供了新思路和方法.

2)采用柔度法由测点位移均值计算裂纹扩展长度, 由测点位移波形的峰值记录循环次数, 试验载荷实时数字化测量, 多线程软件设计实现试验控制和数据采集、监视与处理一体化, 提高了测试效率和精度.

3)由试验测得了40 CrNiMo钢的疲劳裂纹扩展门槛值, 为疲劳设计提供了依据.

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	高镇同. 疲劳应用统计学[M]. 北京: 国防工业出版社, 1986: 191-198. GAO Zhentong. Applied statistics in fatigue[M]. Beijing: National Defense Industry Press, 1986: 191-198. (in Chinese) [本文引用:1]
[2]	SAXENA A, HUDAK S. Review and extension of compliance information for common crack growth specimens[J]. International Journal of Fracture, 1978, 14(5): 453-468. [本文引用:1]
[3]	张利娟, 张亚军, 高灵清. 表面裂纹长度的测量方法[J]. 材料开发与应用, 2009, 24(5): 75-78. ZHANG Lijuan, ZHANG Yajun, GAO Lingqing. Review on measurement methods of surface crack length[J]. Exploitation and Application of Material, 2009, 24(5): 75-78. (in Chinese) [本文引用:1]
[4]	SCHWALBE K H, HELLMANN D. Application of the electrical potential method to crack length measurements using Johnson’s formula[J]. JTEVA, 1981, 9(3): 218-221. [本文引用:1]
[5]	KANCHANOMAI C, YAMAMOTO S, MIYASHITA Y. High cycle fatigue test for solders using non-contact digital image measurement system[J]. International Journal of Fatigue, 2002, 24(1): 57-67. [本文引用:1]
[6]	张旦闻, 刘宏昭, 刘平. 裂纹柔度法在7075铝合金板残余应力检测中的应用[J]. 材料热处理学报, 2006, 27(2): 127-131. ZHANG Danwen, LIU Hongzhao, LIU Ping. Application of residual stress measurement on 7075 Aluminum Alloy plate based on the cracking flexibility method[J]. Transactions of Materials and Heat Treatment, 2006, 27(2): 127-131. (in Chinese) [本文引用:1]
[7]	伍光胜, 宋信忠, 郑明辉. 多线程技术及其应用的研究[J]. 计算机应用研究, 2001, 18(1): 33-36. WU Guangsheng, SONG Xinzhong, ZHENG Minghui. Study and application of multithread technology[J]. Application Research of Computers, 2001, 18(1): 33-36. (in Chinese) [本文引用:1]
[8]	刘青峰. 疲劳裂纹扩展速率与门槛值自动化测试系统研究[D]. 北京: 北京工业大学, 2000. LIU Qingfeng. Automation test system research of fatigue crack growth rate and the threshold value[D]. Beijing: Beijing University of Technology, 2000. (in Chinese) [本文引用:1]
[9]	PARIS P C, ERDOGAN F. A critical analysis of crack propagation laws[J]. Journal of Basic Engineering, 1963, 85(4): 528-534. [本文引用:4]
[10]	ASTM Committee on Stand ards. Stand ard test method for measurement of fatigue crack growth rates: E647-2000[S]. Philadelphia: American Society for Testing and Materials, 2001. [本文引用:1]
[11]	汤晓华, 刘九庆, 陈强, 等. 低周疲劳裂纹扩展速率的试验系统[J]. 东北林业大学学报, 2006, 34(1): 78-80. TANG Xiaohua, LIU Jiuqing, CHEN Qiang, et al. Test system of low-cycle fatigue crack growth rate[J]. Journal of Northeast Forestry University, 2006, 34(1): 78-80. (in Chinese) [本文引用:1]
[12]	高镇同, 蒋新桐, 熊峻江, 等. 疲劳性能试验设计和数据处理[M]. 北京: 北京航空航天出版社, 1999: 6-20. GAO Zhentong, JIANG Xintong, XIONG Junjiang, et al. Experiment design and data processing of fatigue[M]. Beijing: Beijing Aerospace Press, 1999: 6-20. (in Chinese) [本文引用:1]

1986

0.0

... 服役工程结构的疲劳破坏通常是由于疲劳裂纹扩展造成的,疲劳裂纹扩展是疲劳设计的重要研究内容,材料疲劳裂纹扩展门槛值对于结构疲劳设计尤为重要^[1] ...

1978

0.0

... 为准确获得材料的疲劳裂纹扩展门槛值,需要在试验中实时采集和同步显示裂纹长度、循环次数和试验载荷^[2],从而导致试验数据采集量大, ...

2009

0.0

张利娟, 张亚军, 高灵清. 表面裂纹长度的测量方法[J]. 材料开发与应用, 2009, 24(5): 75-78.

ZHANG

Lijuan

, ZHANG

Yajun

, GAO

Lingqing

. Review on measurement methods of surface crack length[J]. Exploitation and Application of Material, 2009, 24(5): 75-78. (in Chinese)

表面裂纹长度的精确测量是准确获得表面裂纹扩展速率进而对材料或构件进行剩余寿命评估的基础和关键技术问题.本文将表面裂纹长度的测量方法归类为直读法、柔度法、电位法、探伤法和光学法,并对每种方法进行了介绍,比较其优缺点及适用范围,以便在实际工作中选择应用.

... 目前裂纹长度测试方法有很多种,如目测法、柔度法^[3]、电位法^[4]、图像法^[5]等,其中目测法劳动强度大、精度差,特别是当测量点较少时,试验结果会受到影响 ...

1981

0.0

2002

0.0

2006

0.0

张旦闻, 刘宏昭, 刘平. 裂纹柔度法在7075铝合金板残余应力检测中的应用[J]. 材料热处理学报, 2006, 27(2): 127-131.

ZHANG

Danwen

, LIU

Hongzhao

, LIU

Ping

. Application of residual stress measurement on 7075 Aluminum Alloy plate based on the cracking flexibility method[J]. Transactions of Materials and Heat Treatment, 2006, 27(2): 127-131. (in Chinese)

运用裂纹柔度法检测了7075-T73、T7351、T7352铝合金板中的残余应力.试验发现:应变测量误差主要源自在试验后期试样重力的影响以局部温度变化的影响.在裂纹柔度法计算中引入权函数能有效的抑制测量误差,提高残余应力检测精度.用梁弯曲试验对裂纹柔度法试验结果作了验证,提出了权函数参数(t1,t2)的设置方法,试验结果与理论值取得良好一致.试验结果表明:铝合金板的预拉伸工艺可消除约90%的残余应力.压缩工艺可获得压缩的残余应力,对应力消除的效果最佳.

... 柔度法容易实现数据的连续采集与实时同步,具有较高的测量精度,且操作简便,应用广泛^[6,7,8] ...

2001

0.0

伍光胜, 宋信忠, 郑明辉. 多线程技术及其应用的研究[J]. 计算机应用研究, 2001, 18(1): 33-36.

Guangsheng

, SONG

Xinzhong

, ZHENG

Minghui

. Study and application of multithread technology[J]. Application Research of Computers, 2001, 18(1): 33-36. (in Chinese)

多线程是目前多种操作系统支持的主要技术之一，其对改进程序的结构及提高计算机的性能起很大的作用。基于Windows NT操作系统进行分析、讨论，并以复合通信作为其应用的例子，给出解决问题的方法。

... 柔度法容易实现数据的连续采集与实时同步,具有较高的测量精度,且操作简便,应用广泛^[6,7,8] ...

2000

0.0

刘青峰. 疲劳裂纹扩展速率与门槛值自动化测试系统研究[D]. 北京: 北京工业大学, 2000.

LIU

Qingfeng

. Automation test system research of fatigue crack growth rate and the threshold value[D]. Beijing: Beijing University of Technology, 2000. (in Chinese)

本文根据国标（GB 6398—86）中的金属材料疲劳裂纹扩展速率试验方法及其附录C——金属材料疲劳裂纹扩展门槛值试验方法，以疲劳裂纹扩展理论为基础，结合成熟的数字化采集技术，进行了疲劳裂纹扩展速率和门槛值自动化测试系统及试验技术的研究。本文研究开发了一套金属材料疲劳裂纹扩展速率和门槛值自动化测试试验系统，系统包括精度高、稳定性好的数据采集硬件系统，功能强大、操作简单的数据处理软件系统，并且利用该测试系统进行了40CrNiMo钢疲劳裂纹扩展速率和门槛值的试验研究，获得了40CrNiMo钢疲劳性能试验数据，通过试验验证了该测试系统的稳定性和精度完全符合国标的要求；试验中主要研究了循环次数的记录、零漂的跟踪补偿、裂纹扩展尺寸的计算和加载比的控制等重要的试验技术；该测试系统提供了一套老式疲劳试验机改造的新方案，具有造价便宜，实用价值高，较为先进的特点，值得推广应用。

... 柔度法容易实现数据的连续采集与实时同步,具有较高的测量精度,且操作简便,应用广泛^[6,7,8] ...

1963

0.0

... CT试样柔度与裂纹长度的关系用柔度(EV_XB)/P和归一化裂纹长度a/W表达为^[9] ...

... 6^[9] ...

... 2)用递增多项式局部拟合求导,确定裂纹扩展速率和裂纹长度拟合值^[9] ...

... 3)CT试样 ΔK的计算表达式为^[9] ...

2001

0.0

... 裂纹扩展速率 da/dN和应力强度因子范围 ΔK的关系采用Paris公式可写为^[10] ...

2006

0.0

汤晓华, 刘九庆, 陈强, 等. 低周疲劳裂纹扩展速率的试验系统[J]. 东北林业大学学报, 2006, 34(1): 78-80.

TANG

Xiaohua

, LIU

Jiuqing

, CHEN

Qiang

, et al. Test system of low-cycle fatigue crack growth rate[J]. Journal of Northeast Forestry University, 2006, 34(1): 78-80. (in Chinese)

结合Instron 1343疲劳试验机开发了低周疲劳裂纹扩展速率试验系统.系统由数据采集和计算机数据处理软件两部分组成,可以在连续、停机状态下完成常温、低温(-50℃)实时采集载荷P、载荷位移D和裂纹缺口位移1/3个模拟量数据采集.在制动盘蠕墨铸铁常温、低温(-50℃)低周疲劳裂纹扩展速率试验中得到应用.

... 1 硬件设计测点位移采集硬件系统由引伸计、桥源、放大器、A/D板、抑零漂电路和计算机组成^[11] ...

1999

0.0

... 由采集测点位移线程记录的全部位移信息,通过记录循环次数线程统计位移波形的峰值,由峰值法记录循环次数^[12] ...