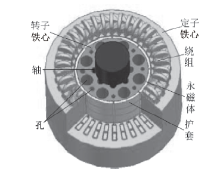
本文以一台伺服永磁同步电动机为研究对象, 样机的额定功率为12.5 kW, 额定电压为364 V, 额定转速为2 000 r/min, 额定频率为133.33 Hz.电机转子铁心采用局部空心结构, 转子永磁体采用表贴式结构, 在永磁体外加一护套, 主要用于固定和保护永磁体, 防止运行时永磁体脱落.护套采用轴向分段结构, 而非沿轴向整体套装, 其目的是为了减小护套表面涡流损耗.电机结构如图1所示.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 伺服永磁电机结构模型Fig.1 Structure model of permanent magnet synchronous motor

根据上述电机参数选用合适的变频控制器, 搭建了样机测试平台如图2所示.试验时在保证样机电压为额定电压的前提下, 以直流发电机作为负载, 通过改变直流机的励磁电流来控制负载转矩, 最终实现额定负载运行.电机带额定负载运行至温升稳定后测试并记录了电机的相电流.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 电机试验平台Fig.2 Motor test platform

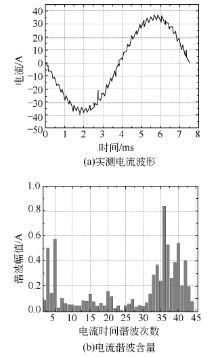
通过试验测得电机额定负载时的电流波形如图3(a)所示.从图中可以看出电流虽接近于正弦, 但因含有电流时间谐波, 电流波形非完全正弦.通过傅里叶分解计算出了各次谐波电流含量, 如图3(b), 从图中可以看出控制器产生的3次、5次及33到42次之间的电流时间谐波的含量比其他次谐波要大, 其中36次电流时间谐波含量最大.由于试验时所用变频器的IGBT开关频率为5 kHz左右, 电机的额定工作频率为133.3 Hz, 受IGBT开关动作的影响, 载波比附近的电流高次谐波幅值较大.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 测试相电流波形及谐波分析Fig.3 Waveform and harmonic amplitudes of testing currents

对电机的电磁场进行分析时, 轴向磁路对电机电磁性能影响不大, 在电磁场求解过程中, 为简化分析, 做出如下假设:

1)忽略电机的端部漏磁, 进行二维电磁场分析时, 向量磁位只考虑 z轴分量Az;

2)电机所用材料均为各向同性;

3)材料的磁导率均匀, 并假设材料的磁导率不随温度变化;

4)忽略分段结构对护套内涡流损耗的影响.

在上述基本假设的基础上, 给定相应的边界条件, 建立的数学模型如下^{[9, 10, 11]}

Ω:∂2Az∂x2+∂2Az∂y2=μσ∂Az∂t-μJzS1:Az=0S2:1μ1∂Az∂n-1μ2∂Az∂n=Js(1)

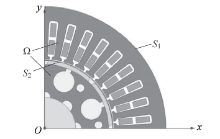
式中:A_z为磁矢位; J_z为传导电流密度; μ 为磁导率; σ 为电导率; t为时间; J_s为永磁体等效电流密度; μ ₁为空气磁导率; μ ₂为永磁体磁导率; Ω 为电机内部求解域; S₁为第1类强加边界条件(定子铁心外圆); S₂为永磁体外边界; n为法向方向.二维泊松方程的求解域是整个电机的内部区域, 电机内任意部位的电磁场均可由式(1)计算得出.模型如图4所示.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 电机二维计算模型Fig.4 2-D electromagnetic calculation model of the prototype

从图3中可看出变频器供电时电机定子电流内产生了大量时间谐波分量.由于定子开槽的影响, 电机定子电流的基波分量所产生的空间谐波磁场会在护套中引起涡流损耗, 同时电流时间谐波将产生时间谐波磁场, 该谐波磁场会在转子导电材料中感应出涡流电流并产生涡流损耗.电机转子由护套、永磁体、转子铁心构成, 其中护套采用导电不导磁的不锈钢材料制成, 其电导率较大, 谐波磁场首先进入护套内并在其中感生出涡流电流, 继而产生损耗, 护套中的涡流会抑制谐波磁场侵入到转子其他部件内.与护套相比, 永磁体的电导率较小, 因此本文所研究的电机结构中永磁体产生的涡流损耗很小可忽略不计.转子铁芯采用很薄的硅钢片压制而成, 切断了涡流的轴向流通, 转子铁心涡流损耗也基本为零.经上述分析可知, 转子护套上的涡流损耗是转子损耗的主要部分.

由于护套紧贴着永磁体, 护套涡流损耗的大小直接影响着护套本身的温升, 其温升也将直接影响永磁体的温度, 因此本文对不同电流谐波在护套中产生的涡流损耗进行详细分析.

涡流损耗在一个周期内的大小为^{[12, 13]}

P=1T∫t0t0+T∑e=1KJe2Δeστ-1lτdt(2)

式中: P为涡流损耗; J_e为单元电密; Δ _e为单元面积; l_τ 为转子有效长度; σ _τ 为护套的电导率.

为对不同电流时间谐波在护套中引起的涡流损耗进行分析, 计算过程分为:

1)将实测电流分解出的电流基波作为激励源, 通过二维瞬态电磁场模型计算出护套中的涡流损耗, 此为电流基波所产生的涡流损耗;

2)在定子绕组通入的电流基波中再分别单独通入主要的电流时间谐波, 并依次进行求解, 分别计算出护套中的涡流损耗, 此为各次谐波分别与基波共同作用时所产生的涡流损耗;

3)将第2步中所得的涡流损耗依次与第1步中的涡流损耗进行比较, 可得出不同的电流谐波单独作用时护套中产生的涡流损耗, 结果如表1所示.

表1

Tab.1

表1(Tab.1)

表1 各次电流在护套中产生的涡流损耗 Tab.1 Eddy current losses of sheath caused by different currents 电流次数 损耗值/W 电流次数 损耗值/W 基波 6.01 37 5.60 5 0.17 39 0 33 0.06 40 6.20 36 0.49 42 0.16

表1 各次电流在护套中产生的涡流损耗 Tab.1 Eddy current losses of sheath caused by different currents

从表1计算的结果可以看出, 大部分3k次电流时间谐波对护套的涡流几乎没有影响, 原因在于电机绕组采用星接法时, 3的整数倍次谐波在三相绕组中相位相同, 相减为零, 3k次谐波磁场几乎没有, 故对护套涡流损耗的影响可以忽略.

由傅里叶分解结果可知, 5次与40次电流时间谐波幅值相近, 通过对这两次谐波在护套中产生的涡流损耗进行比较可知, 在幅值相近时, 频率越高的谐波在转子护套中所产生的涡流损耗越大.这是由于谐波磁场与电机转子的转速不同, 故频率越高的谐波在转子护套中所感生出涡流电流的频率越高, 单位时间内所产生的涡流损耗就越大.从表1可看出, 靠近载波比附近的37次、40次电流时间谐波是涡流损耗的主要来源, 对护套的涡流损耗影响很大.

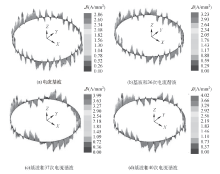
为清晰地看出不同电流时间谐波对涡流损耗的影响, 图5给出了几个主要不同次数电流时间谐波在护套中引起的电密矢量分布图.

尽管36次电流时间谐波含量最大, 但由上述分析可知 3k次电流时间谐波不会产生涡流损耗, 对比可看出图5(a)和5(b)的电密分布基本一致, 图5(b)中的电密部分区域比图5(a)的大是因为36次电流时间谐波引起的空间谐波磁场会产生部分涡流损耗, 但其产生的损耗影响不大.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 护套中的电密矢量分布Fig.5 Vector distribution of current density in sheath

37次和40次电流时间谐波的含量比36次电流时间谐波的含量小得多, 但从图5(c)和5(d)中可以看出其电密分布明显增大, 这是因为非 3k次高次谐波会在护套内产生高频感应电压, 从而产生较大的涡流.

由于样机体积比较小, 电机两端盖散热面积相对较大, 对电机内部温度分布影响比较大.因此, 为了准确计算出电机内的温度分布, 需要建立永磁电机的三维温度场模型.对电机进行温度分析时为简化计算, 提出如下假设:

1)假设材料的导热系数不随温度发生变化;

2)不考虑热辐射对热交换的影响;

3)计算过程中电机所处的环境温度保持不变;

4)电机的初始温度与环境温度一致.

在以上假设的前提下, 确定边值条件, 并对样机的三维温度场方程进行了建立^{[14, 15]}:

∂∂xλx∂T∂x+∂∂yλy∂T∂y+∂∂zλz∂T∂z=-qv-k∂T∂n=αT-Tf (3)

式中: λx, λy, λ _z为材料x, y, z方向的导热系数; q_v为热源密度, 为材料中各项损耗密度之和; T为求解域内任意位置处的温度; α 为求解域边界散热系数; T_f为环境温度.

通过给绕组通入实验电流的基波和所有主要的时间谐波, 对电机的各部分损耗进行计算, 经计算得电机的定子铁心损耗为121.6 W, 绕组铜耗为641.1 W, 护套涡流损耗为18.2 W.

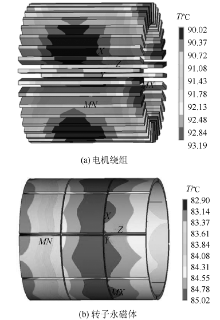
经计算得电机各个部件的损耗, 该损耗即为电机的热源, 给定热源可求解出电机的温度分布.图6中给出基波及各次谐波作用时电机的温度分布.

由于电流基波的幅值为35.7 A, 而电流谐波的幅值最大不超过1 A, 由铜耗计算公式可知本电机中的电流谐波对整体铜耗几乎没有影响, 故可认为加入各次电流谐波后电机的铜耗与基波单独作用时近似相同.所以变频器控制所产生的电流时间谐波主要影响转子护套涡流损耗, 本文主要研究电流谐波产生的护套涡流损耗对永磁体温升的影响, 主要分析了不同电流谐波作用时的永磁体温度的变化.

比较图6中电机各部件的温度分布可看出绕组为电机内温度最高的部件, 这是由于定子绕组的铜耗与电机其他部位的损耗相比要大得多, 且绕组本身的质量及体积并不大, 故而温升最大, 温度最高.图6(a)给出了基波作用时的电机绕组温度分布, 温度分布在88.9 ℃~92 ℃, 其中: MX为最高温度; MN为最低温度.这是由于绕组直线段可经定子铁心通过机壳进行散热, 散热效果较好.绕组端部与定子铁心无接触, 只能通过电机端部腔内的空气进行散热, 电机为密封结构, 端部空气流动较少且空气的导热性比铁心差, 故而端部绕组的温度较高.由图可知电机的温度最高点出现在绕组端部.

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 不同电流时间谐波对电机温度场的影响Fig.6 Motor temperature distribution under different current time harmonics

基波作用时的电机转子护套和永磁体温度分布如图6(b)、6(c)所示, 可以看出护套与永磁体温度分布基本一致, 由于护套与永磁体紧密接触, 故二者温度相同.

比较图6中(c)、(d)、(e)、(f)四幅图可以分别看出5次、37次和40次电流时间谐波对永磁体温度分布的影响.当绕组中只通入电流基波时, 永磁体最高温度为79.6 ℃, 最高温度出现在轴中心偏出风侧处, 加入5次电流谐波时的永磁体的最高温度为79.7 ℃, 与基波单独作用时几乎相等.加入37次和40次电流时间谐波时永磁体的温度发生明显变化, 与基波单独作用时相比, 永磁体最高温度分别升高了2.4 ℃和2.7 ℃.考虑高次谐波的影响, 电机转子护套的涡流损耗与仅有基波作用时相比增加了一倍, 而护套的质量很小, 导致护套及永磁体温度明显上升.

为了更直观看出电流谐波对永磁体温升的影响, 图7中给出了不同谐波作用时永磁体最高温度的变化.图中A、B、C、D、E分别表示电枢绕组中只通入电流基波, 在电流基波中分别加入5次、37次、40次电流时间谐波及基波与所有主要谐波共同作用时的永磁体最高温度变化.

图7

Fig.7

	Figure Option ViewDownloadNew Window
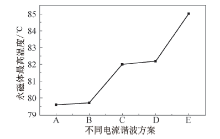	图7 电流时间谐波对永磁体温升的影响Fig.7 Effect of current time harmonics on the temperature rise of permanent magnet

在电机运行时, 电枢绕组中流入的电流不只含有一种谐波, 图8中给出了电流基波与主要时间谐波共同作用时电机各部件的温度分布, 该温度分布即为变频器驱动时的电机温度分布.

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 变频器驱动时电机各部件温度分布Fig.8 Motor parts temperature distribution while driven by inverters

由于电机转子永磁体的温度无法直接测量, 为了验证理论计算与分析的正确性, 在电机的定子绕组内埋有热电偶, 对电机定子绕组温度进行了测量, 绕组实测温度为90 ℃, 计算温度为90 ℃~93.2 ℃, 电机绕组温度的计算值和实测值基本一致, 证明了损耗及温度计算结果的正确性, 因此可认为永磁体的实际温度与计算温度一致.在不考虑护套涡流损耗时, 计算得出永磁体最高温度为 76.5 ℃, 考虑基波及谐波所产生护套涡流损耗的影响时, 永磁体的最高温度变为85 ℃, 护套涡流损耗使得永磁体最高温度升高了8.5℃.通过温度场计算可看出载波比附近的高次电流时间谐波对电机温度场的影响较大, 高次电流谐波使得电机永磁体的最高温度升高了5.4 ℃.通过计算可知, 绕组损耗对永磁体温升的影响较大.与绕组损耗相比, 涡流损耗尽管很小, 但从上述分析可知护套涡流损耗导致永磁体温升增大了10%左右, 两者叠加将有可能使永磁体的工作温度超过其耐温极限从而产生不可逆失磁.由本文的计算及定量分析可知, 控制器驱动时永磁电机定子绕组中的谐波含量的增加将导致永磁体温升明显增大, 使得电机对环境温度的要求更加严苛, 因此减小控制器载波比附近的永磁电机定子绕组电流谐波含量可有效降低永磁体温升.

本文温度场计算和分析在环境温度为10 ℃情况下进行, 环境温度发生改变, 电机各部分温升也会变化.该电机永磁体的工作温度上限为150 ℃, 为保证永磁体工作不因温升过高发生不可逆退磁现象, 因此通过该温度场的计算可以估算该电机应用的环境 温度上限为55 ℃.