光伏阵列双二极管简化模型的建立与仿真

引用本文

贾文婷, 魏学业, 张俊红, 马建光. 光伏阵列双二极管简化模型的建立与仿真[J]. 北京交通大学学报, 2017,41(2): 85-89.
JIA Wenting, WEI Xueye, ZHANG Junhong, MA Jianguang. Modeling and simulation of a photovoltaic two-diode array simplified model[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2017,41(2): 85-89.
Doi:10.11860/j.issn.1673-0291.2017.02.014 复制到剪切板

Permissions

光伏阵列双二极管简化模型的建立与仿真

贾文婷^1,², 魏学业¹, 张俊红¹, 马建光¹

1.北京交通大学电子信息工程学院,北京 100044

2.北京交通职业技术学院城市轨道交通系,北京 102200

通讯作者:魏学业(1963—),男,山东临朐人,教授,博士,博士生导师.email:xywei@bjtu.edu.cn.

第一作者:贾文婷(1984—),女,山西大同人,讲师,博士生.研究方向为光伏发电技术.email:lizzybeijing@126.com.

收稿日期: 2016-09-21

基金: 北京市教育委员会科技计划面上项目(KM20130016014); 北京市优秀人才培养D类项目(2013D005017000008)

摘要

双二极管模型是最能精确表述光伏电池特性的模型,但由于参数过多会增加求解难度,降低求解速度.为此提出一种参数简化的双二极管模型,并设计了对应的算法,将双二极管电流精确化,然后分别利用最大功率匹配法和牛顿迭代法求解参数.通过计算机仿真表明:不同光照和温度下的仿真结果与实际测试阵列的输出相一致,比单二极管Rp模型和双二极管Kashif模型的精度提高了68%和20%,且仿真时间缩短了63%和17%.该简化模型可以为光伏发电系统的优化配置和最大功率点跟踪提供快速和准确的研究基础.

关键词: 光伏阵列; 双二极管模型; 最大功率点匹配; 迭代法

中图分类号:TM914.41 文献标志码:A 文章编号:1673-0291(2017)02-0085-05

Modeling and simulation of a photovoltaic two-diode array simplified model

JIA Wenting^1,², WEI Xueye¹, ZHANG Junhong¹, MA Jianguang¹

1.School of Electronic and Information Engineering,Beijing Jiaotong University,Beijing 100044,China

2.Department of Urban Rail Transit, Beijing Jiaotong Vocational Technical College, Beijing 102200, China

Fund:Science and Technology General Program of Beijing Education Commission(KM20130016014); Training Programme Foundation D for the Talents of Beijing (2013D005017000008)

Abstract

Two-diode model is the most accurate expression to describe the characters of photovoltaic (PV) cell model. But too many parameters will increase the difficulty of the solution, and reduce the speed of the solution. In this paper, a two-diode simplified model is proposed to solve the above problems, and the corresponding algorithm is designed, which increases the current accuracy of the two diodes, and then solves parameters by the maximum power point tracking method and iterative method. The simulation results are consistent with the output results of the actual test array in different irradiation levels and temperatures. The accuracy of the simplified model is increased by 68% and 20% comparing with the single diode model and two-diode Kashif model respectively, and the simulation time is shortened by 63% and 17%, respectively. Therefore the simplified model can be a fast and accurate research basis for the optimization configures and the maximum power point tracking of photovoltaic power generation system.

Keyword: photovoltaic array; two-diode-model; maximum power point matching; iterative method

文章图片

光伏阵列是光伏发电系统的能量提供单元, 其输出特性受到光照和温度等外部环境因素的影响, 研究其输出特性对光伏发电系统的优化配置和最大功率点跟踪具有重要的意义.采用精确可靠的模型有助于准确地反映光伏阵列的输出特性.

近年来, 国内外学者在光伏电池模型建立方向进行了大量的研究工作.最简单的是单二极管模型^{[1, 2, 3]}, 由一个线性独立电流源与一个二极管组成, 这是最理想的电池模型, 模型的待解参数仅有3个, 建模容易和计算简便, 但是与实际光伏电池输出情况偏差较大, 实用性差.在单二极管模型的基础上, 考虑了实际使用中电池存在的接触电阻等电能消耗而引入串联电阻的模型记为 $R_{s}$ 模型^{[4, 5]}, 该模型待解参数为4个, 计算效率较高, 但在高温情况下精度不足.在 $R_{s}$ 模型的基础上考虑了光伏电池由于制造缺陷引起的电能消耗而引入了分路电阻的模型记为 $R_{p}$ 模型^[6], 该模型是最精确地单二极管模型, 待解参数有5个, 在非低照度的情况下能比较精确地反映光伏阵列的输出特性, 但是在低照度情况下精度不足, 而且计算时间较长.与上述模型相比, 双二极管模型^{[7, 8]}考虑了载流子在耗散区的复合损失, 最能全面表征光伏电池特性, 该模型精度较高, 但待解参数有7个, 模型复杂, 计算难度大, 计算时间长.目前常采用文献[7]中学者Kashif Ishaque提出的双二极管模型, 该模型为简化计算将流经两个二极管的电流按相等处理, 将二极管D1的理想因子定为1来处理, 这样的主观假设会影响模型的精确度, 而且连续求解7个参数也增加了模型的计算时间.本文作者主要在光伏电池双二极管模型的基础上推导出参数简化的光伏阵列模型, 设计相应算法, 精确地逐一确定待解参数, 对该简化模型仿真特性进行分析研究.

1 光伏电池单体到阵列的模型推导

1.1 光伏电池单体双二极管的数学模型^[6]

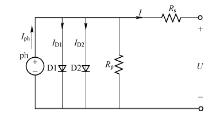
光伏电池双二极管模型等效电路如图1所示, 该模型的输出电压电流关系为

$\begin{array}{l} I = I_{ph} - I_{D 1} - I_{D 2} - \frac{U + I R_{s}}{R_{p}} = \\ I_{ph} - I_{01} [\exp (\frac{U + I R_{s}}{a_{1} v_{T}}) - 1] - \\ I_{02} [\exp (\frac{U + I R_{s}}{a_{2} v_{T}}) - 1] - \frac{U + I R_{s}}{R_{p}} (1) \end{array}$

式中: $I$ 、 $U$ 分别为光伏电池的输出电流和电压; $I_{D 1}$ 、 $I_{D 2}$ 分别为流经两个二极管的电流; $I_{ph}$ 为光伏电池的光生电流; $I_{01}$ 、 $I_{02}$ 分别为两个二极管的反向饱和电流; $R_{s} 为串联电阻, R_{p} 为并联电阻, a_{1}$ 、 $a_{2}$ 分别为两个二极管的理想因子; $v_{T} = KT / q$ , $q$ 为单位电荷为1.6× 10^-19 C, $K$ 为玻尔兹曼常数1.380 6× 10^-22 J/K; $T$ 为光伏电池的绝对温度.

	Figure Option View Download New Window
	图1 光伏电池双二极管模型等效电路Fig.1 Equivalent circuit of double-diode photovoltaic cells model

1.2 光伏阵列双二极管的简化模型

在光伏发电系统中, 若干光伏电池单体串联在一起组成一个光伏组件, 若干光伏组件再通过串并联组成一个光伏阵列.假设所研究光伏阵列由 $m$ 个光伏电池串联组成的光伏组件经过 $n$ 次并联组成, 且所有光伏电池的电气特性完全相同, 其等效电路模型如图2所示.

	Figure Option View Download New Window
	图2 光伏阵列等效电路模型Fig.2 Equivalent circuit model of photovoltaic array

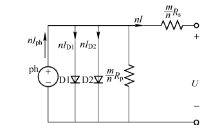
通过下式可以推导得出该光伏阵列的二极管数学模型的输出电压电流特性为

$\begin{array}{l} I = n I_{ph} - n I_{01} \{\exp [\frac{U / m + R_{s} I / n}{a_{1} v_{T}}] - 1\} - \\ n I_{02} \{\exp [\frac{U / m + R_{s} I / n}{a_{2} v_{T}}] - 1\} - \frac{nU + mI R_{s}}{m R_{p}} (2) \end{array}$

式中: $m$ 、 $n$ 为已知量, 故可将 $m$ 、 $n$ 隐含在相应参数中, 即 $I'_{ph} = n \times I_{ph}$ , $I'_{0} = n \times I_{0}$ , $R'_{s} = R_{s} \frac{m}{n}$ , $R'_{p} = R_{P} \frac{m}{n}$ , $v'_{T} = m v_{T}$ , 得出表达式为

$\begin{array}{l} I = I'_{ph} - I'_{01} \{\exp [\frac{U + R'_{s} I}{a_{1} v'_{T}}] - 1\} - \\ I'_{02} \{\exp [\frac{U + R'_{s} I}{a_{2} v'_{T}}] - 1\} - \frac{U + R'_{s} I}{R'_{p}} (3) \end{array}$

比较可得, 式(1)与式(3)一致, 说明 $m \times n$ 的光伏阵列二极管数学模型与光伏电池单体数学模型一致.

模型中可从光伏电池生产商获得的参数有:标准条件下(世界公认的地面光伏组件标准测试条件STC为大气质量AM1.5, 温度为25 ℃、照度为1 000 W/m²)开路电压 $U_{oc_STC}$ 、短路电流 $I_{sc_STC}$ 、最大输出功率 $P_{m_STC}$ 、最大功率点电压 $U_{m}$ 、最大功率点电流 $I_{m}$ 、开路电压温度系数 $K_{V}$ 、短路电流温度系数 $K_{I}$ .待解参数有:光生电流 $I_{ph}$ 、二极管理想因子 $a_{1}$ 和 $a_{2}$ 、串联电阻 $R_{s}$ 、并联电阻 $R_{p}$ 、二极管反向饱和电流 $I_{01}$ 、 $I_{02}$ .在非线性方程中求解7个参数会导致模型复杂, 计算时间增长.本文借鉴参考文献[8]观点, 在模型中简化串联电阻 $R_{s}$ 、并联电阻 $R_{p}$ , 在保证模型精确度的同时大大节约了计算时间.故光伏阵列的双二极管数学简化模型最终输出特性表达为

$I = I_{ph} - I_{01} [\exp (\frac{U}{a_{1} v_{T}}) - 1] - I_{02} [\exp (\frac{U}{a_{2} v_{T}}) - 1] (4)$

2 双二极管简化模型参数确定

2.1 光生电流I_ph的确定

$I_{ph}$ 为光伏电池产生电流, 与环境温度和光照度有关, 表达式^[9]为

$I_{ph} = (I_{sc_STC} + K_{I} ΔT) \frac{G}{G_{STC}} (5)$

式中: $△ T = T - T_{STC}$ , $T_{STC}$ 为标准温度298 K; $G$ 为电池表面光照度; $G_{STC}$ 为标准照度1 000 W/m², $K_{I}$ 与 $I_{sc_STC}$ 可从厂家提供的参数获得.

2.2 二极管反向饱和电流I₀₁、I₀₂的确定

$I_{01}$ 为简单二极管反向饱和电流, 表达式为

$I_{01} = \frac{(I_{sc_STC} + K_{I} ΔT)}{\exp (\frac{U_{oc_STC} + K_{V} ΔT}{v_{T} a_{1}} - 1)} (6)$

通常 $I_{01}$ 与 $I_{02}$ 具有如下数量关系为

$I_{02} = (\frac{T^{2 / 5}}{3.77}) I_{01} (7)$

2.3 二极管理想因子a₁、a₂的确定

将式(5~7)代入式(4)可知, 输出关系式中的未知量为二极管理想因子 $a_{1}$ 、 $a_{2}$ .此时代入开路电压 $U = U_{oc_STC}$ , $I$ =0 A, 可得 $a_{1}$ 、 $a_{2}$ 的关系式为

$a_{2} = \frac{U_{oc_STC}}{v_{T} \ln (\frac{I_{ph} - I_{01} [\exp (U_{oc_STC} / v_{T} a_{1}) - 1]}{I_{02}} + 1)} (8)$

其中: $a_{1}$ 、 $a_{2}$ 迭代算法如下:

1)由肖克利的扩散电流理论可知, 对于普通二极管其理想因子一般在1~2之间, 故 $1 \leq a_{1} \leq 2$ , 可将 $a_{1}$ 的初始值设为1.通过增加 $a_{1}$ 的值, 采用牛顿迭代法代入式(8)求解得出相应的 $a_{2}$ .

2)将所得的 $a_{1}$ 、 $a_{2}$ 代入式(4)可得 $U - I$ 关系式, 并在 $[0$ $U_{oc}]$ 区间内求解 $U_{m_cal}$ 、 $I_{m_cal}$ , 使具有最大功率点 $P_{m_cal} = U_{m_cal} I_{m_cal}$ .

3)利用最大功率匹配法将 $P_{m_cal}$ 与光伏电池生产厂商提供的 $P_{m_STC}$ 进行比较, 如果在误差范围内, 即此 $a_{1}$ 、 $a_{2}$ 为最终值; 如果不能满足误差要求, 则继续迭代求解下一组 $a_{1}$ 、 $a_{2}$ 值, 计算流程如图3所示, 使用Matlab/Simulink环境下的基本数学模块建立模型.

	Figure Option View Download New Window
	图3 确定 $a_{1}$ 、 $a_{2}$ 值的算法流程图Fig.3 Algorithm flow chart of confirming the value of $a_{1}$ 、 $a_{2}$

3 仿真验证

搭接试验电路, 采用KG200GT光伏电池组件进行数据采集试验, 采集该光伏阵列在不同条件下的电压电流输出特性.KG200GT光伏电池组件电气参数见表1.

表1 KG200GT光伏电池组件电气参数 Tab.1 Electrical parameters of photovoltaic module of KG200GT

参数名称	参数数值 $(m = 54, n = 1)$
最大功率 $P_{m_STC}$ / W	200
短路电流 $I_{sc_STC}$ / A	8.2
开路电压 $U_{oc_STC}$ / V	32.9
最大功率点电压 $U_{m}$ / V	26.3
最大功率点电流 $I_{m}$ / A	7.61
开路电压温度系数 $K_{V}$ / (mV/K )	-123
短路电流温度系数 $K_{I}$ / (mA/K)	3.18

表1 KG200GT光伏电池组件电气参数 Tab.1 Electrical parameters of photovoltaic module of KG200GT

3.1 双二极管模型仿真参数计算结果

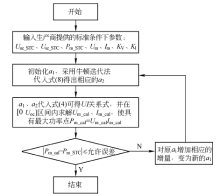
利用Matlab编程仿真, 计算出相应参数 $I_{ph} 、 I_{01} 、 I_{02},$ 然后通过最大功率匹配方法迭代求解得出a₁、a₂ 值.表2为求解所得KG200GT的电气参数.

表2 求解所得KG200GT的电气参数 Tab.2 Obtained electrical parameters of KG200GT

参数名称	参数值
光生电流 $I_{ph}$ / A	8.19
二极管反向饱和电流 $I_{01}$ / A	$5.011 9 \times 10^{- 4}$
二极管反向饱和电流 $I_{02}$ / A	1.298× 10^-5
二极管理想因子 $a_{1}$	1.68
二极管理想因子 $a_{2}$	2.52

表2 求解所得KG200GT的电气参数 Tab.2 Obtained electrical parameters of KG200GT

3.2 双二极管简化模型输出特性分析

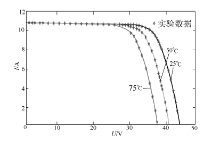
在标准温度为25 ℃时, 仿真KG200GT光伏组件分别在 $G$ =1 000 W/m², $G$ =800 W/m², $G$ =600 W/m², $G$ =400 W/m²时, $I⁃U$ 特性的仿真曲线和实验数据见图4.

在标准照度为1 000 W/m²时, 仿真光伏阵列分别在25 ℃, 50 ℃, 75 ℃时, 图5 不同温度下的I-U仿真曲线和实验数据.

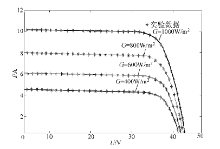	Figure Option View Download New Window
	图4 不同照度下的I-U仿真曲线和实验数据Fig.4 $I⁃U$ Simulation curves and experimental data under different irradiation levels

	Figure Option View Download New Window
	图5 不同温度下的I-U仿真曲线和实验数据Fig.5 I-U simulation curves and experimental data at different temperatures

由图5 不同温度下的 $I⁃U$ 仿真曲线和实验数据可知, 本文提出的双二极管简化模型所得 $I⁃U$ 曲线与实验数据基本保持一致.在较低照度400 W/m², 较高温度75 ℃时, 依然与实验数据保持较好的吻合.在开路电压点、短路电流点和最大功率点的值精确度也较高.

3.3 与其他模型输出特性比较

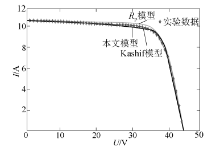将KG200GT电池组件在光照强度为1 000 W/m², 温度为25 ℃的标准环境条件下, 分别用 $R_{p}$ 模型、文献[7]中Kashif Ishaque提出的双二极管模型和本文提出的双二极管简化模型进行仿真, 将仿真后的输出特性与实验数据进行对比, 图6为标准环境下3个模型的仿真曲线与实验数据对比.

	Figure Option View Download New Window
	图6 标准环境下3个模型的仿真曲线与实验数据对比Fig.6 Comparison of simulation curves and experimental data of three models under standard environment

在标准环境下, 本文的双二极管简化模型算法其 $I⁃U$ 仿真曲线与实际的测量数据基本吻合, 与 $R_{p}$ 模型和文献[7]中提出的双二极管模型相比优势较为明显.

经过测试可得:采用其他型号的电池和设置不同的串并联结构(即设置不同的 $m 、 n$ 值), 结果均符合上述结论.因此, 可确定该模型适用于各种型号电池组成的光伏阵列.

3.4 与其他模型的精度和仿真时间比较

图7为3种模型与实验数据的绝对误差比较, 可知3种模型的误差率都相对较低, 但比较本文提出的双二极管模型与实验数据的相对误差更小, 更精确.

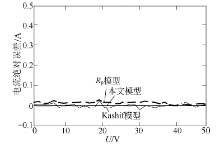	Figure Option View Download New Window
	图7 3种模型与实验数据的绝对误差比较Fig.7 Comparison of the absolute error between the three models and the experimental data

为了从数量角度衡量3种模型的精度, 可计算3种模型的仿真数据与实验数据的均方根误差(RMSE), 来衡量仿真数据与实验数据之间的偏差程度, 见表3.

表3 3种模型的RMSE和仿真时间比较 Tab.3 Comparison based on RMSE and simulation time of three models

模型名称	电流RMSE/A	仿真时间/s
本文模型	0.08	0.10
$R_{p}$ 模型	0.25	0.27
Kashif模型	0.10	0.12

表3 3种模型的RMSE和仿真时间比较 Tab.3 Comparison based on RMSE and simulation time of three models

由表4比较可得3种模型中, 本文模型RMSE为0.08 A是最小, 表明本文模型与实验数据最接近, 与 $R_{p}$ 模型相比, 精度提高了68%; 与Kashif模型相比精度提高了20%.

将3种模型在同一台计算机以完全相同的运行环境进行仿真, 记录3种模型的仿真时间并进行比较, 见表3.本文模型仿真时间为0.10 s, 与 $R_{p}$ 模型相比, 仿真时间缩短了63%; 与Kashif模型相比仿真时间缩短了17%.

4 结论

1)本文作者提出光伏阵列双二极管简化模型, 并设计了相应的算法求解未知参数.简化后的模型降低了计算难度, 加快了计算速度, 提高了模型的精度.模型建立过程中没有对任何参数进行主观假设, 所有参数都参与了合理的分析和计算.

2)通过仿真验证, 本文模型在不同光照和温度条件下与实验光伏电池保持输出特性一致, 能准确反映最大功率点处输出特性, 该模型与 $R_{p}$ 模型、Kashif模型相比具有更高的精确度和更快的仿真速度.本文设计的光伏阵列简化模型应用于光伏发电系统优化配置和最大功率点追踪, 可以更加快速和准确地描述出光伏阵列的输出特性.

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	TAN Y T, KIRSCHEN D S, JENKINS N. A model of PV generation suitable for stability analysis[J]. IEEE Transactions on Energy Conversion, 2005, 19(4): 748-755. [本文引用:1]
[2]	GLASS M C. Improved solar array power point model with SPICE realization[C]. Energy Conversion Engineering Conference, 1996, 1: 286-291. [本文引用:1]
[3]	XIAO W, DUNFORD W G, CAPEL A. A novel modeling method for photovoltaic cells[C]. IEEE Power Electronics Specialists Conference, 2004, 3: 1950-1956. [本文引用:1]
[4]	YADIR S, BENHMIDA M, SIDKI M. New method for extracting the model physical parameters of solar cell using explicit analytic solutions of current-voltage equation[C]. International Conference on Microelectronics, 2009: 390-393. [本文引用:1]
[5]	LIU S, DOUGAL R A. Dynamic mutiphysics model for solar array[J]. IEEE Transactions on Energy Conversion, 2002, 17(2): 285-294. [本文引用:1]
[6]	SOTO W D, KLEIN S A, BECKMAN W A. Improvement and validation of a model for photovoltaic array performance[J]. Solar Energy, 2006, 80(1): 78-88. [本文引用:2]
[7]	KASHIF I, SALAM Z, TAHERI H. Simple fast and accurate two-diode model for photovoltaic modules[J]. Solar Energy Materials & Solar Cells , 2011, 95(2): 586-594. [本文引用:4]
[8]	SALAM Z, ISHAQUE K, TAHERI H. An improved two-diode photovoltaic (PV) model for PV system[C]. Joint International Conference on Power Electronics, 2011: 1-5. [本文引用:2]
[9]	张俊红, 魏学业, 祝天龙. 光伏阵列建模和仿真特性研究[J]. 计算机仿真, 2014, 31(3): 134-138. ZHANG Junhong, WEI Xueye, ZHU Tianlong. Research on modeling and characteristic simulation of photovoltaic array[J]. Computer Simulation, 2014, 31(3): 134-138. (in Chinese) [本文引用:1]

2005

0.0

... 最简单的是单二极管模型^[1,2,3],由一个线性独立电流源与一个二极管组成,这是最理想的电池模型,模型的待解参数仅有3个,建模容易和计算简便,但是与实际光伏电池输出情况偏差较大,实用性差 ...

1996

0.0

2004

0.0

2009

0.0

... 在单二极管模型的基础上,考虑了实际使用中电池存在的接触电阻等电能消耗而引入串联电阻的模型记为 Rs模型^[4,5],该模型待解参数为4个,计算效率较高,但在高温情况下精度不足 ...

2002

0.0

2006

0.0

... 在 Rs模型的基础上考虑了光伏电池由于制造缺陷引起的电能消耗而引入了分路电阻的模型记为 Rp模型^[6],该模型是最精确地单二极管模型,待解参数有5个,在非低照度的情况下能比较精确地反映光伏阵列的输出特性,但是在低照度情况下精度不足,而且计算时间较长 ...

... 1 光伏电池单体双二极管的数学模型^[6]光伏电池双二极管模型等效电路如图1所示,该模型的输出电压电流关系为 ...

2011

0.0

... 与上述模型相比,双二极管模型^[7,8]考虑了载流子在耗散区的复合损失,最能全面表征光伏电池特性,该模型精度较高,但待解参数有7个,模型复杂,计算难度大,计算时间长 ...

... 目前常采用文献[7]中学者Kashif Ishaque提出的双二极管模型,该模型为简化计算将流经两个二极管的电流按相等处理,将二极管D1的理想因子定为1来处理,这样的主观假设会影响模型的精确度,而且连续求解7个参数也增加了模型的计算时间 ...

... 3 与其他模型输出特性比较将KG200GT电池组件在光照强度为1 000 W/m²,温度为25 ℃的标准环境条件下,分别用 Rp模型、文献[7]中Kashif Ishaque提出的双二极管模型和本文提出的双二极管简化模型进行仿真,将仿真后的输出特性与实验数据进行对比,图6为标准环境下3个模型的仿真曲线与实验数据对比 ...

... 在标准环境下,本文的双二极管简化模型算法其 I⁃U仿真曲线与实际的测量数据基本吻合,与 Rp模型和文献[7]中提出的双二极管模型相比优势较为明显 ...

2011

0.0

... 本文借鉴参考文献[8]观点,在模型中简化串联电阻 Rs、并联电阻 Rp,在保证模型精确度的同时大大节约了计算时间 ...

2014

0.0

张俊红, 魏学业, 祝天龙. 光伏阵列建模和仿真特性研究[J]. 计算机仿真, 2014, 31(3): 134-138.

ZHANG

Junhong

, WEI

Xueye

, ZHU

Tianlong

. Research on modeling and characteristic simulation of photovoltaic array[J]. Computer Simulation, 2014, 31(3): 134-138. (in Chinese)

... 1 光生电流I_ph的确定Iph为光伏电池产生电流,与环境温度和光照度有关,表达式^[9]为 ...