一种改进的MMC电容电压均衡控制方法

引用本文

郑连清, 徐江涛, 马世强. 一种改进的MMC电容电压均衡控制方法[J]. 北京交通大学学报, 2017,41(2): 112-116.
ZHENG Lianqing, XU Jiangtao, MA Shiqiang. An improved control method for MMC capacitor voltage balancing[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2017,41(2): 112-116.
Doi:10.11860/j.issn.1673-0291.2017.02.018 复制到剪切板

Permissions

一种改进的MMC电容电压均衡控制方法

郑连清¹, 徐江涛¹, 马世强²

1. 重庆大学输配电装备及系统安全与新技术国家重点实验室,重庆400044

2. 新疆生产建设兵团兴新职业技术学校,乌鲁木齐830074

第一作者:郑连清(1964—),男,浙江金华人,教授,博士. 研究方向为电力电子在电力系统中的应用.email: lqzheng64@cqu.edu.cn

收稿日期: 2016-09-09

基金: 国家自然科学基金(51577020)

摘要

电容电压排序法是一种简单有效的MMC电容电压均衡方法,传统的排序算法会导致子模块反复投切,造成器件开关频率过高,增加了MMC的运行损耗.为此提出了一种改进的方法,即由允许的电容电压偏差大小和桥臂电流计算出维持子模块电压均衡所需的最小排序频率,并将排序频率控制在该最小值处,减少了不必要的子模块投切次数,从而在较低的开关频率下维持各子模块电压的均衡.在Simulink中搭建了MMC仿真模型,对改进前后的两种方法进行对比,仿真结果表明:改进的排序法能够有效降低开关频率,降幅可达70%.

关键词: 模块化多电平变换器; 电压均衡; 变频排序; 开关频率

中图分类号:TM464 文献标志码:A 文章编号:1673-0291(2017)02-0112-05

An improved control method for MMC capacitor voltage balancing

ZHENG Lianqing¹, XU Jiangtao¹, MA Shiqiang²

1. State Key Laboratory of Power Transmission Equipment and System Security and New Technology ,Chongqing University, Chongqing 400044, China

2.Xingxin Vocational and Technical College of Xinjiang Province and Construction Corps, Urumqi 830074,China

Fund:National Natural Science Foundation of China(51577020)

Abstract

The capacitor voltage sorting algorithm is a simple and effective method for equalizing MMC( Modular Multilevel Converter) capacitor voltages. However, the traditional sort algorithm leads to the submodules switched repeatedly. The high switching frequency increases the system loss. Therefore, an improved method is proposed, which can reduce the switching frequency by controlling the sorting frequency. The sorting frequency is the minimum for equalizing voltages that is calculated by the capacitor voltage difference and arm current. So the submodule voltages can be equalized at a low switching frequency. Finally, a MMC simulation model is built in Simulink to compare the two methods before and after the improvement. The simulation results show that the improved sorting method can effectively reduce the switching frequency, which the reduction is up to 70%.

Keyword: modular multilevel converter; voltages balancing; variable-frequency sort; switching frequency

文章图片

模块化多电平变换器(Modular Multilevel Converter, MMC) , 在2001年由文献[1]R. Marquardt首次提出.MMC是一种级联结构的电压源型变换器, 具有承受高电压且输出电压谐波含量低、无需滤波器的优点.MMC解决了变换器对柔性直流输电的容量限制, 在高压直流输电领域具有良好的应用前景^[2].国内外的研究人员针对MMC的相关问题展开了深入的研究^{[3, 4, 5]}, 其中, 子模块电压均衡控制是MMC控制中关键技术之一^{[6, 7, 8]}.

MMC电容电压排序法由于原理简单、易于实现和应用范围不受限制等特点, 在理论研究和工程应用中都更具优势.然而传统的排序算法无条件地作用于每个触发过程, 即使子模块电压之间的差异很小, 其排序结果也会发生改变, 从而改变子模块的投切状态, 造成子模块不必要的反复投切, 导致过高的开关频率, 增加MMC的运行损耗.为了降低开关频率, 文献[9]提出了一种优化的均压方法, 通过存储子模块投切状态, 使其尽可能保持原有状态, 有效地降低了开关频率.文献[10]通过限制排序次数, 只在切入的子模块数发生变化时, 才对电容电压进行排序, 虽然能够降低开关频率, 但受子模块数量的影响实际应用效果不佳.文献[11]提出了保持因子法, 通过保持因子稳固子模块的排序位置, 使各子模块具有一定保持原来投切状态的能力, 一定程度上降低开关器件的开关频率.文献[12]采用双保持因子法和分组排序法, 既降低了开关频率又提高了排序速度.文献[13]通过设置触发条件在传统排序法和优化的排序算法之间进行选择, 降低开关频率的程度有限.文献[14]通过比较前后控制周期中投入子模块的个数及判断各桥臂子模块的电容电压与其平均值的偏差是否越界, 来决定是否重新计算触发脉冲, 提出了一种无需排序的均衡控制策略.以上这些优化方法, 相对复杂不利于工程应用.

经过分析可知, 采用电容电压排序均压法时, 降低开关频率的关键在于控制排序频率, 避免电容电压的微小变化对排序结果的影响, 进而影响子模块投切.本文作者提出了变频排序法, 减少了不必要的开关动作, 使子模块电压在较低的开关频率下保持均衡.

1 MMC工作原理

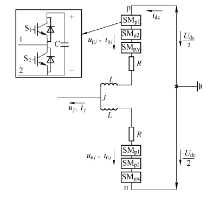
图1为MMC主电路和子模块的拓扑结构, 其桥臂由 $N$ 个子模块级联而成, 子模块采用典型的半桥结构, L为桥臂电感, R为桥臂等效电阻.MMC正常工作时子模块中的两个IGBT互补导通, 上管S₁导通, 下管S₂关断为切入子模块, 反之为切出.子模块端口“ 1” 和“ 2” 之间的电压为U_SM, 切入子模块时U_SM=U_C, 切出子模块时则为U_SM=0.控制MMC各相上、下桥臂切入子模块的个数即可控制其交流输出电压.

	Figure Option View Download New Window
	图1 MMC拓扑结构Fig. 1 Topological structure of MMC

根据图1, 由KVL得

$\{\begin{array}{l} u_{j} = \frac{U_{dc}}{2} - u_{p j} - L \frac{d i_{p j}}{d t} - R i_{p j} \\ u_{j} = - \frac{U_{dc}}{2} + u_{n j} + L \frac{d i_{n j}}{d t} + R i_{n j} \end{array} (1)$

于是 $j 相输出电压 u_{j}$ 为

$u_{j} = \frac{u_{n j} - u_{p j}}{2} - (\frac{L}{2} \frac{d i_{j}}{d t} + \frac{R i_{j}}{2}) (2)$

式中, j(j=a, b, c)相的输出电压u_j随着j相上、下桥臂电压u_pj和u_nj之差的变化而变化.

控制MMC上、下桥臂切入子模块的个数即可控制u_pj和u_nj, 从而控制j相输出电压.因此可以根据输出电压u_j确定上、下桥臂应切入的子模块数N_pj和N_nj, 此外也可以采用载波移相或载波层叠等PWM调制法得到各个子模块的驱动信号, 然后统计“ 使子模块切入的” 驱动信号的个数, 从而得到N_pj和N_nj为

$\{\begin{array}{l} N_{p j} = \frac{N}{2} - round {[\frac{u_{j}}{U_{SM}}]}_{x_{1}} \\ N_{n j} = \frac{N}{2} + round {[\frac{u_{j}}{U_{SM}}]}_{x_{2}} \end{array} (3)$

式中: $u_{j} 为 j$ 相输出电压; round为取整函数; $x_{1} 和 x_{2} 分别为计算 N_{p j} 和 N_{n j}$ 时取整函数的阈值, 其取值范围是(0, 1), 取整方法为小数部分小于阈值直接舍去, 否则进一, 如round[5.30]_0.3=6, round[5.29]_0.3=5.当 $x_{1} = x_{2} = 0.5 时,$ 取整方式为最近取整, 对应的调整方法被称为最近电平调制.

2 MMC电容电压变频排序法

经过调制确定了上、下桥臂所需切入的子模块数, 但并没有指明具体的子模块, 均压策略则是根据 $N_{p j} 和 N_{n j}$ 确定具体要切入的子模块.

2.1 传统排序法分析

传统的电容电压排序法是一种行之有效的均压方法, 按照恒定的频率将子模块按照电压大小排序, 然后在子模块充电时切入电压较低的子模块, 放电时切入电压较高的子模块, 通过“ 高放低冲” 的方法实现了子模块电压的均衡.在实际的MMC控制中, 各子模块电压经过AD采样再送入主控制器中进行排序, 由于控制器处理速度较快, 因此排序频率主要取决于采样频率.采样频率过低, 可能会使输出电压丢失电平、增加谐波含量^[15].因此采样频率必须设置的足够高.而过高的采样频率必然导致排序频率较高, 子模块电压在下一次采样时电压大小发生了微小的变化, 使得排序结果发生改变, 传统排序算法将根据投切规则重新分配触发脉冲.子模块的投切状态随之发生改变, 上一个控制周期被切入的子模块在当前周期可能部分甚至全部被切出, 下一个控制周期时又重复这一过程.子模块频繁的切入又切出主电路, 虽然保证了子模块电压的均衡, 但必然造成过高的开关频率, 产生较大的损耗.

2.2 变频排序法

从对传统排序法的分析可知, 降低开关频率可以通过降低排序频率来实现, 但是排序频率太低会使子模块之间产生较大的电压偏差.由于子模块电容电压的变化与桥臂电流相关, 为了平衡均压效果和开关频率之间的矛盾, 排序频率应随着桥臂电流的变化而变化, 故本文提出了变频排序均压法.

变频排序法的思想:MMC子模块电容电压的变化与桥臂电流相关, 无论充电还是放电, 桥臂电流越大子模块电容电压变化越快.为了控制各子模块电压之间的偏差, 当桥臂电流较大时就要增加排序频率减小电容充放电时间, 反之可以减小排序频率.根据桥臂电流大小可以计算出使子模块电压偏差不超过允许值的最小排序频率, 然后通过触发控制排序, 将排序频率控制在这个最小频率点附近, 排序频率将随着桥臂电流的大小而改变, 从而降低器件开关频率, 同时保持子模块电压的稳定.

假设允许的子模块电压偏差最大值为子模块电压U_SM的δ %, 子模块电容电压的排序频率为f_p, 在一个排序周期内桥臂电流的平均值为i_ba, 子模块电容为C, 则有

$\frac{i_{ba}}{f_{p} C} = Δ U_{c} \leq U_{SM} δ % (4)$

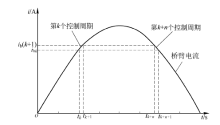
式中可知, 为了将子模块电压偏差维持在一定范围, 排序频率f_p应随着i_ba的增大而增大.同时根据i_ba的大小利用式(4)可以计算出f_p的最小值.图2为桥臂电流的采样示意图.

	Figure Option View Download New Window
	图2 桥臂电流采样示意图Fig. 2 Schematic diagram of bridge arm current sampling

由于桥臂电流i_b实时变化(可能增大也可能减小), 故当前控制周期内桥臂电流平均值i_ba 无法得到.考虑到一个控制周期i_b变化幅度极小且连续变化, 故可以用采样时刻的桥臂电流i_b 来代替i_ba.由于桥臂电流为交流量, 其采样值可能为0, 所以直接用式(4)计算f_p, 其结果可能出现f_p=0, 这种情况一定要避免, 此外i_b可能会小于i_ba, 此时计算结果会偏小, 因此根据i_b计算出f_p后, 还应增加一个补偿频 $率 Δ f, 则 f_{p}$ 的计算表达式为

$f_{p} = \frac{| i_{b} |}{C U_{SM} δ %} + Δf (5)$

式(5)得到的排序频率f_p是保证子模块电压稳定的最小排序频率, 将排序频率控制为f_p就能达到降低开关频率的目的.采用变频排序法时主要考虑补偿频率Δ f的第1种作用, 即避免f_p=0.当i_b=0时, 计算出的排序频率取得最小值f_p=Δ f, 为避免下一次i_b的采样值仍为0, 则Δ f应大于桥臂电流频率的2倍, 即 $Δ f > 100 Hz.$

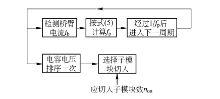
根据以上原理, 本文作者设计了变频排序控制系统如图3所示.在每个控制周期开始首先检测桥臂电流大小并对桥臂上的电容电压进行排序, 根据排序结果选择子模块切入, 然后按式(5)计算出 $f_{p}, 经过 1 / f_{p}$ 的时间后进行下一次排序.这样一来每个控制周期内, 电容电压只进行一次排序, 排序频率始终控制在保持子模块电压均衡的最小频率处, 减少了非必要的排序次数, 从而降低了器件的开关频率.

	Figure Option View Download New Window
	图3 变频排序控制系统Fig.3 Variable-frequency sorting control system

3 仿真验证

为了验证本文提出的变频排序法减小器件开关频率的有效性, 在Simulink中搭建了三相MMC仿真模型, 对传统的恒频排序法和本文的变频排序法进行比较, 仿真参数设置如表1 所示.

表1 仿真模型参数 Tab.1 Parameters of simulation model

根据文献[15]采用传统的恒频排序法时, 采样频率应满足: f_c≥ k• π • f• N=1 570Hz, 故仿真中设置f_c=2 000Hz.文献[11, 16]指出MMC正常工作时子模块电压之间的偏差应小于5%, 根据补偿频率Δ f的值取要求, 仿真中设置为Δ f=120Hz.采用最近电平调制, 对两种均压方法进行比较.

以A相上桥臂子模块电压为比较对象, 采用传统排序均压法得到的各子模块电容电压的仿真波形见图4.图5(a)~(d)分别为采用变频排序均压法在不同 $δ$ 值下A相上桥臂各子模块电容电压的波形.

	Figure Option View Download New Window
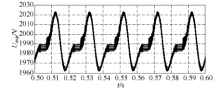	图4 传统排序均压法的电容电压波形Fig. 4 Capacitor voltage waveforms with traditional sorting voltage balancing method

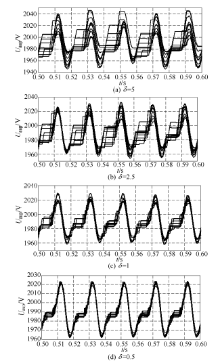	Figure Option View Download New Window
	图5 变频排序均压法的电容电压波形Fig. 5 Capacitor voltage waveforms with variable frequency sorting voltage balancing method

根据图4和图5中电容电压的波形可知, 传统排序法和变频排序法均能控制子模块的电容电压保持稳定.在传统排序法下, 各子模块电容电压的一致性较好, 不同子模块之间的电压偏差始终很小; 而采用变频排序法时子模块之间的电压会有一定的差异, 但电压偏差小于事先设定的允许值, 对比图5 (a)~(d)可知, 随着允许电压偏差 $δ$ 值的减小, 子模块电容之间的电压偏差逐渐减小, 电容电压波动幅度变小.当 $δ = 0.5$ 时, 两种方法下的电容电压波形基本相同.

为了比较两种方法下的开关频率, 分别以A相上、下桥臂 (N个子模块开关次数的平均值f_sa作为单个器件的开关频率进行比较.@两种电压均压方法下器件的平均开关频率如表2所示.)

表2 开关频率对比 Tab. 2 Comparison of switching frequency

均压方法		器件开关频率 $f_{s} / Hz$
恒频排序法		380.3(上)383.0(下)
变频排序法	$δ = 5.0$	104.9(上)105.5(下)
	$δ = 2.5$	132.0(上)132.1(下)
	$δ = 1.0$	206.2(上)205.1(下)
	$δ = 0.5$	332.5(上)333.1(下)

表2 开关频率对比 Tab. 2 Comparison of switching frequency

表2中的结果表明:本文提出的变频排序法通过控制排序频率可以实现降低器件开关频率的目的, 从而降低了MMC的运行损耗.采用变频排序均压法时, δ 的取值不同, 开关频率减小的程度不同, δ 越大开关频率越低, 当δ = $5$ 时开关频率仅为传统排序法的27.6%, 开关频率降低了近70%.实际应用中只要确定了子模块电容电压偏差的允许值 $δ,$ 即可采用变频排序法最大限度地减小开关频率.

4 结论

1)本文作者提出了MMC电容电压变频排序法, 通过控制排序频率, 使其随着桥臂电流的变化而变化, 其大小始终维持在均衡子模块电压所必须的排序次数, 避免了非必要的排序次数, 从而降低了开关频率减小了MMC运行损耗.

2)由于排序的频率是根据系统对子模块电压偏差的允许值计算得到, 因此子模块电容电压之间的差值能够控制在子模块参考电压的5%以内, 保证了子模块电压的稳定.在实际应用中, 可以减小 $δ 的取值, 比如取 δ = 2.5,$ 此时子模块之间的电压偏差较小且开关频率仅为传统排序法的35%.仿真结果验证了MMC变频排序法在减小开关频率、降低开关损耗方面的有效性.

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	MARQUARDT R. Stromrichterschaltungen Mit vertei-lten energiespeichern: German: DE10103031A1[P]. 2001. [本文引用:1]
[2]	马为民, 吴方劼, 杨一鸣, 等. 柔性直流输电技术的现状及应用前景分析[J]. 高电压技术, 2014, 40(8): 2429-2439. MA Weimin, WU Fangjie, YANG Yiming, et al. Flexible HVDC transmission technology’s today and tomorrow[J]. High Voltage Engineering, 2014, 40(8): 2429-2439. (in Chinese) [本文引用:1]
[3]	孙浩, 杨晓峰, 支刚, 等. CPS-SPWM在模块组合多电平变换器中的应用[J]. 北京交通大学学报, 2011, 35(5): 131-136. SUN Hao, YANG Xiaofeng, ZHI Gang, et al. Application of carrier phase-shifted SPWM in the modular multilevel converter[J]. Journal of Beijing Jiaotong University, 2011, 35(5): 131-136. (in Chinese) [本文引用:1]
[4]	MEI J, JI Y, TIAN J, et al. Balancing control schemes for modular multilevel converters using virtual loop mapping with fault tolerance capabilities[J]. IEEE Transactions on Industrial Electronics, 2016, 63(1): 38-48. [本文引用:1]
[5]	LEE H J, JUNG J, SUL S K. A switching frequency reduction and a mitigation of voltage fluctuation of modular multilevel converter for HVDC[C]. IEEE Energy Conversion Congress and Exposition, 2014: 483-490. [本文引用:1]
[6]	李笑倩, 宋强, 刘文华, 等. 采用载波移相调制的模块化多电平换流器电容电压平衡控制[J]. 中国电机工程学报, 2012, 32(9): 49-55. LI Xiaoqian, SONG Qiang, LIU Wenhua, et al. Capacitor voltage balancing control by using carrier phase-shift modulation of modular multilevel converters[J]. Proceedings of the CSEE, 2012, 32(9): 49-55. (in Chinese) [本文引用:1]
[7]	MESHRAM P M, BORGHATE V B. A simplified nearest level control voltage balancing method for modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 450-462. [本文引用:1]
[8]	杨晓峰, 林智钦, 郑琼林, 等. 模块组合多电平变换器的研究综述[J]. 中国电机工程学报, 2013, 33(6): 1-14. YANG Xiaofeng, LIN Zhiqin, ZHENG Trillion Q, et al. A review of modular multilevel converters[J]. Proceedings of the CSEE, 2013, 33(6): 1-14. (in Chinese) [本文引用:1]
[9]	屠卿瑞, 徐政, 郑翔, 等. 一种优化的模块化多电平换流器电压均衡控制方法[J]. 电工技术学报, 2011, 26(5): 15-20. TU Qingrui, XU Zheng, ZHENG Xiang, et al. An optimized voltage balancing method for modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2011, 26(5): 15-20. (in Chinese) [本文引用:1]
[10]	武晓堃, 王奎, 万磊, 等. 模块化多电平变换器三种调制策略及电压平衡控制仿真与对比研究[J]. 电工电能新技术, 2014, 33(12): 4-9. WU Xiaokun, WANG Kui, WAN Lei, et al. Simulation and comparative study of three modulation strategies and voltage balance control in modular multilevel converter[J]. Advanced Technology of Electrical Engineering and Energy, 2014, 33(12): 4-9. (in Chinese) [本文引用:1]
[11]	管敏渊, 徐政. MMC型VSC-HVDC系统电容电压的优化平衡控制[J]. 中国电机工程学报, 2011, 31(12): 9-14. GUAN Minyuan, XU Zheng. Optimized capacitor voltage balancing control for modular multilevel converter based VSC-HVDC system[J]. Proceedings of the CSEE, 2011, 31(12): 9-14. (in Chinese) [本文引用:1]
[12]	陆翌, 王朝亮, 彭茂兰, 等. 一种模块化多电平换流器的子模块优化均压方法[J]. 电力系统自动化, 2014, 38(3): 52-58. LU Yi, WANG Chaoliang, PENG Maolan, et al. Anoptimized method for balancing submodule voltages in modular multilevel converters[J]. Automation of Electric Power Systems, 2014, 38(3): 52-58. (in Chinese) [本文引用:1]
[13]	宋平岗, 江浪, 李云丰, 等. MMC电容电压排序优化算法研究[J]. 工矿自动化, 2014, 40(6): 64-67. SONG Pinggang, JIANG Lang, LI Yunfeng, et al. Research of optimized sorting algorithm of capacitor voltage for MMC[J]. Industry and Mine Automation, 2014, 40(6): 64-67. (in Chinese) [本文引用:1]
[14]	喻锋, 王西田, 林卫星, 等. 一种快速的模块化多电平换流器电压均衡控制策略[J]. 中国电机工程学报, 2015, 35(4): 929-934. YU Feng, WANG Xitian, LIN Weixing, et al. A fast voltage balancing control method for modular multilevel converter[J] Proceedings of the CSEE, 2015, 35(4): 929-934. (in Chinese) [本文引用:1]
[15]	TU Q, XU Z. Impact of sampling frequency on harmonic distortion for modular multilevel converter[J]. IEEE Transactions on Power Delivery, 2011, 26(1): 298-306. [本文引用:2]
[16]	张建坡, 赵成勇, 孙海峰. 基于改进拓扑的MMC-HVDC控制策略仿真[J]. 中国电机工程学报, 2015, 35(5): 1032-1040. ZHANG Jianpo, ZHAO Chengyong, SUN Haifeng. Simulations of control strategies in MMC-HVDC with an improved topology[J]. Proceedings of the CSEE, 2015, 35(5): 1032-1040. (in Chinese) [本文引用:]

2001

0.0

... 模块化多电平变换器(Modular Multilevel Converter, MMC) ,在2001年由文献[1]R ...

2014

0.0

马为民, 吴方劼, 杨一鸣, 等. 柔性直流输电技术的现状及应用前景分析[J]. 高电压技术, 2014, 40(8): 2429-2439.

Weimin

, WU

Fangjie

, YANG

Yiming

, et al. Flexible HVDC transmission technology’s today and tomorrow[J]. High Voltage Engineering, 2014, 40(8): 2429-2439. (in Chinese)

柔性直流输电技术发展至今已经逐步走向成熟,尤其是在欧美地区,已经建成了数十条不同技术路线的柔性直流输电工程,积累了大量的工程经验。而在我国,该技术多年来一直处于理论研究阶段,最近几年才刚刚开始大量兴建示范工程。为给我国柔性直流技术的普及和工程应用提供参考,总结了国内外柔性直流输电的典型工程及技术应用现状。梳理了柔性直流输电的原理、结构和技术特点,系统总结了该技术的演化发展和工程应用经验,分析了柔性直流特有的独立控制有功无功功率,无换相失败问题等优点,提出了受电压源型换流器元件制造水平及其拓扑结构的限制导致柔性直流输送容量小、成本高、故障承受能力较弱等问题。结合我国能源发展战略和电网发展中遇到的问题,对柔性直流输电技术的应用领域以及未来电网的发展方向提出了一些具有积极意义的设想和建议。

... MMC解决了变换器对柔性直流输电的容量限制,在高压直流输电领域具有良好的应用前景^[2] ...

2011

0.0

孙浩, 杨晓峰, 支刚, 等. CPS-SPWM在模块组合多电平变换器中的应用[J]. 北京交通大学学报, 2011, 35(5): 131-136.

SUN

Hao

, YANG

Xiaofeng

, ZHI

Gang

, et al. Application of carrier phase-shifted SPWM in the modular multilevel converter[J]. Journal of Beijing Jiaotong University, 2011, 35(5): 131-136. (in Chinese)

模块组合多电平变换器(MMC)是一种新的拓扑结构,MMC的输出波形为多电平,有效降低了开关器件的物理开关频率和开关损耗;MMC所特有的模块化结构使其设计灵活,利于普及.本文分析了MMC的结构和工作原理,研究了载波移相脉宽调制技术(Carrier Phase-Shifted SP-WM,CPS-SPWM)在MMC中的应用特点,在此基础上提出了CPS-SPWM在MMC中的具体实现方法,仿真结果表明基于CPS-SPWM的MMC具有较大的传输带宽和较高的等效开关频率,有效抑制和消除了低次谐波,CPS-SPWM是一种适合于MMC的调制技术.

... 国内外的研究人员针对MMC的相关问题展开了深入的研究^[3,4,5],其中,子模块电压均衡控制是MMC控制中关键技术之一^[6,7,8] ...

2016

0.0

... 国内外的研究人员针对MMC的相关问题展开了深入的研究^[3,4,5],其中,子模块电压均衡控制是MMC控制中关键技术之一^[6,7,8] ...

2014

0.0

... 国内外的研究人员针对MMC的相关问题展开了深入的研究^[3,4,5],其中,子模块电压均衡控制是MMC控制中关键技术之一^[6,7,8] ...

2012

0.0

李笑倩, 宋强, 刘文华, 等. 采用载波移相调制的模块化多电平换流器电容电压平衡控制[J]. 中国电机工程学报, 2012, 32(9): 49-55.

Xiaoqian

, SONG

Qiang

, LIU

Wenhua

, et al. Capacitor voltage balancing control by using carrier phase-shift modulation of modular multilevel converters[J]. Proceedings of the CSEE, 2012, 32(9): 49-55. (in Chinese)

The aim of this paper was to investigate the application of carrier phase-shift modulation (CPSM) to the apparatus-level controller of modular multilevel converters (MMC), and to propose a relevant capacitor voltage balancing control strategy. Firstly, the paper designed CPSM strategy of an arm and deduced constraints of maintaining the output voltage of an arm. Secondly, the capacitor voltage control principle was theoretically analyzed and the natural energy balancing state of an arm was revealed. Furthermore, additional balancing control strategy was proposed. Experimental results on a 10 kVA laboratory prototype verify the validity of the proposed control method under both steady and dynamic states. The additional balancing control strategy combined with CPSM can guarantee definite switching frequency without costing extra switching loss, and can avoid large calculation efforts.

针对模块化多电平换流器(modular multilevel converter，MMC)的底层控制策略，研究载波移相调制(carrier phase-shift modulation，CPSM)方法及相应的直流电容电压平衡控制策略。首先，以桥臂为单位设计CPSM策略，推导出保证桥臂输出特性不变的约束条件；其次，从理论上分析控制子模块直流电容电压的原理，揭示出桥臂的能量自然平衡状态，进一步提出电容电压的附加平衡控制。在10 kVA实验室样机上进行的稳态和动态实验，验证了所提控制策略的有效性。CPSM结合电容电压附加平衡控制方法，可以使各子模块的开关频率确定，不引起额外的开关损耗，并能够避免计算量过大的问题。

... 国内外的研究人员针对MMC的相关问题展开了深入的研究^[3,4,5],其中,子模块电压均衡控制是MMC控制中关键技术之一^[6,7,8] ...

2015

0.0

... 国内外的研究人员针对MMC的相关问题展开了深入的研究^[3,4,5],其中,子模块电压均衡控制是MMC控制中关键技术之一^[6,7,8] ...

2013

0.0

杨晓峰, 林智钦, 郑琼林, 等. 模块组合多电平变换器的研究综述[J]. 中国电机工程学报, 2013, 33(6): 1-14.

YANG

Xiaofeng

, LIN

Zhiqin

, ZHENG Trillion

, et al. A review of modular multilevel converters[J]. Proceedings of the CSEE, 2013, 33(6): 1-14. (in Chinese)

Modular multilevel converter (MMC), featured with highly modular structure, can easily be extended to high-level, thus leading to low voltage steps and low generation of EMI problems, etc. The operation principles and the technical characteristics of MMC were firstly introduced and summarized. The latest research topics, especially the pulse modulation techniques, dc voltage control, pre-charging control, circulating current and harmonics issues, mathematical modeling, the main circuit parameter design, fault protection, as well as its engineering application status such as electric power drive, power quality conditioning were reviewed in detail. Moreover, the future key issues to be solved urgently were also pointed. It is shown that MMC has good application prospect in future medium- or high- voltage high power applications, especially be one of candidates for HVDC system application.

模块组合多电平变换器(modular multilevel converter，MMC)具有高度模块化、易于扩展、输出电压波形好等特点，尤其适用于中高压大功率系统应用。首先介绍MMC的电路拓扑和工作原理，总结MMC的主要技术特点；然后分别回顾MMC在脉冲调制、直流电压控制、预充电、环流、谐波、数学模型、主电路参数设计、故障保护等关键问题的最新研究进展，以及其在电力传动、电能质量问题治理领域的工程应用现状，在此基础上指出MMC今后亟待研究的关键问题。相关研究结果表明，MMC在电力系统中有广泛的应用前景，是未来中高压大功率系统，尤其是高压输电技术的重要发展方向。

... 国内外的研究人员针对MMC的相关问题展开了深入的研究^[3,4,5],其中,子模块电压均衡控制是MMC控制中关键技术之一^[6,7,8] ...

2011

0.0

屠卿瑞, 徐政, 郑翔, 等. 一种优化的模块化多电平换流器电压均衡控制方法[J]. 电工技术学报, 2011, 26(5): 15-20.

Qingrui

, XU

Zheng

, ZHENG

Xiang

, et al. An optimized voltage balancing method for modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2011, 26(5): 15-20. (in Chinese)

... 为了降低开关频率,文献[9]提出了一种优化的均压方法,通过存储子模块投切状态,使其尽可能保持原有状态,有效地降低了开关频率 ...

2014

0.0

武晓堃, 王奎, 万磊, 等. 模块化多电平变换器三种调制策略及电压平衡控制仿真与对比研究[J]. 电工电能新技术, 2014, 33(12): 4-9.

Xiaokun

, WANG

Kui

, WAN

Lei

, et al. Simulation and comparative study of three modulation strategies and voltage balance control in modular multilevel converter[J]. Advanced Technology of Electrical Engineering and Energy, 2014, 33(12): 4-9. (in Chinese)

模块化多电平变换器作为一种新型的多电平拓扑,因为适用于电压源换流型直流输电场合而得到了广泛研究。本文介绍了模块化多电平变换器的拓扑结构和工作原理,并对常用于模块化多电平变换器拓扑的载波移相、最近电平逼近和载波层叠调制策略以及相应的电容电压平衡算法进行了分析,并在PSCAD/EMTDC下搭建了31电平的模块化多电平变换器仿真模型,分别实现了三种调制策略及其电容电压平衡算法,比较了不同调制策略在电压谐波、电容电压平衡、开关频率等方面的表现,并给出了不同调制策略的特点。

... 文献[10]通过限制排序次数,只在切入的子模块数发生变化时,才对电容电压进行排序,虽然能够降低开关频率,但受子模块数量的影响实际应用效果不佳 ...

2011

0.0

管敏渊, 徐政. MMC型VSC-HVDC系统电容电压的优化平衡控制[J]. 中国电机工程学报, 2011, 31(12): 9-14.

GUAN

Minyuan

, XU

Zheng

. Optimized capacitor voltage balancing control for modular multilevel converter based VSC-HVDC system[J]. Proceedings of the CSEE, 2011, 31(12): 9-14. (in Chinese)

This paper investigated the capacitor voltage balancing problem of the modular multilevel converter (MMC) and the charge and discharge process of sub-module capacitors. The requirement to reduce the switching frequency of power electronic devices is not satisfied in the conventional capacitor voltage balancing control, since it results in high switching losses. To solve this problem, an optimized capacitor voltage balancing control for MMC based VSC-HVDC transmission system was proposed. The optimized voltage balancing control focuses on the sub-modules whose capacitor voltage exceeds the limits, while the switching states of the other sub-modules are maintained to some degrees by employing the maintaining factor. Therefore, the switching frequency of the power electronic device is reduced. The performance of the optimized capacitor voltage balancing control was evaluated with a time-domain simulation in PSCAD/EMTDC. The simulation results show that the optimized voltage balancing control, compared with the conventional one, can more significantly reduce the switching frequency of power device, without noticeablly increasing the capacitor voltage ripples.

介绍模块化多电平换流器(modular multilevel converter，MMC)电容电压平衡的原理以及子模块(sub-module，SM)电容的充放电过程。指出传统的电容电压平衡控制下，子模块投切较频繁，器件开关频率较高，会造成较大的开关损耗。针对传统方法的问题，提出一种适合MMC型直流输电系统的电容电压优化平衡控制策略，将平衡控制的重点放在电容电压越限的子模块上。对电容电压未越限的子模块，优化策略通过引入保持因子使具有一定的保持原来投切状态的能力，以降低开关器件的开关频率。使用PSCAD/EMTDC对优化控制策略进行仿真，结果表明优化平衡控制策略与传统方法相比，可以在基本不增加电容电压波动的前提下，显著降低器件的开关频率。

... 文献[11]提出了保持因子法,通过保持因子稳固子模块的排序位置,使各子模块具有一定保持原来投切状态的能力,一定程度上降低开关器件的开关频率 ...

2014

0.0

陆翌, 王朝亮, 彭茂兰, 等. 一种模块化多电平换流器的子模块优化均压方法[J]. 电力系统自动化, 2014, 38(3): 52-58.

, WANG

Chaoliang

, PENG

Maolan

, et al. Anoptimized method for balancing submodule voltages in modular multilevel converters[J]. Automation of Electric Power Systems, 2014, 38(3): 52-58. (in Chinese)

The sub-module's（SM's）capacitor voltage balancing problem of modular multilevel converters（MMCs）is one of the technical difficulties demanding prompt solution in the MMC engineering application.In contrast to the traditional voltage balancing method which uses the sorting results of SM capacitor voltages according to the direction of the arm current，this paper proposes an improved and optimized method by introducing the double holding factor to reduce the switching frequency and losses.Meanwhile，the voltage balancing strategy of packet sorting is adopted in the proposed method to maintain the relative balance of energy between the SMs by introducing the energy balancing factors on the premise of ensuring normal operation of MMC.The optimized voltage balancing method has realized reduction of the sorting operand and improvement of the capacitor voltage sorting speed.The model of MMC with ten SMs is realized by PSCAD/EMTDC，with both correctness and effectiveness of the proposed method verified by simulation results.

模块化多电平换流器（MMC）的子模块（SM）电容电压均衡问题是MMC工程应用急需解决的难点之一。文中针对采用电容电压进行排序，根据电流方向触发导通的传统电压均衡方法进行了改进和优化，引入了双保持因子，降低SM的开关频率，以减小开关损耗。同时，还通过引入能量均衡因子，使SM间的能量保持相对平衡，在保证换流器正常运行的前提下，对桥臂SM采用分组排序的均压策略，从而达到减小排序运算量，提高SM电容电压排序速度的效果。最后，通过在PSCAD/EMTDC下搭建11电平的MMC仿真模型，对所提出的方法进行了验证，仿真结果证明了所提出的优化均压方法的正确性和有效性。

... 文献[12]采用双保持因子法和分组排序法,既降低了开关频率又提高了排序速度 ...

2014

0.0

宋平岗, 江浪, 李云丰, 等. MMC电容电压排序优化算法研究[J]. 工矿自动化, 2014, 40(6): 64-67.

SONG

Pinggang

, JIANG

Lang

, LI

Yunfeng

, et al. Research of optimized sorting algorithm of capacitor voltage for MMC[J]. Industry and Mine Automation, 2014, 40(6): 64-67. (in Chinese)

根据模块化多电平换流器的运行原理,研究了传统电容电压排序算法导致器件开关频率增大的根本原因;为降低器件的开关频率,提高系统运行效率,提出了一种电容电压排序优化算法.该算法对传统排序算法进行了优化改进,给定3个电压参考值,将已投入的子模块电容电压值与参考值进行比较,判断是否继续保持投入状态.在Matlab中搭建了每相60个子模块的MMC电容电压排序优化算法仿真模型,仿真结果表明,该算法能显著降低功率器件的开关频率,减小换流器的功率耗损.

... 文献[13]通过设置触发条件在传统排序法和优化的排序算法之间进行选择,降低开关频率的程度有限 ...

2015

0.0

喻锋, 王西田, 林卫星, 等. 一种快速的模块化多电平换流器电压均衡控制策略[J]. 中国电机工程学报, 2015, 35(4): 929-934.

Feng

, WANG

Xitian

, LIN

Weixing

, et al. A fast voltage balancing control method for modular multilevel converter[J] Proceedings of the CSEE, 2015, 35(4): 929-934. (in Chinese)

Excessive computation was required in the controller of MMC if typical voltage balancing control based on voltage sorting was adopted. A new voltage balancing control method without sorting was presented in this paper. The number of on-state SMs of the previous and the present control cycle were compared and the deviation between capacitor voltages and their average value in bounds was detected to determine whether to recalculate the trigger pulse. The average voltage was selected as reference value, the sub module whose capacitor voltage was lower than the reference value should be switched on prior in charging status, the sub module whose the capacitor voltage was upper than the reference value should be switched on prior in a state of discharge. A MMC model was set up on the PSCAD/EMTDC, the effectiveness of the design control method was verified. The results show that this voltage balancing method can be realized effectively under low frequency.

模块化多电平换流器(modular multilevel converter,MMC)传统的电压均衡控制需要对电容电压排序,占用了大量计算资源。设计了一种无需排序的均衡控制策略。该策略通过比较前后控制周期中投入子模块的个数以及判断各桥臂子模块的电容电压与其平均值的偏差是否越界,来决定是否重新计算触发脉冲。选取桥臂电容电压的平均值作为基准值,各子模块由其电容电压与该基准值比较来确认投入与否：当桥臂处于充电状态时,优先投入低于基准值的子模块;当桥臂处于放电状态时,优先投入高于基准值的子模块。在PSCAD/EMTDC平台上搭建了MMC模型,对设计的均衡控制策略的有效性进行了验证。结果表明该策略可以在较低频率下实现电容电压的均衡控制。

... 文献[14]通过比较前后控制周期中投入子模块的个数及判断各桥臂子模块的电容电压与其平均值的偏差是否越界,来决定是否重新计算触发脉冲,提出了一种无需排序的均衡控制策略 ...

2011

0.0

... 采样频率过低,可能会使输出电压丢失电平、增加谐波含量^[15] ...

... 根据文献[15]采用传统的恒频排序法时,采样频率应满足: f_c#cod#x02265 ...

2015