引用本文
闫亚光, 杨庆山. 高速列车隧道内会车时气动舒适性研究[J]. 北京交通大学学报, 2017,41(1): 56-61.
YAN Yaguang, YANG Qingshan. Study on aerodynamic comfort of high-speed trains passing each other through a tunnel[J]. JOURNAL OF BEIJING JIAOTONG UNIVERSITY, 2017,41(1): 56-61.
Doi:10.11860/j.issn.1673-0291.2017.01.009  
Permissions
Copyright©2017, 北京交通大学学报编辑部
北京交通大学学报编辑部 所有
高速列车隧道内会车时气动舒适性研究
闫亚光1,2, 杨庆山1
1.北京交通大学 土木建筑工程学院,北京 100044
2.河北工程大学 土木工程学院,河北 邯郸 056038

第一作者:闫亚光(1978—),男,河北永年人,讲师,博士生.研究方向为隧道空气动力学.email:09115283@bjtu.edu.cn

收稿日期: 2016-03-20
基金: 国家自然科学基金重大研究计划(91215302)
摘要

基于N-S方程及k-ε两方程紊流模型,采用有限元法对2列高速列车在隧道内交会时引起的车内压力变化及各参数对乘坐舒适性的影响进行了仿真分析.研究结果表明:2列高速列车在隧道内会车时的瞬变压力值与列车会车的地点、列车长度、列车速度及列车的密封指数均有关系,同车长、车速、密封指数的情况下,会车在隧道中部时瞬变压力变化值最大;同隧长、车速、密封指数的情况下,会车于相同地点时,较长车长的瞬变压力最大变化值要高于较短车长的;当列车的密封指数大于15 s时,各种计算工况均能满足列车内瞬变压力容许值1.25 kPa/3 s的评价标准.

关键词: 高速列车; 隧道工程; 会车; 空气动力学; 舒适性; 数值计算
中图分类号:U451.3;U271;O355 文献标志码:A
Study on aerodynamic comfort of high-speed trains passing each other through a tunnel
YAN Yaguang1,2, YANG Qingshan1
1.School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China
2.School of Civil Engineering, Hebei University of Engineering, Handan Hebei 056038, China
Fund:National Natural Science Foundation of China(91215302)
Abstract

Based on N-S equation and k-ε two equation turbulence model, simulation analyses are conducted on pressure changes inside trains and influences of different parameters on the riding comfort when two high-speed trains passing each other through a tunnel by using finite element method. The results show that the transient pressure inside trains is influenced by the place of trains passing each other, the length of trains, the speed of trains and the sealing index. The maximum transient pressure appears when two trains passing each other in the center of the tunnel when the length of trains, the speed of trains and the sealing index are the same. And compared to the transient pressure of trains with shorter length, that of trains with longer length is larger when the place of trains passing each other, the speed of trains and the sealing index stay the same. The transient pressure inside trains can satisfy the evaluation standard of 1.25kPa/3s under various operating conditions in this paper when the sealing index is higher than 15s.

Keyword: high-speed train; tunnel engineering; trains passing each other; aerodynamic; comfort; numerical simulation

高速列车在隧道内行驶会引起隧道内的气流受到挤压而发生强烈运动, 产生的气动效应(如瞬变压力、微气压波、气动噪声等)会对行车安全和乘坐舒适性产生严重的影响[1, 2, 3].当高速列车在隧道内会车时, 这种压力瞬变会急剧增大, 在列车上产生附加瞬变荷载, 使列车瞬态横摆过大, 横向振动加剧, 影响车体的结构强度, 甚至使车窗玻璃破碎, 气密性不佳的车辆会使车内乘客和乘务人员出现耳鸣、耳痛和呕吐等不舒适感, 严重时会对乘客内耳造成损伤.同时, 过大的压力瞬变还会对隧道洞口周围的环境造成严重干扰, 影响人们的生产和生活[4].这些隧道空气动力学问题会影响高铁的运行条件, 因此亟待解决.

国内外不少学者对高速列车空气动力学效应进行研究, 并取得了一定的成果.文献[5, 6]对高速列车在明线上交会进行了数值模拟, 研究了交会过程中产生的气动压力波引起的强度、运行稳定性、轮轨磨损和安全等明线会车气动效应, 但明线上列车交会产生的气动效应远小于隧道内交会的情况.文献[7, 8, 9]采用一维计算模型研究了高速列车隧道内交会时产生的压力波.而列车交会所引起的隧道内压力波动实为复杂的三维气动流场, 采用三维计算模型应该更为合理.文献[10, 11, 12]采用三维流动模型对高速列车在隧道内交会的全过程进行了数值模拟, 研究了列车交会过程中隧道断面的压力波动、流速变化和压力波的形成过程, 但未对车内的压力变化进行深入研究.高速列车在隧道内交会引起的车内压力变化也是三维流场, 而且司乘人员的主要活动空间在车内, 因此, 有必要对隧道会车时车内的压力变化进行深入地分析, 研究车内气动环境的舒适性.

本文作者基于三维、非稳态、黏性N-S方程及k-ε 两方程紊流模型, 以京沪高速铁路的中长隧道为研究对象, 采用计算流体力学的数值计算方法对隧道内高速列车交会引起的车内压力变化进行仿真模拟, 分析压力变化规律, 研究乘坐舒适性, 为车辆及隧道的设计提供参考.

1 舒适性评价标准与车辆密封性能

高速列车通过隧道时, 车内司乘人员的舒适性与隧道内容许的瞬变压力值有关.容许的瞬变压力值是指在变化的压力波动作用下, 测试人群中大多数人能够承受的压力波动容许值.欧洲铁路研究所(ERRI)和国际铁路联盟(UIC)都已经给出了相应的标准, 我国也制定了相关标准[13].

1.1 ERRI标准

ERRI分别从医学和车内司乘人员舒适感2个角度制定了瞬变压力容许值.从医学上影响健康的角度所制定的标准为列车在隧道内任何时候压力变动都不超过10 kPa, 从司乘人员舒适感的角度所制定的标准如表1所示.ERRI标准对瞬变压力的限制较为宽松, 各国的标准均高于该标准.

表1 ERRI密封列车内基本舒适度标准 Tab.1 Basic comfort standard in the sealed train formulated by ERRI
1.2 UIC标准

国际铁路联盟(UIC)采用1 s、3 s和10 s最大容许瞬变压力变化作为评价车内舒适性的标准, 如表2所示.比较表1和表2可见, ERRI允许的最大容许瞬变压力变化值基本上是UIC允许值的2倍.

表2 UIC密封列车内基本舒适度标准 Tab.2 Basic comfort standard in the sealed train formulated by UIC
1.3 国内标准

文献[13]对我国高速列车通过隧道时车内舒适度的控制标准规定如下:当线路中隧道所占比例大于25%或每h通过的隧道大于4座时, 单线隧道允许的最大瞬变压力宜为0.80 kPa/3 s, 双线隧道宜为1.25 kPa/3 s.

综上可见, ERRI标准的限制较为宽松, UIC标准最为严格, 而国内的规定与UIC标准比较接近.考虑到我国高铁隧道断面积较日本、法国和德国的要大, 舒适度标准可以适当放宽一些.本文研究的京沪高铁隧道为双线隧道, 隧道断面积为100 m2, 因此, 本文以国内标准作为参照.

1.4 车辆密封性能

车辆密封性能直接影响车内的气动舒适性, 提高车辆的气密性能, 可有效缓解隧道内会车压力波动对车内司乘人员舒适性的影响, 但同时也会显著增加车辆的制造成本和维护难度.通常使用密封指数来衡量车辆的气密性能.密封指数τ 为一个具有时间量纲的常数, 即

τ=tlnpi-pofpi-po0(1)

式中:t为车辆内压力泄漏的时间; pi为车内压力; po为车外压力; pi-po0为初始车内外压差; pi-pof为泄漏后车内外压差.

对于高速列车(速度200 km/h及以上), 要求车辆内部的压力从3.60 kPa降低到1.35 kPa时, 其密封指数τ ≥ 15 s.本文以CRH3车型为计算列车模型, 车辆气密性为车内压力从4 kPa降到1 kPa的泄漏时间大于40 s, 密封指数以15 s为基准.

2 数值模拟方法

本文选用有限体积法, 利用滑移网格技术对高速列车隧道内交会情况进行数值计算, 并用模型试验结果验证所建数值模型的可靠性.

2.1 控制方程

列车在隧道内交会引发的三维气动流场可采用连续方程、N-S方程、能量方程和k-ε 两方程紊流模型描述如下[14]:

连续方程

∂ρ∂t+divρV=0(2)

N-S方程

∂ρvx∂t+divρVvx-μgradvx=-∂p∂x+divμ∂V∂x(3)∂ρvy∂t+divρVvy-μgradvy=-∂p∂y+divμ∂V∂y(4)∂ρvz∂t+divρVvz-μgradvz=-∂p∂z+divμ∂V∂z(5)

能量方程

∂ρT∂t+divρVT-μPr+μtσtgradT=∂p∂T(6)

k方程

∂ρκ∂t+divρVκ-μσκgradκ=G-ρε(7)

ε 方程

∂ρε∂t+divρVκ-μσεgradε=εκC1G-C2ρε(8)

状态方程

p=ρRT(9)

式中:ρ 为气体密度; V为气体的速度矢量; p为气体压力; vx、vy、vz为气体速度矢量V在x、y、z坐标轴方向的分量; T为温度; κ 为紊流动能; ε 为紊流动能耗散率; G为耗散函数; μ 为气体的黏度系数; μ t为紊流黏度; Pr为气体比热容; σ t为紊流普朗特数; σ κ 、σ ε 为经验常数, 分别取1.0和1.3; C1、C2为经验常数, 分别取1.44和1.92.

2.2 计算模型

高速列车隧道内会车是一种车隧相对运动问题, 当列车在隧道内会车时, 2列交会列车的计算域边界分别与隧道计算区域边界发生瞬态变化, 可以采用滑移网格技术进行数值模拟[15].滑移网格技术可先根据计算域的实际情况将其划分成不同等级的子区域, 并形成子区域边界, 通过邻接区域网格的线性插值实现发生相对运动的子区域之间物理参数的转换, 各子区域之间交接面的网格点并不一定完全重合.隧内相向运动的2列列车产生的气动压力场可采用这种方法模拟.各级子区域可单独划分网格, 几何形状规则的子区域(如车身、隧道)可划分为六面体网格, 几何形状不规则的子区域(如列车头部、尾部)可划分为四面体网格.图1为列车及隧道计算模型示意图.

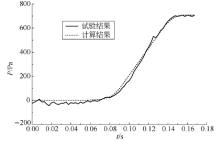
图1 列车及隧道的计算模型Fig.1 Calculation model of the train and the tunnel

2.3 计算模型的验证

为验证计算模型的正确性, 与文献[16]中模型试验数据进行对比分析.试验模型隧道长28 m, 隧道横断面积0.258 m2; 试验采用的模型列车为CRH3动车组, 采用2车编组(流线型头车+流线型尾车), 总车长2.92 m, 车速55.98 m/s.试验模型的线性缩尺比例1/17.6, 测点距离隧道入口约14.2 m.本文以此为条件建立模型, 计算隧道内初始压缩波P, 并与模型试验结果对比.图2为试验结果和本文计算值的对比图.

图2 计算结果与实验结果对比Fig.2 Comparison between calculation results and experimental results

从图2可见, 本文计算的初始压缩波曲线与试验模型的结果吻合较好, 因此可以采用该计算模型进行高速列车隧道内会车的计算研究.

3 计算结果及其分析

京沪高铁北京至徐州段正线隧道一共有9座, 主要以中长隧道为主.因此本文选取1 km长的中长隧道为研究对象, 采用200 m(单车)和400 m(重联)2组CRH3型列车分别以300 km/h、350 km/h、380 km/h的车速在隧道中部、隧道入口1/3处, 以等长、等速的方式会车时产生的复杂压力场进行数值模拟, 列车密封指数τ 分别取0 s、5 s、10 s、15 s、20 s、25 s、40 s, 对车内压力变化进行分析, 以确定其是否满足舒适度标准控制要求.

3.1 200 m长列车隧道中部会车

图3为2列200 m长列车等速会车于隧道中部时, 车头、车尾内3 s的压力变化最大值随密封指数的变化规律, 可见列车头部、尾部车内瞬变压力变化

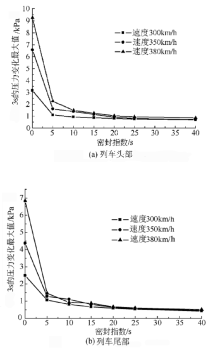图3 2列200 m长列车在隧道中部会车Fig.3 Two trains with the length of 200 m passing each other in the center of the tunnel

最大值随列车密封指数的增大而降低, 在车速和密封指数相同的情况下列车头部瞬变压力变化最大值要大于尾部.

3.2 200 m长列车隧道入口1/3处会车

图4为2列200 m长列车等速会车于隧道入口1/3处时车头、车尾内3 s的压力变化最大值随密封指数的变化规律.

图4 2列200 m长列车在隧道入口1/3处会车Fig.4 Two trains with the length of 200 m passing each other in the position of 1/3 length away from tunnel entrance

比较图3和图4可知, 在车长、车速和密封指数相同的情况下, 会车地点不同, 列车头部和尾部车内瞬变压力变化最大值也不同, 会车在隧道中部时较大.由图4可知, 2列200 m长列车等速会车于隧道入口1/3处时, 列车头部和尾部内瞬变压力变化最大值随列车密封指数的增大而逐渐降低, 在车速和密封指数相同的情况下列车头部瞬变压力的变化要大于尾部的.

从舒适度角度来看, 对于车长200 m, 会车于隧道中部和隧道入口1/3处的2列列车, 在列车头部, 3种车速下密封指数大于15 s的瞬变压力变化最大值均满足1.25 kPa/3 s的评价标准; 在列车尾部, 3种车速下密封指数大于10 s的瞬变压力变化最大值均满足1.25 kPa/3 s的评价标准, 司乘人员不会出现不适感.

3.3 400m长列车隧道中部会车

图5为2列400 m长列车等速会车于隧道中部时车头、车尾内3 s的压力变化最大值随密封指数的变化规律.

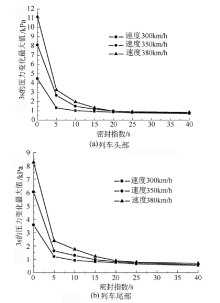图5 2列400 m长列车在隧道中部会车Fig.5 Two trains with the length of 400 m passing each other in the center of the tunnel

比较图3和图5可知, 在车速、密封指数相同的情况下, 会车于隧道中部时, 较长车长的瞬变压力变化最大值要高于较短车长的.由图5可知, 2列400 m长列车等速会车于隧道中部时, 列车头部和尾部车内瞬变压力变化最大值随列车的密封指数的增大而逐渐降低, 在车速和密封指数相同的情况下列车头部瞬变压力的变化要大于尾部的.

3.4 400 m长列车隧道入口1/3处会车

图6为2列400 m长列车等速会车于隧道入口1/3处时车头、车尾内3 s的压力变化最大值随密封指数的变化规律.

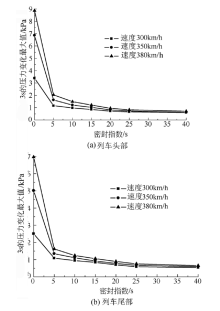图6 2列400 m长列车在隧道入口1/3处等速会车Fig.6 Two trains with the length of 400 m passing each other in the position of 1/3 length away from tunnel entrance

比较图4和图6可知, 在车速和密封指数相同的情况下, 会车于隧道入口1/3处时, 较长车长的瞬变压力变化最大值要高于较短车长的.比较图5和图6可知, 400 m车长工况下, 在车速和密封指数相同, 会车同样是在隧道中部时, 列车头部和尾部车内瞬变压力变化值最大.由图6可知, 2列400 m长列车等速会车于隧道入口1/3处时, 列车头、尾内瞬变压力变化最大值随列车密封指数的增大而逐渐降低, 在车速和密封指数相同的情况下列车头部瞬变压力的变化要大于尾部的.

从舒适度角度来看, 对于车长400 m, 会车隧道中部和隧道入口1/3处的2列列车, 在列车头部, 3种车速下密封指数大于15 s的瞬变压力变化最大值均满足1.25 kPa/3 s的评价标准; 在列车尾部, 会车隧道中部时, 3种车速下密封指数大于15 s的瞬变压力变化最大值均满足1.25 kPa/3 s的评价标准, 会车于隧道入口1/3处时, 3种车速下密封指数大于15 s的瞬变压力变化最大值均满足1.25 kPa/3 s的评价标准.司乘人员不会出现不适感.

4 结论

本文通过对京沪高铁隧道内等速会车进行数值模拟, 分析了列车速度、列车长度、列车密封性及隧道内不同会车地点对列车内不同部位压力变化最大值的影响, 结论总结如下.

1)同车长、车速、密封指数的情况下, 会车地点不同, 列车头、尾内瞬变压力变化最大值也不同, 会车在隧道中部时最大.

2)同会车地点、车速、密封指数的情况下, 较长车长的瞬变压力变化最大值高于较短车长的.

3)2列车长相同的列车等速会车于隧道内时, 列车头、尾内瞬变压力变化最大值随列车速度的增大而增大, 且列车头部瞬变压力变化最大值要大于尾部.

4)2列车长相同的列车等速会车于隧道内时, 列车内瞬变压力变化最大值随列车密封指数的增大而逐渐降低.

5)当列车的密封指数大于15 s时, 本文各种计算工况均能满足国内提出的列车内瞬变压力容许值为1.25 kPa/3 s的评价标准, 列车上的司乘人员均不会出现不适感.

The authors have declared that no competing interests exist.

参考文献
[1] 田红旗. 列车空气动力学[M]. 北京: 中国铁道出版社, 2007: 24-59.
TIAN Hongqi. Train aerodynamics[M]. Beijing: China Railway Press, 2007: 24-59. (in Chinese) [本文引用:1]
[2] 田红旗. 中国高速轨道交通空气动力学研究进展及发展思考[J]. 中国工程科学, 2015, 17(4): 30-41.
TIAN Hongqi. Development of research on aerodynamics of high-speed rails in China[J]. Engineering Sciences, 2015, 17(4): 30-41. (in Chinese) [本文引用:1]
[3] 杨国伟, 魏宇杰, 赵桂林, 等. 高速列车的关键力学问题[J]. 力学进展, 2015, 45(7): 217-460.
YANG Guowei, WEI Yujie, ZHAO Guilin, et al. Research progress on the mechanics of high speed rails[J]. Advances in Mechanics, 2015, 45(7): 217-460. (in Chinese) [本文引用:1]
[4] 梅元贵, 周朝晖, 许建林. 高速铁路隧道空气动力学[M]. 北京: 科学出版社, 2009: 29-39.
MEI Yuangui, ZHOU Chaohui, XU Jianlin. Aerodynamics of high-speed trains in tunnels[M]. Beijing: Science Press, 2009: 29-39. (in Chinese) [本文引用:1]
[5] 李人宪, 刘杰, 戚振宕, 等. 明线会车压力波幅变化规律研究[J]. 机械工程学报, 2011, 47(4): 125-130.
LI Renxian, LIU Jie, QI Zhendang, et al. Air pressure pulse developing regularity of high-speed trains crossing in open air[J]. Journal of Mechanical Engineering, 2011, 47(4): 125-130. (in Chinese) [本文引用:1]
[6] 郗艳红, 毛军, 柳润东, 等. 高速列车明线会车压力波波幅研究[J]. 华南理工大学学报(自然科学版), 2016, 44(3): 118-127.
XI Yanhong, MAO Jun, LIU Rundong, et al. A probe into air pressure pulse amplitude of high-speed trains crossing in open air[J]. Journal of South China University of Technology(Natural Science Edition), 2016, 44(3): 118-127. (in Chinese) [本文引用:1]
[7] WOODS W A, POPE C W. A generalised flow prediction method for the unsteady flow generated by a train in a single-track tunnel[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1981, 7(3): 331-360. [本文引用:1]
[8] VARDY A E, DAYMAN B. Alleviation of tunnel entry pressure transients: 2. theoretical modeling and experimental correlation[C]//3rd International Symposium on Aerodynamics and Ventilation of Vehicle Tunnels. Sheffield, UK, 1979: 363-373. [本文引用:1]
[9] 梅元贵, 赵海恒, 刘应清. 隧道内高速列车会车压力波的数值模拟方法[J]. 兰州铁道学院学报, 1996, 15(1): 1-6.
MEI Yuangui, ZHAO Haiheng, LIU Yingqing. The numerical prediction method of the high speed train crossing pressure waves in a single bore tunnel[J]. Journal of Lanzhou Railway Institute, 1996, 15(1): 1-6. (in Chinese) [本文引用:1]
[10] 梅元贵, 孙建成, 许建林, 等. 高速列车隧道交会压力波特性[J]. 交通运输工程学报, 2015, 15(5): 34-43.
MEI Yuangui, SUN Jiancheng, XU Jianlin, et al. Crossing pressure wave characteristics of high-speed trains in tunnel[J]. Journal of Traffic and Transportation Engineering, 2015, 15(5): 34-43. (in Chinese) [本文引用:1]
[11] 许建林, 孙建成, 梅元贵, 等. 高速列车隧道内交会压力波基本特性数值模拟研究[J]. 振动与冲击, 2016, 35(3): 184-191.
XU Jianlin, SUN Jiancheng, MEI Yuangui, et al. Numerical simulation on crossing pressure wave characteristics of two high-speed trains in tunnel[J]. Journal of Vibration and Shock, 2016, 35(3): 184-191. (in Chinese) [本文引用:1]
[12] 李人宪, 关永久. 高速列车隧道会车压力波动问题[J]. 机械工程学报, 2012, 48(20): 127-134.
LI Renxian, GUAN Yongjiu. Investigation of air pressure pulse when two high-speed trains passing by each other in tunnel[J]. Journal of Mechanical Engineering, 2012, 48(20): 127-134. (in Chinese) [本文引用:1]
[13] 铁路隧道设计施工有关标准补充规定[Z]. 北京: 中华人民共和国铁道部, 2007.
Beijing: Ministry of Railways of the People's Republic ofRailway tunnel design and construction related stand ards supplementary provisions[Z]. Beijing: Ministry of Railways of the People's Republic of China, 2007. (in Chinese) [本文引用:2]
[14] 闫亚光, 杨庆山, 骆建军. 缓冲结构对隧道气动效应减缓效果[J]. 北京交通大学学报, 2013, 37(4): 7-12.
YAN Yaguang, YANG Qingshan, LUO Jianjun. Mitigation result of hoods on aerodynamic effect in tunnel[J]. Journal of Beijing Jiaotong University, 2013, 37(4): 7-12. (in Chinese) [本文引用:1]
[15] 王英学, 高波, 朱丹, 等, 高速铁路隧道空气动力效应控制技术[M]. 北京: 科学出版社, 2012: 46-51.
WANG Yingxue, GAO Bo, ZHU Dan, et al. Aerodynamic control technology of high-speed trains in tunnels[M]. Beijing: Science Press, 2012: 46-51. (in Chinese) [本文引用:1]
[16] 徐向东, 赵文成, 王英学, 等. 高速铁路隧道关键技术研究报告[R]. 武汉: 中铁第四勘测设计院集团有限公司, 2011.
XU Xiangdong, ZHAO Wencheng, WANG Yingxue, et al. Report of key techniques about the high speed railway tunnel[R]. Wuhan: China Railway Siyuan Survey and Design Group Co Ltd, 2011. (in Chinese) [本文引用:1]